螺栓連接結(jié)構(gòu)對(duì)系統(tǒng)動(dòng)力學(xué)特性的影響
李 暢(中國(guó)電子科技集團(tuán)公司第三十八研究所,合肥 230088)
螺栓連接結(jié)構(gòu)對(duì)系統(tǒng)動(dòng)力學(xué)特性的影響
李暢
(中國(guó)電子科技集團(tuán)公司第三十八研究所,合肥230088)
工程實(shí)際中,能否處理好接觸非線性問題是解決零件之間的連接裝配的關(guān)鍵。文中以L形螺栓連接結(jié)構(gòu)為例,理論分析了影響接觸剛度的主要因素,推導(dǎo)得到其計(jì)算公式。通過有限元非線性靜力學(xué)分析方法,計(jì)算施加預(yù)緊力螺栓結(jié)構(gòu)的靜力學(xué)變形,給出接觸面積以及接觸力的大小,并以此結(jié)果為依據(jù),修改模型邊界條件,利用MPC模擬接觸條件,建立結(jié)構(gòu)的動(dòng)力學(xué)模型。分別對(duì)等效模型和一體化分析模型進(jìn)行模態(tài)分析,并將振動(dòng)試驗(yàn)與有限元仿真分析進(jìn)行對(duì)比,得到如下結(jié)論:該等效模型可以用來模擬接觸非線性問題,為以后工程中的類似問題提供了一種有效解決方案。
螺栓連接;有限元分析;非線性;動(dòng)力學(xué)特性
0 引言
目前,有限元分析技術(shù)業(yè)已成熟,利用有限元分析技術(shù)可以對(duì)簡(jiǎn)單零部件或結(jié)構(gòu)件進(jìn)行精確計(jì)算仿真,得到的仿真結(jié)果完全可以用來分析實(shí)際工程問題。但是在許多情況下,需要對(duì)一些機(jī)械系統(tǒng)進(jìn)行結(jié)構(gòu)分析,即利用各種裝配手段,如配合連接、螺栓連接、銷連接、焊接、膠接、嚙合連接等等方式,將大量的零部件和組件等裝配在一起而構(gòu)成的[1]。在對(duì)諸如此類的機(jī)械系統(tǒng)進(jìn)行有限元分析時(shí),能否恰當(dāng)處理零件或組件之間的連接裝配關(guān)系是一直困擾工程技術(shù)人員的關(guān)鍵問題,并已經(jīng)限制了有限元分析技術(shù)的發(fā)展和應(yīng)用。
在工程設(shè)計(jì)中,需要簡(jiǎn)化分析模型才能對(duì)機(jī)械系統(tǒng)的裝配結(jié)構(gòu)進(jìn)行有限元?jiǎng)恿W(xué)仿真分析,一般有以下幾種簡(jiǎn)化方式[2]:一是一體化分析模型方法,忽略零件之間的連接裝配關(guān)系,將機(jī)械系統(tǒng)中的所有零部件看成一個(gè)整體,并假定裝配體之間的連接是剛性連接。這種分析模型的優(yōu)點(diǎn)是數(shù)據(jù)比較簡(jiǎn)單,計(jì)算量小,缺點(diǎn)是完全忽略了裝配結(jié)構(gòu)中的連接剛度和連接阻尼對(duì)系統(tǒng)動(dòng)力學(xué)特性的影響,而且計(jì)算結(jié)果在很大程度上偏離實(shí)際情況,實(shí)際應(yīng)用中參考價(jià)值較小;二是,利用附加面技術(shù)處理結(jié)合面問題的方法。以螺栓連接為例,分析模型不是通過螺栓孔和螺栓來連接,而在兩接觸面之間另外定義一層具有某些特定屬性的附加面,采用調(diào)整該附加面的各種屬性參數(shù)的方式,便可以準(zhǔn)確地模擬出任意復(fù)雜工況下的連接剛度。但是,該方法需要先做振動(dòng)試驗(yàn),然后根據(jù)試驗(yàn)結(jié)果對(duì)附加面的彈性模量、密度等參數(shù)進(jìn)行迭代優(yōu)化,才能較準(zhǔn)確的反應(yīng)試驗(yàn)情況,具有滯后性且應(yīng)用范圍不廣,故不適用于前期結(jié)構(gòu)設(shè)計(jì)階段。
本文以L形螺栓連接結(jié)構(gòu)為例,通過理論計(jì)算,綜合利用接觸非線性問題的有限元仿真分析和模態(tài)分析方法,計(jì)算螺栓連接結(jié)構(gòu)的瞬態(tài)動(dòng)力學(xué)響應(yīng),分析其動(dòng)力學(xué)特性的影響因素,并通過具體的振動(dòng)試驗(yàn)得到反饋,即本文提出的等效模型可以準(zhǔn)確地模擬接觸非線性問題。
1 接觸剛度計(jì)算模型
機(jī)械表面常會(huì)存在很多微凸體,故兩個(gè)粗糙面的接觸問題可以轉(zhuǎn)化為微凸體的接觸問題。為便于研究,將兩粗糙表面的接觸問題簡(jiǎn)化為光滑與粗糙彈性表面相接觸[3]。
假定基準(zhǔn)面與光滑表面間距為d,微凸體波峰分布的概率密度函數(shù)為()zφ,對(duì)于某一微凸體,波峰位于基準(zhǔn)面的間距在z和z+dz之間的概率為()z dzφ。所以,當(dāng)微凸體的高度z大于間距d時(shí),即可判定兩者接觸,其概率為
因此,某一接觸面間相互接觸的微凸體個(gè)數(shù)
m為接觸面上微凸體的總個(gè)數(shù),接觸面積為Ac。其中,位于基準(zhǔn)面的間距在z和z+dz之間的接觸點(diǎn)數(shù)為mφ(z) dz。上述接觸微凸
體與基準(zhǔn)面之間的法向接近量為(z-d),預(yù)期的載荷W為:
將式(1)等式兩邊均除以接觸面積Ac,可以得到載荷pc的表達(dá)式如下:
式中,n=m/Ac,為單位輪廓面積上的微凸體數(shù)。由式(2)能夠看出,載荷pc與接觸表面間距h之間是非線性關(guān)系。但是,微凸體的變形遠(yuǎn)遠(yuǎn)大于波紋的變形,即h值僅在某一值的附近做微小的變動(dòng),可以將非線性關(guān)系簡(jiǎn)化為線性關(guān)系來描述,其中的影響因子即可表述為剛度系數(shù)k。對(duì)式(2)兩端取微分,可得:
將上述各表達(dá)式代入式(3)可得:
經(jīng)式(4)可知?jiǎng)偠认禂?shù)k的計(jì)算公式為:
經(jīng)式(2)可知,在表面特征參數(shù)為已知的情況下,當(dāng)相互接觸的兩物體表面特征屬性一定的前提下,h值只與外作用載荷pc有關(guān),將其代入式(5)中,經(jīng)計(jì)算簡(jiǎn)化可得:
式中,C為相互接觸的兩物體表面特征屬性一定的前提下k中的常數(shù),其大小與外作用載荷的大小有關(guān)。
因此,對(duì)于接觸面積為Ac的整個(gè)接觸面,其總的剛度系數(shù)K為
式中,
Aa為有效作用區(qū)域,即有效接觸區(qū)域表面積,nB為單位理論接觸面積上的波紋分布密度。2
根據(jù)式(10)能夠看出,當(dāng)接觸物體間的各參數(shù)屬性一定的前提下,接觸剛度的大小僅取決于有效作用區(qū)域和外作用力的大小。
2 螺栓連接結(jié)構(gòu)有限元分析
2.1L形螺栓連接結(jié)構(gòu)模型為驗(yàn)證上述理論分析的正確性,對(duì)如圖1所示的L形螺栓連接結(jié)構(gòu)進(jìn)行仿真分析。結(jié)構(gòu)中的兩個(gè)L形梁外形尺寸為長(zhǎng)150mm、寬30mm、厚8mm,材料均采用45鋼。梁1一端固定,另一端與梁2通過3個(gè)M6X30的螺栓連接,梁2另一端為自由狀態(tài),組成一個(gè)螺栓連接結(jié)構(gòu)。在預(yù)緊力矩T的作用下,螺栓頭部和螺母的支撐面壓緊被連接件,給被連接件施加了一定的壓應(yīng)力,此壓應(yīng)力在其作用區(qū)域內(nèi)分布不均,且此作用區(qū)域的覆蓋范圍也很難準(zhǔn)確測(cè)定,所以對(duì)螺栓連接件進(jìn)行精準(zhǔn)地模態(tài)分析是相當(dāng)困難的。在大多數(shù)工程分析中,通常采用圓錐體、圓柱體及球臺(tái)等一些簡(jiǎn)單模型來模擬壓應(yīng)力的作用區(qū)域,并取得較好的分析效果。本文選擇中空?qǐng)A柱體進(jìn)行模擬仿真分析[4]。
2.2基于接觸非線性的螺栓連接結(jié)構(gòu)靜力學(xué)計(jì)算
首 先, 利 用MSC. Patran軟件建立上述螺栓連接結(jié)構(gòu)的仿真分析模型,并對(duì)其進(jìn)行靜力學(xué)分析。為了較為準(zhǔn)確地獲得接觸面積與接觸力的大小,需對(duì)螺栓及連接區(qū)域的模型劃分更為精細(xì),如圖2所示。施加在螺栓上的預(yù)緊力矩T與預(yù)緊力Fp的大小近似表達(dá)式為T ≈1.25μFpd,其中,μ為相互接觸面之間的摩擦系數(shù),通常取為0.2左右,d為螺桿直徑。因此,結(jié)合本例可以計(jì)算得到,當(dāng)預(yù)緊力矩為1N?m時(shí),預(yù)緊力約為888.9N。
圖3所示為施加一定預(yù)緊力的螺栓連接結(jié)構(gòu)的應(yīng)力作用云圖。根據(jù)應(yīng)力云圖,確定出圖中最大應(yīng)力作用區(qū)域范圍,將該區(qū)域簡(jiǎn)化為以螺栓孔中心為圓心,具有一定大小的圓環(huán)形區(qū)域,并規(guī)定此區(qū)域?yàn)閮山佑|面間的等效接觸區(qū)域。
2.3螺栓連接結(jié)構(gòu)的動(dòng)力學(xué)分析
基于上述有限元靜力學(xué)分析結(jié)果,建立螺栓連接結(jié)構(gòu)的有限元?jiǎng)恿W(xué)模型如圖4所示。在上下接觸面孔中心處各建立一個(gè)獨(dú)立結(jié)點(diǎn),然后將上下連接面等效接觸區(qū)域內(nèi)的節(jié)點(diǎn)利用耦合單元節(jié)點(diǎn)(MPC)的方法連接到兩個(gè)獨(dú)立節(jié)點(diǎn)上,在兩個(gè)獨(dú)立節(jié)點(diǎn)之間建立一個(gè)梁?jiǎn)卧靡阅M螺桿的剛度,等效接觸區(qū)域外的節(jié)點(diǎn)不予連接,從而將螺栓連接的接觸非線性問題轉(zhuǎn)化為線性問題。
建立對(duì)比方案以驗(yàn)證等效模型的準(zhǔn)確性和適用性。其一,選取上述等效模型;其二選取一體化模型,即將裝配結(jié)構(gòu)中的所有零件直接合并為一個(gè)一體化整體,用剛性連接等效結(jié)構(gòu)組件之間的連接。對(duì)兩種模型進(jìn)行模態(tài)分析,比較分析結(jié)果,進(jìn)行差異對(duì)比。
分別計(jì)算上述模型在1N?m、5N?m預(yù)緊力矩下的前5階頻率,計(jì)算結(jié)果如表1~2所示。
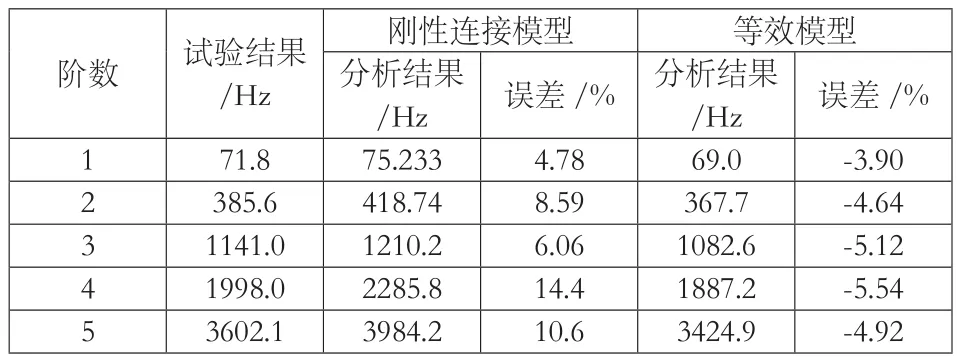
表1 1N?m預(yù)緊力矩作用下結(jié)構(gòu)的前5階頻率
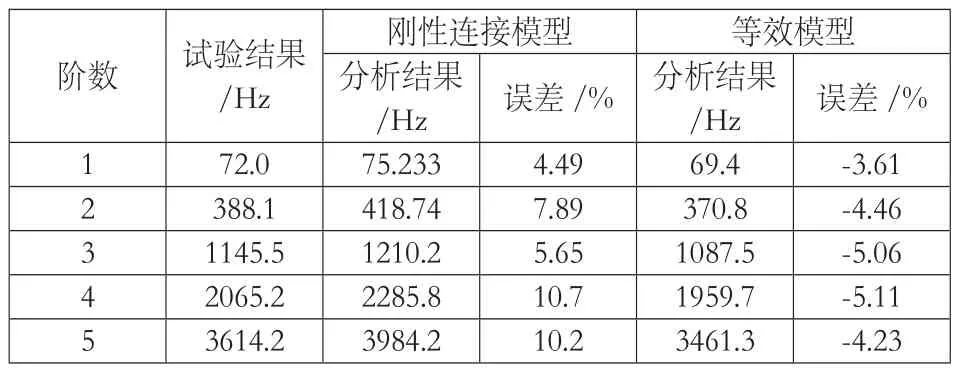
表2 5N?m預(yù)緊力矩作用下結(jié)構(gòu)的前5階頻率
3 振動(dòng)試驗(yàn)
對(duì)上述結(jié)構(gòu)尺寸的L形螺栓連接件進(jìn)行了振動(dòng)試驗(yàn),分別測(cè)得試驗(yàn)件在1N?m 、5N?m預(yù)緊力矩下的前5階固有頻率,并與有限元分析結(jié)果對(duì)比如表1~2所示。
4 結(jié)論
本文從理論上推導(dǎo)了影響接觸剛度的主要因素,導(dǎo)出了其計(jì)算公式,由公式可以導(dǎo)出影響接觸剛度大小的主要因素,當(dāng)接觸物體間的各參數(shù)屬性一定的前提下,接觸剛度的大小僅取決于有效作用區(qū)域和外作用力的大小。連接結(jié)構(gòu)間的螺栓預(yù)緊力越大,即外作用力越大,結(jié)構(gòu)接觸剛度越大,表現(xiàn)出的特性就是結(jié)構(gòu)的固有頻率越高。
本文利用有限元分析軟件MSC.Patan對(duì)L形螺栓連接結(jié)構(gòu)進(jìn)行分析時(shí),采用了以下兩種簡(jiǎn)化模型,一種是忽略接觸的影響,直接合并為一個(gè)整體的剛性模型,另一種是考慮了螺栓預(yù)緊力對(duì)接觸剛度的影響,采用等效接觸區(qū)域的等效模型。以實(shí)際振動(dòng)試驗(yàn)的結(jié)果為基準(zhǔn),通過對(duì)比以上兩種簡(jiǎn)化模型的靜力學(xué)和動(dòng)力學(xué)分析結(jié)果,可以看出剛性模型的分析結(jié)果偏大,且誤差較大,最小誤差為4.49%,最大誤差高達(dá)14.4%,并且螺栓預(yù)緊力的大小對(duì)結(jié)構(gòu)剛度的模擬分析結(jié)果無任何影響。而等效模型的前5階固有頻率更接近實(shí)際試驗(yàn)結(jié)果,最大誤差僅為-5.54%。
綜上所述,本文提出的基于有效作用區(qū)域的等效模型,能夠更加準(zhǔn)確地分析螺栓連接結(jié)構(gòu)對(duì)系統(tǒng)剛度的影響,該等效模型可以用來模擬接觸非線性問題,為以后工程中的類似問題提供了一種更加有效便捷的解決方案。
[1]李成,朱紅紅,鐵瑛等.單搭膠/螺栓混合連接結(jié)構(gòu)的應(yīng)力分布與載荷分配[J].吉林大學(xué)學(xué)報(bào)(工學(xué)版),2013,43(04):933-938.
[2]饒柱石.拉桿組合式特種轉(zhuǎn)子動(dòng)力學(xué)特性及其接觸剛度的研究[D].哈爾濱:哈爾濱工業(yè)大學(xué),1992.
[3]欒宇.航天器結(jié)構(gòu)中螺栓法蘭連接的動(dòng)力學(xué)建模方法研究[D].大連:大連理工大學(xué),2011.
[4]黎定仕,張以都,王鵬.基于結(jié)構(gòu)阻尼的機(jī)械結(jié)合部動(dòng)力學(xué)模型研究[J].振動(dòng)與沖擊,2010,29(08):204-208.
10.16640/j.cnki.37-1222/t.2016.10.010
李暢(1988-),男,安徽金寨人,博士,工程師,研究方向:微系統(tǒng)結(jié)構(gòu)設(shè)計(jì)。

