拉格朗日中值定理在定積分計算中的妙用

劉燈明

(湖南科技大學 數學與計算科學學院，湖南 湘潭 411201)

?

拉格朗日中值定理在定積分計算中的妙用

劉燈明

(湖南科技大學 數學與計算科學學院，湖南 湘潭 411201)

利用定義計算定積分時，若采用常規方法來分割積分區間和選取介點集，會使得積分和式的極限過程十分復雜。通過拉格朗日中值定理巧妙地選取中值點作為介點，可以簡化積分和式的極限過程，從而簡潔地得到計算結果。同時，利用拉格朗日中值定理，也可從另一角度推導出牛頓-萊布尼茨公式，從而將微分學中的微分中值定理和積分學中的微積分基本公式有機地結合起來。

拉格朗日中值定理；定積分計算；牛頓-萊布尼茨公式

拉格朗日中值定理是一元函數微分學中的一個重要內容，它深刻地反映了函數在某區間上的整體性質與函數在該區間上某點處的導數之間的關系。因此，拉格朗日中值定理在《數學分析》課程教學中的應用十分廣泛，比如，通過構造合適的輔助函數，借助拉格朗日中值定理，我們可以方便快捷地證明一些不等式或恒等式、根的存在性問題、復雜級數的斂散性問題及某些復雜函數的極限[1-3]。本文通過具體例子來說明拉格朗日中值定理在定積分教學中的一個巧妙應用。

1　利用拉格朗日中值定理計算定積分

定積分是數學分析課程中除微分學外的另一核心內容。在整個定積分的教學過程中，定積分的計算是讓許多初學者都感到困惑的難點。事實上，計算定積分的主要工具就是定積分的定義和牛頓-萊布尼茨公式。我們知道，若f為區間[a,b]上的可積函數，則對積分區間的任意分割與介點集{ξi}的自由選取都不會影響到積分值。基于此，在利用定積分的定義計算定積分時候，我們都是對[a,b]采取特殊的分割T(通常采取等分積分區間)，并選取特殊的介點集{ξi}(通常取每一小區間的左端點或右端點)來構造積分和，最后再求積分和的極限。

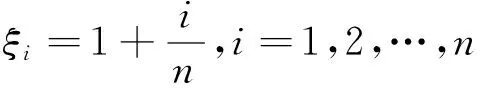
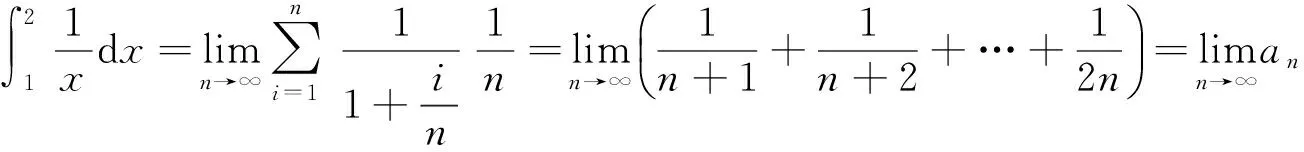
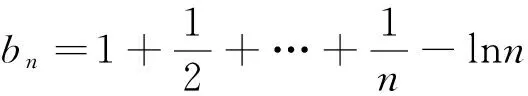
由不等式

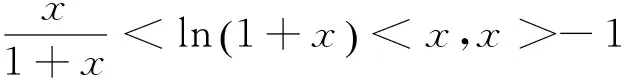
有

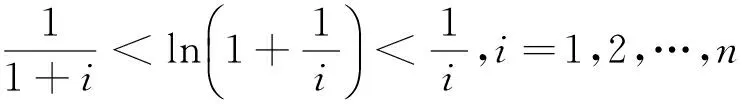
從而有

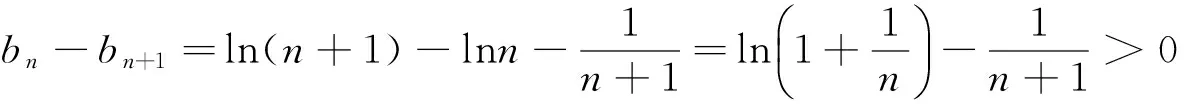
及

另一方面，有

an=b2n-bn+ln2n-lnn=b2n-bn+ln2。

故

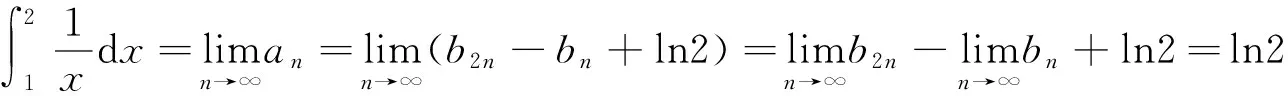
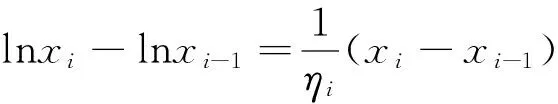
選取介點ξi=ηi，則有

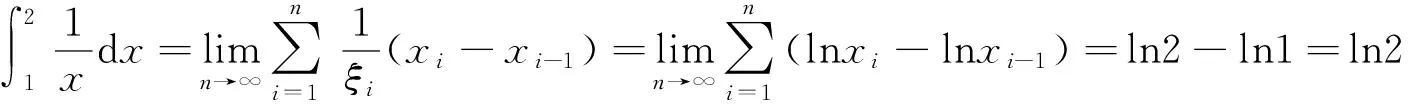
(1)

解法二并沒有具體的給出介點集，而是先對F(x)=lnx在每一小區間[xi-1,xi]上運用拉格朗日中值定理，再選取拉格朗日中值點作為介點。較之解法一，解法二容易理解，且避開了復雜的極限過程，整個計算顯得十分簡潔和方便。

2　結語

若被積函數在積分區間上連續且其原函數容易求出時，可以采取解法二中的處理手法來選擇介點集。事實上，從(1)式可以看出，解法二本質上還是將定積分的計算轉化為計算原函數在積分區間上的增量。故只需將解法二的表述更一般化，就可作為牛頓-萊布尼茨公式教學的一個新的引入。換句話說，從用定義計算定積分出發，利用拉格朗日中值定理，就可以得到一個異于文獻[4-5]的牛頓-萊布尼茨公式的推導。可見，在數學分析課程教學過程中，完全可以將拉格朗日中值定理和定積分有機地結合起來，加深學生對相關內容的理解和掌握。

[1] 石業嬌.談拉格朗日中值定理在高等數學課程教學中的應用[J].常州信息職業技術學院學報，2014(13)：26-28.

[2] 鄭攀，胡學剛，李玲.關于拉格朗日中值定理在證明題中的一些應用[J].科教文匯，2015(6)：59-60.

[3] 裘兆泰，王承國，章仰文.數學分析學習指導[M].北京：科學出版社，2004.

[4] 陳傳璋，金福臨，朱學炎，等.數學分析(上冊)[M].北京：高等教育出版社，2010.

[5] 湯四平，呂勝祥，趙雨清.高等數學(上冊)[M].北京：人民郵電出版社，2015.

(責任校對朱正余)

10.13582/j.cnki.1674-5884.2016.07.014

20160105

2015年湖南科技大學教學研究與改革一般項目(G31515)

劉燈明(1984-)，男，湖南隆回人，講師，博士，主要從事非線性偏微分方程的研究。

G642.0

A

1674-5884(2016)07-0043-02