利用有限域GF(2m)上的三項式構造二元循環碼

張愛仙，馮克勤

（1.西安理工大學數學系，陜西 西安　710048；2.清華大學數學系，北京　100084）

利用有限域GF(2m)上的三項式構造二元循環碼

張愛仙1，馮克勤2

（1.西安理工大學數學系，陜西 西安710048；2.清華大學數學系，北京100084）

循環碼是一類特殊的線性碼，由于循環碼快速的編碼和譯碼算法，它被廣泛應用于消費電子，數據存儲以及通信系統當中.在本文中，利用特征是偶數的有限域上的三項式構造出了兩類二元循環碼，我們不僅可以確定出這兩類循環碼最小距離的下界，而且這兩類循環碼在參數的選取上非常的靈活.關鍵詞：循環碼；三項式；序列；有限域

1　引言

設 q是素數 p的冪.向量空間 GF(q)n的一個線性子空間叫作 q元線性碼.若此子空間是GF(q)n的k-維子空間且極小漢明重量是d，則稱此空間為參數［n，k，d］的q元線性碼.碼長為 n的 q元線性碼 C叫作循環碼，是指若 (c0，c1，...，cn-1)∈C，則它的循環移位(cn-1，c0，c1，...，cn-2)∈C.

把向量(c0，c1，...，cn-1)∈GF(q)n等同于多項式

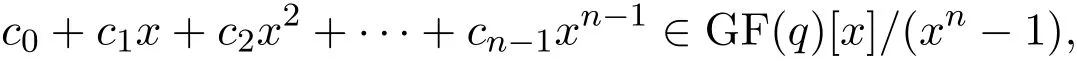
則 GF(q)上碼長為 n的循環碼 C對應于 GF(q)［x］/(xn-1)中的子集.如果C是循環碼當且僅當C在GF(q)［x］/(xn-1)中對應的子集是商環 GF(q)［x］/(xn-1)的一個理想.熟知GF(q)［x］/(xn-1)中每個理想都是主理想.設C=(g(x))，則稱g(x)是循環碼C的生成多項式，h(x)=(xn-1)/g(x)是循環碼C的校驗多項式.關于有限域與糾錯碼的基礎知識讀者可參見［1-3］.

設s∞=(si)∞i=0是GF(q)上周期為n的序列，

設Cs是以如下多項式

為生成多項式的循環碼.

那么一個自然的問題是：用此方法能否構造出性能最優的循環碼？事實表明，只要選取合適的序列s∞，用此方法可以構造出最優或幾乎最優的循環碼，見文獻［4-5］.

設m是正整數，n=2m-1，α是GF(2m)?的生成元.f(x)是GF(2m)上的多項式，定義由f(x)得到的序列s∞，其中

Tr(x)表示由GF(2m)到GF(2)的絕對跡映射.在本文中，通過選取GF(2m)上恰當的三項式f(x)，以(1)式定義的多項式為生成多項式構造出了兩類二元循環碼，我們不僅可以確定出這兩類循環碼最小距離的下界，而且這兩類循環碼在參數的選取上非常的靈活.

2　若干引理

設n=2m-1.包含j模n的2-分圓陪集定義為Cj={j，2j，22j，...，2?j-1j}，

其中?j是使得等式2?jj≡j(mod n)成立的最小正整數.

引理2.1設h是整數，且

則對任意j∈Γ1，

?j是Cj的首元；

??j=m，若m是奇數；?2m/2+1=m/2，若m是偶數.

證明先證明第一個結論.由于陪集首元一定是奇數，對任意j∈Γ1，假設

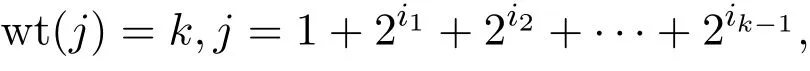
其中

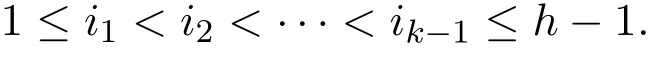
則Cj中所有的奇數為由于當1≤t≤k-1時，it≤m/2，可知j是Cj的首元.

現在證明第二個結論.當j∈Γ1時，?j|m并且j可被(2m-1)/(2?j-1)整除.當m是奇數時，如果?j＜m，則?j≤m/3，從而(2m-1)/(2?j-1)＞22m/3，即證明了j＞22m/3.這是不可能的，因為j＜2(m+1)/2.于是證明了，當m是奇數時，?j=m.類似地，當m是偶數時，如果?j＜m，則?j≤m/2，(2m-1)/(2?j-1)＞2m-?j.很容易可以證明，當j∈Γ1時，j可被(2m-1)/(2?j-1)整除當且僅當j=2m/2+1并且?j=m/2.

對于周期序列，一般來說很難確定出它的線性復雜度以及極小多項式，下面給出文獻［6］中的一個結果.

引理 2.2[6]GF(q)上周期為qn-1的序列s∞可以展開成如下唯一的表達式

其中α是GF(qn)?的生成元，ci∈GF(qn).設I={i|ci/=0}，則s∞的極小多項式為

s∞的線性復雜度是|I|.

其中

證明對任意奇數j，1≤j≤2h-1.設Bj={1≤i≤2h-1：i∈Cj}.由分圓陪集可知，

并且

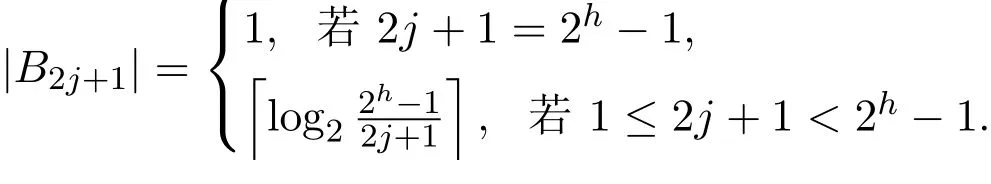
從而

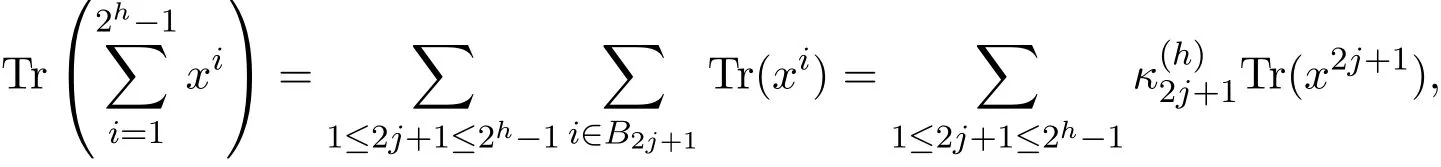
其中

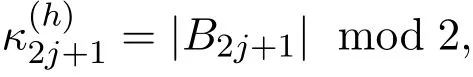
又因為對任意i∈B2j+1，Tr(xi)=Tr(x2j+1)可知第二個等式成立.

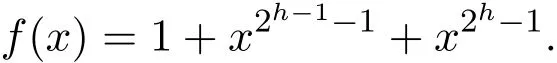
設LC是序列s∞的線性復雜度，則LC(s∞)=m2h-1+N2(m)，其中

序列s∞的極小多項式為

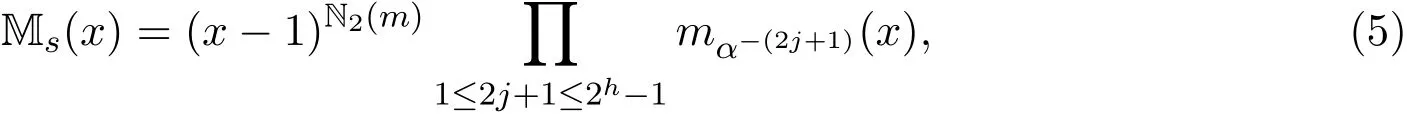
其中mαj(x)是αj的極小多項式.

證明由f(x)的定義及引理2.3可知，

由(4)可知，當

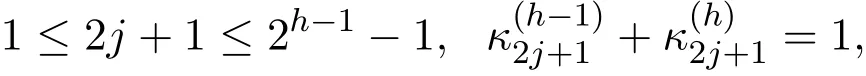
當

于是，上式中最后一個等式成立.

注意到，對任意t≥0，st=Tr(f(1+αt)).由引理2.1，引理2.2以及公式(6)可知序列s∞的線性復雜度和極小多項式.從而引理得證.

3　循環碼的兩類構造

本節用引言中介紹的方法給出循環碼的兩類構造，由定理3.1和3.2可以看出這兩類碼在參數的選取上非常的靈活，對循環碼的編碼和譯碼算法感興趣的讀者可參考文獻［7-10］.

3.1第一類構造

是以

為生成多項式的循環碼.

定理3.1設Cs是由上述序列s∞定義的循環碼，則

(1)Cs的生成多項式為

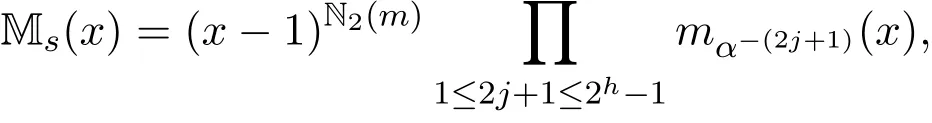
其中mαj(x)是αj的極小多項式.

(2)Cs是參數為［n，n-m2h-1-N2(m)，d］的循環碼，其中，

當m是奇數時，d≥2h+2；當m是偶數時，d≥2h+1.

證明(1)由引理2.4可得到Cs的生成多項式.

(2)由Cs的定義以及引理2.3可知它的維數為n-m2h-1-N2(m).下面證明極小距離d的下界，熟知以Ms(x)為生成多項式生成的循環碼與以Ms(x)的互反多項式為生成多項式生成的循環碼有相同的重量分布，由引理2.4可知，當j∈{1，...，2h}時，αj是Ms(x)的互反多項式的零點.由BCH碼的下界得d≥2h+1.若m是奇數，則Cs是偶重碼，從而可知d≥2h+2.

例3.1設(m，h)=(5，3)，α是GF(2m)?的生成元，α5+α2+1=0.則Cs是以Ms(x)=x21+x20+x19+x18+x17+x16+x15+x13+x12+x10+x8+x7+x4+x2+x+1，為生成多項式，參數為［31，10，12］的最優二元循環碼.

例3.2設(m，h)=(7，3)，α是GF(2m)?的生成元，α7+α+1=0.則Cs是以Ms(x)=x29+x23+x21+x20+x18+x14+x13+x12+x11+x10+x8+x7+x6+x5+x2+1，為生成多項式，參數為［127，98，10］的最優二元循環碼.

3.2第二類構造

設m是大于等于5的奇數，

α是GF(2m)?的生成元，

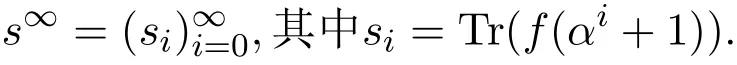
設

是以

為生成多項式的循環碼.

定理3.2設Cs是由上述序列s∞定義的循環碼，則

(1)Cs的生成多項式為

其中mαj(x)是αj的極小多項式.

(2)Cs是參數為［n，n-3m-1，d］的循環碼，其中

證明(1)由st的定義可知，

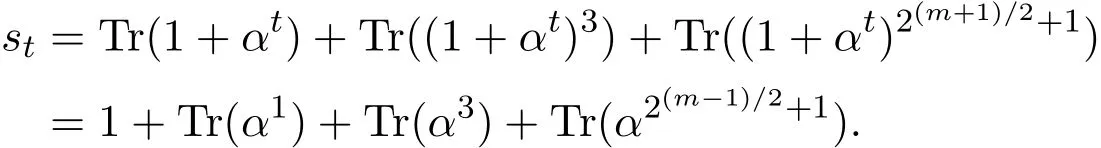
又由引理2.1可知，2-分圓陪集C1，C3，C2(m-1)/2+1所含元素個數均為m個，且它們兩兩不相交.綜合引理2.2的結論以及st的表達式可知，s∞的線性復雜度為3m+1，Cs的極小多項式是

(2)下面只需要證明Cs最小距離d的下界.熟知以Ms(x)為生成多項式生成的循環碼與以Ms(x)的互反多項式為生成多項式生成的循環碼有相同的重量分布.當m=5時，對任意的t，t∈{0，1，2，3，4，5，6}，αt都是Ms(x)的互反多項式的零點，從而由BCH界可知d≥8.當m＞5時，對任意的t，t∈{0，1，2，3，4}，αt都是Ms(x)的互反多項式的零點，由BCH界可知d≥6.定理得證.

例3.3設m=5，α是GF(2m)?的生成元，α5+α2+1=0.則Cs是以

為生成多項式，參數為［31，15，8］的最優二元循環碼.

例3.4設m=7，α是GF(2m)?的生成元，α7+α+1=0.則Cs是以為生成多項式，參數為［127，105，8］的最優二元循環碼.

[1］馮克勤.糾錯碼的代數理論[M］.北京：清華大學出版社，2005.

[2］Lidl L，Niederreiter H.Finite Fields[M］.Cambridge：Cambridge University Press，1997.

[3］Huffman W.C，Pless V.Fundamentals of Error-Correcting Codes[M］.Cambridge：Cambridge University Press，2003.

[4］Ding C.Cyclic codes from the two-prime sequences[J］.IEEE Trans.Inform.Theory，2012，58（6）：3881-3891.

[5］Ding C.Cyclic codes from APN and planar functions[J］.arXiv：1206.4687，2012.

[6］Antweiler M，Bomer L.Complex sequences over GF（pM）with a two-level autocorrelation function and a large linear span[J］.IEEE Trans.Inform.Theory，1992，38：120-130.

[7］Chien R T.Cyclic decoding procedure for the Bose-Chaudhuri-Hocquenghem codes[J］.IEEE Trans.Inform. Theory，1964，10：357-363.

[8］Dobbertin H.Almost perfect nonlinear power functions on GF（2n）：the Welch case[J］.IEEE Trans.Inform. Theory，1999，45：1271-1275.

[9］Forney G D.On decoding BCH codes[J］.IEEE Trans.Inform.Theory，1995，11（4）：549-557.

[10］Van Lint J H，Wilson R M.On the minimum distance of cyclic codes[J］.IEEE Trans.Inform.Theory，1986，32（1）：23-40.

2010 MSC:94B15

Binary cyclic codes from trinomials over GF(2m)

Zhang Aixian1，Feng Keqin2
（1.Department of Mathematics，Xi′an University of Technology，Xi′an710048，China；2.Department of Mathematics，Tsinghua University，Beijing100084，China）

Cyclic codes are a subclass of linear codes and have wide applications in consumer electronics，data storage systems，and communication systems since they have efficient encoding and decoding algorithms.In this paper，some trinomials over finite fields with even characteristic are employed to construct two classws of binary cyclic codes.Lower bounds on the minimum weight of some cyclic codes are developed.The dimensions of the codes obtained in this paper are flexible.

cyclic codes，trinomial，sequences，finite fields

O236.2

A

1008-5513(2016)04-0380-07

10.3969/j.issn.1008-5513.2016.04.006

2016-07-06.

國家自然科學基金(11401468；11471178).

張愛仙(1984-)，博士，講師，研究方向：代數數論及其應用.