L-fuzzy拓?fù)淇臻g中α-開運(yùn)算及α-緊性

李南南 ，王瑞英

（內(nèi)蒙古師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院，內(nèi)蒙古 呼和浩特　010022）

L-fuzzy拓?fù)淇臻g中α-開運(yùn)算及α-緊性

李南南 ，王瑞英

（內(nèi)蒙古師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院，內(nèi)蒙古 呼和浩特010022）

給出了L-fuzzy拓?fù)淇臻g中L-fuzzyα-開運(yùn)算的定義.然后借助L-fuzzy α-開運(yùn)算給出L-fuzzy拓?fù)淇臻g中L-fuzzy α-緊的定義；其次給出L-拓?fù)淇臻g中開覆蓋及fuzzy α-緊的定義；并分別得到了一些相關(guān)性質(zhì)；最后討論了L-fuzzy拓?fù)淇臻g中L-fuzzy α-緊與L-拓?fù)淇臻g中fuzzy α-緊之間的關(guān)系.

L-fuzzy拓?fù)淇臻g；L-fuzzyα-開運(yùn)算；fuzzyα-緊

1　引言

α-開集是一種推廣型開集，文獻(xiàn)［1］中給出它的定義，在文獻(xiàn)［2］中給出了經(jīng)典拓?fù)淇臻g中緊性理論.在文獻(xiàn)［3］中給出了I-拓?fù)渲芯o性理論，在文獻(xiàn)［4］中給出了L-拓?fù)淇臻g中緊性理論，在文獻(xiàn)［5］中給出了L-拓?fù)淇臻g中緊性理論的新形式，那么是否能夠給出L-fuzzy拓?fù)淇臻g中的α-緊性理論呢？在文獻(xiàn)［6］中給出了L-fuzzy拓?fù)淇臻g中開運(yùn)算的定義，在文獻(xiàn)［7］中給出了L-fuzzy拓?fù)淇臻g中半-p-開運(yùn)算和開運(yùn)算及其相關(guān)性質(zhì)，在文獻(xiàn)［8］中給出了L-fuzzy拓?fù)淇臻g中半-p-緊性的概念及其相關(guān)性質(zhì)，在文獻(xiàn)［9］中給出了L-fuzzy拓?fù)淇臻g中半-p-開運(yùn)算定義及半-p-緊性理論.本文在以上理論基礎(chǔ)上，給出了L-fuzzy拓?fù)淇臻g中α-開運(yùn)算的定義及α-緊性理論.

下面給出本文常用的一些概念和結(jié)論.

本文中(L，≤，∨，∧，′)是滿足補(bǔ)余律的F格[10]，X是非空集，L中的最大元和最小元記為?和⊥，LX是X上所有L-集.LX中的最大元和最小元記為?和⊥.L中元素a稱為素元當(dāng)且僅當(dāng)若a≥b∨c有a≥b或a≥c.L中元素a，若a′是素元，則稱a為余素元.L中全體非零余素元記為M(L).

定義L上的一個(gè)二元關(guān)系?：a，b∈L，a?b??對(duì)于任意的非空集D?L，若supD≥b，則存在d∈D使得a≤d.在完全分配格L中，任意b∈L，b=∨{a∈L|a?b}，集合{a∈L|a?b}稱為b的極大極小集[13-14]記為β(a).

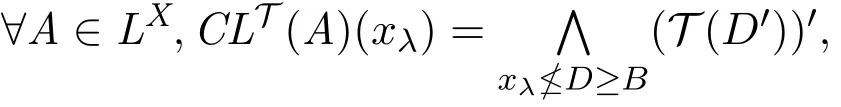
定義 1.2[15-18]若映射T：LX-→L滿足：

(1)T(?)=T(⊥)=?；

(2)?U，V∈LX，T(U∧V)≥T(U)∧T(V)；

則稱T是X上的L-fuzzy拓?fù)洌?X，T)稱作是X上的L-fuzzy拓?fù)淇臻g，稱T(U)是U一個(gè)開集的度.

對(duì)于任意的a∈L和映射T：LX-→L，采用文獻(xiàn)［19］中的記號(hào)

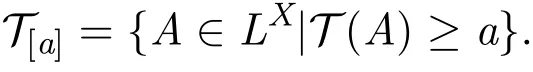
定理 1.1[20]映射T：LX-→L，有以下等價(jià)命題：

(1)T是X上的L-fuzzy拓?fù)?/p>

(2)對(duì)于?a∈M(L)，T[a]是X上的L-拓?fù)?/p>

定理1.2[5]設(shè)(X，τ)是L-拓?fù)淇臻g，A∈LX，若A≤A?-?，則稱A是τ中的α-開集.定義1.3[5]設(shè)(X，τ)是L-拓?fù)淇臻g，G∈LX，如果對(duì)于LX的任意α-開子集U，有

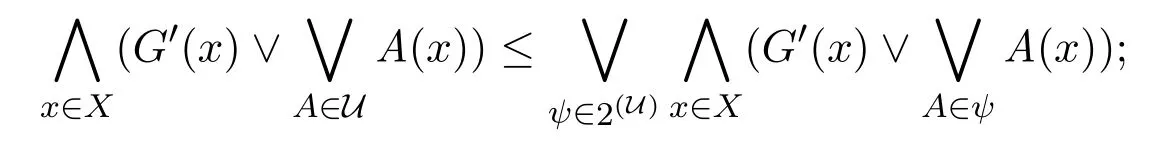
則稱G是fuzzy α-緊.這里2(U)是U的所有有限子集的集合

2　L-fuzzy拓?fù)淇臻g中 α-開運(yùn)算

定義2.1 設(shè)T是X上的L-fuzzy拓?fù)洌x映射Tα：LX-→L如下：

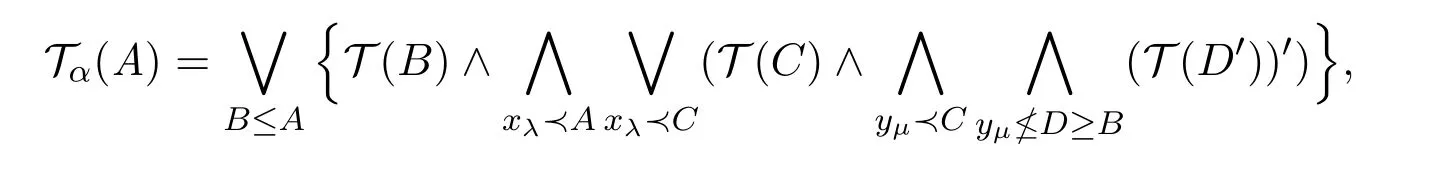
這時(shí)稱Tα是由T誘導(dǎo)的L-fuzzy α-開運(yùn)算，Tα(A)稱A是一個(gè)α-開集的度.

證明若?i∈I，a/≤bi，a≤?=bi∨b′i，

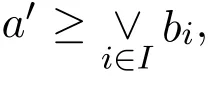
知a≤a′，a∧a≤a′∧a.由a′∧a=⊥得a≤⊥，矛盾！

引理2.2(X，T)是L-fuzzy拓?fù)淇臻g，給定a∈M(L)和T[a]，則

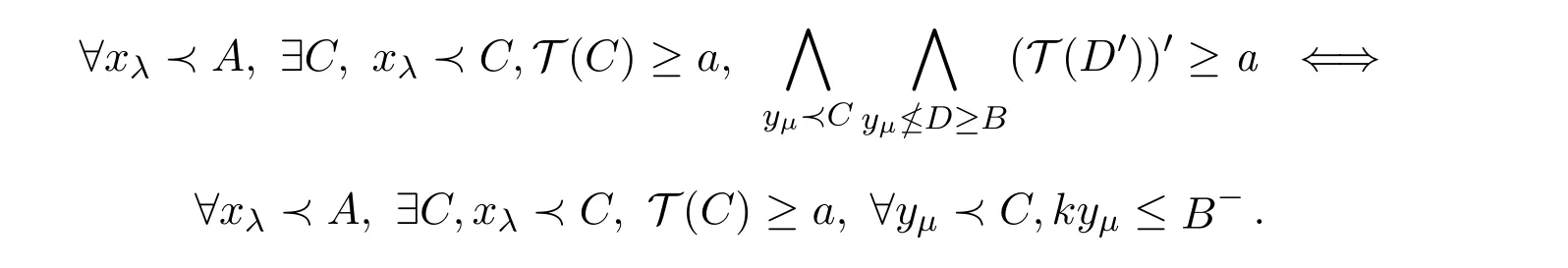
證明(?)只需證?yμ?C，有yμ≤B-，，如若不然?y′μ?C，有y′μ/≤B-，則由B-≥B，得y′μ/≤B-≥B，而B-′∈T[a]，則T(B-′)≥a，(T(B-′)′≤a′，因此

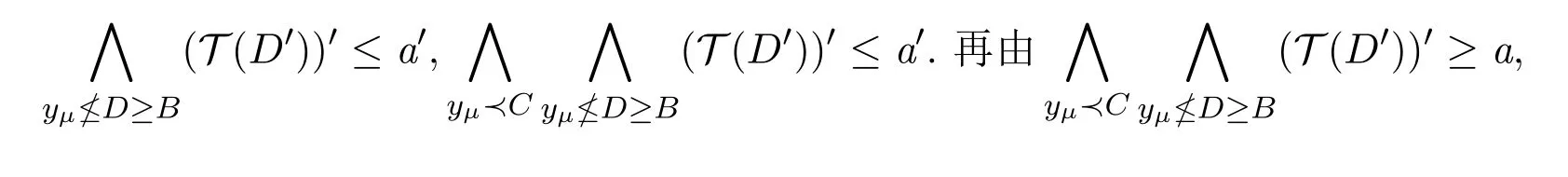
得a≤a′，便有a=a∧a≤a′∧a=⊥，矛盾！(?)只需證

則 ?D?，y′μ/≤D?≥B，(T(D?′))′/≥a，且又有T(D?′)/≥a，若不然T(D?′)≥a，則D?′∈T[a]，即 D?是T[a]中的閉集，由D?≥B得 D?≥B-，又由y′μ≤B-得 y′μ≤D?矛盾！所以T(D?′)/≥a，又因?yàn)閍∈M(L)，則a/≤T(D?′)∨(T(D?′))′=?，矛盾！

定理2.3 設(shè)(X，T)是L-fuzzy拓?fù)淇臻g，A∈LX，a∈M(L)，則A∈(Tα)[a]當(dāng)且僅當(dāng)A 是T[a]中的α-開集，其中(Tα)[a]={A∈LX|Tα(A)≥a}.

證明A∈(Tα)[a]?? Tα(A)≥a

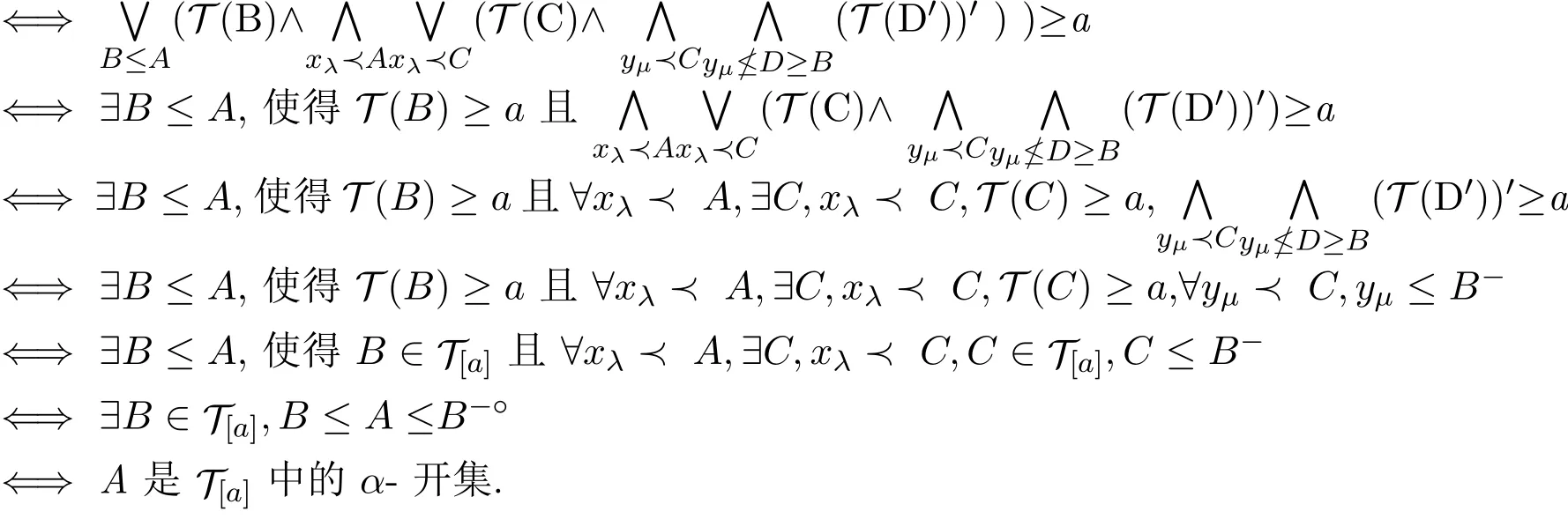
3　L-fuzzy拓?fù)淇臻g中 α-緊性

定義3.1設(shè)(X，T)是L-fuzzy拓?fù)淇臻g，G∈LX，如果對(duì)于LX的任意子集P，有

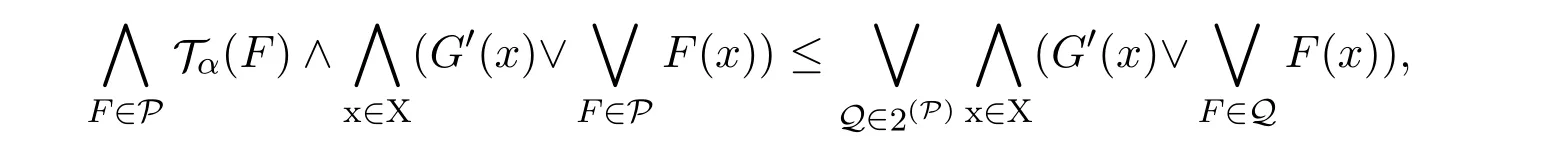
則稱G是L-fuzzy α-緊.這里2(P)是P的所有有限子集的集合

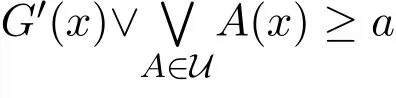
定義3.3 設(shè)(X，τ)是L-拓?fù)淇臻g，a∈M(L)，G∈LX，G稱是a-fuzzy α-緊當(dāng)且僅當(dāng)對(duì)于任意b∈β(a)，G的Qa-α-開覆蓋U，都存在U的有限子集V，V是G的Qb-α-開覆蓋.

定理3.1設(shè)(X，τ)是L-拓?fù)淇臻g，G∈LX，則?a∈M(L)，G是fuzzy α-緊當(dāng)且僅當(dāng)G 是a-fuzzy α-緊.

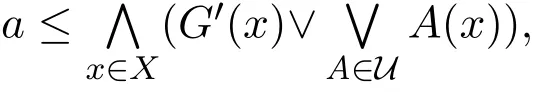
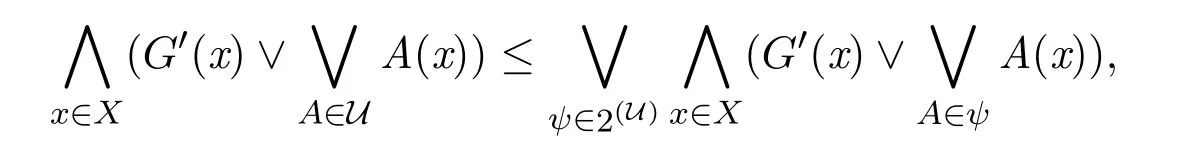
所以

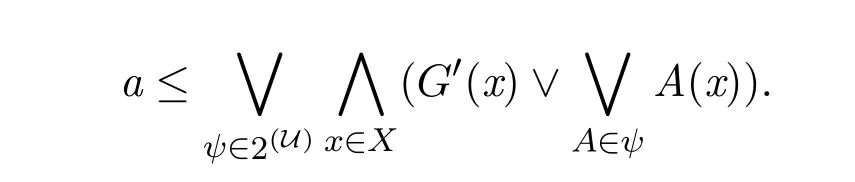
于是

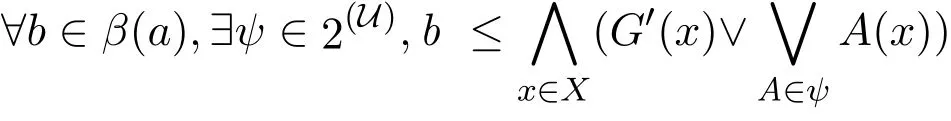
所以G是a-fuzzy α-緊.

(?)對(duì)于LX的任意α-開子集U，

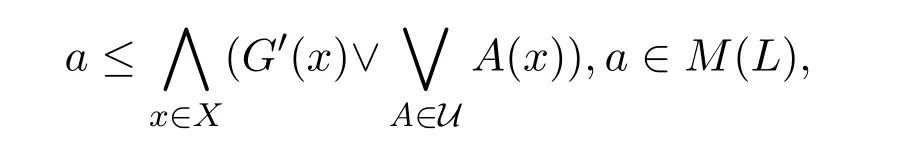
由G是a-fuzzy α-緊，所以?b∈β(a)，?ψb是U的有限子集，ψb是G的Qb-α-開覆蓋，且

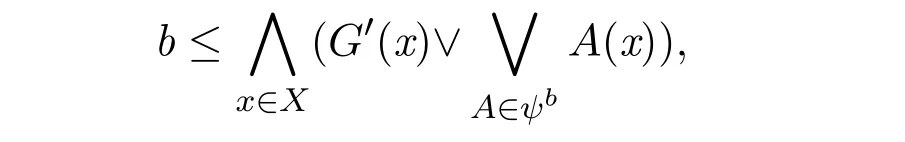
所以

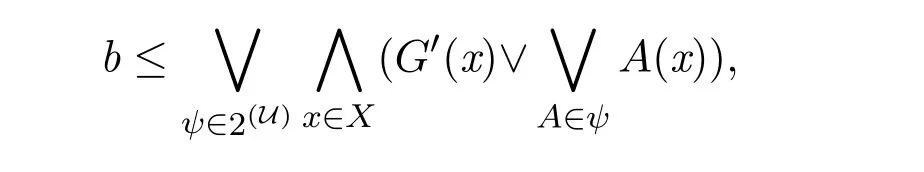
進(jìn)而

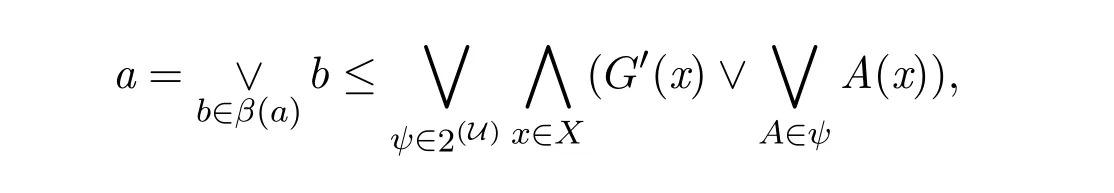
因此

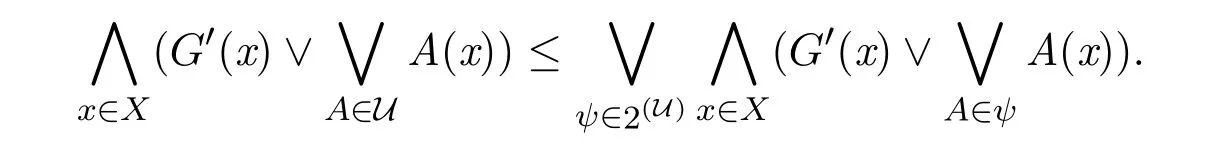
所以G是fuzzy α-緊.

定理 3.2設(shè) (X，T)是 L-fuzzy拓?fù)淇臻g，G∈LX，則 ?a∈M(L)，G在 (X，T)中是L-fuzzy α-緊當(dāng)且僅當(dāng)G在(X，(T)[a])中是a-fuzzy α-緊.

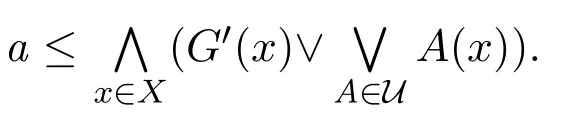
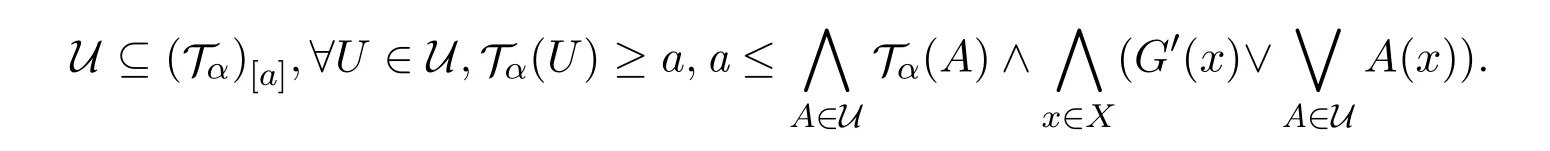
因?yàn)镚在(X，T)中是L-fuzzy α-緊，所以

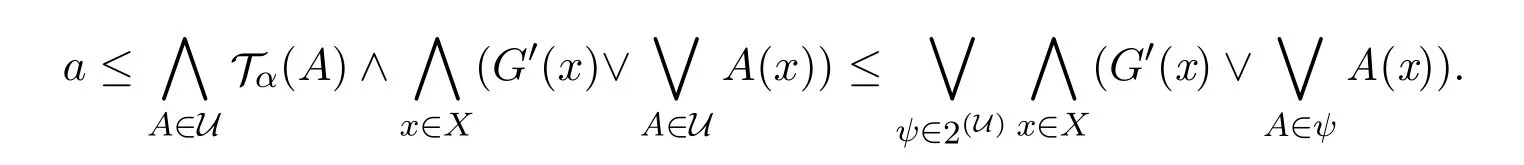
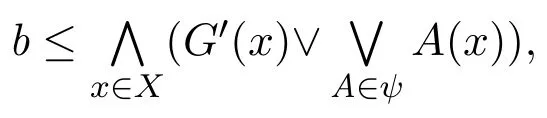
(?)因?yàn)?/p>

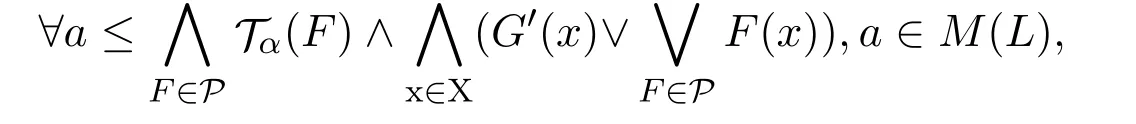
所以

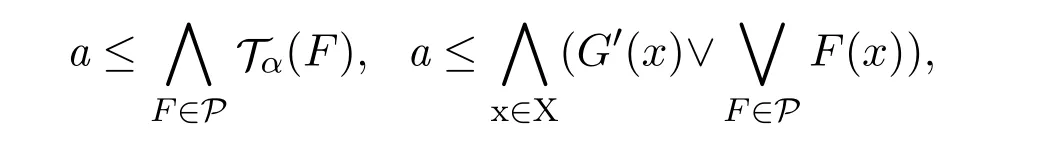
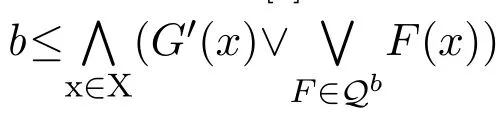
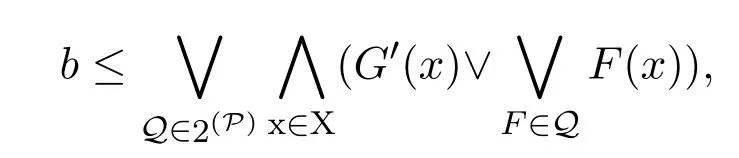
所以所以

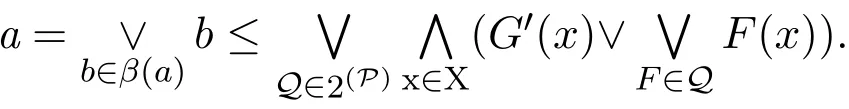
所以G在(X，T)中是L-fuzzy α-緊.

定理3.3 設(shè)(X，τ)是L-拓?fù)淇臻g，a∈M(L)，G、H∈LX若G是a-fuzzy α-緊且H 是α-閉集，則G∧H是a-fuzzy α-緊

證明設(shè)U是G∧H的Qa-α-開覆蓋，?b∈β(a)，?x∈X，有

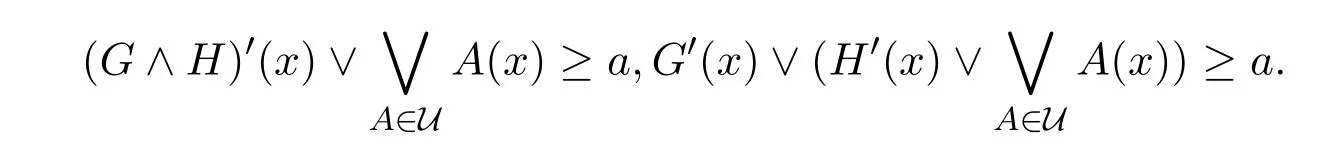
定理 3.4設(shè)(X，τ)是L-拓?fù)淇臻g，a∈M(L)，G，H∈LX若G，H是a-fuzzy α-緊，則G∨H是a-fuzzy α-緊

證明 設(shè)U是G∨H的Qa-α-開覆蓋，?b∈β(a)，則?x∈X，有所以

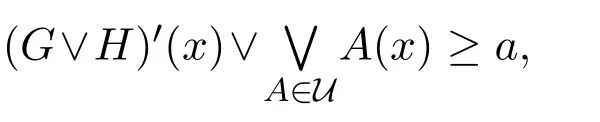
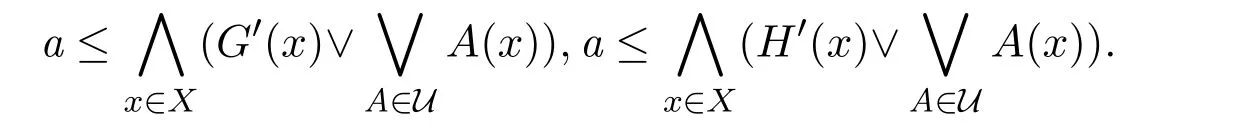
由G，H是a-fuzzy α-緊，則?V1，V2是U的有限子集，V1，V2分別是G和H的Qb-α-開覆蓋，所以

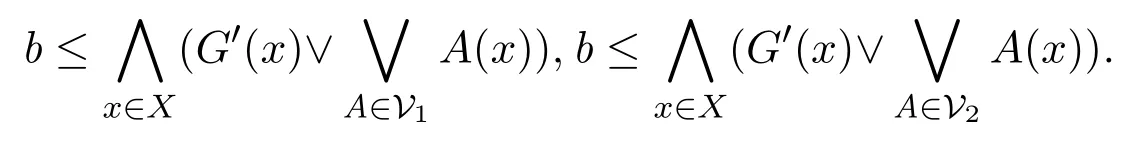
令V=V1∨V2，則V是U的有限子集且

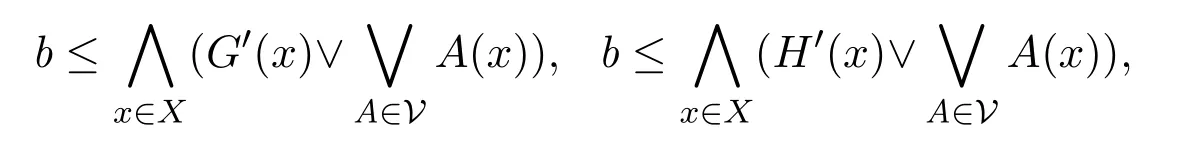
因此

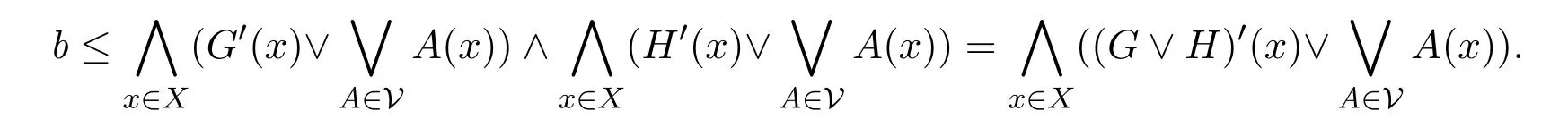
所以V是G∨H的Qb-α-開覆蓋，即得G∨H是a-fuzzy α-緊

定理3.8 設(shè)(X，T)是L-fuzzy拓?fù)淇臻g，G∈LX，若G是L-fuzzy α-緊且Tα(H′)=?，則G∧H是L-fuzzy α-緊

證明由Tα(H′)=?和

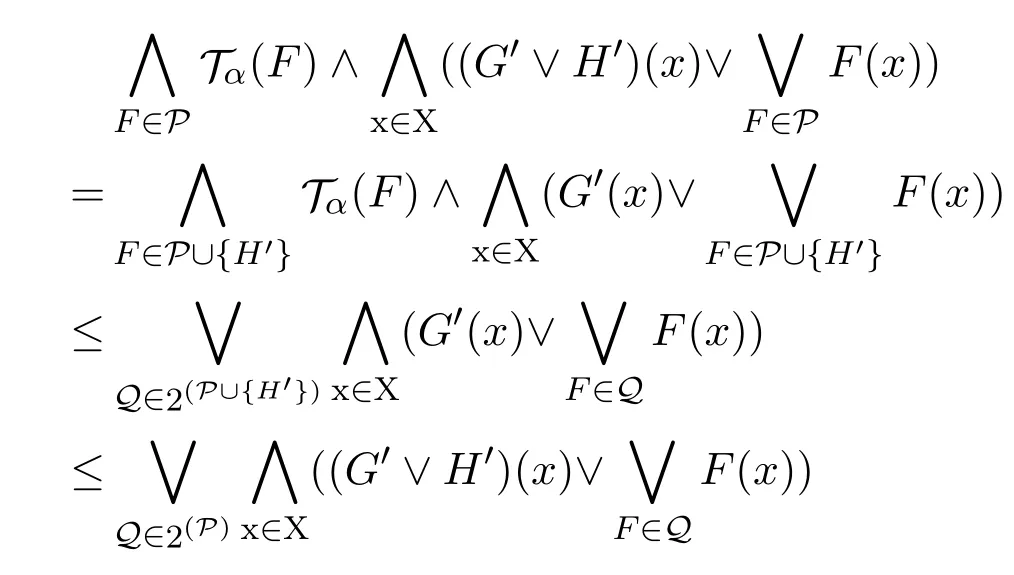
所以G∧H是L-fuzzy α-緊.

4　結(jié)束語(yǔ)

本文給出了L-fuzzy拓?fù)淇臻g中α-開運(yùn)算的定義，在此定義的基礎(chǔ)上研究了L-fuzzy拓?fù)淇臻g中L-fuzzy α-緊，同樣，我們可以在此定義的基礎(chǔ)上，在后面的工作中可以研究L-fuzzy拓?fù)淇臻g中的連通性，分離性等拓?fù)湫再|(zhì)，還可以研究L-fuzzy拓?fù)淇臻g中連通度，緊度等問題。

[1］Njastad O.On some classes of nearly open sets[J］.Pacific J.Math.，1965，5：961-970.

[2］Maheshwari S N，Thakur S S.On α-compact spaces[J］.Bull.Inst.Math.Acad.Sinica，1985，13：341-347.

[3］Thakur S S，Saraf R K.α-compact fuzzy topological spaces[J］.Math.Bohem.，1995，120：299-303.

[4］Ayg¨un H.α-compactness in L-fuzzy topological spaces[J］.Fuzzy Sets Syst.，2000，116：317-324.

[5］Shi Fugui.A new form of fuzzy α-compactness[J］.Mathematic Bohemica，2006，131：15-28.

[6］Shi F G.L-fuzzy interiors and L-fuzzy closures[J］.Fuzzy Sets and Systems，2009，160：1218-1232.

[7］Shi F G.Semicompactness in L-topological spaces[J］.International Journal of Mathematics and Mathematical Sciences，2005，12：225-233.

[8］Shi F G，Li Run xiang.Semicompactness in L-fuzzy topological spaces[J］.Annals of Fuzzy Mathematics and Informatics，2011，1（2）：163-169.

[9］Ghareeb A.L-fuzzy semi-preopen operator in L-fuzzy topological spaces[J］.Neural Comput.Applic.，2012，21（Suppl 1）：87-92.

[10］王國(guó)俊.L-Fuzzy拓?fù)淇臻g[M］，西安：陜西師范大學(xué)出版社，1988.

[11］Gierz G.A Compendium of Continuous Lattices[M］.Berlin：Springer，1980.

[12］Dwinger P.Characterization of the complete homomorphic images of a completely distributive complete lattice[J］.I.Indagationes Mathematicae（Proceedings），1982，85：403-414.

[13］Liu YM，Luo MK.Fuzzy Topology[M］.Singapore：World Scientific，1997.

[14］Wang GJ.Theory of L-fuzzy Topological Spaces[M］.Xian：Shanxi Normal University Press，1988.

[15］Kubiak T.On fuzzy topologies[J］.Ph.D.Thesis，Adam Mickiewicz，Poznan，Poland，1985.

[16］H¨ohle U，Rodabaugh S E.Mathematics of Fuzzy Sets：Logic，Topology，and Measure Theory[M］.The Handbooks of Fuzzy Sets Series，vol 3.London：Kluwer Academic Publishers，1999.

[17］ˇSostak A P.On a fuzzy topological structure，Rendiconti Circolo Matematico Palermo[J］.1985，11（Suppl. Ser.II）：89-103.

[18］Shi F G.Theory of Lβ-nested sets and Lα-nested and their applications[J］.Fuzzy Syst.Math.，1995，4：65-72.

[19］Zhang J，Shi F G，Zheng C Y.On L-fuzzy topological spaces[J］.Fuzzy Sets.Syst.，2005，9：473-484.

2010 MSC:54A40

Regular open set in L-fuzzy Topology

Li Nannan，Wang Ruiying
（College of Mathematical Science，Inner Mongolia Normal University，Huhhot 010022，China）

In this paper，we give the concept of L-fuzzy α-open operator in L-fuzzy topological spaces and use it to obtain L-fuzzy α-compactness in L-fuzzy topological spaces.Moreover we give the concept of open cover and a-fuzzy α-compact in L-topological spaces and its related properties.Finally，We also study the relationship between L-fuzzy α-compactness and fuzzy α-compactness in L-topological spaces.

L-fuzzy topological spaces，L-fuzzy α-open operator，a-fuzzy α-compact

O189

A

1008-5513(2016)04-0499-07

10.3969/j.issn.1008-5513.2016.04.009

2013-07-18.

內(nèi)蒙古師范大學(xué)研究生科研創(chuàng)新基金(CXJJS12030)；內(nèi)蒙古自然科學(xué)基金(2012MS0121，2010MS0118)；內(nèi)蒙古自治區(qū)高等學(xué)校科學(xué)技術(shù)研究項(xiàng)目(NJZY11033).

李南南(1986-)，碩士生，研究方向：模糊拓?fù)?