預設系列問題串，注重關聯式變式
——以“雙一次函數”習題課為例

☉江蘇省蘇州市高新區實驗初級中學練兆明

預設系列問題串，注重關聯式變式
——以“雙一次函數”習題課為例

☉江蘇省蘇州市高新區實驗初級中學練兆明

在一次函數的習題中，常常把兩個一次函數圖像放置在同一平面直角坐標系中，成為“雙直線”圖像問題，根據教學經驗，不少學生對這類問題常常表現出不適應的傾向.而這類問題又非常“復雜”，既有形式復雜但解法簡單的；又有形式簡潔但求解較難的；既有涉及平移、對稱的變換，又有針對一次函數的“斜率”（一次項系數）、常數“轉置”變換的習題等.本文整理近期筆者執教的一節“雙一次函數”習題課教學設計，提供研討.

一、“雙一次函數”習題課教學設計

教學活動一：直線的平移變換

（說明：本課例中圍繞“直線”的系列問題都是在平面直角坐標系xOy中展開探究的，為了節省篇幅，這個條件不再一一描述）

問題1：將直線y＝x向上平移1個單位，所得直線的解析式是______；

問題2：將直線y＝x向下平移2個單位，所得直線的解析式是______；

問題3：將直線y＝-x向右平移1個單位，所得直線的解析式是______；

問題4：將直線y＝-x向左平移2個單位，所得直線的解析式是______.

設計意圖：通4個平移問題引導學生復習直線平移前后的對應關系，即平移方向、單位的關系.特別是后兩種平移（左、右）比前兩種平移（上、下）要復雜，建議學生認真演算，教學時還可跟進舉例，如y＝3x向左（或右）平移2個單位后，所得到的直線解析式是什么？

變式再練1：把直線y＝2x向上平移后得到直線AB，直線AB經過（1，0），求直線AB的解析式.

變式再練2：把直線y＝2x向右平移1個單位后得到直線AB，求直線AB與兩條坐標軸圍成的三角形面積.

教學活動二：直線的翻折變換

問題5：將直線y＝x+1沿x軸翻折后，所得直線的解析式是________；

問題6：將直線y＝x+1沿y軸翻折后，所得直線的解析式是________；

問題7：將直線y＝-2x+b沿x軸翻折后，所得直線的解析式是________；

問題8：將直線y＝kx+b沿y軸翻折后，所得直線的解析式是________.

設計意圖：針對上述4個翻折問題，通過師生對話或追問，可以梳理出直線關于x軸、y軸翻折后對應的直線解析式與原解析式之間的系數變化規律.

變式再練3：將直線y＝-2x+3沿y軸翻折后，所得直線的解析式是________.

變式再練4：若直線y＝2x+2沿x軸翻折后，所得直線與原直線及y軸圍成的面積是多少？

教學活動三：一次函數系數的轉置變換

問題9：若直線y＝2x+n與y軸的正半軸相交，則直線y＝nx+2x經過哪幾個象限？

問題10：兩條直線y＝mx+n與y＝nx+m在同一直角坐標系中的位置可能是圖1中的（）.

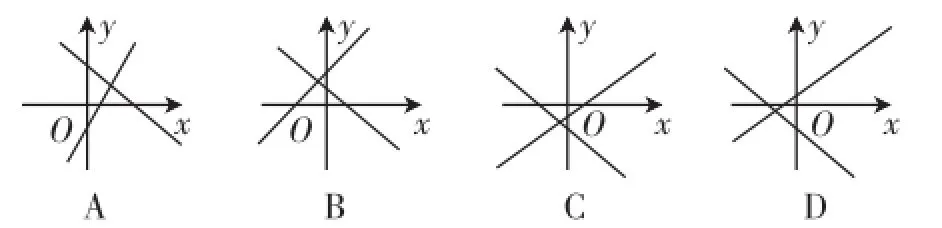
圖1

設計意圖：通過問題9先安排一個系數為常數，再過渡到問題10中兩個參數的轉置思考.

變式再練5：圖2中各函數圖像不可能是一次函數y＝ax-（a-2）圖像的是（）.

圖2

變式再練6：兩條直線y＝ax+b與y＝abx（a，b為常數，且ab≠0）在同一平面直角坐標系中的可能情況是圖3中的（）.

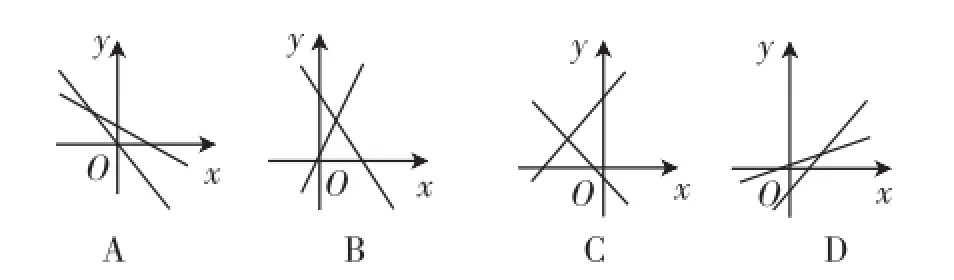
圖3

教學活動四：“雙一次函數”的拓展研究

問題11：已知直線l1：y＝-2x+4與直線l2：y＝0.5x-2.

（1）在同一平面直角坐標系內，畫出這兩條直線；

（2）求這兩條直線的交點坐標；

（3）根據圖像回答，當x在什么范圍內取值時，直線l1在直線l2的上方；

（4）求證：l1⊥l2.

問題12：填表并觀察下列兩個函數的變化情況.

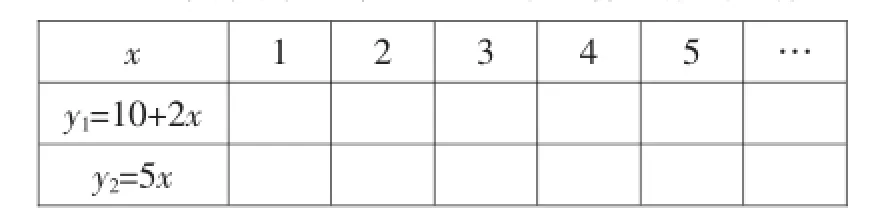
x 1 2 3 4 5…y1＝10+2x y2＝5x

（1）在同一個直角坐標系中畫出這兩個函數的圖像，比較它們有什么不同；

（2）預測哪一個函數值先到2016？

（3）設直線x＝a與（1）中兩個函數的圖像y1＝10+2x、y2＝5x分別交于點M、N.

①當點M在點N上方時，請指出a的取值范圍；

②當MN＝20時，求a的值.

預設講評：第（1）問是開放式問題，通過學生小組內交流后再匯報各自的觀點，并追問有沒有不同的思考，將這個問題的成果擴大.

第（2）問，如圖4，從函數的圖像可知函數y2＝5x的函數值先到2016.這里最好讓學生指出兩條直線的交點，再從交點的意義解讀哪條直線的y值先到2016，更加直觀好懂.

圖4

第（3）問主要是訓練數形結合思想方法在這類雙一次函數問題中的運用.

教學活動五：課堂小結與聽課檢測

聽課檢測題：（5個小題，每小題20分，共100分）

在同一平面直角坐標系中，直線l1： y＝-2x與l2：的圖像如圖5所示.

（1）將直線l1向上平移_____個單位后得到的直線經過點（0，1）；

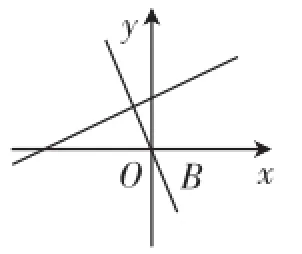
圖5

（2）直接寫出直線l2關于x軸對稱的直線解析式；

（3）當直線l1在直線l2上方時，求出相應的自變量x的取值范圍；

（4）若直線l3：y＝（m-4）x-2與直線l2的交點在第一象限，試分析直線y＝-2x+m-3經過哪幾個象限；

（5）設直線y＝n與l1、l2分別交于點M、N，當MN＝5時，求a的值.

二、教學立意的進一步闡釋

1.預設系列問題串，驅動課堂教學進程

從上面提供的課例來看，我們設計了大量的問題串，意圖通過上述系列問題串驅動課堂教學進程.這些問題串又分成幾個不同的版塊或主題，在每一個主題下的問題串聚焦于一個專題，如教學活動一中我們主要關注的是直線平移的問題，活動二中的4個問題串主要訓練的是直線關于坐標軸翻折的問題.上述兩個活動中系列問題讓學生復習了兩條直線的位置與待定系數之間的關系，也為后續問題的深入研究奠定了基礎.

2.倡導對話與生成，追求開放數學教學

當下倡導的“以學生為主體”、“以學為中心”的課堂教學，根本上說需要教師功在課前、前置思考和精心預設，包括預設追問、點評，在課堂教學時注意通過恰時恰點的問題促進師生、生生之間的對話與精彩生成，這些努力事實上也是追求所謂的“開放的數學教學”（鄭毓信語）.比如，在問題12中，我們設計了“預測哪一個函數值先到2016”就是一個開放式問題，學生的解答和闡釋的方式可能會有很多，判斷的結果并不重要，重在追問學生預測的理由和依據，如果學生的數形結合思想足夠深刻，則可能有非常簡潔有力的解釋.

3.注重關聯式變式，舉一反三式的訓練

據我們的教學觀摩所見，不少同行的習題課往往是選題零亂，缺少主題聚焦.事實上，這也是我們設計上述課例的主要追求，即追求不同問題串之間的關聯式變式，并且及時跟進“變式再練”，通過舉一反三式的訓練幫助學生理解、鞏固方法.一直到課堂檢測環節，仍然是回顧全課所學內容，再次簡單改編數據、字母，以每小題20分的方式反饋聽課效果，從我們的教學經驗來看，這種跟進檢測的教學方式“制造”了必要的緊張氛圍，對于目前大班額（50名學生或以上）教學現狀來看，提高教學效率有著現實意義.

三、結束語

習題教學在目前中學數學課堂教學中占據很大的比重，是不得不面對的一種課型，然而這方面的課型研究（主要是相關的教學設計）還不豐富，也沒有得到應有的重視，我們以一節習題課的設計梳理成文，拋磚引玉，期待批判指正.

1.雍亞波.運算更高效，題型更豐富，思考更深入——以“乘法公式的再認識”習題課教學為例［J］.中學數學（下），2015（11）.

2.劉東升.關聯性：一個值得重視的研究領域［J］.中學數學（下），2013（12）.

3.夏建明.一類值得重視的代數運算應用題［J］.中學數學（下），2015（11）.

4.仇錦華.從數學整體觀看單元教學［J］.中學數學教學參考（中），2015（11）.H