鄭州市的交通擁堵治理及霧霾治理的協調問題
胡康靜 魏子鈺
摘 要:隨著經濟的發展,鄭州的機動車數量與日俱增,導致交通日漸擁堵,與此同時空氣質量指數卻每況愈下,本文是針對鄭州市交通擁堵現狀和霧霾進行分析,從而找到兩者的相關性,最后科學的提出如何有效的治理交通擁堵以及霧霾問題。
關鍵字:灰色模擬系統;相關性 minitab軟件;線性規劃 matlab軟件
1 解決的問題
用數學建模的方法解決交通擁堵以及空氣質量的治理問題并進行以下分析:
(1)在現有不變的模式下,進行對2015-2025年鄭州市交通擁堵和空氣質量的發展趨勢預測。
2 模型的建立及求解
2.1 對問題的分析
在問題(1)中,交通擁堵的狀況用通過平均每新建一公里道路增長車輛數來表示。其次空氣質量變化趨勢則用空氣質量指數(AQI)的變化來表示。
2.2 模型的建立與求解
一、考慮運用灰色系統及相關理論進行對未來天氣狀況的預測建模。
X(n)表示第n個數據
GM(1,1)模型的建立
收集得到數據為2013年全年的空氣質量指數,缺失兩天,共363個數據,將其賦值為X
由積分式dY(t)/dt+b1Y(t)=b2
通過matlab編程運行得到表達式y =940929.0*exp(0.000126848*t) - 940825.0
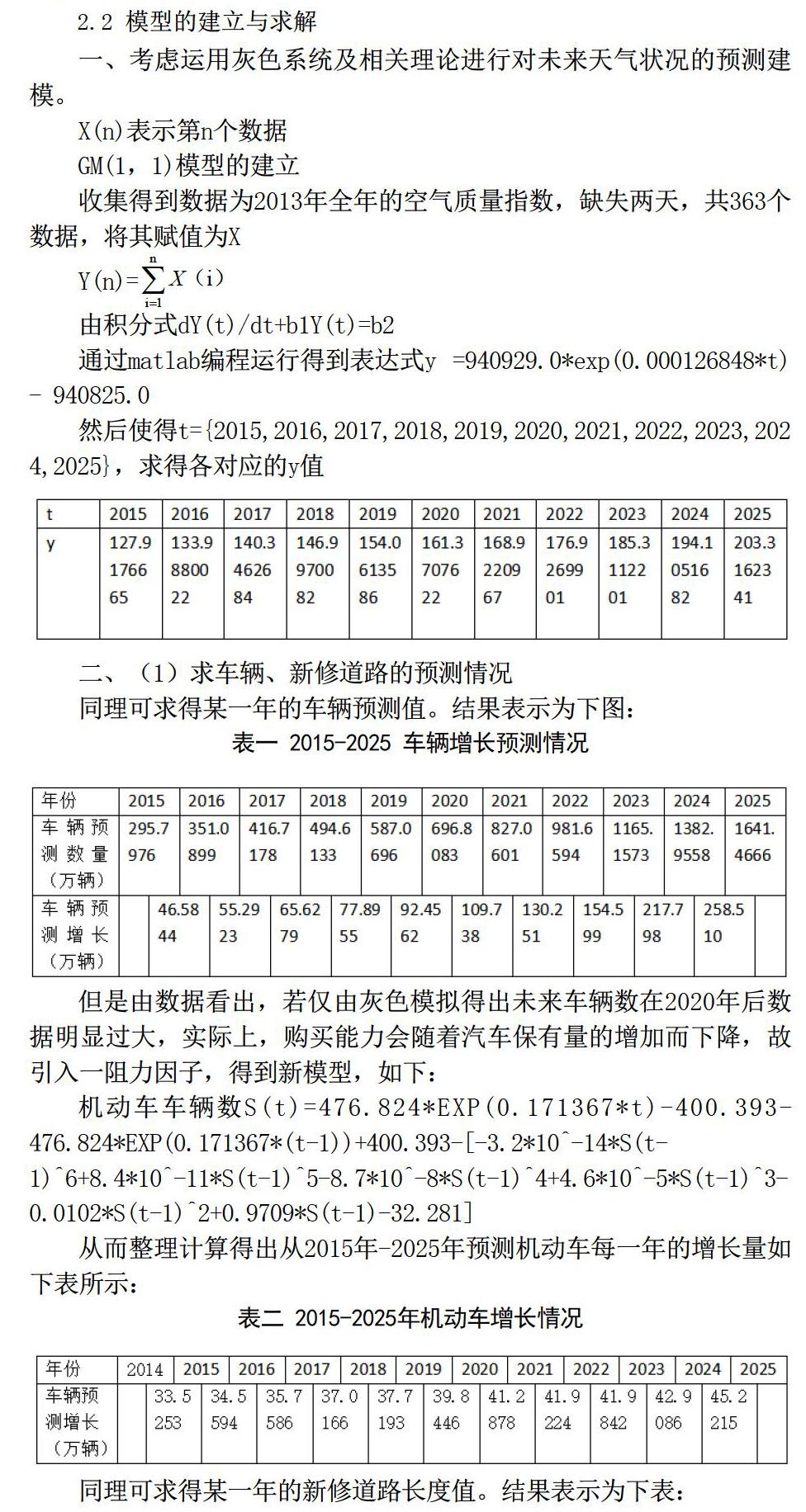
然后使得t={2015,2016,2017,2018,2019,2020,2021,2022,2023,2024,2025},求得各對應的y值
二、(1)求車輛、新修道路的預測情況
同理可求得某一年的車輛預測值。結果表示為下圖:
但是由數據看出,若僅由灰色模擬得出未來車輛數在2020年后數據明顯過大,實際上,購買能力會隨著汽車保有量的增加而下降,故引入一阻力因子,得到新模型,如下:
機動車車輛數S(t)=476.824*EXP(0.171367*t)-400.393-476.824*EXP(0.171367*(t-1))+400.393-[-3.2*10^-14*S(t-1)^6+8.4*10^-11*S(t-1)^5-8.7*10^-8*S(t-1)^4+4.6*10^-5*S(t-1)^3-0.0102*S(t-1)^2+0.9709*S(t-1)-32.281]
從而整理計算得出從2015年-2025年預測機動車每一年的增長量如下表所示:
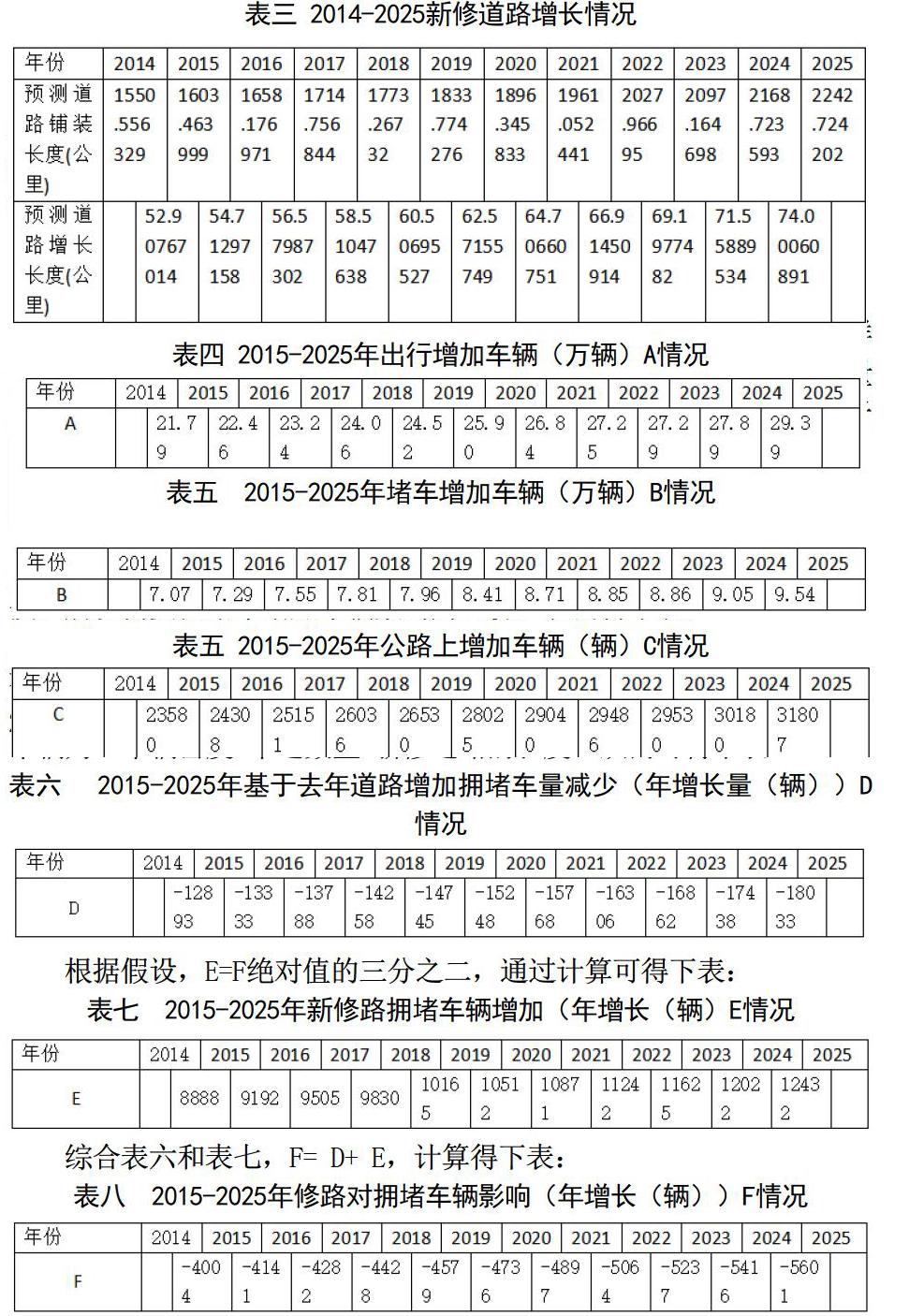
同理可求得某一年的新修道路長度值。結果表示為下表:
(2)增加車輛對交通擁堵的影響
查得鄭州市車輛保有量和上路量之間關系為40~50%,考慮到新車上路機會多,且一車一天可多次出行,以及其他因素的影響等,則最終取得65%的比例關系,得下表:
出行車輛數并不能代表擁堵車輛,因此選取了八個路口作為樣本,某一路口的擁堵車輛數占出行車輛的比例數=(高峰期的車流量數—平峰期的車流量數)/高峰期的車流量數,取平均比例數等于0.324625,用每年出行增加車輛數*0.324625得到下表:
在實際情況中,一天的車輛擁堵高峰期分為早、中、晚三個時間段,所以需要把堵車增加車輛數均為三份,從而得下表:
(3)新修道路對交通擁堵的影響(—:擁堵車量減少,+:擁堵車輛數增加)
理想條件下,由多車道不控制出入一級公路服務水平分級指標,有最大車輛密度(veh/km/ln)<=42,最大服務流率(veh/h/ln)為2000。鄭州的道路車道為六車道。所以基于去年新修道路緩解擁堵的車輛為:車輛密度*車道數量*新修道路的長度。從而可得下表:
根據假設,E=F絕對值的三分之二,通過計算可得下表:
綜合表六和表七,F= D+ E,計算得下表:
(4)修路和公路上增加車輛對擁堵車輛的影響
結合表五和表八,得出修路和公路上增加車輛對擁堵車輛的影響 = 公路上增加車輛+ 修路對擁堵車輛影響,得下表:
3 結果的表示
(1)對于2015-2025年空氣質量的變化趨勢的回答如下:
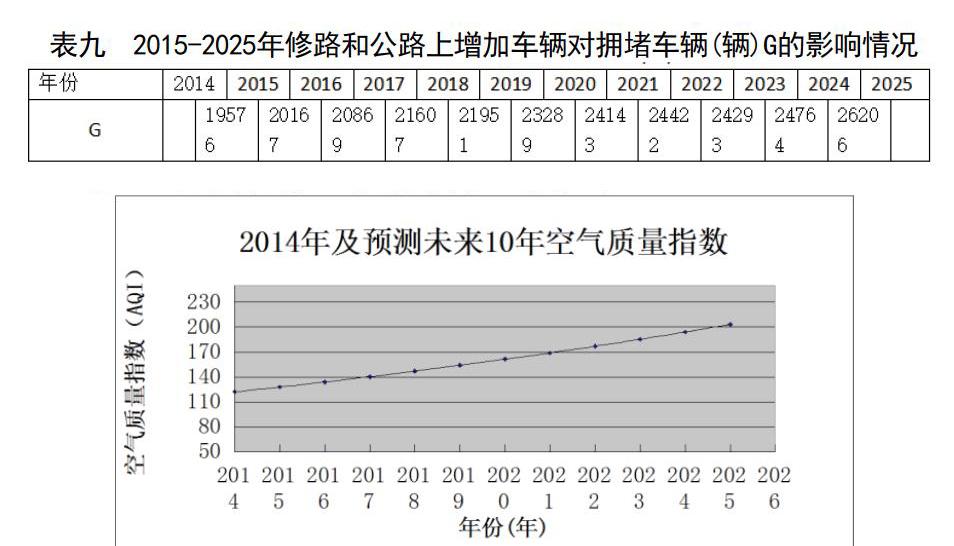
最終整合求得的y、t數據繪制曲線圖如下:
由上圖可得在未來十年里,空氣質量指數逐漸上升,且上升速度有增加的勢頭。
對于2015-2025年交通擁堵的發展狀況的回答如下:
將表九的數據繪制成折線圖如下:
通過上圖可得出結論在未來十年交通的發展狀況將會愈漸擁堵。
參考文獻
[1] 韓中庚,數學建模方法及其應用[M],北京:高等教育出版社,2005
[2] 盛驟,謝式千,概率論與數理統計,北京:高等教育出版社,2003
[3] 費業泰,誤差理論與數據處理(第五版),北京:機械工業出版社,2004.6
[4] 韓中庚,數學建模方法及其應用,北京:高等教育出版社,2005.6

