新課改下的初中數學互動教學實踐研究

胡學年

新課程改革更加重視學生的主體地位，注重發揮學生的主觀能動性，讓學生能夠積極參與課堂互動，激發學習熱情，提高學習效率.課堂教學不是教師一人的表演，而是師生共奏一場優美的交響樂，需要師生互動，教師應更好地了解學生，學生應更好地理解教師.初中數學教學應該重視師生互動，讓學生能夠真正理解數學知識，培養數學思維和方法，促進學生全面發展進步.

一、突出學生的主體地位

初中數學互動教學最為根本的目的是促進學生的學習和發展，互動是一種形式，發展學生綜合能力才是最終的歸屬.新課程背景下，初中數學教學更加重視學生的主體地位，讓學生真正成為學習的主人.教師所有的教學設計、組織和引導都要突出學生的主體地位，讓學生成為臺前最為耀眼的明星，而教師要扮演一個較好的引導者.教師積極與學生合作交流，及時捕捉學生的反應和心理變化，發現他們學習興趣和情緒的變化，調整教學節奏和方法，讓學生與教師始終步調一致，教師和學生同心同德，相互配合，打造優質高效課堂.

我們知道，等腰三角形有下面兩個重要性質：

性質1 等腰三角形的兩個底角相等（簡寫成“等邊對等角”）；

性質2 等腰三角形的頂角平分線、底邊上的中線、底邊上的高相互重合（簡寫成“三線合一”）.

在給學生講解等腰三角形的性質時，如果教師只是通過做頂角的平分線或底邊上的中線把這兩個結論證明出來，會缺少學生的參與，缺少師生的互動，學生只是被動地接受知識，無法突出學生的主體地位.

實際上，可讓學生先動手折出一個等腰三角形，方法如下：

如圖1，把一張長方形的紙按圖中虛線對折，并剪去陰影部分，再把它展開，得到的△ABC就是等腰三角形.

接下來讓學生把剪出的等腰三角形ABC沿折痕對折，找出其中重合的線段和角（可以讓學生合作，如四人為一個學習小組，由組長寫出重合的線段和角），然后根據重合的線段和角得出等腰三角形的性質.

教師通過讓學生動手折疊、觀察圖形，積極參與，主動思考，并進行分組合作，有效地調動了學生探求知識的積極性，真正突出了學生的主體地位.

二、營造積極的互動學習氛圍

學習不僅是一種思維活動，需要智力支持，還需要情感投入.學生喜歡某個老師，或許就會愛上這門學科，就能參與課堂互動，提高學習效率.反之，學生就會厭倦學習，教學效率大打折扣.為此，初中數學教師一定要注重營造良好的課堂環境，鼓勵學生積極參與，讓學生從教師那里得到更多的肯定，從而激發出更多的參與熱情.教師要做學生的良師益友，讓學生能夠感到教師的可親，愿意和教師配合，積極參與互動，勇于表達自己的想法.平等地關愛每一個學生，尤其是學困生，他們更需要教師的愛與幫助.教師營造良好的互動氛圍，充分考慮學困生的基礎和能力，給他們鼓勵，給他們參與互動的機會，幫他們融入課堂，重建自信.

請看下面“全等三角形”復習的一個課例：

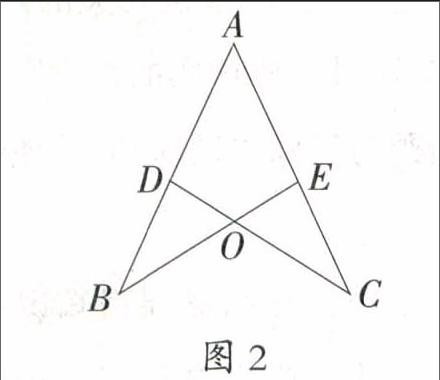
如圖2，點D、E分別在線段AB、AC上，線段BE、CD相交于點O.若AD=AE，要使△ABE≌△ACD，可以添加的一個條件是 .

師：要解決這個問題，我們應該從什么地方入手呢？請大家開動腦筋，認真思考.

生1：先看△ABE和△ACD這兩個三角形有哪些元素對應相等？

師：一般情況下，如果兩個三角形全等，應該有三對元素對應相等，其中至少有一對對應元素是邊.現在添加一個條件，說明已知條件中已有兩對元素對應相等.可是從題目所給的條件來看，我們只能得到AD、AE這一對邊對應相等.還差一對元素對應相等，題目是不是少告訴我們一個條件？

生2：通過觀察圖形發現，∠A是公共角，所以還有一對角對應相等.

師：你觀察得非常細致！題目確實給出兩對元素對應相等.那么應該如何添加全等條件呢？

生3：我認為，在添加全等條件時，既可以從添加邊來思考，也可以從添加角來思考.

師：你考慮問題非常全面，值得大學學習！下面我們先從添加邊來思考.

生4：根據“邊角邊”定理，可以添加“AB=AC”.

師：完全正確！

（從表面上看，若從添加邊思考只能添加“AB=AC”，事實并非如此.教師故弄玄虛，看看學生能不能發現問題.）

師：“接下來我們看看如何添加相等的角.”

生5（非常著急）：老師，還能添加“BD=CE”.

師（故作發愣）：是嗎？這其中有什么道理嗎？

生5：因為AD=AE，如果BD=CE，也可以推出AB=AC.

師：有道理，你確實是個有心人！還能添加哪兩條邊相等嗎？

（看到全班同學無人舉手，教師開始引領學生考慮如何添加相等的角.）

生6：根據“角邊角”定理，可以添加“∠ADC=∠AEB”.

師：very good！

生7：根據“角角邊”定理，可以添加“∠B=∠C”.

師：非常正確.

生8：由“∠ADC=∠AEB”，根據“等角的補角相等”，還可以添加“∠BDO=∠CEO”.

師：聰明.

教師小結：至此，可以添加的全等條件有：“AB=AC”，“BD=CE”，“∠ADC=∠AEB”，“∠B=∠C”，“∠BDO=∠CEO”.

（教師小結完畢，突然有一位學生迫不及待地舉手發言.）

生8：老師，還可以添加“OD=OE”.

師：同學們，生8添加的條件行不行？請大家思考.

（雖然教師知道生8一定有他添加的道理，但并沒有急于讓生8說出添加的理由，而是讓其他學生也思考這個問題.經過思考，陸續有學生舉手.）

生9：添加“OD=OE”可行.因為如果連結AO，根據“邊邊邊”定理，可以證明△AOD≌△AOE，進而可得“∠ADC=∠AEB”.根據“角邊角”定理，知△ABE≌△ACD.

師：看來生8的添法確實有道理.生8和生9都是喜歡動腦、勤于思考的學生.

…………

在這個課例中，教師通過巧妙設計問題，讓優等生、中等生和學困生都能積極參與，都能得到公平對待.教師鼓勵學生積極思考，主動發言，以鼓勵表揚激發他們的參與熱情，課堂氣氛非常活躍，思維得到很好的鍛煉，學習效果明顯，也讓學生養成了較好的學習習慣.