一類帶有治療的乙肝病毒動力學模型的穩定性和Hopf分支

袁曉霞[1]，薛亞奎

?

一類帶有治療的乙肝病毒動力學模型的穩定性和Hopf分支

袁曉霞[1]，薛亞奎

（中北大學 理學院，山西 太原 030051）

建立了一類具有Logistic增長和治療的乙肝病毒動力學模型，分析確定了疾病是否流行的閾值．當時，證明了無病平衡點是全局漸近穩定的，疾病消亡；當時，運用穩定性和分支理論，證明了系統可能出現Hopf分支．數值模擬驗證了理論結果．

乙肝病毒動力學模型；藥物治療；穩定性；Hopf分支

乙肝病毒的動力學研究是針對乙肝病毒的致病機理及流行規律進行理論性分析的一種重要方法．通過建立模型，對疾病的發展和傳播進行預測，為乙肝傳染病的防治提供重要依據．1996年，Nowak等最早提出了乙肝病毒動力學模型[1]．Hews等假設健康肝細胞以Logistic 增長而非常數增長[2]，Min等采用標準發生代替雙線性發生率[3]，這些改進使得模型更接近乙肝疾病的實際傳播，較為合理．近年來，抗病毒治療成為治療乙肝的重要手段，臨床上的抗病毒藥物主要包括干擾素及核苷類藥物２大類，如干擾素和拉米夫定等，他們能有效地抑制乙肝病毒的增殖[4]．本文建立了一類具有Logistic增長和治療的乙肝病毒動力學模型，通過分析確定了疾病是否流行的閾值．

1模型的建立

3系統的Hopf分支

4數值模擬

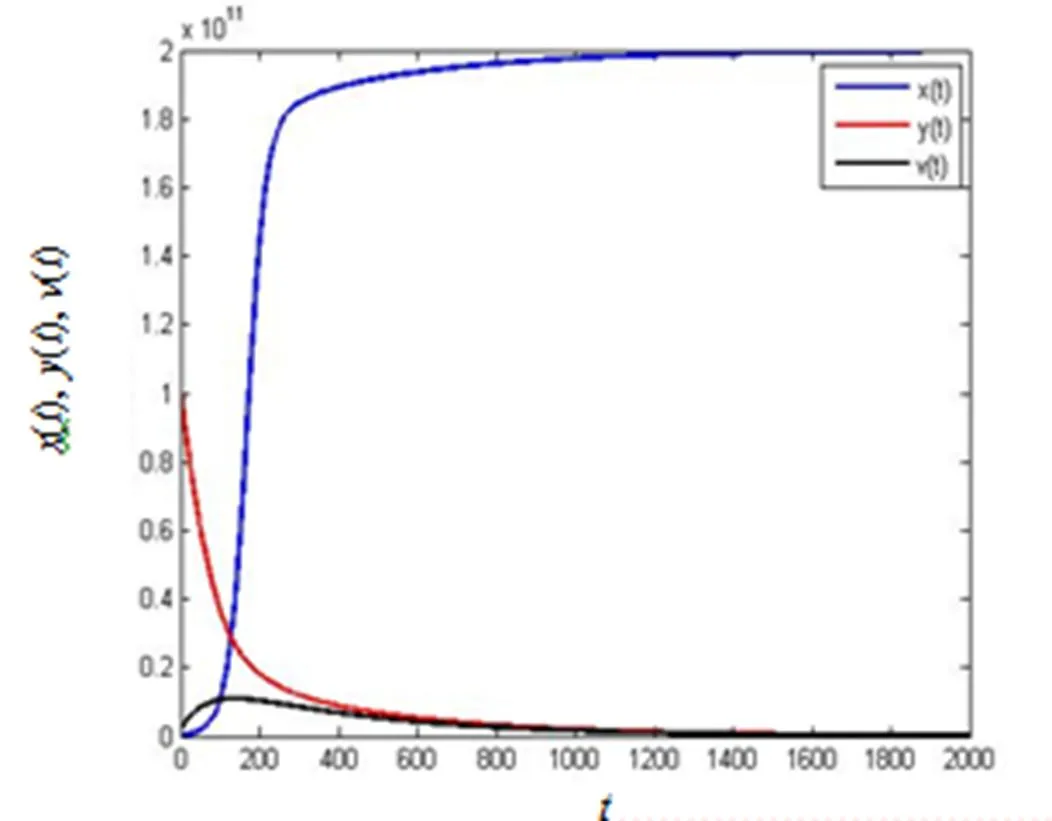
圖1　時，變化曲線

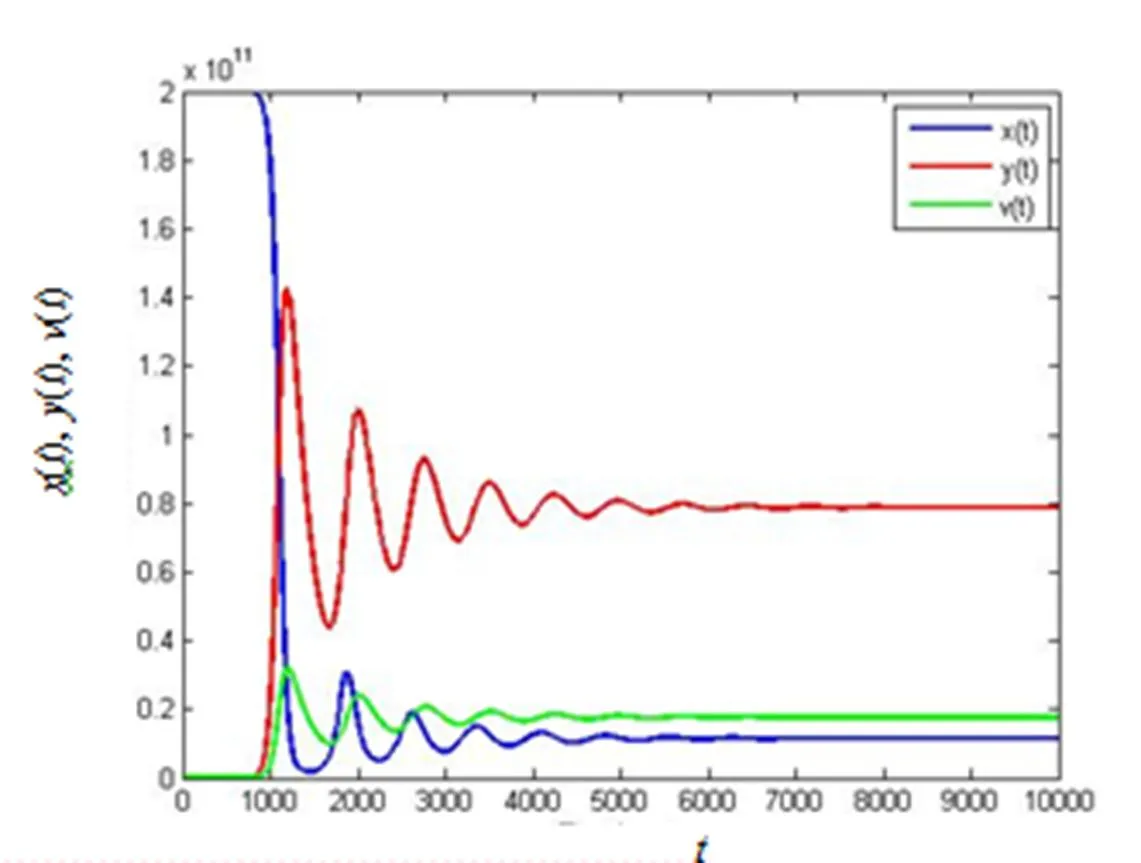
圖2　時，變化曲線

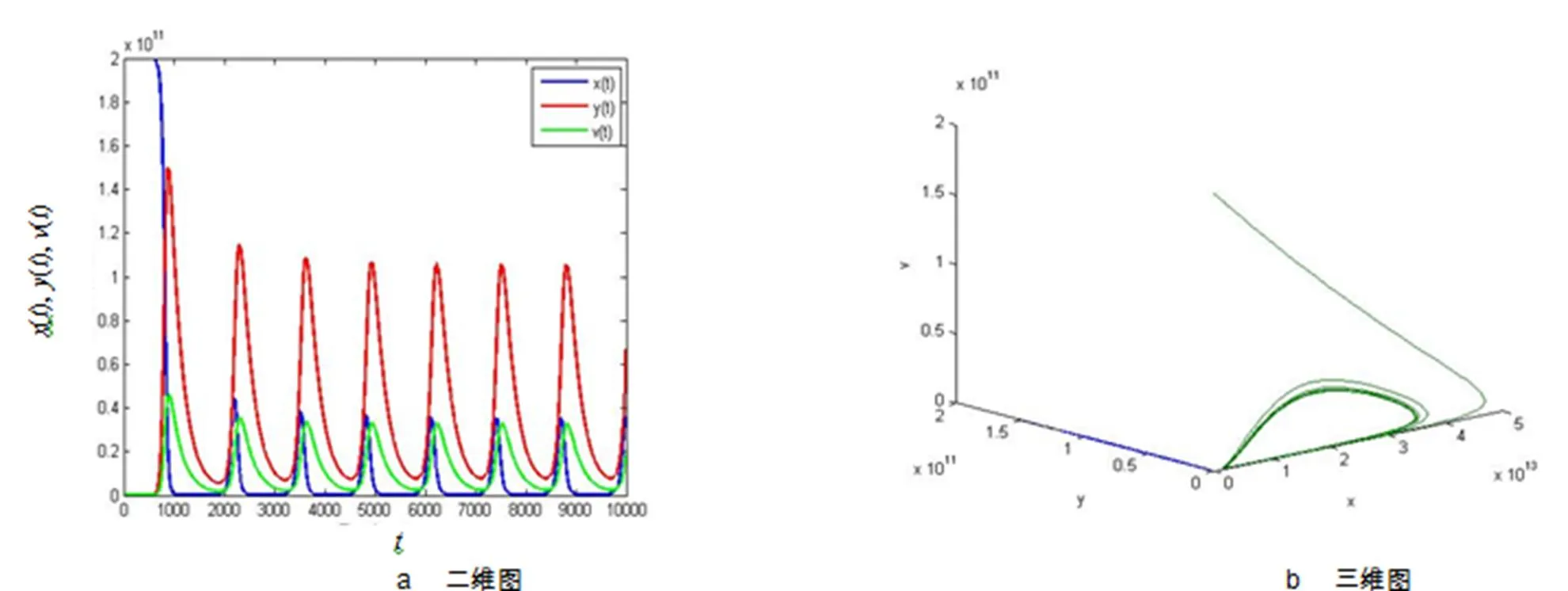
圖3　時，變化曲線

本文研究了一類具有Logistic增長和治療的乙肝病毒動力學模型．分析了平衡點的穩定性，給出了系統發生Hopf分支的臨界條件．通過數值模驗證了理論結果，對預防和控制乙肝傳播具有實際的指導意義．

[1] Nowak M A，Bonhoeffer S，Hill A M，et al．Viral dynamics in hepatitis B virus infection[J]．Proceedings of the National Academy of Sciences，1996，93（9）： 4398-4402

[2] Bonhoeffer S，Coffin J M，Nowak M A．Human immunodeficiency virus drug therapy and virus load[J]．Journal of Virology， 1997，71（4）：3275-3278

[3] Min L，Su Y，Kuang Y．Mathematical analysis of a basic virus infection model with application to HBV infection[J]．Journal of mathematics，2008，38（5）：585-594

[4] Hews S，Eikenberry S，Nagy J D，et al．Rich dynamics of a hepatitis B viral infection model with logistic hepatocyte growth[J]．Journal of mathematical biology，2010，60（4）：573-590

[5] Hattaf K，Yousfi N．Hepatitis B virus infection model with logistic hepatocyte growth and cure rate[J]．Application Mathematical Science，2011，5（47）：2327-2335

[6] Van den Driessche P，Watmough J．Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission[J]．Mathematical biosciences，2002，180（1）：29-48

Stability and Hopf bifurcation for a hepatitis B virusmodel with drug therapy

YUAN Xiao-xia，XUE Ya-kui

（School of Science，North University of China，Taiyuan 030051，China）

Formulated and analyzed a hepatitis B virusdynamics model with Logistic hepatitis growth and drug therapy．Obtained the basic reproduction number，which determines the disease is epidemic or not．Proved that the disease-free equilibrium is globally asymptotically stable and the infection becomes extinct if．When，using theories of stability and bifurcation，it was proved that a Hopf bifurcation may occur．Finally，numerical simulations were presented to verify the theoretical analysis．

hepatitis B virusdynamics model；drug therapy；stability；Hopf bifurcation

1007-9831（2016）02-0001-04

O29∶Q332.4

A

10.3969/j.issn.1007-9831.2016.02.001

2015-12-10

國家自然科學基金資助項目（11301491）

袁曉霞（1990-），女，山西太原人，在讀碩士研究生，從事生物數學研究．E-mail：1244784275@qq.com

薛亞奎（1973-），男，山西太原人，教授，博士，從事生物數學研究． E-mail：xyk5152@163.com