EQUIVALENCE BETWEEN TIME AND NORM OPTIMAL CONTROL PROBLEMS OF THE HEAT EQUATION WITH POINTWISE CONTROL CONSTRAINTS

CHENG Xiao-hong

(School of Mathematics and Statistics，Wuhan University，Wuhan 430072，China）

EQUIVALENCE BETWEEN TIME AND NORM OPTIMAL CONTROL PROBLEMS OF THE HEAT EQUATION WITH POINTWISE CONTROL CONSTRAINTS

CHENG Xiao-hong

(School of Mathematics and Statistics，Wuhan University，Wuhan 430072，China）

In this paper，we study the problem of the equivalence of the heat equation with pointwise control constraints.By making use of the uniqueness of time optimal control，controllability properties and the characterization of norm optimal controls through variational methods，we establish the equivalence between time and norm optimal control problems of the heat equation with pointwise control constraints，and extend the results in the related literature.

bang-bang property；time optimal control；norm optimal control

2010 MR Subject Classification：35K05；49J20；49J30

Document code：AArticle ID：0255-7797（2016）05-0909-11

1 Introduction

There are the following two distinct versions of time optimal control problems［1］：

（i）to reach the target set at a fixed time while delaying initiation of active control as late as possible；

（ii）immediate activation of the control to reach the target set in the shortest time.

In this paper，we shall establish the equivalence between the above two versions of time optimal control problems for an internally controlled heat equation with pointwise control constraints，and their corresponding norm optimal control problems.Let ? be a bounded domain in RN，N≥1，with a sufficiently smooth boundary??.Let ω be an open subset of? and C0（?）=.We formulate time optimal control problems and corresponding norm optimal control problems considered in this paper as follows.

For the first version of time optimal control problems studied in this paper，let T＞0 be fixed.Consider the controlled heat equation

where χ（τ，T）×ωis characteristic function of the set（τ，T）×ω，0≤τ＜T，y1∈C0（?）is a given function，and u（t，x）is a control function taken from the set of functions as follows

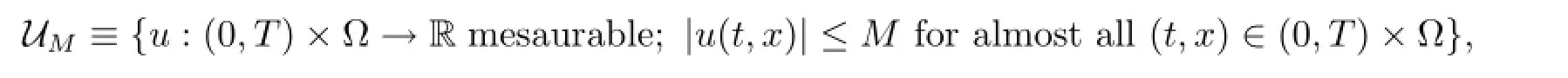
here M is a positive constant.It is well-known that for each u∈L∞（（0，T）×?），equation（1.1）has a unique solution，denoted by y（t，x；y1，χ（τ，T）×ωu）in C（［0，T］；C0（?））.In what follows， we writefor the product sets（0，T）×?，（0，T）×??，（τ，T）×ω and（0，T）×ω，respectively.We shall omit variables t and x for functions of（t，x）and omit the variable x for functions of x，if there is no risk of causing confusion.Now，we are prepared to state the first version of time optimal control problems under consideration

Without loss of generality，we assume that‖y（T，·；y1，0）‖C0（?）＞1.We call

the optimal time for problem（PM）andthe associated time-optimal control（or optimal control for simplicity）with corresponding state，solution of（1.1），satisfying.We call a control u∈UMan admissible control for problem（PM），if there exists some τ∈［0，T）such that‖yu）‖C0（?）≤1.Since the value of the control inhas no effect on the control system（1.1），we consistently assign the control to have the value 0 in

Let τ∈［0，T）be fixed.The norm optimal control problem corresponding to（PM）reads as follows

For the second version of time optimal control problems studied in this paper，we consider the following controlled heat equation

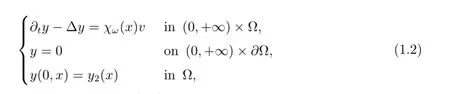
where y2∈C0（?）is a given function，and v（t，x）is a control function taken from the set of functions as follows：

VM≡｛v：（0，+∞）×?→R measurable；|v（t，x）|≤M for almost all（t，x）∈（0，+∞）×?｝，here M is a positive constant.For each v∈L∞（（0，+∞）×?），we denote the unique solution of（1.2）by y（t，x；y2，v）.Now，we state the second version of time optimal control problems under consideration

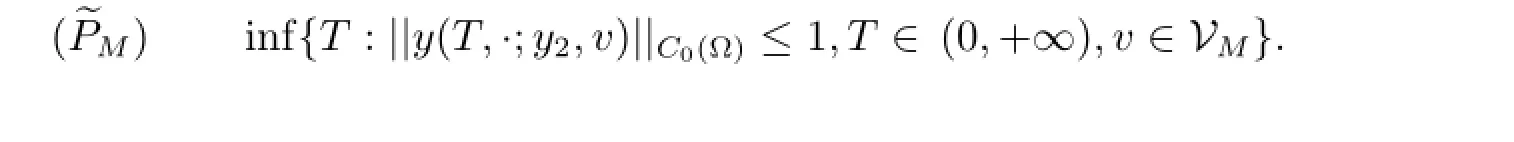
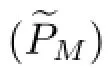
To the beest of our knoewledge，there are few works about equivalence between time and norm optimal control problems for parabolic equations，see［2，3］.In［2］，the equivalence of time optimal control and the norm optimal control was established for abstract equations in Banach spaces.The main differences between［2］and our paper are as follows

（i）The time optimal control problem in［2］is of the second version，while we consider two versions of time optimal control problems.

（ii）The methods for the study of the equivalence between time and norm optimal control problems are different.In［2］，necessary and sufficient conditions for both time and norm optimal controls were obtained，using the argument of separation of target sets from attainable sets.Since those sufficient and necessary conditions have the same form，the equivalence between time and norm optimal controls follows.In our paper，we derive the equivalence directly by making use of the uniqueness of time optimal control，the well known controllability properties and the characterization of norm optimal controls through variational methods as in［4］.

（iii）The paper［2］developed an abstract theory whose applications are limited to the case where the control is distributed in the whole domain which corresponds to the case of ω=? in our study.In our paper，ω is an arbitrarily open subset of ?.The idea of our paper utilizes the approach from［3］.However，there are some main differences between［3］and our paper

（i）The time optimal control problem in［3］was of the second version，while we consider two versions of time optimal control problems.

（ii）The procedure for the study of the equivalence between time and norm optimal control problem is different.We start by researching the optimal norm as a function of time， i.e.，the functionsandWhile in［3］，they began with study of the optimal time as a function of control bounde.

（iii）In our paper，the control constraint is in pointwise form and the target set is a closed ball in C0（?），while in［3］，the control constraint is in integral form and the target setwas a closed ball in L2（?）or 0.Recently，in［5］，the equivalence of optimal target control problems，optimal time control problems and optimal norm control problems were discussed for the heat equation with internal controls.

The main results of this paper are as follows.

Theorem 1.1Let τ∈［0，T）.Then τ=Furthermore，has a unique solution and this solution is also the optimal control to（PN?∞（τ））.Conversely，for eachthe optimal control to（PM）is also the solution toTheorem 1.2 T=T?，?T∈（0，T0］，where T0=inf｛T：‖y（T，·；y2，0）‖C0（?）≤1，T＞0｝.Furthermore，has a unique solution and this solution，when it is exe tended over R+by taking zero value over（T，+∞），is also the optimal control toConversely，for each M∈［0，+∞），the optimal control to，when it is restricted over（0，T?（M）），is also the solution to

It should be pointed out that in［6］，by establishing the connections between（PM） andandas well as strict monotonicity ofandnecessary and suefficient coneditions for optimal time and optimal control of（PM）andewere obtained in［6］.However，the equivalence between time and norm optimal control problems is not proved.

The rest of this paper is organized as follows.In Section 2 and Section 3，we shall give the proofs of Theorem 1.1 and Theorem 1.2，respectively.

2 Equivalence between）PM）and

In this section，we shall prove Theorem 1.1.To this end，we first cite the following lemmas（see［6］）.

Lemma 2.1（i）Assume that τ?（M）is the optimal time for（PM）.Then（PM）has a unique solution，denoted byMoreover=M for almost all（t，x）∈

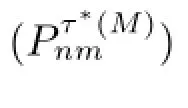
Now，we give some properties about the function τ?（·）.

ProofThe proof is split into five steps.

It suffices to show that if there exists a control u with‖u‖L∞（QT）≤（0）such thatfor a certain τ∈［0，T），then τ=0.By contradiction，τ＞0. Then on one hand，by（ii）in Lemma 2.1，we have that

On the other hand，by the definition ofwe get thatThis together with（2.1）implies thatwhich leads to a contradiction and completes the proof.

Step 2 τ?（·）：→［0，T）is strictly increasing.

Let M1＞M2≥Letbe the optimal control to（PM2）.Then

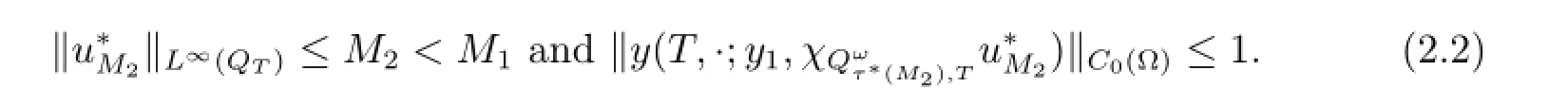
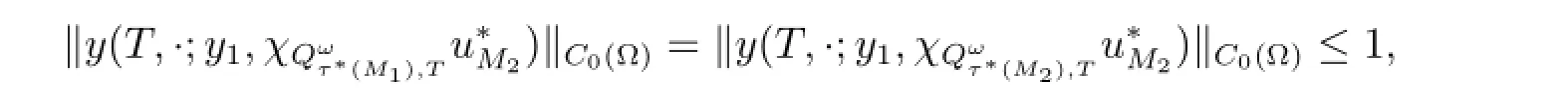
which，combined with the fact that∈UM1，indicates thatis the optimal control to（PM1）.Hence，by（i）in Lemma 2.1，we get that=M1.This contradicts with the first inequality in（2.2）.

Step 3 τ?（·）→［0，T）is right continuous.

Let M?∈be fixed.By Step 2，we infer that τ?（M）exists.We claim that this limit is equal to τ?（M?）.If not，there would exist a sequence Mn↓M?such that

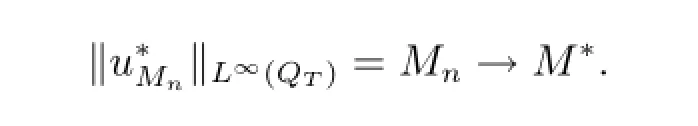
Hence there exist a subsequence ofstill denoted by itself，and∈L∞（QT），such that

and

It follows from（2.3）and（2.4）that

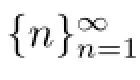
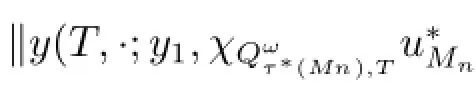
Hence by（2.5）and the above inequality，we get τ?（M?）+δ≤τ?（M?）.This leads to a contradiction.

Let M?∈be fixed and Mn↑M?.It suffices to show that

Consider the following equation

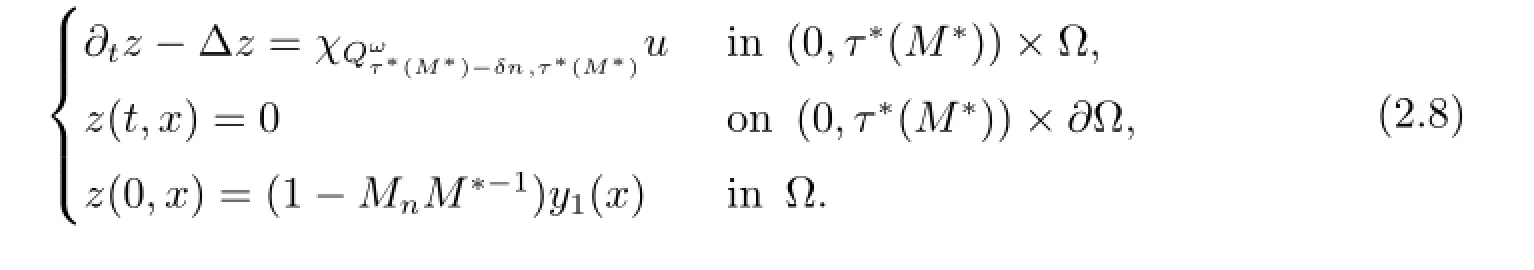
Here δn∈（0，τ?（M?））will be determined later.It is obvious that（2.8）can be rewritten as

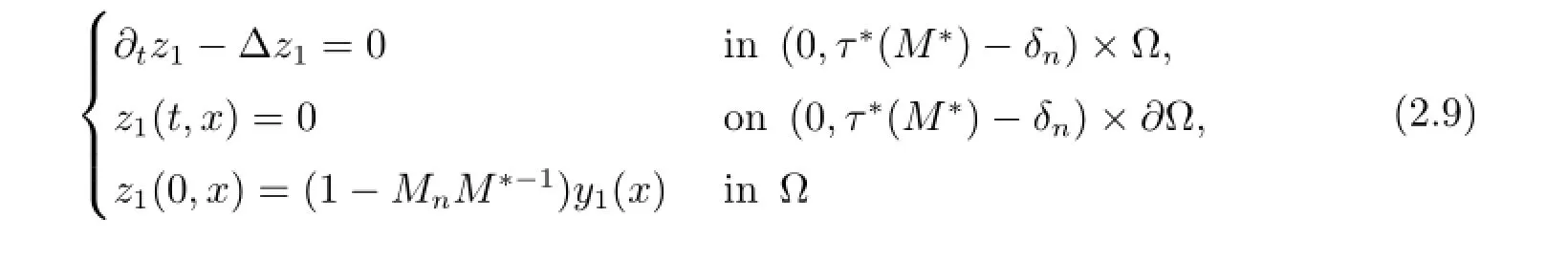
and

where

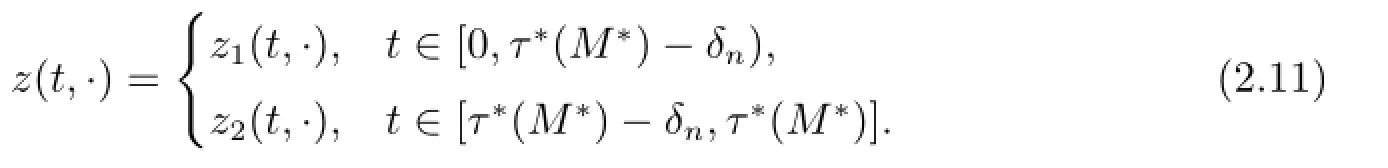
It follows from Theorem 3.1 in［9］and（2.8）-（2.11）that there exists a control，denoted by un，such that the solution of（2.8）corresponding to un，denoted by zn，satisfies

Moreover，

and

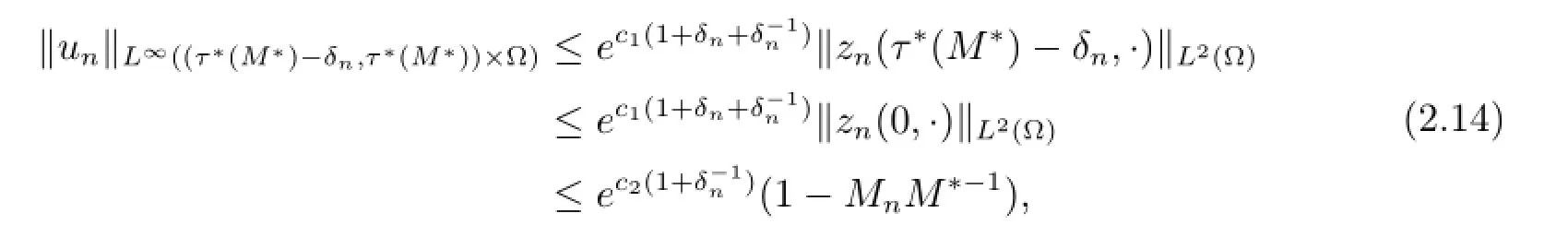
where c1and c2are positive constants independent of n.

and

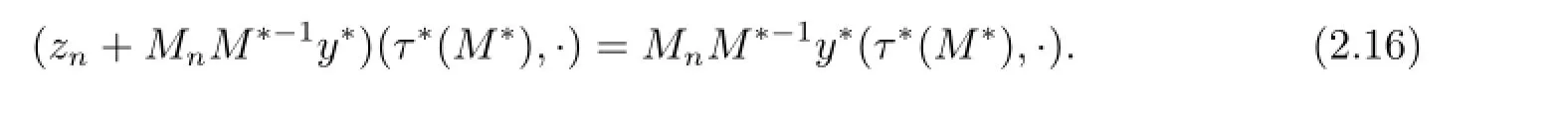
Denote

It follows from（2.15）-（2.17）that

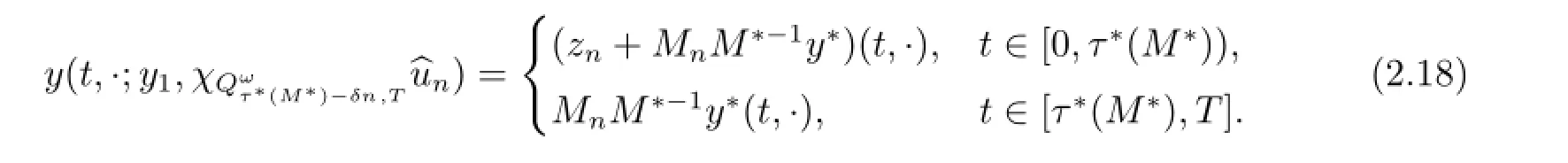
Take

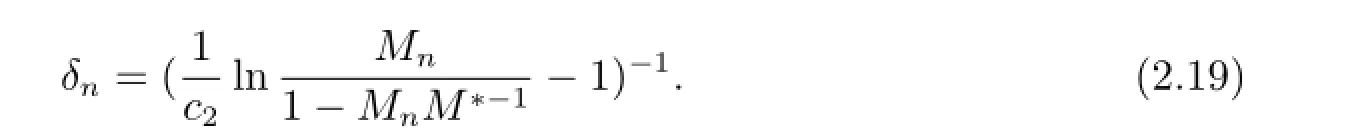
This，together with（2.13），（2.14），（2.17）and（2.18），indicates

and

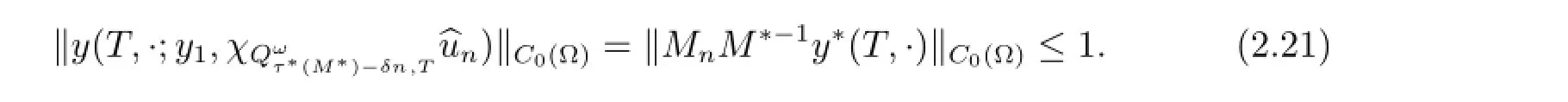
By（2.20）and（2.21），we infer that τ?（M?）-δn≤τ?（Mn），which，combined with the fact that τ?（Mn）≤τ?（M?）and（2.19），implies（2.7）.

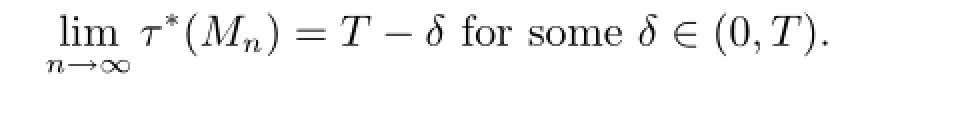
Hence

Consider the following equation：

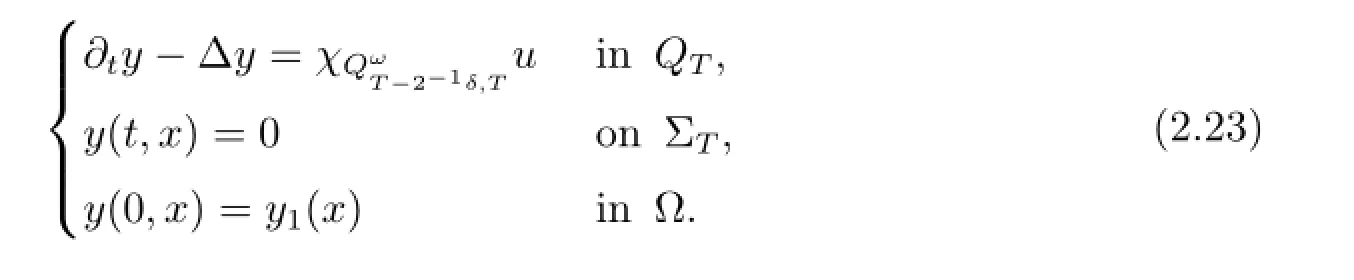
It follows from Theorem 3.1 in［9］and the same arguments to get（2.12）-（2.14）that there exists a control，denoted by uδ，such that the solution of（2.23）corresponding to uδ，denoted by yδ，satisfies

Moreover，

and

here c3is a positive constant.Since Mn↑+∞，by（2.25）and（2.26），we can fix such an n that‖uδ‖L∞（QT）≤Mn.This combined with（2.23）and（2.24）implies τ?（Mn）≥T-2-1δ，which contradicts with（2.22）.

Then we give the proof of Theorem 1.1.

ProofWe first show that

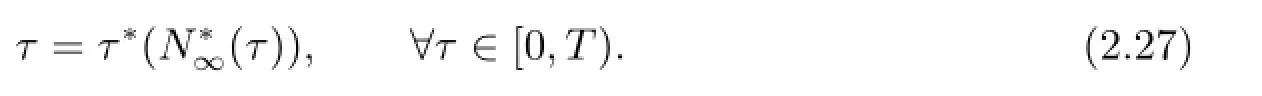
Let τ∈［0，T）and u be a solution to）.Then

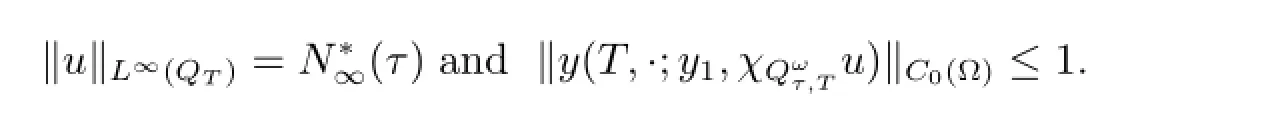
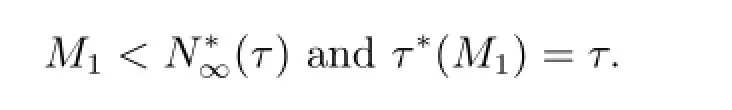
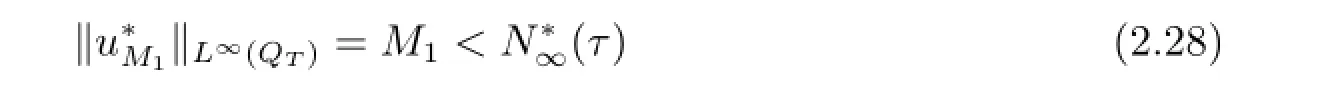
and

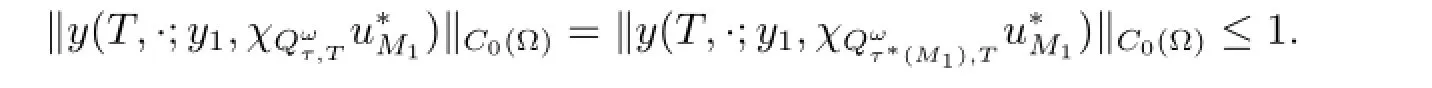
Next，we notice that by（2.27）is the same asThen by（iii）in Lemma 2.1，we deduce that）has a unique solution and this solution is also the optimal control to

3 Equivalence betweenand

In this section，we shall give the proof of Theorem 1.2.For this purpose，we first notice that T0＜+∞（see Lemma 5.6 in［6］）and cite the following lemmas（see［6］）.

Lemma 3.1（i）Let T?（M）be the optimal time for.Thenhas a unique solution，denoted byMoreover=M for almost all（t，x）∈

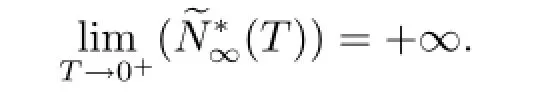
（iii）Let T?（M）be the optimal time forThen problemhas a unique solution.This solution，after being extended to be 0 on［T?（M），+∞）×?，is the optimal control for

Now，we give some properties about the function T?（·）.

Lemma 3.2T?（·）：［0，+∞）→（0，T0］is strictly decreasing，continuous，T?（0）=T0andT?（M）=0.

ProofWe only show that T?（·）：［0，+∞）→（0，T0］is left continuous.Proofs of the remainder are similar as those of［3］or Lemma 2.2.Now，fix M∈（0，+∞）and Mn↑M，we claim that

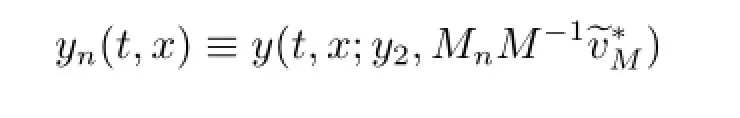
be the solution to the following equation

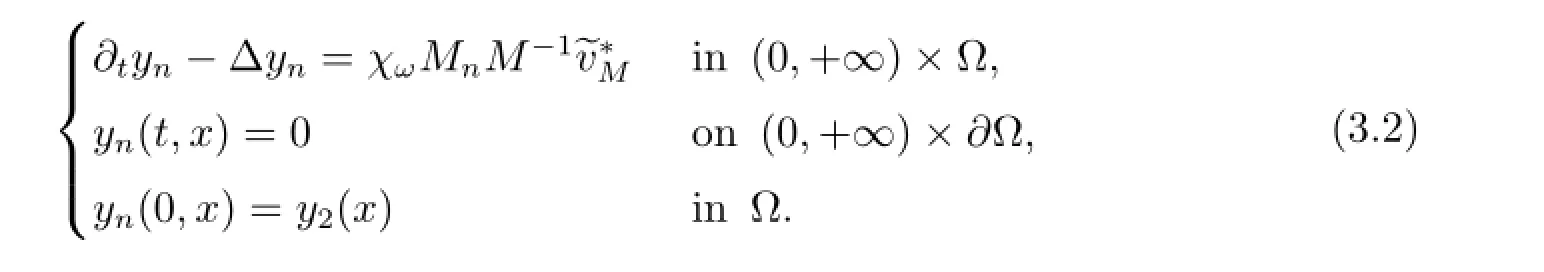
By（1.2），（3.2），Lp-estimate for parabolic equation and embedding theorem（see Theorem 1.14 of Chapter in［7］and Theorem 1.4.1 in［8］），we obtain that

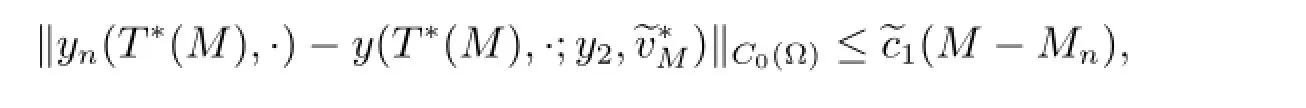
Consider the following equation

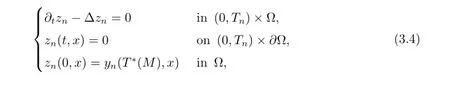
where Tn∈（0，1）will be determined later.Define

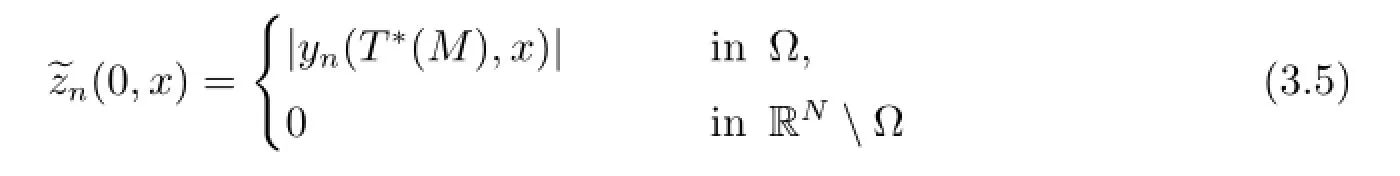
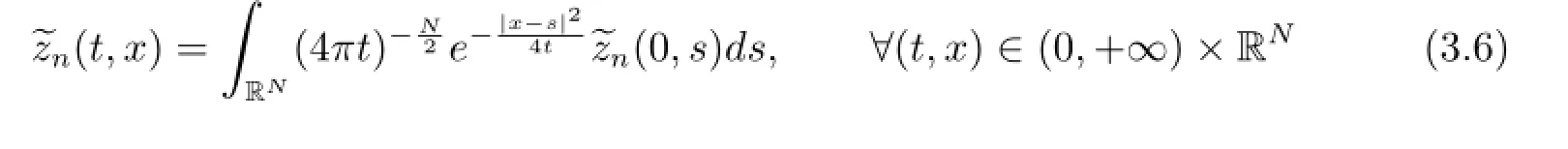
and

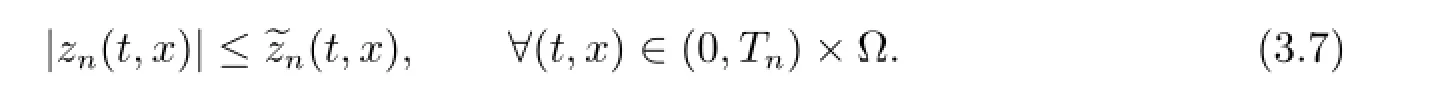
It follows from（3.5），（3.6）and（3.7）that

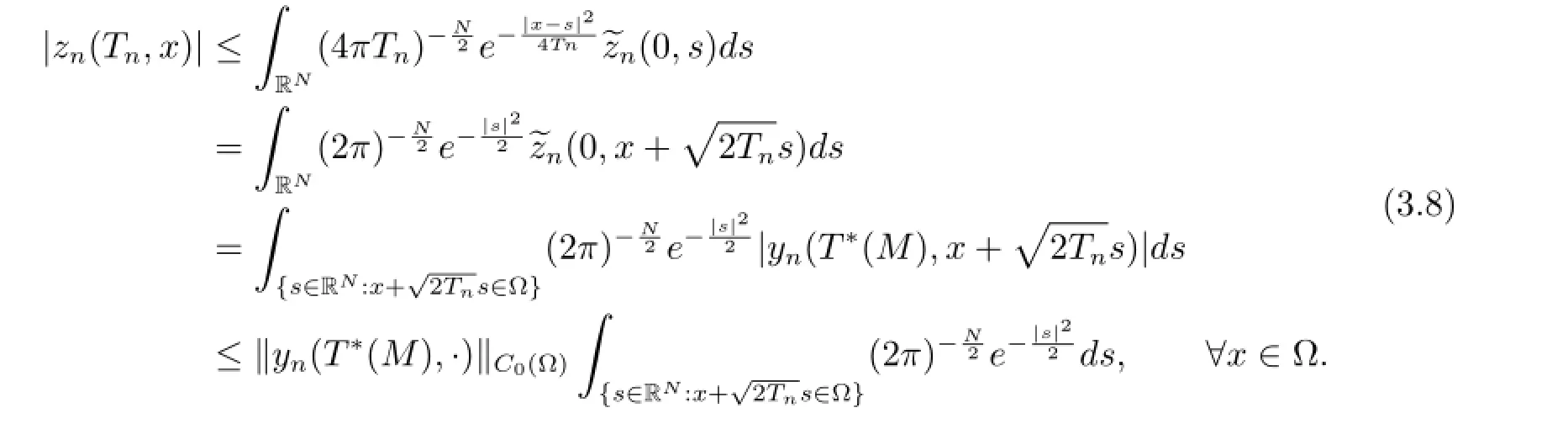
It is easy to check that there exists a positive constantindependent on n such that

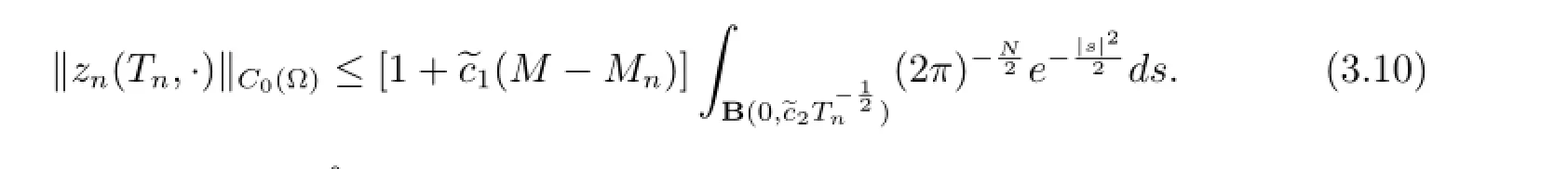
From the latter equality and（3.10），we infer that

Moreover，it follows from（3.2）and（3.4）that

which，together with（3.11），implies

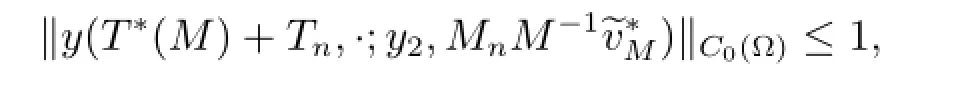
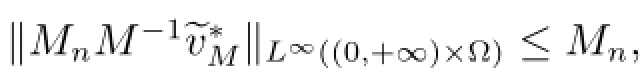
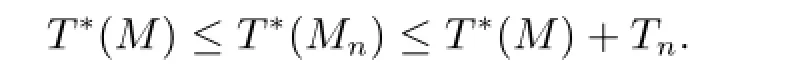
This combined with the limit in（3.11）indicates（3.1）and completes the proof.

Then by the similar arguments as those in［3］（or Theorem 1.1）and Lemma 3.2，we can get Theorem 1.2.

References

［1］Mizel V J，Seidman T I.An abstract bang-bang principle and time-optimal boundary control of the heat equation［J］.SIAM J.Contr.Optim.，1997，35（4）：1204-1216.

［2］Fattorini H O.Infinite dimensional linear control systems：the time optimal and norm optimal problems［M］.North-Holland Math.Study 201，North-Holland：Elsevier，2005.

［3］Wang Gengsheng，Zuazua E.On the equivalence of minimal time and minimal norm controls for internally controlled heat equations［J］.SIAM J.Contr.Optim.，2012，50（5）：2938-2958.

［4］Fabre C，Puel J P，Zuazua E.Approximate controllability of the semilinear heat equation［J］.Proc. Royal Soc.Edinburgh，1995，125 A（1）：31-61.

［5］Wang Gengsheng，Xu Yashan.Equivalence of three different kinds of optimal control problems for heat equations and its applications［J］.SIAM J.Contr.Optim.，2013，51（2）：848-880.

［6］Kunisch K，Wang Lijuan.Time optimal control of the heat equation with pointwise control constraints［J］.ESAIM：Contr.，Optim.Calc.Vari.，2013，19（2）：460-485.

［7］Fursikov A V.Optimal control of distributed：theory and applications［M］.Providence：Amer.Math. Soc.，2000.

［8］Wu Zhuoqun，Yin Jingxue，Wang Chunpeng.Elliptic and parabolic equations［M］.New Jersey：World Sci.Publ.Corp.，2006.

［9］Fern′andez-Cara E，Zuazua E.Null and approximate controllability for weakly blowing up semilinear heat equations［J］.Annales de l'Institut Henri Poincar′e，Analyse Non Lin′eaire，2000，17（5）：583-616.

［10］Wang Xiao，Cui Cheng，Xiao Li，Liu Anping.Existence and uniqueness of solutions for differential equations with time delay and impulsive differential equations with time delay［J］.J.Math.，2013，4：683-688.

具有點態控制約束熱方程的時間與范數最優控制問題的等價性

程曉紅
（武漢大學數學與統計學院，湖北武漢430072）

本文研究了具有點態控制熱方程的等價性問題.利用變分法分析時間最優控制的唯一性，能控性以及范數最優控制的特征，獲得了具有點態控制約束熱方程的時間與范數最優控制問題之間的等價性，推廣了現有文獻的結果.

bang-bang性；時間最優控制；范數最優控制

MR（2010）主題分類號：35K05；49J20；49J30O175.2

date：2015-04-20Accepted date：2015-09-24

Biography：Cheng Xiaohong（1989-），female，born at Hancheng，Shaanxi，master，major in distributed optimal control.