關(guān)于一類廣義Ramanujan-Nagell方程的正整數(shù)解

張正萍，趙開明

（1.重慶科技學(xué)院數(shù)理學(xué)院，重慶401331）

（2.重慶求精中學(xué)，重慶400015）

關(guān)于一類廣義Ramanujan-Nagell方程的正整數(shù)解

張正萍1，趙開明2

（1.重慶科技學(xué)院數(shù)理學(xué)院，重慶401331）

（2.重慶求精中學(xué)，重慶400015）

本文研究了一類廣義Ramanujan-Nagell方程有正整數(shù)解的條件.利用二次域中的重要理論，給出了一個典型的Ramanujan-Nagell方程的所有正整數(shù)解，推廣了文獻［1］和［2］的結(jié)果.

廣義Ramanujan-Nagell方程；正整數(shù)解；二次域

1　引言

設(shè)Z和N分別表示全體整數(shù)和正整數(shù)組成的集合，p是奇素數(shù)，D是適合p/|D的正整數(shù).此時，方程

是一類基本而重要的廣義Ramanujan-Nagell方程.多年來，關(guān)于該類方程的整數(shù)解一直是指數(shù)Diophantus方程的一個引人關(guān)注的問題，但主要是其解數(shù)N（D，p）的上界估計，樂茂華［1］證明了當(dāng)（D，p）=（2，3）或（3s2+1，4s2+1），其中s是正整數(shù)時方程（1.1）恰有2組正整數(shù)解，否則，該方程至多有1組正整數(shù)解；曹珍富［2］僅給出了方程x2+2=3n僅有（1，1）、（5，3）兩組正整數(shù)解.

作為代數(shù)數(shù)論中的重要組成部分，二次域的有關(guān)類數(shù)、理想等相關(guān)性質(zhì)和理想數(shù)唯一分解定理對研究該類方程的整數(shù)解有著重要作用.對某些D＞0，不是Euclid域，若其類數(shù)=1，可以利用代數(shù)整數(shù)環(huán)中唯一分解定理的相關(guān)知識去研究方程的整數(shù)解問題；若其類數(shù)/=1，可以利用二次域中整數(shù)環(huán)上的理想唯一分解定理去研究方程的整數(shù)解問題.為此，先引入同余式、二次域的有關(guān)類數(shù)、理想及其相關(guān)性質(zhì)和理想唯一分解定理.

定義1.1［3］若ε和ε-1都是代數(shù)整數(shù)，則ε稱為單位數(shù).

定義1.2［4］環(huán)R的非空子集S叫做R的理想，是指滿足下面條件：（1）如果a，b∈S，則a±b∈S；（2）如果r∈R，a∈S，則ar，ra∈S.

定義1.3［4］由一個元素x∈R生成的理想（x）叫做環(huán)R的主理想，如果R是整環(huán)，并且R中每個理想都是主理想（x）=xR，則R叫做主理想整環(huán).

定義1.4［5］數(shù)域K的子集I叫做K的分式理想，是指存在0/=μ∈Ok（數(shù)域K的整數(shù)環(huán)），使得μI為Ok的非零理想，用I（K）表示K的全體分式理想組成的集合，且I（K）構(gòu)成群，叫做數(shù)域K的分式理想群；對于α∈K，稱αOk（0/=α∈Ok）為主分式理想，而I（K）中主分式理想的全體構(gòu)成一個群，叫做K的主分式理想群，記作P（K）；商群C（K）=I（K）/P（K），叫做K的（分式）理想類群，C（K）中的每一個元素叫做K的（分式）理想類.

定義1.5［5］理想類群的階h（K）=|C（K）|叫做數(shù)域K的類數(shù).

定義1.6［6］設(shè)是一個代數(shù)整數(shù)環(huán)，α1，α2，···，αs∈，把集合

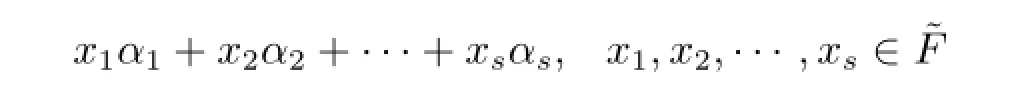
稱為是由α1，α2，···，αs生成的?F中的理想數(shù).

定義1.7［6］設(shè)α，β∈M，若存在ε使β=ε⊙α，則稱β是α的相伴數(shù)，記作β～α.

定理1.1［7］若a≡b（modmi），其中i=1，2，···，n，則a≡b（mod［m1，m2，···，mn］）.

引理1.1［6］α∈A2（全體Q上的2次代數(shù)數(shù)組成的集合）的充要條件是α=r+其中r，s∈Q，s/=0以及D/=0是無平方因子的有理整數(shù)全體Q上的2次代數(shù)整數(shù)組成的集合）的充要條件是除以上所說的外還要滿足2r∈Z，～r2-Ds2∈Z.

引理1.2［6］設(shè)D滿足引理1.1的條件，及

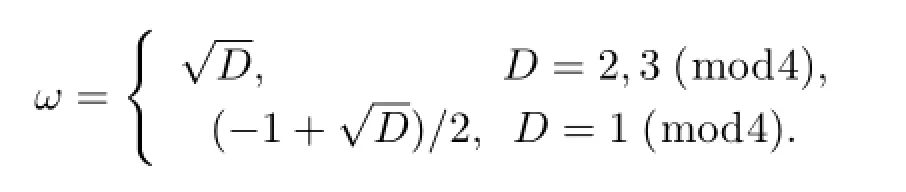
那么α是二次代數(shù)整數(shù)的充要條件是它可以表為

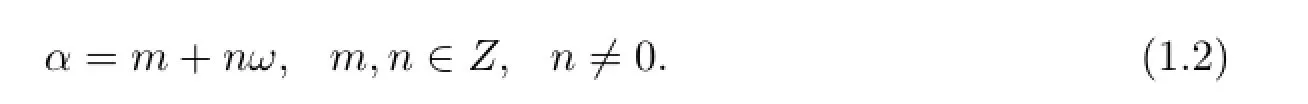
定理1.2［6］當(dāng)D≤-1時，僅當(dāng)D=-1，-3時才有形如（1.2）的單位數(shù).僅當(dāng)D=-1時，這種單位數(shù)是±i，當(dāng)D=-3時，這種單位數(shù)是

定理1.3［6］主理想整環(huán)是唯一分解整環(huán).

定理1.4［6］設(shè)M是唯一分解環(huán)，正整數(shù)k≥2，以及α，β∈M，（α，β）=，那么若αβ=γk，γ∈M，則有α=ε1μk，β=ε2νk，μ，ν∈M，其中ε1，ε2是M中的單位，且ε1ε2=εk，ε為單位.

2　x2+5=pn（n∈N）有正整數(shù)解的必要條件

利用二次域中整數(shù)環(huán)上的理想唯一分解定理，以下證明廣義Ramanujan-Nagell方程

有正整數(shù)解的必要條件.

證情形（1）若n是偶數(shù)，則由（2.1）式可得

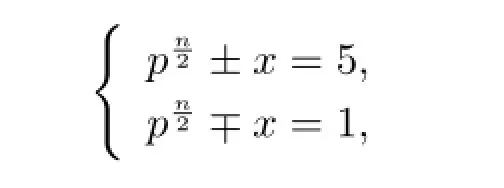
情形（2）若n是奇數(shù)，在虛二次域中，由定義1.4和定義1.5可得的類數(shù)=2，且有單位數(shù)±1，其中1和是一組整基［6］，從而整環(huán)的整數(shù)形如的形式，其中a，b∈Z.由此可得方程（2.1）的理想分解為

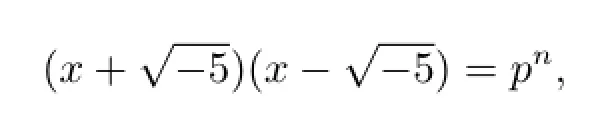
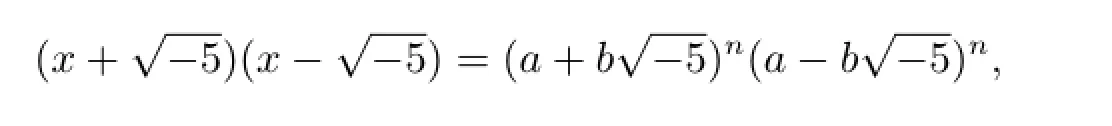
其中a2+5b2=p.從而由定理1.4得

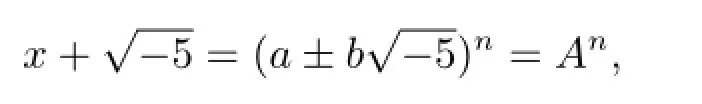
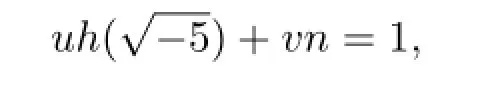
于是有

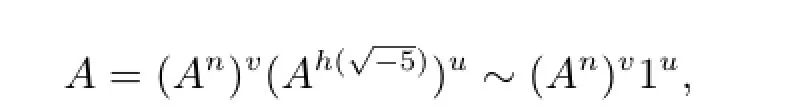
由An～1得A～1v，1u～1，即A是中的主理想.又由中的單位數(shù)是±1，則有

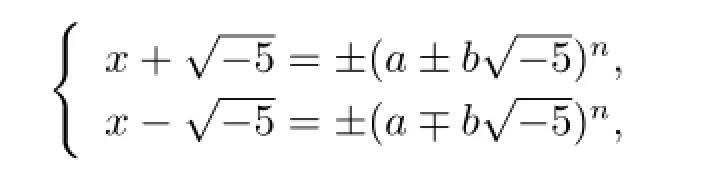
進而有

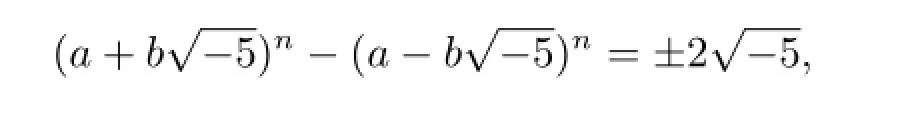
則

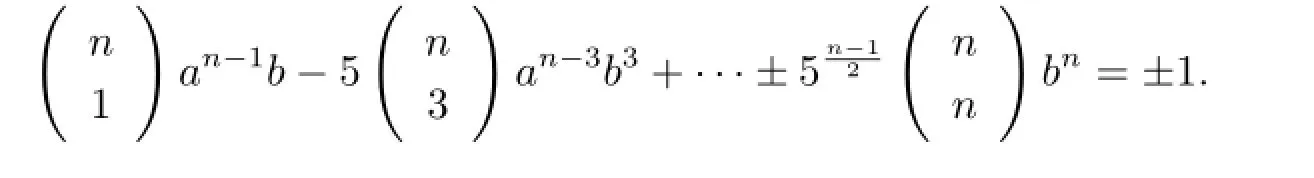
即

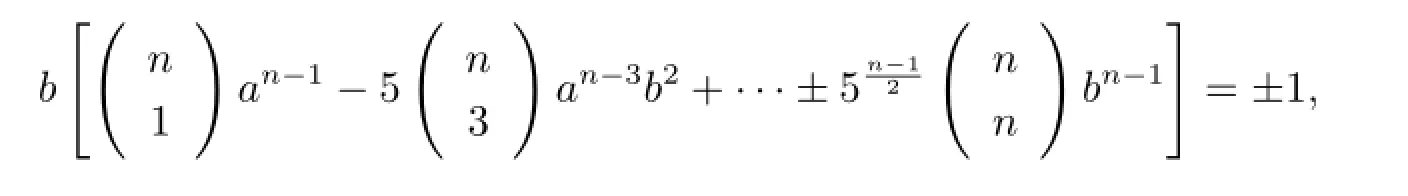
從而b=±1，得證.

3　x2+5=pn（n∈N）正整數(shù)解的證明

以下證明廣義Ramanujan-Nagell方程

僅有正整數(shù)解（4，1）.

證情形（1）若n是偶數(shù)，則由（3.1）式可得

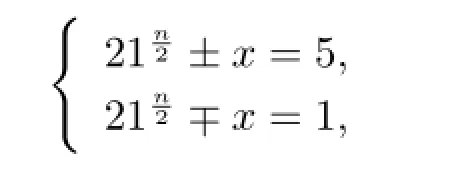
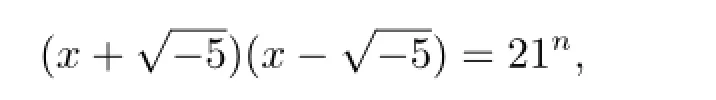
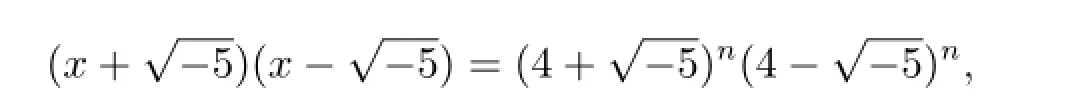
從而有

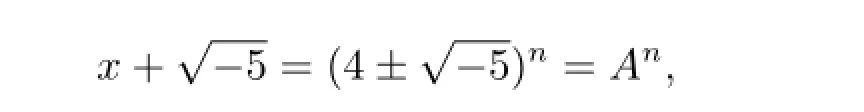
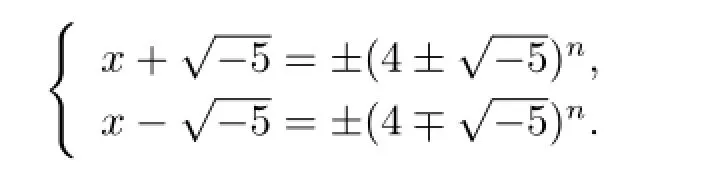
進而有

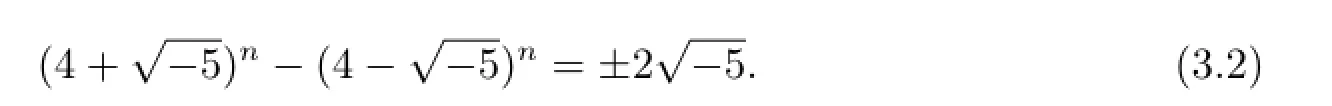
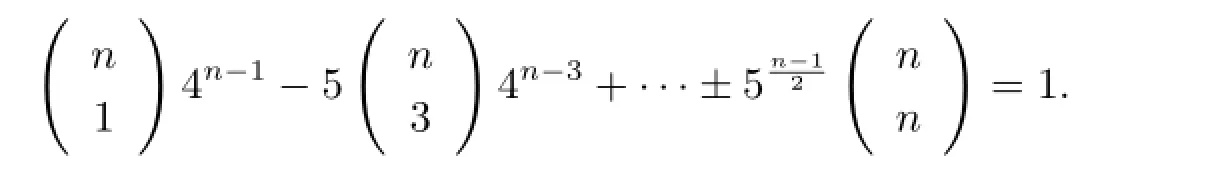
所以n·4n-1≡1（mod5）.故n·（-1）n-1≡1（mod5）.令f（n）≡n·（-1）n-1（mod5），由于其周期為10.即f（10n+k）≡f（k）（mod5）.故n≡1，4（mod10），又由條件n是奇數(shù)知n≡1（mod2），從而由定理1.1得n≡1（mod10）.當(dāng)n=1時，方程有正整數(shù)解（x，n）=（4，1）.

下證方程（3.1）的指數(shù)n不能有兩個不同的解n1和n2，滿足n1-n2≡0（mod10）.否則，可設(shè)

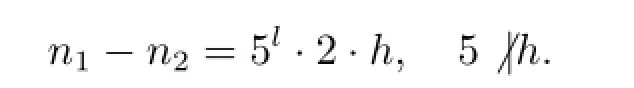
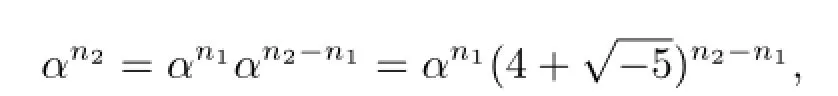
對于5l+1的方冪實行數(shù)學(xué)歸納法可證

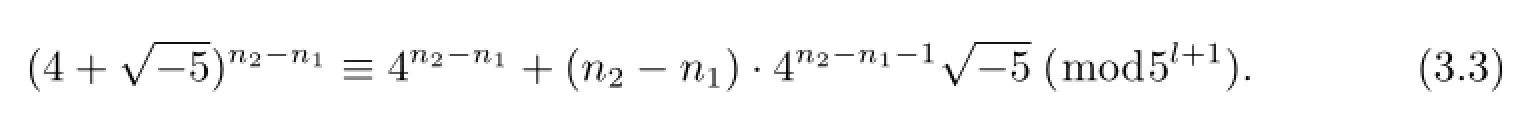
又因

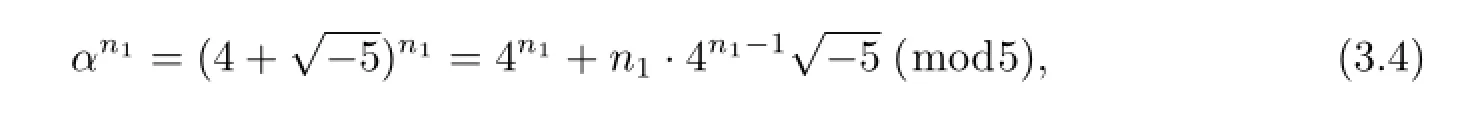
由（3.3）式和（3.4）式知

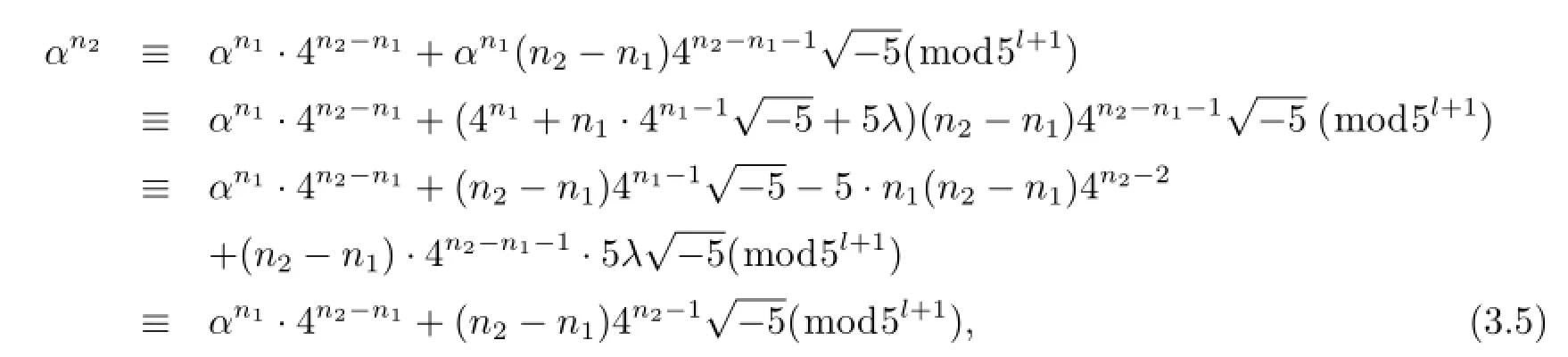
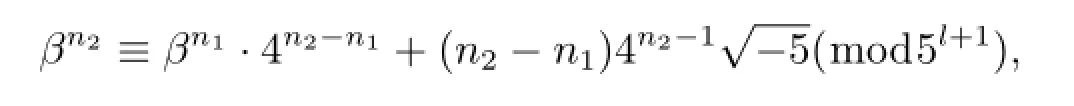
由于（3.2）式中的右端不能夠取負號，即αn1-βn1=αn2-βn2.故

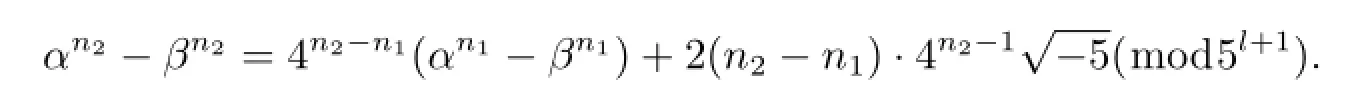
又因為n2-n1≡0（mod10），n1-1≡0（mod2），且4|n2-n1.即4n2-n1≡1（mod5）.所以有4n2-1≡±1（mod5）.故有

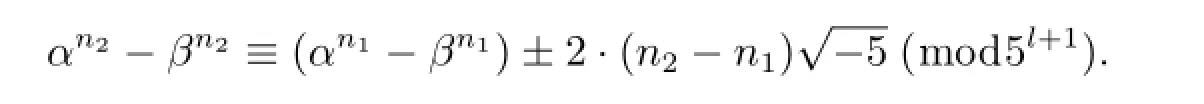
進而有

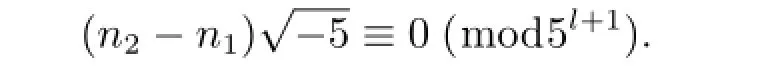
即

亦即

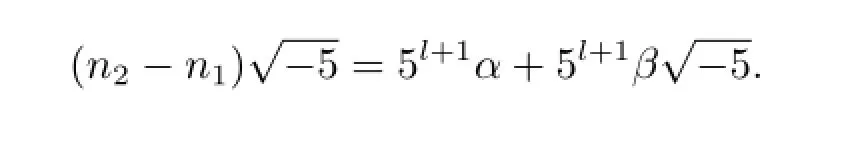
于是得

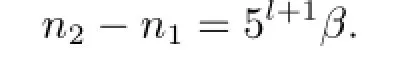
即n2-n1≡0（mod5l+1）.與5l/|n2-n1矛盾.故方程（3.1）的正整數(shù)解唯一，僅有（x，n）=（4，1），證畢.

［1］樂茂華.關(guān)于廣義Ramanujan-Nagell方程x2+D=pn的解數(shù)［J］.常德師范學(xué)院學(xué)報（自然科學(xué)版），2002，14（1）：1-2.

［2］曹珍富.丟番圖方程引論［M］.哈爾濱：哈爾濱工業(yè)大學(xué)出版社，2012.

［3］華羅庚.數(shù)論導(dǎo)引［M］.北京：科學(xué)出版社，1979.

［4］張禾瑞.近世代數(shù)基礎(chǔ)（修訂本）［M］.北京：高等教育出版社，2010.

［5］馮克勤.代數(shù)數(shù)論［M］.北京：科學(xué)出版社，2000.

［6］潘承洞，潘承彪.代數(shù)數(shù)論（第二版）［M］.濟南：山東大學(xué)出版社，2001.

［7］閔嗣鶴，嚴士健.初等數(shù)論（第三版）［M］.北京：高等教育出版社，2003.

［8］楊仕椿.廣義Ramanujan-Nagell方程x2+Dm=pn的解的注記［J］.數(shù)學(xué)學(xué)報，2007，50（4）：943-948.

［9］樂茂華.關(guān)于廣義Ramanujan-Nagell方程的一點注記［J］.數(shù)學(xué)雜志，2007，27（2）：219-221.

［10］楊繼明.廣義Ramanujan-Nagell方程x2-D=3n的解數(shù)［J］.數(shù)學(xué)學(xué)報，2008，51（2）：351-356.

［11］陳候炎.關(guān)于廣義Ramanujan-Nagell方程的一個猜想［J］.數(shù)學(xué)雜志，2010，50（4）：567-569.

［12］樂茂華，胡永忠.廣義Lebesgue-Ramanujan-Nagell方程研究的新進展［J］.數(shù)學(xué)進展，2012，41（4）：385-393.

ON THE POSITIVE INTEGER SOLUTIONS OF A CLASS OF GENERALIZED RAMANUJAN-NAGELL EQUATION

ZHANG Zheng-ping1，ZHAO Kai-ming2
（1.School of Mathematics and Physics，Chongqing University of Science and Technology，Chongqing 401331，China）
（2.Chongqing Refinement School，Chongqing 400015，China）

In this paper，we studied the necessary condition for existence of the positive integer solutions of a class of generalized Ramanujan-Nagell equation.On the base of it，we gave all the positive integer solutions of a typical Ramanujan-Nagell equations，and generalized some results of reference［1］and［2］.

generalized Ramanujan-Nagell equation；positive integer solution；quadratic fields

MR（2010）主題分類號：11D45；11D75O156.7

A

0255-7797（2016）05-1077-06

2014-10-08接收日期：2014-12-24

重慶市自然科學(xué)基金項目（cstc2013jcyjA10049）；重慶科技學(xué)院本科教育教學(xué)改革研究項目（201249）.

張正萍（1973-），女，四川瀘州，講師，研究方向：數(shù)論.

2010 MR Subject Classification：11D45；11D75