3×3階上三角算子矩陣的點(diǎn)譜和剩余譜擾動(dòng)

黃俊杰，吳秀峰，阿拉坦倉

（內(nèi)蒙古大學(xué)數(shù)學(xué)科學(xué)學(xué)院，內(nèi)蒙古呼和浩特010021）

3×3階上三角算子矩陣的點(diǎn)譜和剩余譜擾動(dòng)

黃俊杰，吳秀峰，阿拉坦倉

（內(nèi)蒙古大學(xué)數(shù)學(xué)科學(xué)學(xué)院，內(nèi)蒙古呼和浩特010021）

基于值域的稠密性和閉性，有界線性算子T的點(diǎn)譜和剩余譜可分別細(xì)分為σp，1（T），σp，2（T）和σr，1（T），σr，2（T）.設(shè)H1，H2，H3為無窮維復(fù)可分Hilbert空間，給定A∈B（H1），B∈B（H2），C∈B（H3），結(jié)合分析方法與算子分塊技巧給出了MD，E，F(xiàn)的上述四種譜隨D，E，F(xiàn)擾動(dòng)的完全描述.

算子矩陣；點(diǎn)譜；剩余譜；擾動(dòng)

1　引言

缺少了某些元素的算子矩陣稱為缺項(xiàng)算子矩陣.算子矩陣的譜補(bǔ)問題旨在討論缺項(xiàng)算子矩陣中所缺的元素對整個(gè)算子矩陣譜的影響，在換位提升理論，插值理論，以及系統(tǒng)控制理論中具有重要應(yīng)用.算子矩陣的譜擾動(dòng)屬于譜補(bǔ)問題的研究范疇，它是當(dāng)所缺的元素跑遍特定的集合時(shí)整個(gè)算子矩陣譜的穩(wěn)定的組成部分.

設(shè)H1，H2，H3為無窮維復(fù)可分Hilbert空間.以B（Hi，Hj）表示從Hi到Hj的所有有界（線性）算子構(gòu)成的集合，B（Hi，Hi）簡記為B（Hi），其中i，j=1，2，3.給定A∈B（H1），B∈B（H2），C∈B（H3），記

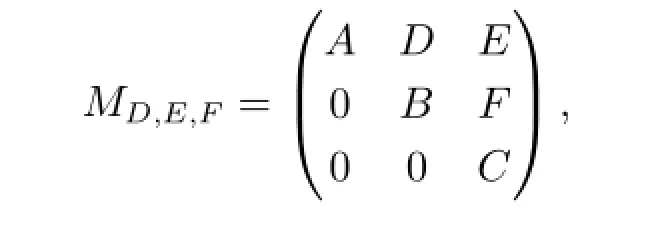
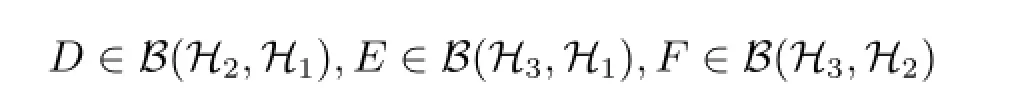
其中為待定的未知算子.顯然，MD，E，F(xiàn)是H1⊕H2⊕H3上的缺項(xiàng)上三角算子矩陣.為敘述方便，對于給定算子A∈B（H1），B∈B（H2），以MD表示缺項(xiàng)2×2階上三角算子矩陣

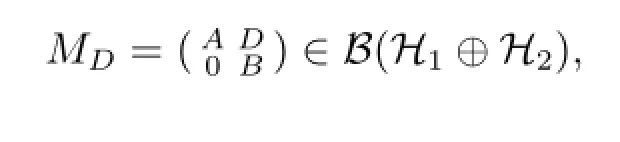
其中D∈B（H2，H1）待定.

經(jīng)過近二十年的積累，2×2階上三角算子矩陣的譜擾動(dòng)研究已日臻完善，涌現(xiàn)出諸如譜，點(diǎn)譜，剩余譜，連續(xù)譜，近似點(diǎn)譜，虧譜，本質(zhì)譜，Weyl譜，以及Browder譜等的擾動(dòng)結(jié)果［2，3，5-8，10-18］.例如，文［15］研究了上三角算子矩陣MD的點(diǎn)譜和剩余譜擾動(dòng)，得到如下結(jié)果

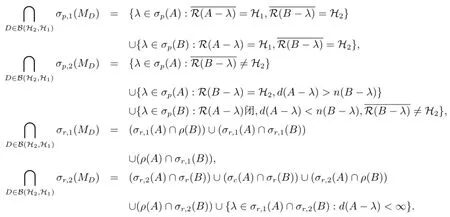
最近，文［4，18］分別研究了上三角算子矩陣MD，E，F(xiàn)的左（右）本質(zhì)譜，以及點(diǎn)譜，剩余譜和連續(xù)譜的擾動(dòng)；文［9］給出了MD，E，F(xiàn)的點(diǎn)譜，連續(xù)譜和剩余譜之并集的描述.本文在文［15］的基礎(chǔ)上探討了3×3階情形，得到

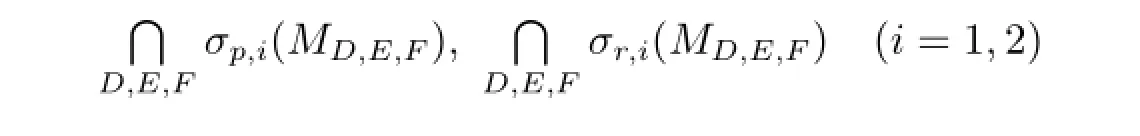
的完全描述.

對于有界算子T，分別以T?，N（T）和R（T）表示T的共軛算子，零空間和值域；以n（T），d（T）分別表示N（T），N（T?）的維數(shù)，即n（T）=dimN（T），d（T）=dimN（T?）.下面給出文中涉及的一些基本概念和輔助引理.

定義1.1［1］設(shè)T為Banach空間X中的有界線性算子，則T的預(yù)解集ρ（T）定義為

ρ（T）=｛λ∈C：T-λ具有定義于X上的有界逆｝，并稱集合σ（T）=Cρ（T）為T的譜.

由閉圖象定理，λ∈ρ（T）當(dāng)且僅當(dāng)T-λ是雙射.顯然，σ（T）可分成下述互不相交的組成部分σ（T）=σp（T）∪σr（T）∪σc（T），其中

分別為T的點(diǎn)譜，剩余譜和連續(xù)譜.類似于文［1］，可對點(diǎn)譜和剩余譜進(jìn)一步細(xì)分為

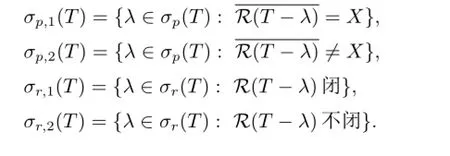
此外，稱集合

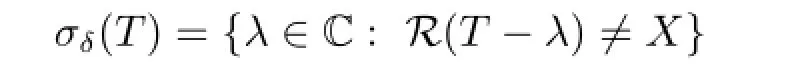
為T的虧譜.為敘述方便，記

如所熟知，λ∈ρm（T）當(dāng)且僅當(dāng)R（T-λ）閉；λ∈ρl（T）當(dāng)且僅當(dāng)T-λ為具有閉值域的單射.顯然，σp，1（T）=σp（T）∩ρco（T），σp，2（T）=σp（T）∩σco（T），σr，1（T）=σr（T）∩ρm（T），σr，2（T）=σr（T）∩σm（T）.

引理1.1［9］設(shè)X，Y為Banach空間，T∈B（X，Y）.若R（T）不閉，則存在無窮維子空間使得

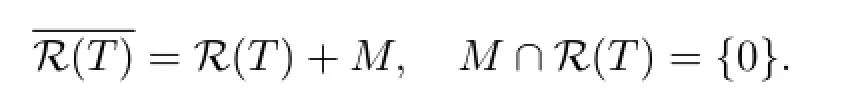
引理1.2設(shè)X，Y為Banach空間，T∈B（X，Y）.下述結(jié)論顯然成立.

（i）若S∈B（X，Y）為有限秩算子，則R（T）閉當(dāng)且僅當(dāng)R（T+S）閉；

（ii）若U∈B（Y），V∈B（X）為可逆算子，則R（T）閉當(dāng)且僅當(dāng)R（UTV）閉.

引理1.3設(shè)A∈B（H1），B∈B（H2），C∈B（H3）為給定算子，則任給D，E，F(xiàn)均有λ∈ρin（MD，E，F(xiàn)）的充要條件為λ∈ρin（A）∩ρin（B）∩ρin（C）.

引理1.4設(shè)A∈B（H1），B∈B（H2），C∈B（H3）為給定算子，則任給D，E，F(xiàn)均有λ∈ρco（MD，E，F(xiàn)）的充要條件為λ∈ρco（A）∩ρco（B）∩ρco（C）.

引理1.1的證明見［9，推論1］；引理1.2是熟知的，引理1.3，1.4是顯然的，證明從略.

2　主要結(jié)論及其證明

本節(jié)給出本文的主要結(jié)果和證明.為便于敘述，以下記

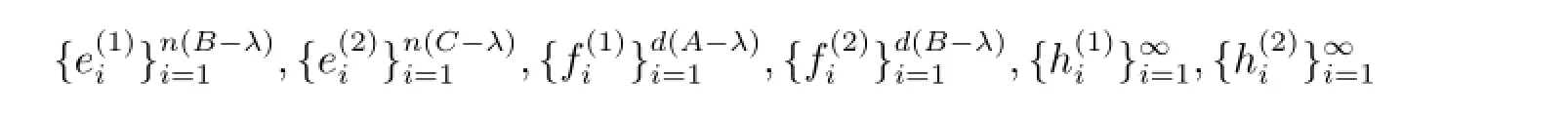
分別為N（B-λ），N（C-λ），R（A-λ）⊥，R（B-λ）⊥，H1，H2的規(guī)范正交基，其中A∈B（H1），B∈B（H2），C∈B（H3）.

定理2.1設(shè)A∈B（H1），B∈B（H2），C∈B（H3）為給定算子，則

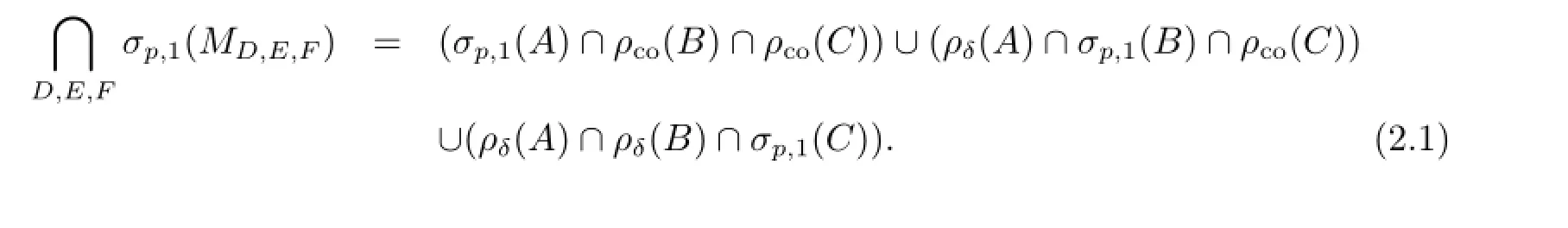
若λ∈Σ1，則λ∈σp（A），顯然任給D，E，F(xiàn)均有λ∈σp（MD，E，F(xiàn)）.若λ∈Σ2Σ1，則λ∈ρ（A）∩σp，1（B）∩ρco（C），所以任給D，E，F(xiàn)均存在可逆算子V使得

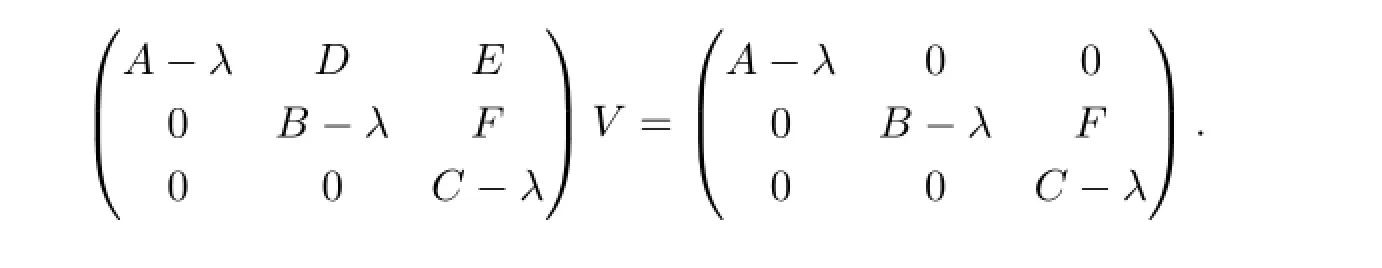
注意到λ∈σp（B）和V的可逆性，顯然任給D，E，F(xiàn)均有λ∈σp（MD，E，F(xiàn)）.若λ∈Σ3（Σ1∪Σ2），則λ∈ρ（A）∩ρ（B）∩σp，1（C），同上討論即可，不再贅述.

下面證明Σ?Σ1∪Σ2∪Σ3.為此，只須證若λ/∈Σ1∪Σ2∪Σ3必有λ/∈Σ，可分以下4種情形討論.

情形1 λ∈σco（A）∪σco（B）∪σco（C）.此時(shí)，取D，E，F(xiàn)均為零算子，顯然= H1⊕H2⊕H3，因此λ/∈Σ.

情形2 λ∈ρco（A）∩ρco（B）∩ρco（C）∩ρin（A）∩σm（A）.此時(shí)，由引理1.1，存在無窮維子空間M使得M∩R（A-λ）=｛0｝.記M的某個(gè)含有無窮多元素的規(guī)范正交集為.定義F=0，

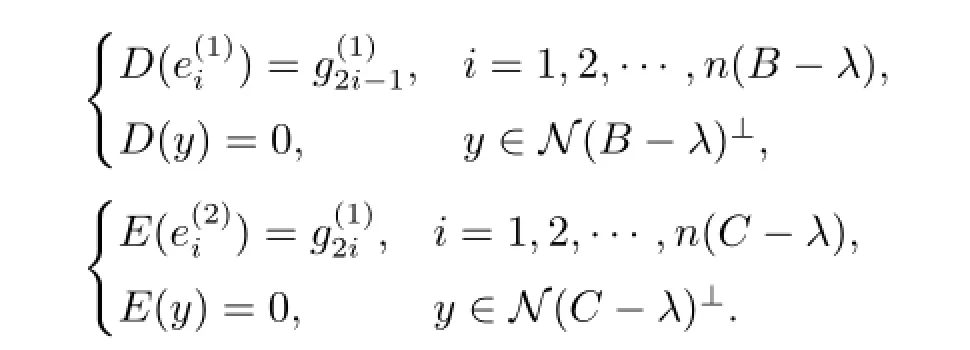
則MD，E，F(xiàn)-λ為單射，顯然λ/∈Σ.

情形3 λ∈ρco（A∩ρco（C）∩ρin（A）∩ρin（B）∩σm（B）.此時(shí)，類似于情形2，存在無窮維子空間N?R（B-λ）使得N∩R（B-λ）=｛0｝.記N的某個(gè)含有無窮多元素的規(guī)范正交集為.取D，E均為零算子，并定義

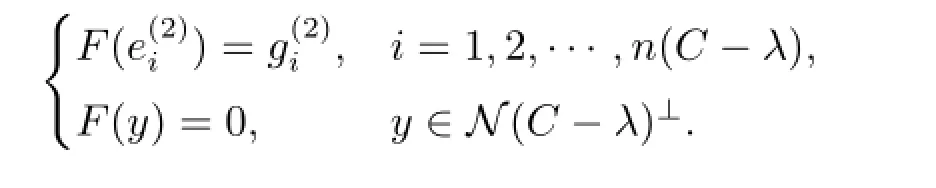
顯然MD，E，F(xiàn)-λ為單射，因此λ/∈Σ.

情形4 λ∈ρco（A）∩ρco（B）∩ρco（C）∩ρin（A）∩ρin（B）∩ρin（C）.此時(shí)，由引理1.3，取D，E，F(xiàn)均為零算子便有MD，E，F(xiàn)-λ為單射，因此λ/∈Σ.

定理2.2設(shè)A∈B（H1），B∈B（H2），C∈B（H3）為給定算子，則

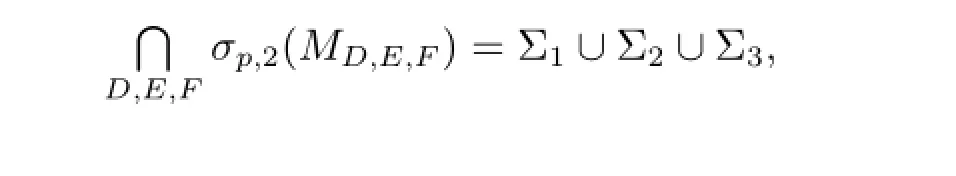
其中

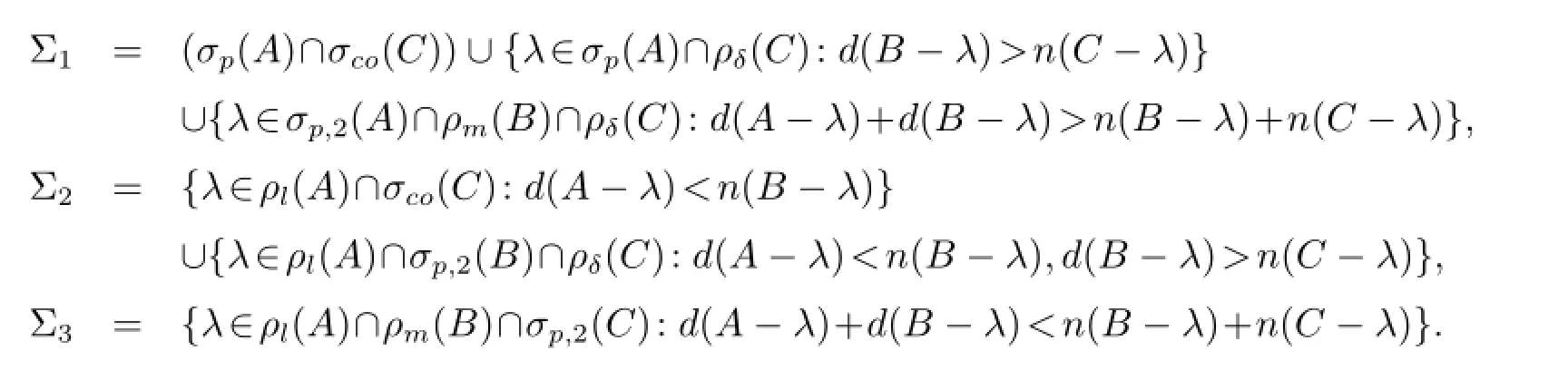
若λ∈Σ11，則λ∈σp（A）且/=H3.顯然λ∈Σ.現(xiàn)設(shè)λ∈Σ12.由λ∈ρδ（C）可知任給D，E，F(xiàn)算子矩陣MD，E，F(xiàn)-λ均有如下分塊表示

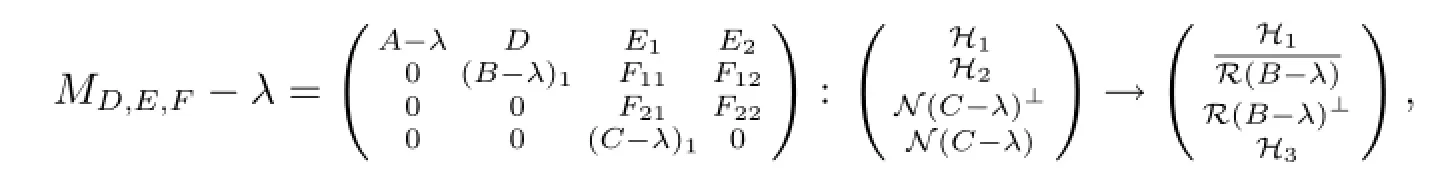
其中（C-λ）1為可逆算子.因此存在可逆算子U使得

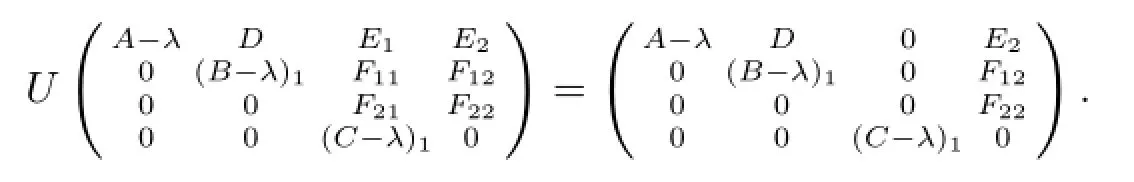
注意到d（B-λ）＞n（C-λ）可知無論如何選取D，E，F(xiàn)均有F22具有閉值域且不是滿射，進(jìn)而由U的可逆性得到λ∈σco（MD，E，F(xiàn)）.再由λ∈σp（A），顯然λ∈Σ.以下假設(shè)λ∈Σ13.由于λ∈ρδ（C）∩ρm（B），所以任給D，E，F(xiàn)均有

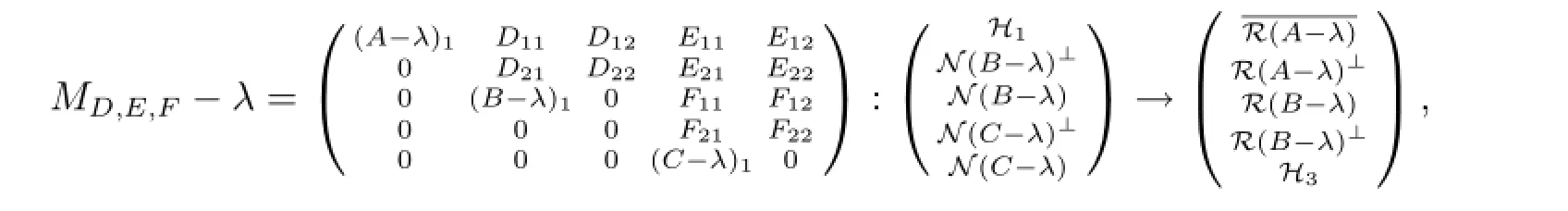
其中（B-λ）1，（C-λ）1為可逆算子.因此存在可逆算子U使得

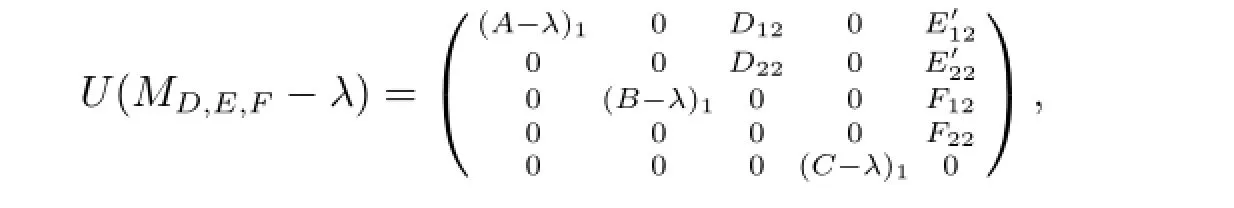
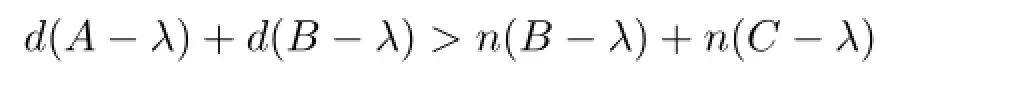
設(shè)λ∈Σ2.由于λ∈ρl（A），所以任給D，E，F(xiàn)均有

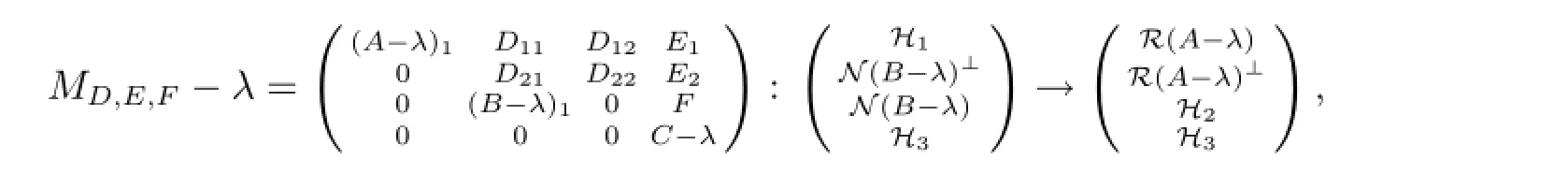
其中（A-λ）1為可逆算子.因此存在可逆算子V使得

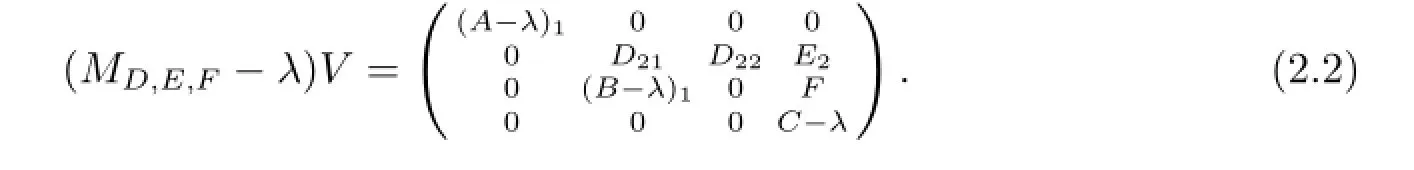
注意到n（B-λ）＞d（A-λ），顯然無論如何選取D，E，F(xiàn)均有D22不是單射，進(jìn)而由式（2.2）便知λ∈σp（MD，E，F(xiàn)）.這樣，若λ∈σco（C），則任給D，E，F(xiàn)均有λ∈σco（MD，E，F(xiàn)），顯然λ∈Σ；若λ∈ρδ（C）且d（B-λ）＞n（C-λ），則由Σ12的證明可知任給D，E，F(xiàn)均有λ∈σco（MD，E，F(xiàn)），從而λ∈Σ.于是Σ?Σ2.

現(xiàn)設(shè)λ∈Σ3.由λ∈ρl（A）∩ρm（B）可知任給D，E，F(xiàn)均有

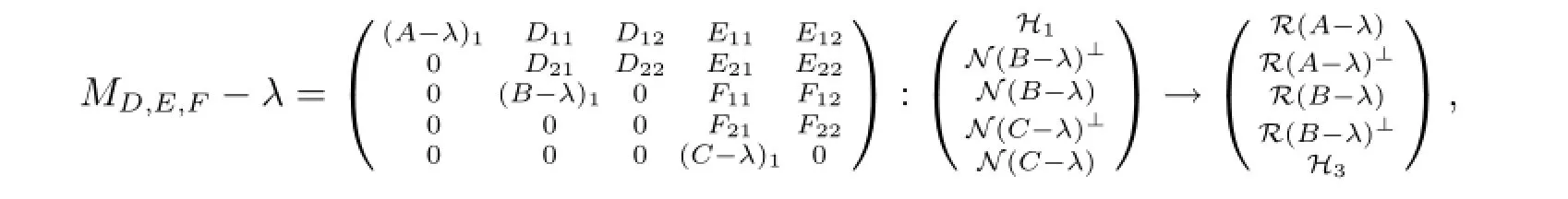
其中（A-λ）1，（B-λ）1均為可逆算子，（C-λ）1為單射.因此存在可逆算子U，V使得

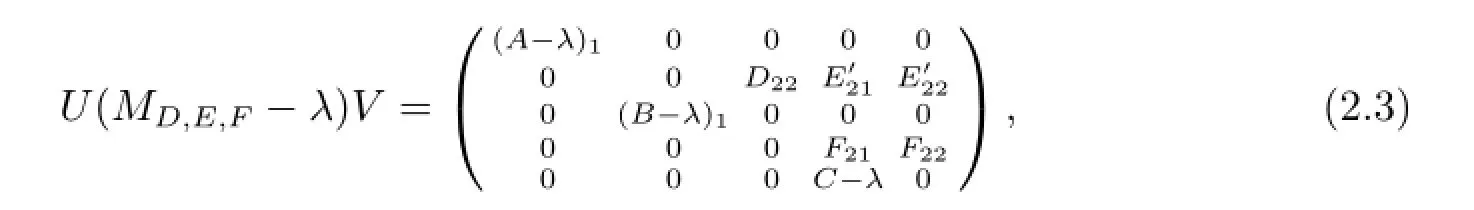
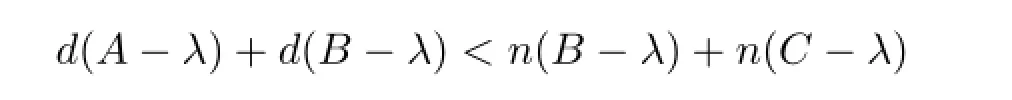
下面證明相反的包含關(guān)系.為此只須證若λ/∈Σ1∪Σ2∪Σ3必有λ/∈Σ，可分以下6種情形討論.

情形1 λ∈ρin（A）∩σm（A）.此時(shí)，取定理2.1中情形2的D，E，F(xiàn)便有MD，E，F(xiàn)-λ為單射，因此λ/∈Σ.

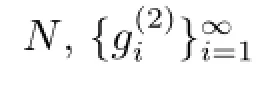
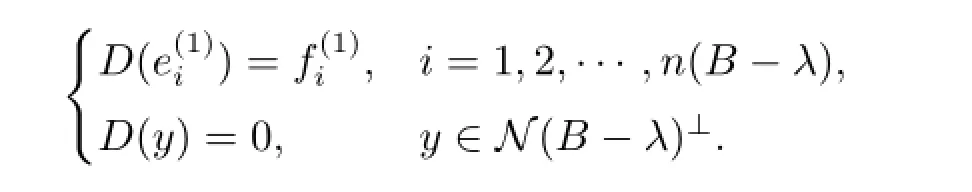
則MD，E，F(xiàn)-λ為單射，顯然λ/∈Σ.

情形3 λ∈ρl（A）∩ρm（B），d（A-λ）≥n（B-λ）且d（A-λ）+d（B-λ）≥n（B-λ）+ n（C-λ）.此時(shí)，定義

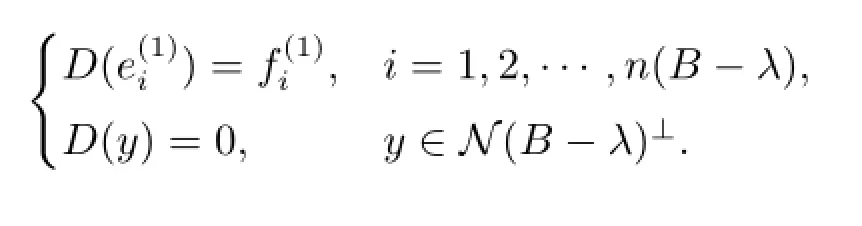
若d（B-λ）≥n（C-λ），則定義E=0，

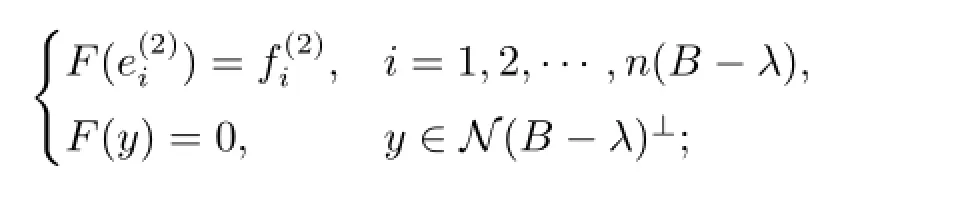
若d（B-λ）＜n（C-λ），由d（A-λ）+d（B-λ）≥n（B-λ）+n（C-λ）可知

則定義

容易驗(yàn)證MD，E，F(xiàn)-λ為單射，顯然λ/∈Σ.

情形4 λ∈ρco（C）∩σm（C）.此時(shí)，注意到λ∈σm（C）當(dāng)且僅當(dāng).由引理1.1，存在無窮維子空間=N（C-λ）⊥使得=｛0｝.記Z的某個(gè)含有無窮多元素的規(guī)范正交集為.定義D=0，

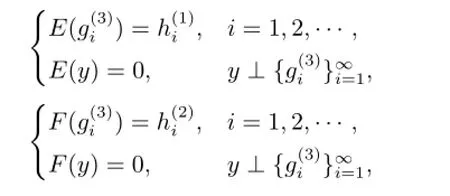
則E?∈B（H1，H3），F(xiàn)?∈B（H2，H3）均為單射，而且R（E?）=R（F?）=：i= 1，2，···｝.注意到=｛0｝和λ∈ρco（C），所以立即得到是單射.即 MD，E，F(xiàn)-λ具有稠值域，從而λ/∈Σ.

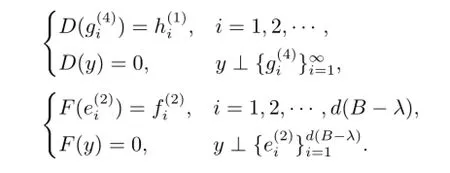
顯然，MD，E，F(xiàn)-λ具有稠值域，因此λ/∈Σ.

情形6 λ∈ρm（B）∩ρδ（C），d（B-λ）≤n（C-λ）且d（A-λ）+d（B-λ）≤n（B-λ）+ n（C-λ）.此時(shí)，定義

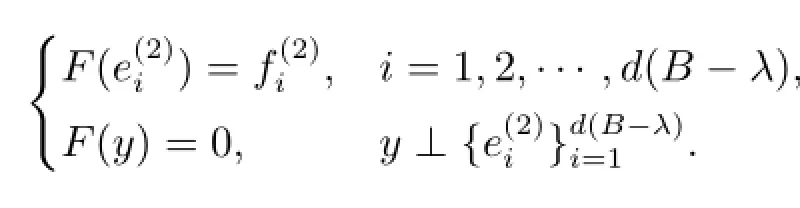
若d（A-λ）≤n（B-λ），則定義E=0，

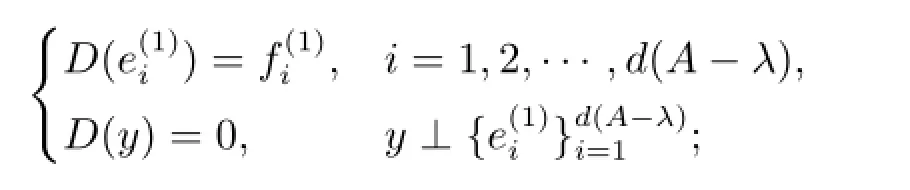
否則注意到d（A-λ）-n（B-λ）≤n（C-λ）-d（B-λ），定義

不難看出MD，E，F(xiàn)-λ是滿射，從而λ/∈Σ.

定理2.3設(shè)A∈B（H1），B∈B（H2），C∈B（H3）為給定算子，則

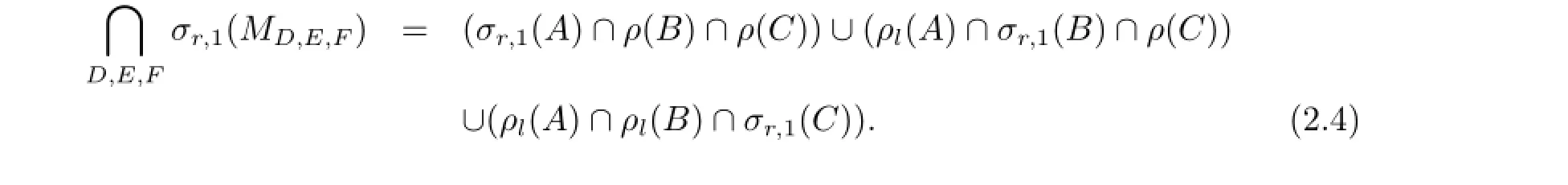
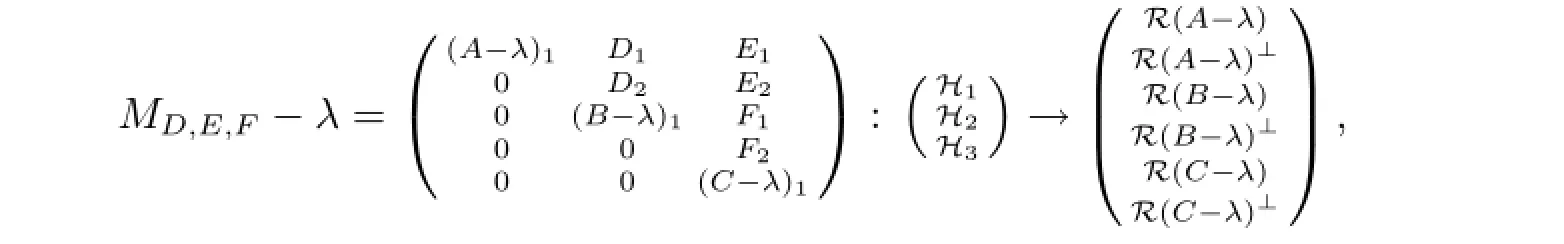
其中（A-λ）1，（B-λ）1，（C-λ）1均為可逆算子.因此存在可逆算子U使得

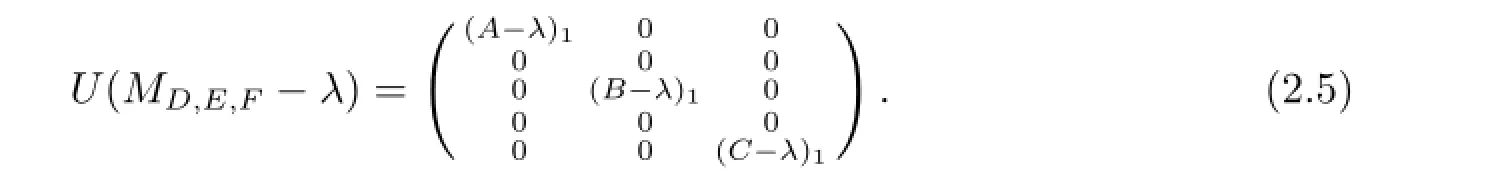
注意到d（A-λ），d（B-λ），d（C-λ）至少有一個(gè)大于零，由式（2.5）可知無論如何選取D，E，F(xiàn)均有MD，E，F(xiàn)-λ左可逆且R（MD，E，F(xiàn)-λ）/=H1⊕H2⊕H3.因此λ∈Σ.于是Σ?Σ1∪Σ2∪Σ3.

再證相反的包含關(guān)系.本文斷言：λ∈Σ蘊(yùn)含λ∈ρl（A）∩ρl（B）∩ρl（C）.若不然，取D，E，F(xiàn)皆為零算子便有λ∈σl（MD，E，F(xiàn)），這與λ∈Σ矛盾.因此只須證若λ∈（ρl（A）∩ρl（B）∩ρl（C））（Σ1∪Σ2∪Σ3）便有λ/∈Σ.這是顯然的，因?yàn)棣恕师?∪Σ2∪Σ3蘊(yùn)含λ∈ρl（A）∩ρl（B）∩ρl（C）且A-λ，B-λ，C-λ至少有一個(gè)值域不稠，從而若λ∈（ρl（A）∩ρl（B）∩ρl（C））（Σ1∪Σ2∪Σ3）便有λ∈ρ（A）∩ρ（B）∩ρ（C）.

定理2.4設(shè)A∈B（H1），B∈B（H2），C∈B（H3）為給定算子，則

其中

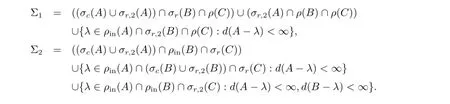
現(xiàn)記Σi的表達(dá)式中等號(hào)右端的集合依次為Σi1，Σi2，Σi3（i=1，2）.若λ∈Σ11∪Σ12∪Σ21，則必有λ∈σm（A）.顯然任給D，E，F(xiàn)均有λ∈σm（MD，E，F(xiàn)）.若λ∈Σ13，則任給D，E，F(xiàn)均有

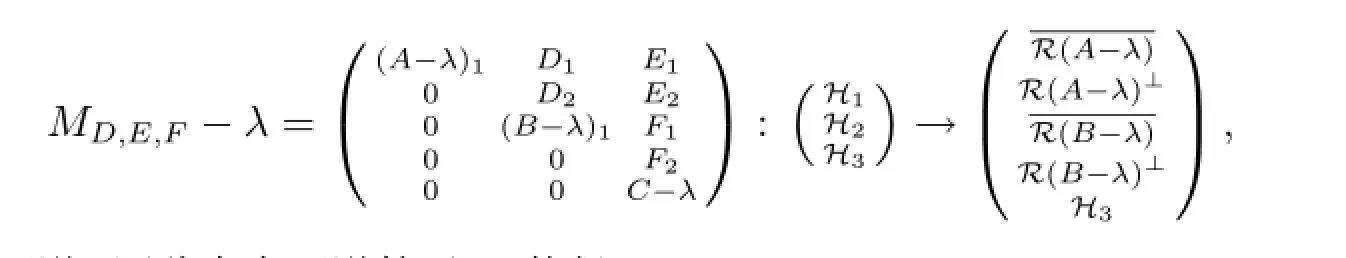
其中C-λ可逆.因此存在可逆算子U使得

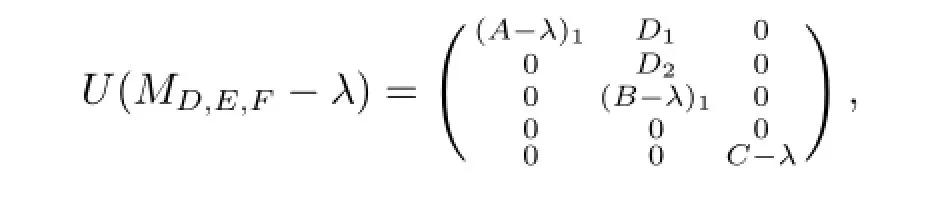
結(jié)合d（A-λ）＜∞，應(yīng)用引理1.2可有λ∈σm（MD，E，F(xiàn)）當(dāng)且僅當(dāng)

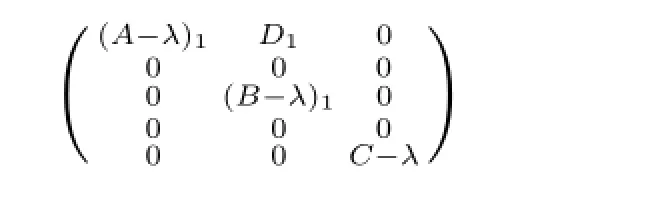
的值域不閉.這樣若λ∈σm（A），同前述討論可知，任給D，E，F(xiàn)均有λ∈σm（MD，E，F(xiàn)）；若λ/∈σm（A），則（A-λ）1為可逆算子，注意到λ∈σr，2（B）容易得到任給D，E，F(xiàn)均有λ∈σm（MD，E，F(xiàn)）.類似地，容易證明若λ∈Σ22∪Σ23，則任給D，E，F(xiàn)仍有λ∈σm（MD，E，F(xiàn)）.

再證Σ?Σ1∪Σ2.注意到任給D，E，F(xiàn)均有σr，2（MD，E，F(xiàn)）?σm（MD，E，F(xiàn)）.所以要證λ/∈Σ1∪Σ2蘊(yùn)含λ/∈Σ，只須考慮如下3種情形即可.

情形1 λ∈σc（C），d（A-λ）＜∞且d（B-λ）＜∞.此時(shí)，注意到λ∈σm（C），取形如定理2.2中情形4的D，E，F(xiàn)可知MD，E，F(xiàn)-λ具有稠值域，顯然λ/∈Σ.

情形2 λ∈σr，1（A）∩σc（B）∩ρ（C）且d（A-λ）＜∞.此時(shí)，取E，F(xiàn)均為零算子并定義，顯然MD，E，F(xiàn)-λ具有稠值域，從而λ/∈Σ.

情形3 λ∈（ρ（A）∩σc（B）∩ρ（C））∪（σc（A）∩（ρ（B）∪σc（B））∩ρ（C））∪（σc（A）∩σc（B）∩ρ（C））.此時(shí)，取D，E，F(xiàn)均為零算子，顯然MD，E，F(xiàn)-λ具有稠值域，因此λ/∈Σ.

注由上述定理，文［15］的結(jié)果可描述為

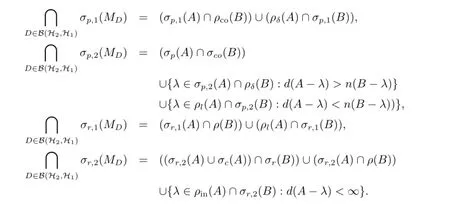
［1］Azizov T Ya，Iokhvidov I S.Linear operators in spaces with an indefinite metric［M］.Chichester：John Wiley&Sons Ltd.，1989.

［2］Cao X，Meng B.Essential approximate point spectra and Weyl's theorem for operator matrices［J］. J.Math.Anal.Appl.，2005，304：759-771.

［3］Cao X.Browder essential approximate point spectra and hypercyclicity for operator matrices［J］. Lin.Alg.Appl.，2007，426：317-324.

［4］曹小紅.3×3階上三角算子矩陣的Weyl型定理［J］.數(shù)學(xué)學(xué)報(bào)（中文版），2006，49：529-538.

［5］Djordjevi′c D S.Perturbations of spectra of operator matrices［J］.J.Oper.The.，2002，48：467-486.

［6］Djordjevi′c S V，Zguitti H.Essential point spectra of operator matrices through local spectral theory［J］.J.Math.Anal.Appl.，2008，338：285-291.

［7］Du H，Pan J.Perturbation of spectrums of 2×2 operator matrices［J］.Proc.Amer.Math.Soc.，1994，121：761-766.

［8］Hai G.，Chen A.On the right（left）invertible completions for operator matrices［J］.Integr.Equ. Oper.The.，2010，67：79-93.

［9］Hai G，Alatancang.Possible spectrums of 3×3 upper triangular operator matrices［J］.J.Math.Res. Expo.，2009，29：649-661.

［10］黃俊杰，阿拉坦倉，王華.上三角算子矩陣譜的自伴擾動(dòng)［J］.數(shù)學(xué)學(xué)報(bào)（中文版），2010，53：1193-1200.

［11］Hwang I S，Lee W Y.The boundedness below of 2×2 upper triangular operator matrices［J］.Integr. Equ.Oper.The.，2001，39：267-276.

［12］Li Y，Du H.The intersection of essential approximate point spectra of operator matrices［J］.J.Math. Anal.Appl.，2006，323：1171-1183.

［13］Li Y，Sun X，Du H.The intersection of left（right）spectra of 2×2 upper triangular operator matrices［J］.Lin.Algebra Appl.，2006，418：112-121.

［14］Zerouali E H，Zguitti H.Perturbation of spectra of operator matrices and local spectral theory［J］. J.Math.Anal.Appl.，2006，324：992-1005.

［15］張瀾，阿拉坦倉.一類缺項(xiàng)算子矩陣的譜擾動(dòng)［J］.應(yīng)用數(shù)學(xué)學(xué)報(bào)，2010，33：59-65.

［16］Zhang H，Du H.Browder spectra of upper-triangular operator matrices［J］.J.Math.Anal.Appl.，2006，323：700-707.

［17］Zhang S，Wu Z，Zhong H.Continuous spectrum，point spectrum and residual spectrum of operator matrices［J］.Lin.Algebra Appl.，2010，433：653-661.

［18］吳秀峰，黃俊杰，阿拉坦倉.三階上三角算子矩陣點(diǎn)譜，連續(xù)譜和剩余譜的擾動(dòng)［J］.數(shù)學(xué)學(xué)報(bào)，2015，35（3）：423-430.

PERTURBATION OF THE POINT AND RESIDUAL SPECTRA OF 3×3 UPPER TRIANGULAR OPERATOR MATRICES

HUANG Jun-jie，WU Xiu-feng，Alatancang
（School of Mathematical Sciences，Inner Mongolia University，Hohhot 010021，China）

The point and residual spectra of a bounded operator T are，respectively，split into σp，1（T），σp，2（T）and σr，1（T），σr，2（T），based on the denseness and closedness of its range. Let H1，H2，H3be infinite dimensional complex separable Hilbert spaces.Given the operators A∈B（H1），B∈B（H2）and C∈B（H3），some complete characterizations on the perturbations of the previous four spectra for the partial operator matrix MD，E，F(xiàn)are given by means of the analysis method and block operator technique.

operator matrix；point spectrum；residual spectrum；perturbation

MR（2010）主題分類號(hào)：47A10；47A55O177.1；O177.7

A

0255-7797（2016）05-1056-11

2014-04-11接收日期：2014-06-23

國家自然科學(xué)基金資助（11461049；11371185）；內(nèi)蒙古自治區(qū)自然科學(xué)基金資助（2013JQ01）.作者簡介：黃俊杰（1977-），男，蒙古族，內(nèi)蒙古興安盟，教授，主要研究方向：算子矩陣?yán)碚摷皯?yīng)用.

2010 MR Subject Classification：47A10；47A55