幾種廣義非線性發(fā)展方程的新解

李寧，套格圖桑

(內(nèi)蒙古師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院，內(nèi)蒙古呼和浩特010022）

幾種廣義非線性發(fā)展方程的新解

李寧，套格圖桑

(內(nèi)蒙古師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院，內(nèi)蒙古呼和浩特010022）

本文研究了構(gòu)造了廣義KdV方程和廣義KP-Burgers方程等幾種廣義非線性發(fā)展方程的新解的問題.利用三種輔助方程及其新解，獲得了廣義KdV方程和廣義KP-Burgers方程等幾種廣義非線性發(fā)展方程的新解.這些解由雙曲余割函數(shù)、雙曲正切函數(shù)、雙曲正割函數(shù)、雙曲余切函數(shù)和余割函數(shù)組成.

輔助方程；廣義KdV方程；廣義KP-Burgers方程

1　引言

眾所周知非線性波動問題是有許多物理問題做背景的.非線性發(fā)展方程是研究此類物理問題的重要數(shù)學(xué)模型，而非線性發(fā)展方程的求解等相關(guān)問題是孤立子理論的重要研究內(nèi)容之一.所以研究非線性發(fā)展方程的求解方法等問題具有重要的研究意義.

文獻(xiàn)［9］主要研究了如下幾個具任意次非線性項(xiàng)發(fā)展方程的求解問題，并獲得了新解.

廣義KdV方程

廣義Zakharv-Kuznetsov（ZK）方程

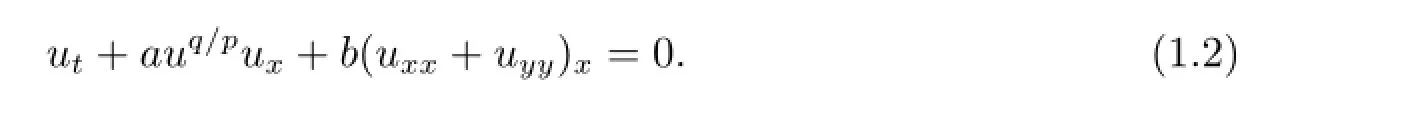
廣義Burgers方程

廣義KP-Burgers方程

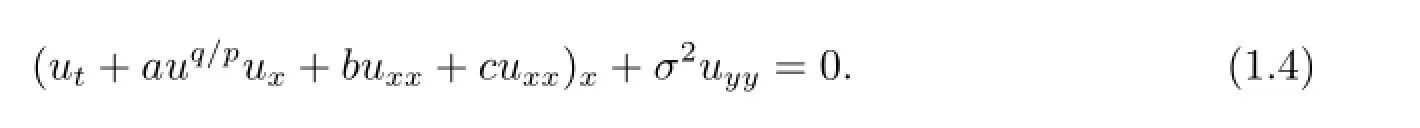
廣義ZK-Burgers方程

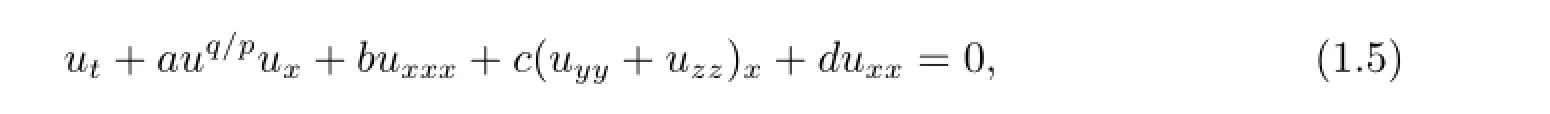
這里p和q都是任意的正整數(shù).

當(dāng)p=q時，方程（1.1）-（1.5）化為KdV方程，ZK方程，Burgers方程，KP-Burgers方程和ZK-Burgers方程，文獻(xiàn)［1-8］都研究過這些方程的求解問題，獲得了成果.

當(dāng)q=nq且n是整數(shù)（n≥1）時，方程（1.1）-（1.5）變成正整數(shù)冪的非線性發(fā)展方程.

文獻(xiàn)［9］利用如下兩個常微分方程，構(gòu)造了非線性常微分方程（1.1）-（1.5）的新解，

其解由雙曲正割函數(shù)和雙曲正切函數(shù)組成，形式分別如下

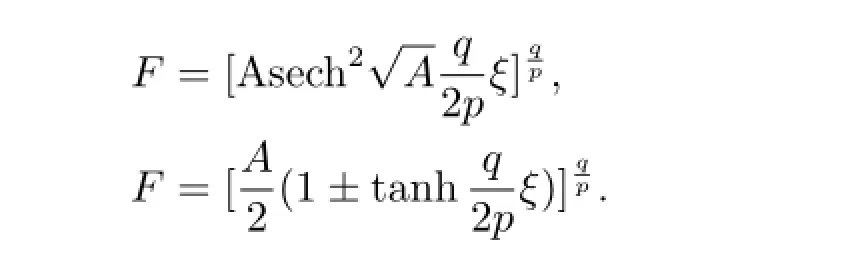
本文給出了包含常微分方程（1.6）和（1.7）的如下常微分方程，并獲得了新解，

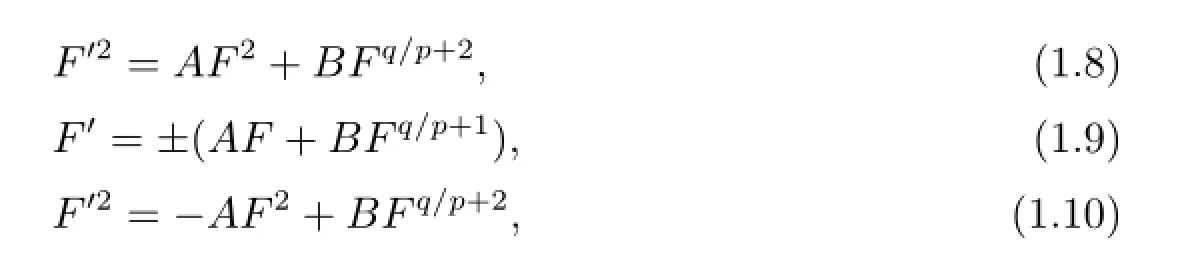
這里A＞0，p，q是正整數(shù)，B是常數(shù)，且當(dāng)B=-1時，方程（1.6）和（1.7）是方程（1.8）和（1.9）的特殊情況.

本文用方程（1.8），（1.9）和（1.10），構(gòu)造了廣義KdV方程和廣義KP-Burgers方程等幾種廣義非線性發(fā)展方程的新解.這些解由雙曲余割函數(shù)、雙曲正切函數(shù)、雙曲正割函數(shù)、雙曲余切函數(shù)和余割函數(shù)組成.

2　方法的介紹

考慮如下非線性發(fā)展方程

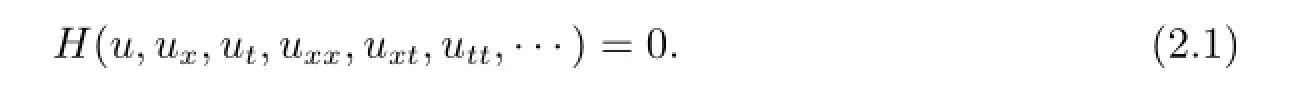
假設(shè)方程（2.1）的形式解為

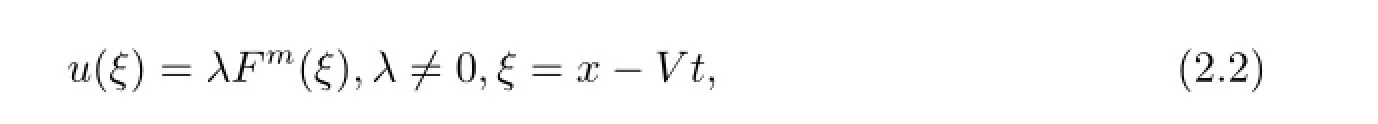
其中λ，V和m是待定系數(shù)，F(xiàn)=F（ξ）由常微分方程（1.8），（1.9）或（1.10）來確定.

經(jīng)計(jì)算獲得了常微分方程（1.8），（1.9）或（1.10）的如下新解：

常微分方程（1.8）的解為

這里A＞0，p，q是正整數(shù).

常微分方程（1.9）的解為

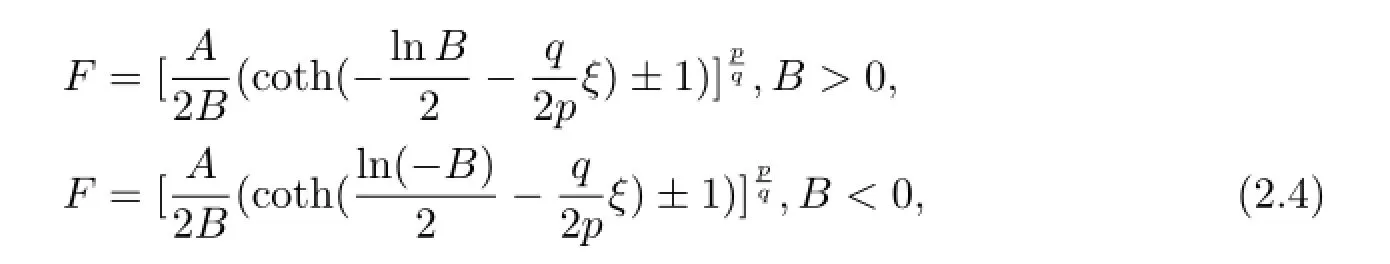
這里A＞0，p，q是正整數(shù).

常微分方程（1.10）的解為

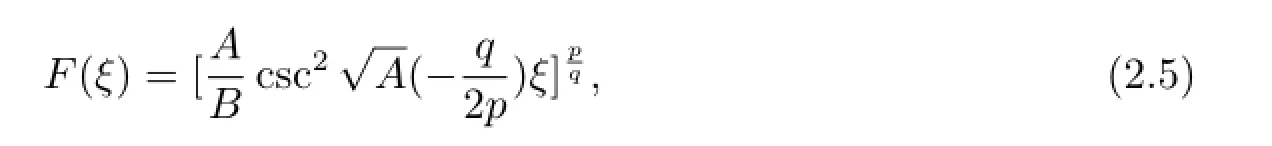
這里A＞0，p，q是正整數(shù).

將（2.2）式代入非線性發(fā)展方程（2.1），并利用齊次平衡法確定常數(shù)m.再令λFiF＇j（i，j≥0）的系數(shù)為零后得到一個以λ，V和A未知量的非線性代數(shù)方程組.解出λ，V和A，并與常微分方程的解F=F（ξ）一起代入形式解（2.2）后即可得到非線性發(fā)展方程（2.1）的新解.

3　幾種廣義非線性發(fā)展方程的新解

例1廣義KdV方程的解

把u（x，t）=u（ξ），ξ=x-V t（其中V是待定的常數(shù)）代入方程（1.1）后得

根據(jù)齊次平衡法，獲得如下方程

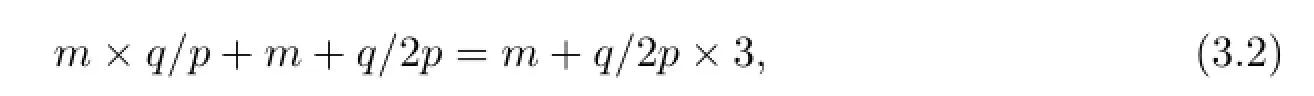
解出m=1.所以假設(shè)方程（1.1）的形式解為

情況1用常微分方程（1.8）構(gòu)造新解.

將（3.3）式和常微分方程（1.8）一起代入方程（3.1）得

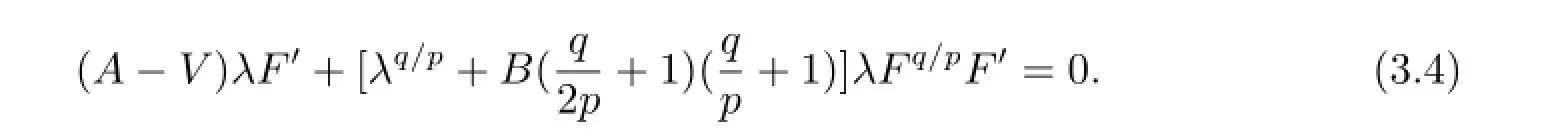
令λF＇，λFq/pF＇的系數(shù)為零，可以得到

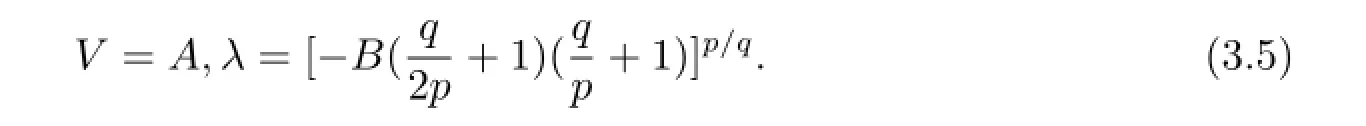
將（2.3）和（3.5）式代入（3.3）式可得到廣義KdV方程的如下解

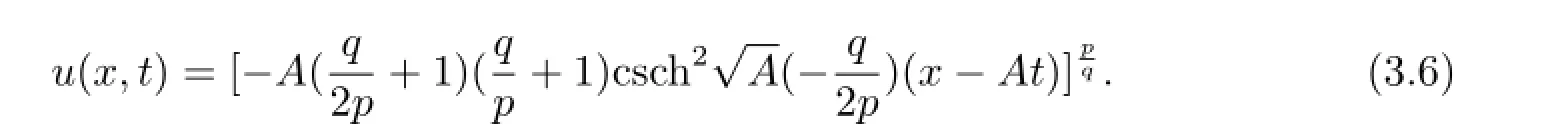
情況2用常微分方程（1.10）構(gòu)造新解.

將（3.3）式和常微分方程（1.10）一起代入方程（3.1）得

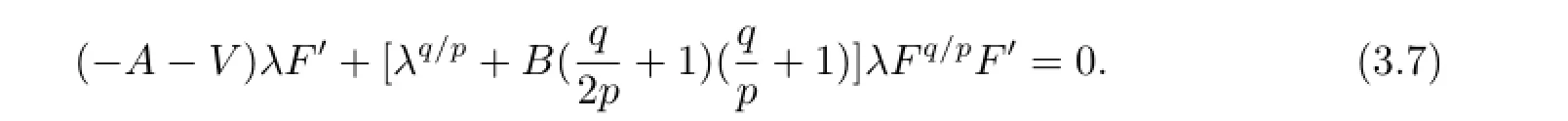
令λF＇，λFq/pF＇的系數(shù)為零，可以得到

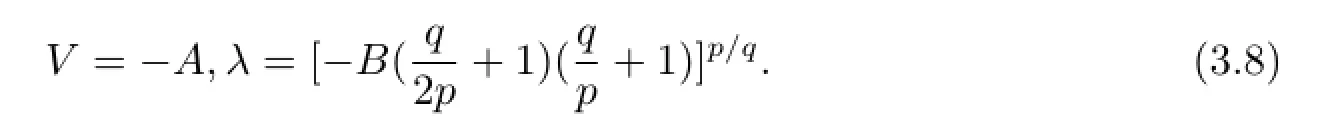
將（2.5）和（3.8）式代入（3.3）式可得到廣義KdV方程的如下形式的解

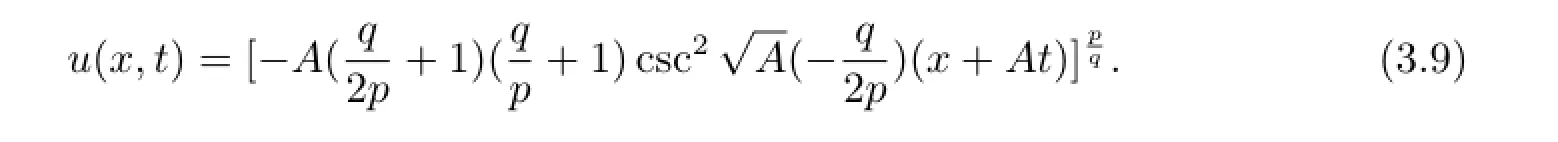
情況3當(dāng)B=-1時，方程（1.8）可變?yōu)榉匠蹋?.6），此時廣義KdV方程有如下形式的解［9］

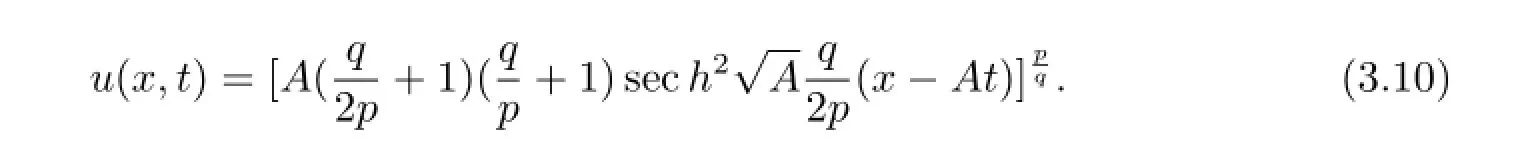
例2廣義ZK方程的解

把u（x，y，t）=u（ξ），ξ=k1x+k2y-V t=1（其中V是待定的常數(shù)）代入方程（1.2）后得

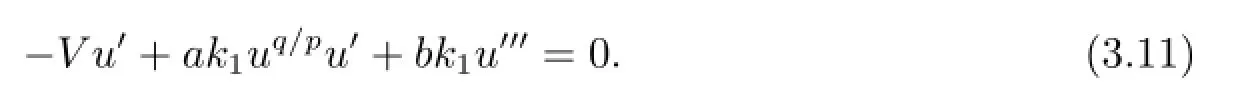
假設(shè)方程（1.2）的形式解為

情況1用常微分方程（1.8）構(gòu)造新解.

將（3.12）式和常微分方程（1.8）一起代入方程（3.11）得

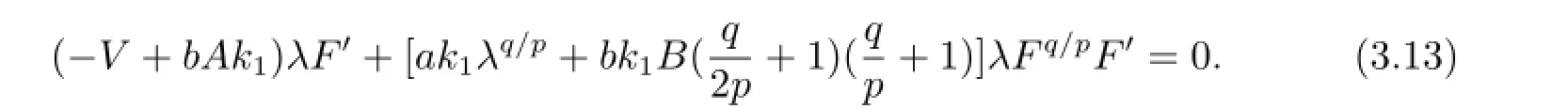
令λF＇，λFq/pF＇的系數(shù)為零可得到

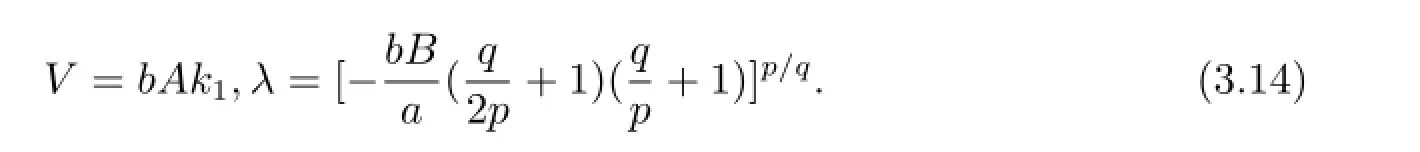
將（2.3）和（3.14）式代入（3.12）式可得到廣義ZK方程的如下形式的解

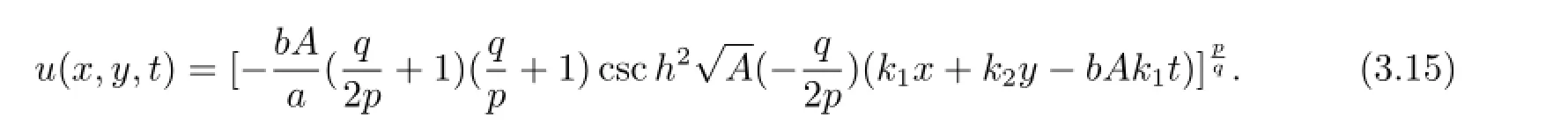
情況2用常微分方程（1.10）來構(gòu)造新解.

將（3.12）式和常微分方程（1.10）一起代入方程（3.11）得

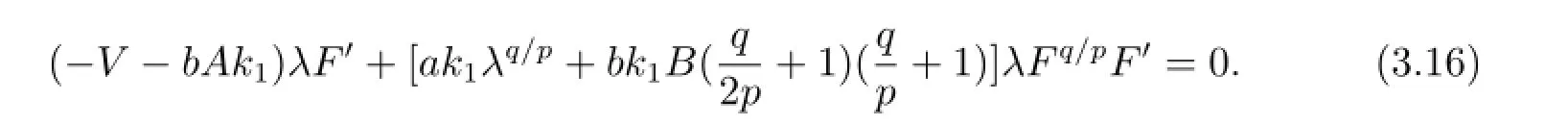
令λF＇，λFq/pF＇的系數(shù)為零可得到

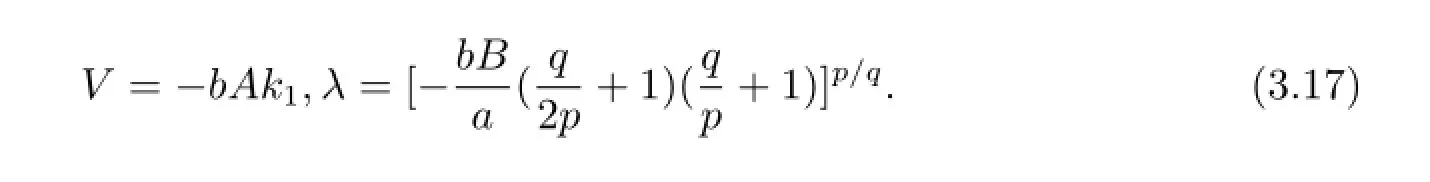
將（2.5）和（3.17）式代入（3.12）式可得廣義ZK方程的如下形式的解

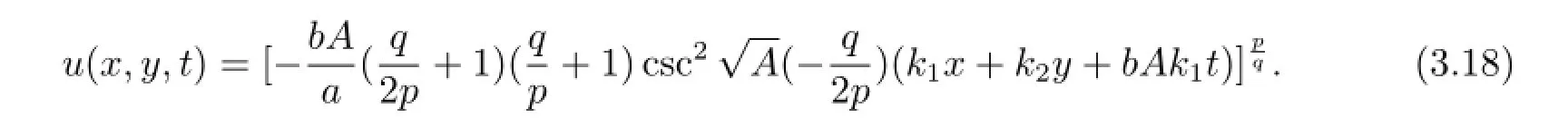
情況3當(dāng)B=-1時，式（1.8）可變?yōu)槭剑?.6），此時廣義ZK方程有如下形式的解［9］

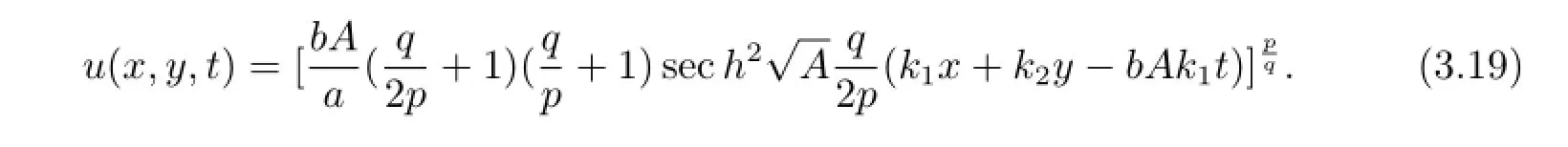
例3廣義Burgers方程的解

把u（x，t）=u（ξ），ξ=x-V t（其中V是待定的常數(shù)）代入方程（1.3）后得

考慮m×q/p+m+q/p=m+q/p×2可得m=1.

假設(shè)方程（1.3）的形式解為

用常微分方程（1.9）（取“+”號形式）來構(gòu)造新解.將（3.21）式和常微分方程（1.9）一起代入方程（3.20）得

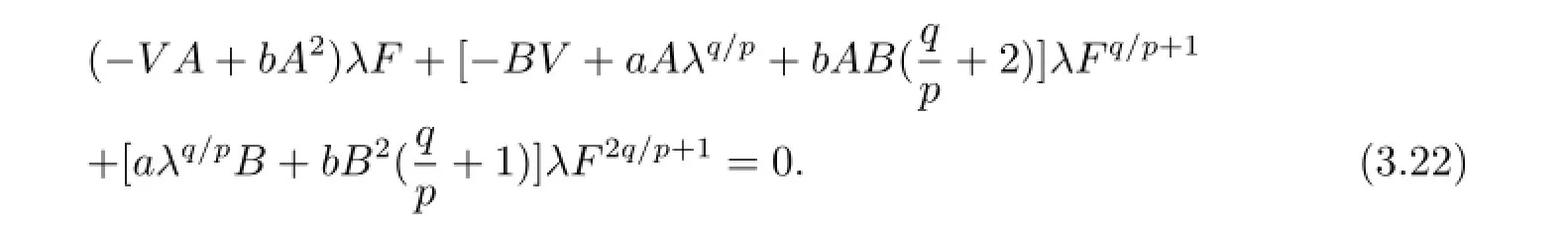
令λF，λFq/p+1，λF2q/p+1的系數(shù)為零可得到

將式（3.23）和（2.4）式（取“-”號形式）代入（3.21）式可得廣義Burgers方程的如下形式的解

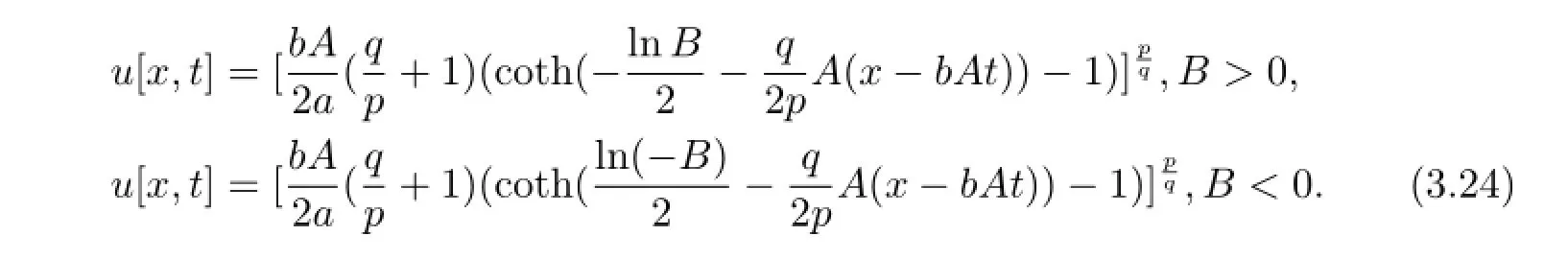
當(dāng)B=-1時，方程（1.9）可變?yōu)榉匠蹋?.7），此時廣義Burgers方程有如下形式的解［9］

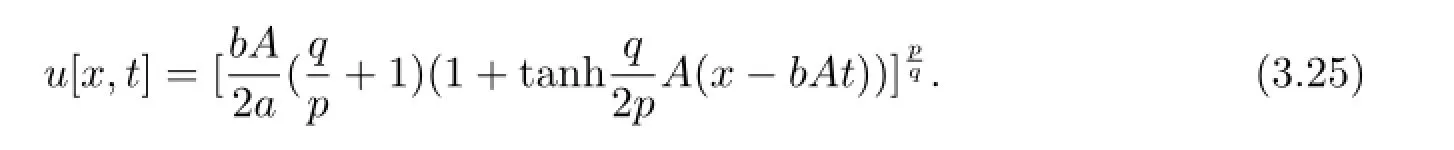
例4廣義KP-Burgers方程的解

把u（x，y，t）=u（ξ），ξ=x+ky-V t（其中V是待定的常數(shù)）代入方程（1.4）后得

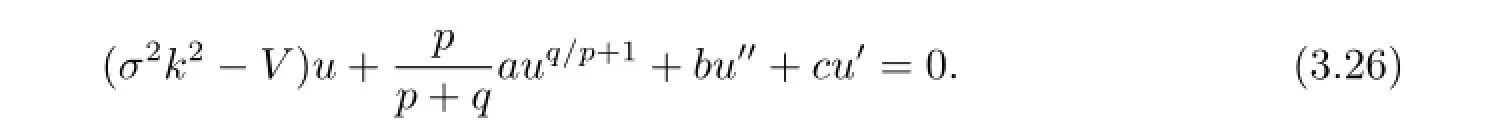
考慮uq/p+1項(xiàng)的次數(shù)和u＇＇項(xiàng)的次數(shù)相等可得m=2.

假設(shè)方程（1.4）的形式解為

用常微分方程（1.9）（取“+”號）來構(gòu)造新解.將（3.27）式和常微分方程（1.9）一起代入方程（3.26）后得

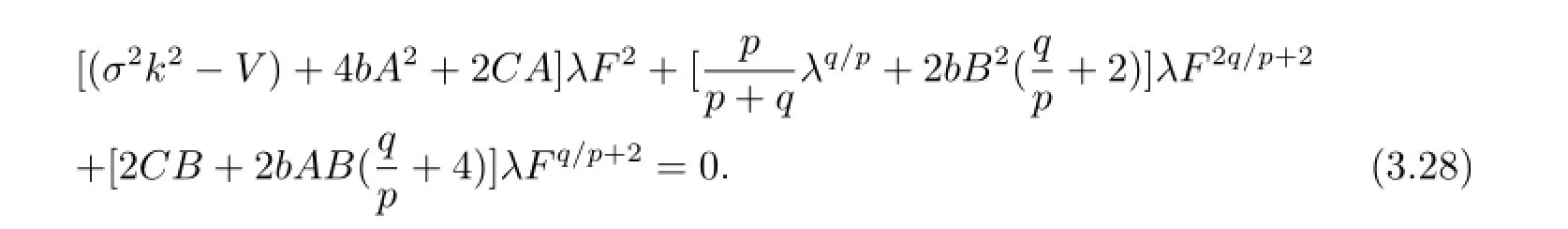
令λF2，λFq/p+2，λF2q/p+2的系數(shù)為零可得到

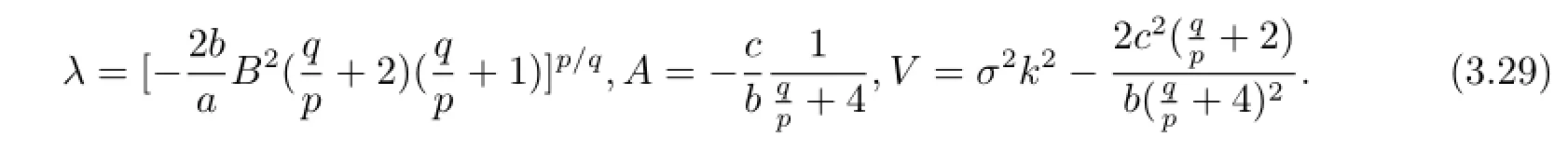
將（3.29）和（2.4）式（取“-”號）代入（3.27）式可得廣義KP-Burgers方程的如下形式的解

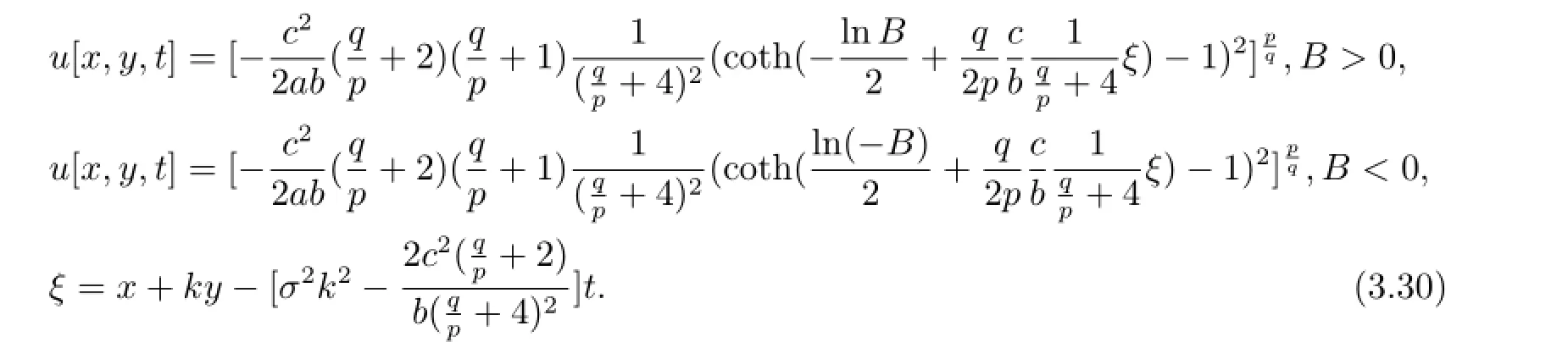
當(dāng)B=-1時，式（1.9）可變?yōu)槭剑?.7），此時廣義KP-Burgers方程有如下形式的解［9］

例5廣義ZK-Burgers方程的解

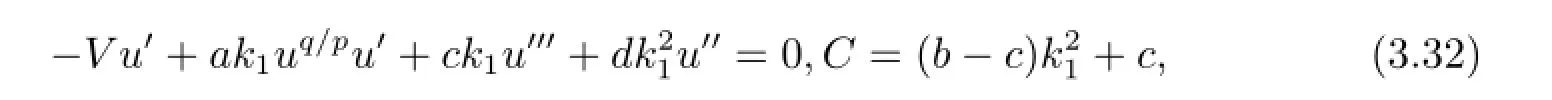
積分得

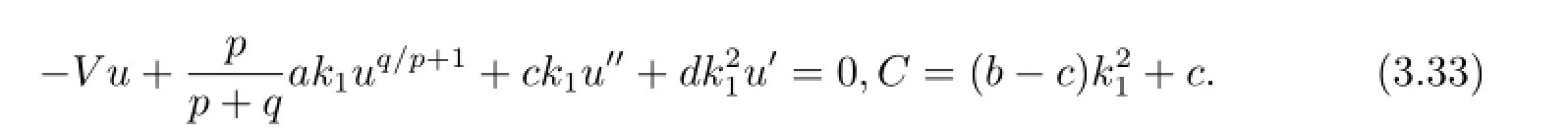
假設(shè)方程（1.5）的形式解為

用常微分方程（1.9）（取“+”號）來構(gòu)造新解.將（3.34）式和常微分方程（1.9）一起代入方程（3.33）后得

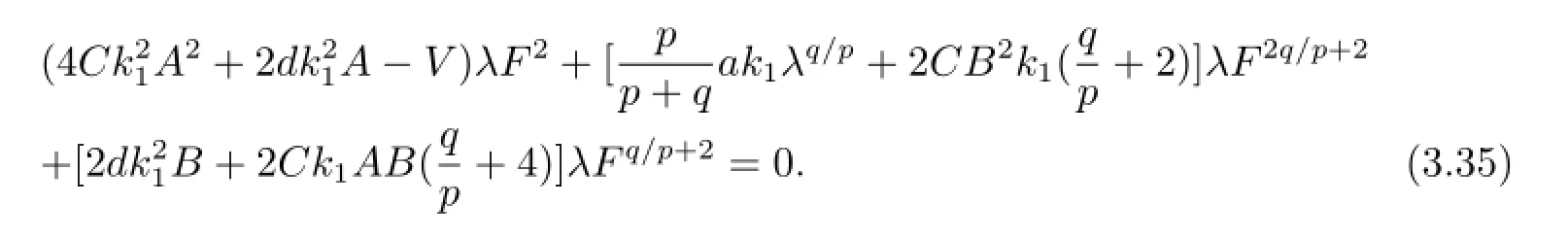
令λF2，λFq/p+2，λF2q/p+2的系數(shù)為零可得到

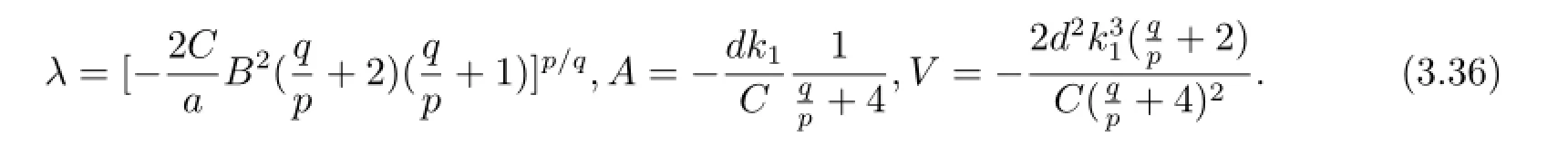
將式（3.36）和（2.4）式（取“-”號）代入（3.34）式可得廣義ZK-Burgers方程的如下形式的解

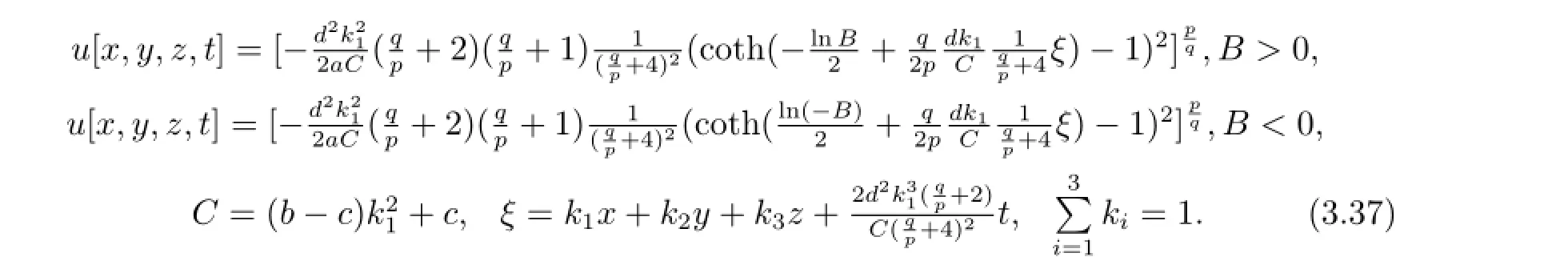
當(dāng)B=-1時，式（1.9）可變?yōu)槭剑?.7），此時廣義ZK-Burgers方程有如下形式的解［9］

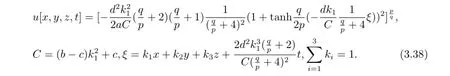
4　結(jié)論

文獻(xiàn)［9］利用輔助方程（1.6）和（1.7）得到了幾種廣義非線性發(fā)展方程的由sech函數(shù)和tanh函數(shù)組成的新解.本文引進(jìn)了包含輔助方程（1.6）和（1.7）的輔助方程（1.8）-（1.10），得到了幾種廣義非線性發(fā)展方程的由雙曲余割函數(shù)、雙曲正切函數(shù)、雙曲正割函數(shù)、雙曲余切函數(shù)和余割函數(shù)組成的新解.

［1］程雪蘋，李金玉，薛江蓉.耦合KdV方程的約化及求解［J］.物理學(xué)報(bào)，2011，60（11）：110204-1-110204-7.

［2］梁立為，李興東，李玉霞.修正的F展開法和推廣的KdV方程新的孤波解和精確解［J］.物理學(xué)報(bào)，2009，58（4）：2159-2163.

［3］套格圖桑，斯仁道爾吉.BBM方程和修正的BBM方程新的精確孤立波解［J］.物理學(xué)報(bào)，2004，53（12）：4052-4060.

［4］套格圖桑，白玉梅.非線性發(fā)展方程的Riemann theta函數(shù)等幾種新解［J］.物理學(xué)報(bào)，2013，62（10）：100201-1-100201-9.

［5］套格圖桑，斯仁道爾吉.mBBM方程和KdV方程新的Jacobi橢圓函數(shù)周期解［J］.內(nèi)蒙古師范大學(xué)學(xué)報(bào)（自然科學(xué)版），2006，35（3）：278-281.

［6］套格圖桑，斯仁道爾吉.KdV方程和KP方程的新的精確孤立波解［J］.內(nèi)蒙古師范大學(xué)學(xué)報(bào)（自然科學(xué)版），2005，34（2）：145-150.

［7］Sun Y Z，Wang Z L，Wang G W，Liu X Q.Soliton solutions for generalized fifth-order KdV and BBM equations with variable coefficients［J］.Chinese J.Quantum Electronics，2013，30（4）：388-404. ［8］Cheng X P，Yang Y Q，Li J Y.Solitary and periodic waves in coupled KdV equations with different linear dispersion relations［J］.Commun.Theor.Phy.，2014，61（1）：1-6.

［9］Wang M L，Li L X，Li E Q.Exact solitary wave solutions of nonlinear evolution equations with a positive fractional power term［J］.Commun.Theor.Phy.，2014，61（1）：7-14.

THE NEW SOLUTIONS OF SOME KINDS OF GENERALIZED NONLINEAR EVOLUTION EQUATIONS

LI Ning，Taogetusang
（School of Mathematical Sciences，Inner Mongol Normal University，Hohhot 010022，China）

In this paper，we study the problem of constructing the new solutions of the generalized KdV equation，the generalized KP-Burgers equation and some other kinds of generalized nonlinear evolution equations.By using three kinds of auxiliary equations and their new solutions，the new solutions of generalized KdV equation，generalized KP-Burgers equation and some other kinds of generalized nonlinear evolution equations are constructed.These solutions are consisting of hyperbolic cosecant function，hyperbolic tangent function，hyperbolic secant function，hyperbolic cotangent function and cosecant function.

auxiliary equation；generalized KdV equation；generalized KP-Burgers equation

MR（2010）主題分類號：35Q51O175.29

A

0255-7797（2016）05-1103-08

2014-05-12接收日期：2014-09-03

國家自然科學(xué)基金資助（11361040）；內(nèi)蒙古自治區(qū)高等學(xué)校科學(xué)研究基金資助（NJZY12031）；內(nèi)蒙古自治區(qū)自然科學(xué)基金資助（2015MS0128）.

李寧（1989-），男，河北石家莊，碩士，主要研究方向：孤立子與可積系統(tǒng)理論及其應(yīng)用.

2010 MR Subject Classification：35Q51