與分擔函數相關的正規定則

楊端陽，葉亞盛

（上海理工大學理學院，上海200093）

與分擔函數相關的正規定則

楊端陽，葉亞盛

（上海理工大學理學院，上海200093）

本文研究了與分擔函數相關的亞純函數族的正規性的問題.利用Nevanlinna理論的方法，得到了一個正規定則，推廣了龐學誠和Zalcman［3］的一個結果.

正規族；分擔值；分擔函數；亞純函數

1　引言

設區域D為復平面C上的一個區域，F是區域D內的亞純函數族.若對于F中任一函數序列均可選出一個子序列在區域D上按球距內閉一致收斂，則稱F在區域D內正規.設f（z）和g（z）是區域D內的兩個亞純函數，a和b是兩個復數，若當f（z）=a，有g（z）=b，記f（z）=a?g（z）=b.若f（z）=a?g（z）=b和g（z）=b?f（z）=a，記f（z）=a?g（z）=b.若f（z）=a?g（z）=a.則稱f（z）和g（z）是區域D上IM分擔a.

1979年，顧永興證明了Hayman關于正規族的猜想，得到如下著名的正規定則.

定理A［1］設F是區域D內的亞純函數族，k是一個正整數.若對于F中的每一個函數f，有f（z）/=0，f（k）（z）/=1.則F在區域D內正規.

1986年，楊樂改進了定理A的結果，得到

定理B［2］設F是區域D內的亞純函數族，k是一個正整數，h（z）（/≡0）是區域D內的全純函數.若對于任意的f∈F，f（z）/=0，f（k）（z）/=h（z），則F在區域D內正規.

2002年，龐學誠和Zalcman考慮涉及零點重級的亞純函數的情況，證明了

定理C［3］設k是一個正整數，h（z）（/≡0）是區域D內的全純函數，F是區域D內的亞純函數族，其零點重級均至少為k+3.若對于任意的f∈F，f（k）（z）/=h（z），則F在區域D內正規.

推廣定理C，得到如下結果

定理1設k是一個正整數，M是正數，h（z）（/≡0）是區域D內的全純函數，F是區域D內的亞純函數族，其零點重級均至少為k+3.若對于任意f∈F，f（k）（z）h（z）?|f（z）|≥M，則F在區域D內正規.

例1設D=z：|z|≤1，h（z）=z，F=｛fn（z）｝，其中.當時，|fn（z）|=0.然而F在區域D內不正規，這是因為當n→∞時，→∞，fn（0）=0.

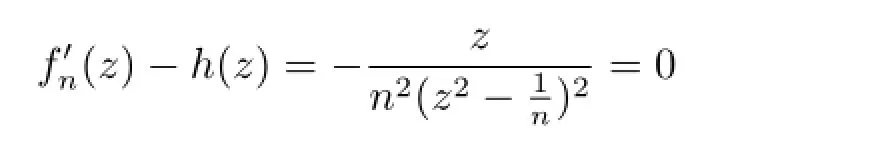
例1說明f（k）（zh（z）?|f（z）|≥M是個必要條件.

在文獻［3］中的例1說明零點重級均至少為k+3也是必要的.

定理2設k是一個正整數，h（z）（/≡0，∞）是區域D內的亞純函數，其極點的重級均之多為k-1，F是區域D內的亞純函數族，其零點重級均至少為k+3.若對于任意的f∈F， f（k）（z）h（z）?|f（z）|≥M，則F在區域D內正規.

2　相關引理

為了證明定理，需要下面的引理

引理2.1［4］設k是一個正整數，F是單位圓盤上的亞純函數族，其零點重級至少為k，且存在A≥1，使得對于任意f，在f零點處，都有|f（k）（z）|≤A.假設F在z0處不正規，則對0≤α≤k任意，必存在

a.點列zn，zn→z0；

b.函數列fn∈F；

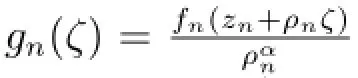
引理2.2［5］設k是一個正整數，f（z）是超越亞純函數，R（z）（/≡0）是有理函數.若除有限個點外，f（z）的零點重級至少為k+2，那么f（k）（z）-R（z）有無窮多個零點.

引理2.3［6］設k是一個正整數，f（z）是有窮級亞純函數，其零點重級均至少為k+2.若f（k）（z）/=1，則f（z）是常數.

引理2.4［3］設f（z）是非常數有理函數，k，m是正整數.若f（z）的零點重級均至少為k+3，則對于任意正整數m，在復平面上f（k）（z）=zm有解.

引理2.5［7］設F是單位圓盤上的亞純函數族，a是一個有窮復數或∞，且每個任意f∈F，f/=a.若F在△＇內正規，在z=0處不正規，則存在F的子列fn，使得fn→a在△＇內.

引理2.6［8］設k，m是一個正整數，f（z）是有理函數，其零點的重級均至少為k.如果f（k）（z）/=z-m，那么f（z）是常數.

引理2.7設｛fn（z）｝是區域D內的亞純函數列，其零點重級均至少為k+3，｛hn（z）｝是區域D內的全純函數列，并且一致收斂于全純函數h（z）（/=0）.若對于任意正整數n，=hn（z）?|hn（z）|≥M，則｛fn（z）｝在區域D內正規.

證設z0為D內任意一點，下證｛fn（z）｝在z0處正規.由于h（z）/=0，不妨設h（z0）=1.假設｛fn（z）｝在z0處不正規，由引理2.1，存在點列zn，zn→z0，｛fn（z）｝的子列（仍記為｛fn（z）｝），正數列ρn→0，使得在復平面C上按球距內閉一致收斂于非常數亞純函數g（ζ），其零點重級至少為k+3，級至多為2.

斷言：g（k）（ζ）/=1.

若不然，存在ζ0，使得g（k）（ζ0）=1.顯然g（k）/≡1.否則，g（ζ）是次數為k的多項式，這與g（ζ）的零點重級至少為k+3矛盾.又因為（zn+ρnζ）-hn（zn+ρnζ）=-hn（zn+ρnζ）→g（k）（ζ）-1，由Hurwitz定理，存在ζn，ζn→ζ0，使得當n充分大時，（zn+ρnζn）=hn（zn+ρnζn），根據條件可得|fn（zn+ρnζn）|≥M，則

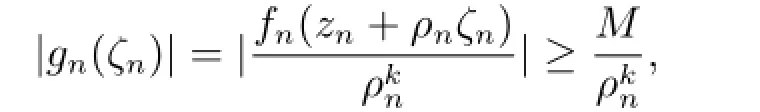
由于g（ζ）的零點重級至少為k+3，由引理2.3，g（ζ）是常數，矛盾.

3　定理的證明

定理1的證明不妨設D為△，z0為△內任意一點.下證F在z0處正規.下面分兩種情況討論.

情形1 h（z0）/=0，則存在δ＞0，使得在△（z0，δ）內，h（z）/=0.由引理2.7，F在z0處正規.

情形2 h（z0）=0.不失一般性，令z0=0，h（z）=zmφ（z），其中在△內φ（0）=1，φ（z）/= 0.由情形1，F在△＇=△｛0｝內正規，下證F在z0=0處正規.

令F∞：｛F（z）=，f∈F｝.顯然f（0）/=0.否則，f（0）=0.由于f零點重級均至少為k+3，則f（k）（0）=0，即f（k）（0）=h（0），根據條件0=|f（0）|≥M，矛盾.由于f（0）/=0，則F（0）=∞.下證F∞在z0=0處正規.

假設F∞在z0=0處不正規，由引理2.1，存在點列zn，zn→0，函數列Fn∈F∞，正數列ρn→0+，使得

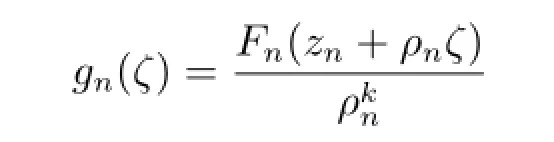
在復平面C上按球距內閉一致收斂于非常數亞純函數g（ζ），其零點重級至少為k+3，級至多為2.

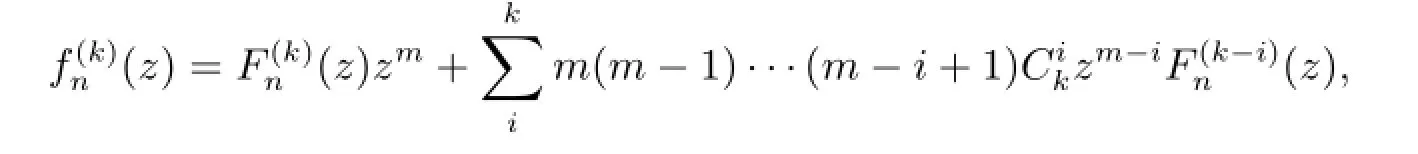
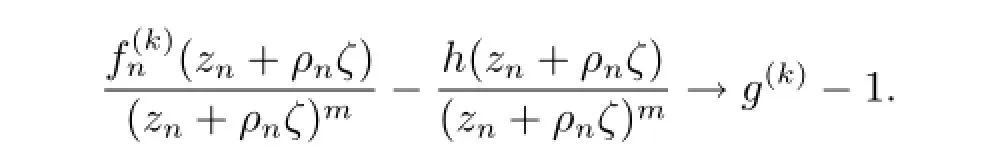
斷言：g（k）（ζ）/=1.

若不然，存在ζ0，使得g（k）（ζ0）=1.顯然，g（k）（ζ）/=1.否則，g（ζ）是次數為k的多項式，這與g（ζ）的零點重級至少為k+3矛盾.由Hurwitz定理，存在ζn，ζn→ζ0，使得當n充分大時，（zn+ρnζn）=h（zn+ρnζn）.根據條件可得|fn（zn+ρnζ）|≥M，則

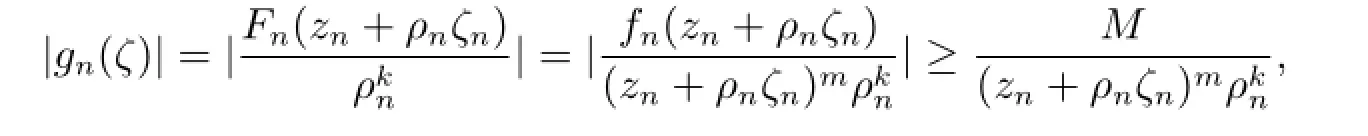
由于g（ζ）的零點重級至少為k+3，由引理2.3，g（ζ）是常數，矛盾.

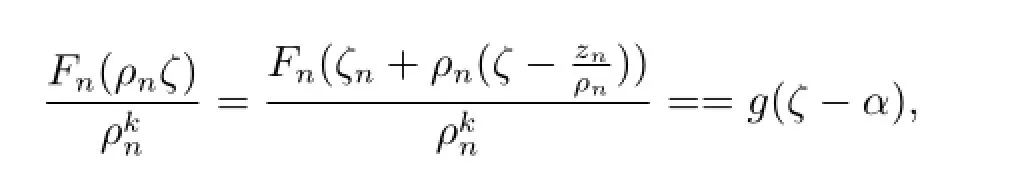
所以g（ζ-α）的零點重級至少為k+3，并且0是g（ζ-α）的重級至少為m的極點.

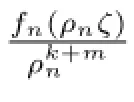
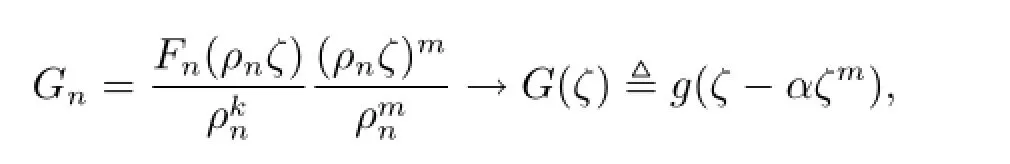
其中G（ζ）的零點重級至少為k+3.由于0是g（ζ-α）的重級至少為m的極點，所以G（0）/=0.

斷言：G（k）（ζ）/=ζm.

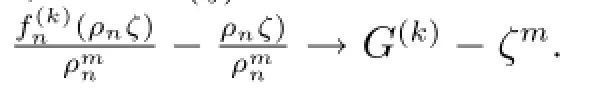
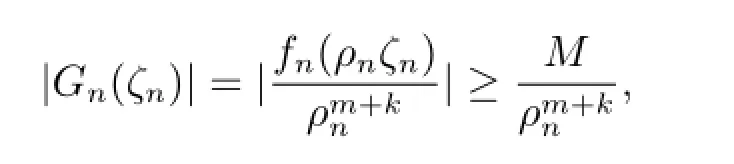
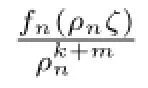
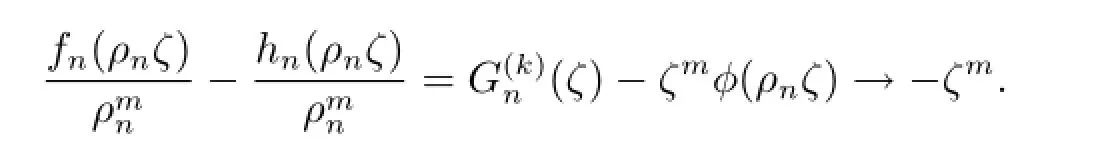
首先假設fn（z）在△δ∈△內上全純函數.因為fn（z）在內正規，但是在0處不正規，由最大模型原理fn（z）→∞于內.

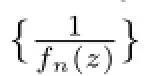
令

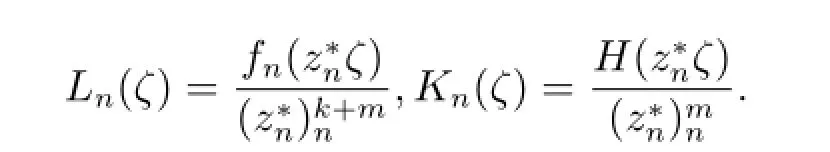
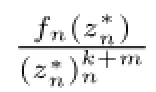
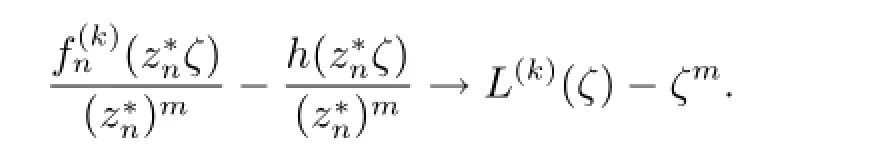
由Hurwitz定理，存在ζn，ζn→ζ0，使得當n分大時，，根據條件可得≥M，則

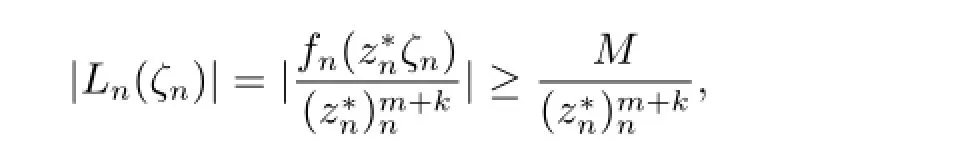
令

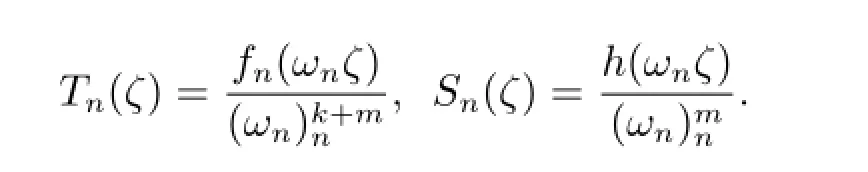
于是Tn（ζ）為復平面上的亞純函數列，其零點的重級至少為k+3，Sn（ζ）為全純函數列且一致收斂于ζm.根據條件可得（ζ）=Sn（ζ）?|Tn（ζ）|≥M，由引理2.7，Tn（ζ）在C｛0｝內正規.顯然

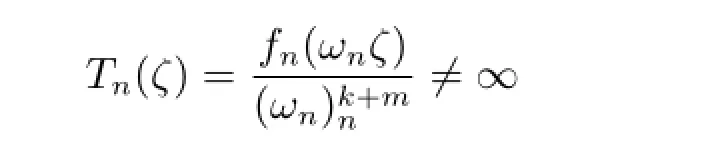
在△內.否則，存在ηn，使得Tn（ηn）=∞，則fn（ωnηn）=∞.顯然|ωnηn|=|ωn||ηn|＜|ωn|，這與ωn是fn模最小的極點矛盾.再根據最大模原理以及Montel定則，故Tn（ζ）在C內正規.

設Tn（ζ）→T（ζ），其中T（ζ）的零點重級至少為k+3.顯然，T（k）（ζ）-ζm有零點.否則，T（k）（ζ）/=ζm，從而T（k）（0）/=0m.又因為Tn（0）=Gn（0）→0，而且T（ζ）的零點重級至少為k+3，則T（k）（0）=0，矛盾.顯然，T（k）（ζ）≡ζm.否則，T（k）（1）≡1m.又由于

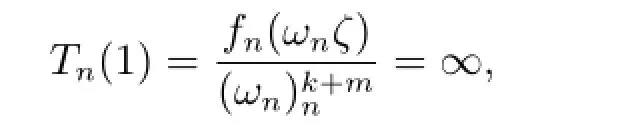
矛盾.于是設ζ0是T（k）（ζ）-ζm的零點，又因為

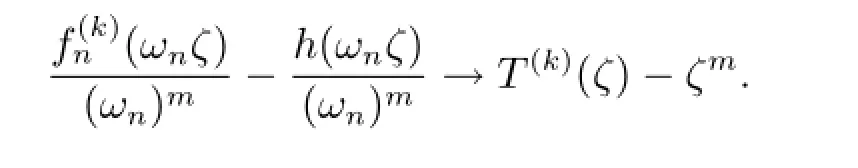
由Hurwitz定理，存在ζn，ζn→ζ0，使得當n分大時，（ωnζn）-h（ωnζn），根據條件可得|fn（ωnζn）|≥M，則

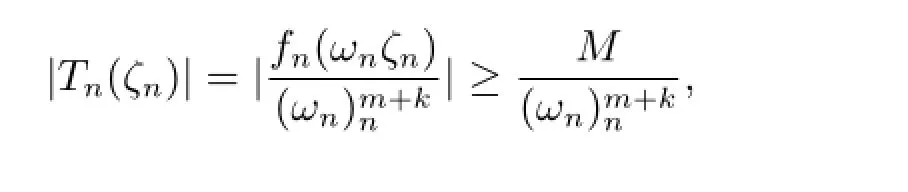
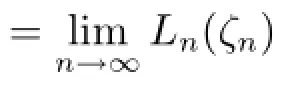
由于F∞在z0處正規，由條件知對于任意Fn∈F∞，有Fn（0）=∞，存在δ＞0，使得|F（z）|≥1在△δ內，所以當n充分大時，|Fn（z）|≥.故在△δ1內fn（z）/=0，則在△δ1內是全純函數列，因此

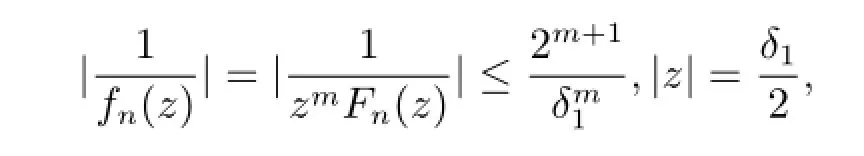
再由最大模原理以及Montel定則知F在z0處正規.故F在區域D內正規.

定理2的證明利用引理2.2和2.6，類似于定理1方法可證得.

［1］Gu Y X.A normal criterion of meromorphic families［J］.Sci.Sinica，Math.，1979，（I）：267-374.

［2］Yang L.Normality of families of meromorphic functions［J］.Scientia.Sinica.，1986，A（9）：898-908.

［3］Pang X C，Yang D G，Zalcman L.Normality families of meromorphic functions whose derivatives omit a function［J］.Comput.Meth.Funct.The.，2002，2：257-265.

［4］Pang X C，Zalcman L.Normal families and shared values［J］.Bull.London.Math.Soc.，2000，32：325-331.

［5］Xu Y.Picard Values and derivatives of meromorphic functions［J］.Kodai.Math.J.，2005，28：99-105.

［6］Wang Y F，Fang M L.Picard values and normal families of meromorphic functions with multiple zeros［J］.Acta Math.Sci.，1998，1：17-26.

［7］楊劉，陳巧玉.與例外函數相關的正規族［J］.華東師范大學學報，2013，2：154-159.

［8］Xu Y.Normal families and exceptional functions［J］.J.Math.Anal.Appl.，2007，329：1343-1354.

［9］李銘，黃斌.亞純函數族的一個正規定則［J］.數學雜志，2014，3（34）：539-545.

［10］徐焱.亞純函數的正規族［J］.數學雜志，2001，4（21）：381-386.

NORMALITY ON SHARING FUNCTIONS

YANG Duan-yang，YE Ya-sheng
（School of Science，University of Shanghai for Science and Technology，Shanghai 200093，China）

In this paper，we study the normality of the family of meromorphic functions about sharing functions.By using Nevanlinna theory method，we obtain a normal criterion，which improves a results got by Pang and Zalcman［3］.

normal family；sharing values；sharing functions；meromorphic function

MR（2010）主題分類號：30D45O174.52

A

0255-7797（2016）05-1091-06

2015-05-02接收日期：2015-06-02

國家自然科學基金項目（11371139）.

楊端陽（1989-），女，河南信陽，碩士，主要研究方向：復分析.

2010 MR Subject Classification：30D45