THE MINIMAL SOLUTION OF A SPECIAL ANTICIPATED BACKWARD STOCHASTIC DIFFERENTIAL EQUATION

TU Shu-heng，LIAO Jun-jun

(1.School of Science，Henan University of Technology，Zhengzhou 450002，China）

(2.School of Mathematics and Statistics，Huazhong University of Science and Technology，Wuhan 430074，China）

THE MINIMAL SOLUTION OF A SPECIAL ANTICIPATED BACKWARD STOCHASTIC DIFFERENTIAL EQUATION

TU Shu-heng1，LIAO Jun-jun2

(1.School of Science，Henan University of Technology，Zhengzhou 450002，China）

(2.School of Mathematics and Statistics，Huazhong University of Science and Technology，Wuhan 430074，China）

In this paper，we study the problem of a minimal solution to a special class of anticipated backward stochastic differential equation.When the generator is continuous and satisfying a similar linear growth condition，we prove the existence of minimal solutions.Here，our hypotheses are weaker than the before papers，however，we obtain a better lemma and the same result.

anticipated backward stochastic differential equations；minimal solution；comparison theorem

2010 MR Subject Classification：60H99；60G99

Document code：AArticle ID：0255-7797（2016）05-0940-09

1 Introduction

The notions of non-linear backward stochastic differential equations（BSDEs）were introduced by Pardoux and Peng［11］.A solution of this equation，associated with a terminal value ξ and a generator or coefficient f（t，ω，y，z），is a couple of adapted stochastic processes （Y（t），Z（t））｛t∈［0，T］｝such that

where W is a d-dimensional standard Brownian motion.This type of nonlinear backward stochastic differential equations were first studied by Pardoux and Peng in［11］，and they established the existenceness and uniqueness of adapted solution under the global Lipschitz condition.Since then，many people try to weaken the conditions of generators to get the same results and study some different forms of BSDEs.For examples，Aman and Nz'i［1］studied BSDEs with oblique reflection and local Lipschitz.Bahlali［2］studied backwardstochastic differential equations with locally Lipschitz coefficients.Situ［9］and Royer［10］studied BSDEs with jumps.It is now well-known that BSDEs provide a useful framework for formulating a lot of mathematical problems such as used in financial mathematics，optimal control，stochastic games and partial differential equations（see［12-14］）.Based on the above applications，specially in the field of finance，and optimal control，recently，a new type of BSDEs，called anticipated BSDEs（ABSDEs），were introduced by Peng and Yang［4］as the following

where θ（·）：［0，T］→R+，?（·）：［0，T］→R+are continuous functions and satisfy that （i）there exists a constant K≥0 such that for each t∈［0，T］，

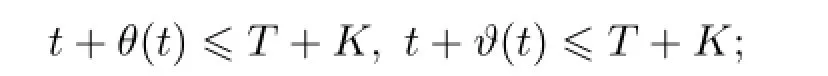
（ii）there exists a constant L≥0 such that for each t∈［0，T］and each nonnegative integrable function g（·），

Under global Lipschitz conditions，Peng and Yang proved the existencenee and uniqueness of solution（see Theorem 4.2 in［4］）.

For anticipated BSDEs，we mention that the generator includes not only the values of solutions of presents but also the future.So ABSDEs may be used in finance.From Theorem 2.1 in［4］，we know that there is a duality between stochastic differential equations with delay and anticipated BSDEs which can be used in optimal control.We also mention that，following Peng and Pardoux［11］，many papers were devoted to BSDEs with continuous coefficients.Especially，many scholars studied the minimal solution of BSDEs，it is refered to［3，5-8］.

Motivated by the above papers，in this paper，we study a special class of 1-dimension ABSDEs as the following

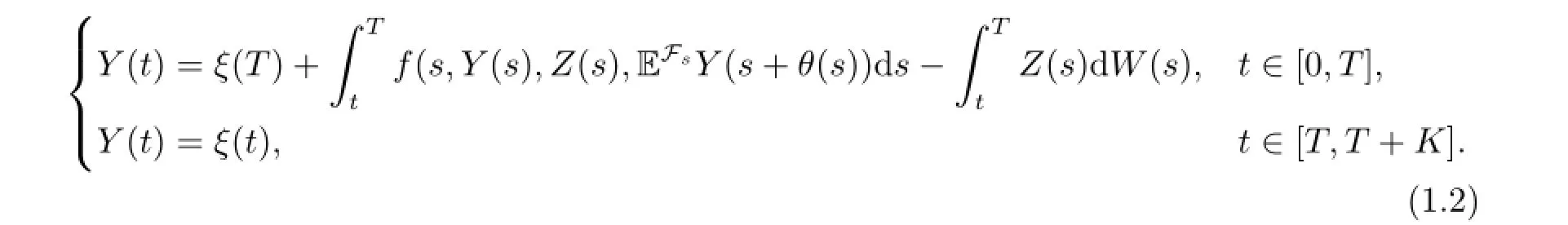
2 Main Reaults

Before starting our main results，we give some necessary notions and hypotheses.

2.1 Preliminaries

Let（?，F(xiàn)，P）be a complete probability space，and let（W（t））t∈［0，T］be a d-dimensional standard Brownian motion on（?，F(xiàn)，P）.Let｛Ft｝t∈［0，T］be the natural filtration generated by W.

·L2（FT；R）｛R-valued FT-measurable random variables such that E［|ξ|2］＜∞｝；

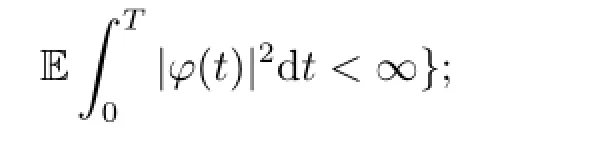
We also need the following assumptions.

（H1）Assume that for all t∈［0，T］，g（t，ω，y，z，μ）：［0，T］×?×R×Rd×L2（Fr；R）→L2（Ft；R），where r∈［t，T+K］，and g satisfies the following conditions

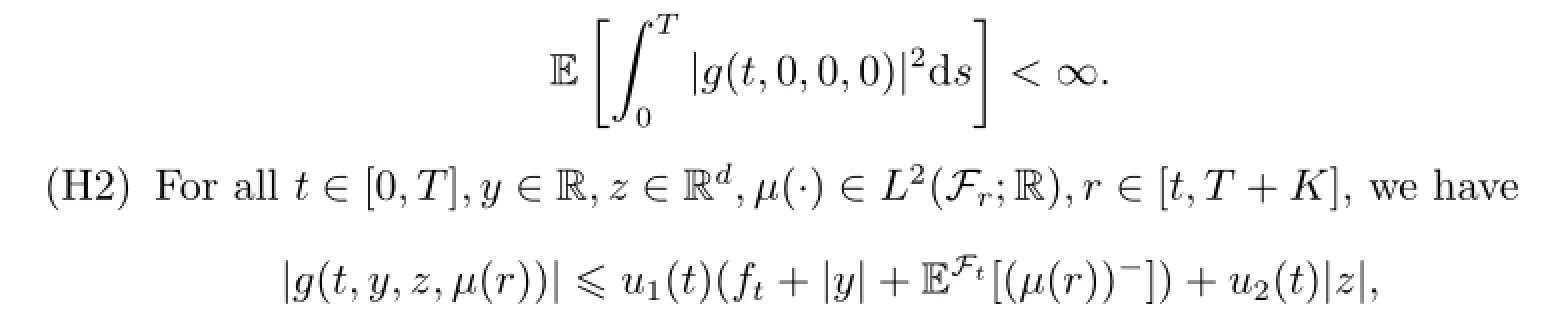
moreover，u1（t）≤u1（t+θ（t）），θ（t）satisfies（i）and（ii）.

Lemma 2.1 Set

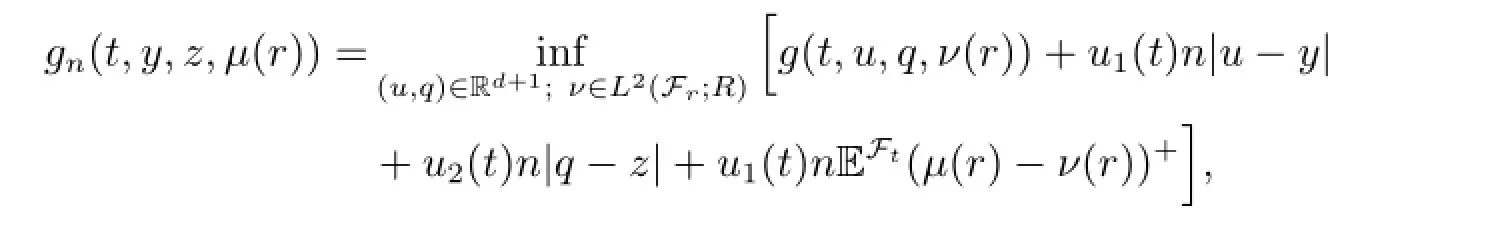
then gn（t，y，z，μ（r））has the following properties.

（a）Linear growth：for any t∈［0，T］，y∈R，z∈Rd，μ（·）∈L2（Fr；R），r∈［t，T+K］，we have

（b）Monotone property in n：for any t∈［0，T］，y∈R，z∈Rd，μ（·）∈L2（Fr；R），r∈［t，T+K］，gn（t，y，z，μ（r））≤gn+1（t，y，z，μ（r））≤g（t，y，z，μ（r）），and gn（t，y，z，·）is increasing.

（c）Lipschitz condition：for any t∈［0，T］，y，y＇∈R，z，z＇∈Rd，μ（·），μ＇（·）∈L2（Fr；R），r∈［t，T+K］，|gn（t，y，z，μ（r））-gn（t，y＇，z＇，μ＇（r））|≤u1（t）|y-y＇|+u2（t）|z-z＇|+u1（t）EFt|μ（r）-μ＇（r）|.

Proof We use the similar method as used in［3，6］to prove（a），（b）and（c）are obvious. We only need to prove（d）.By the definition of infimum，for each n∈N，n＞1，there exist un∈R，qn∈Rd，νn∈L2（Ft；R），r∈［t，T+K］，such that

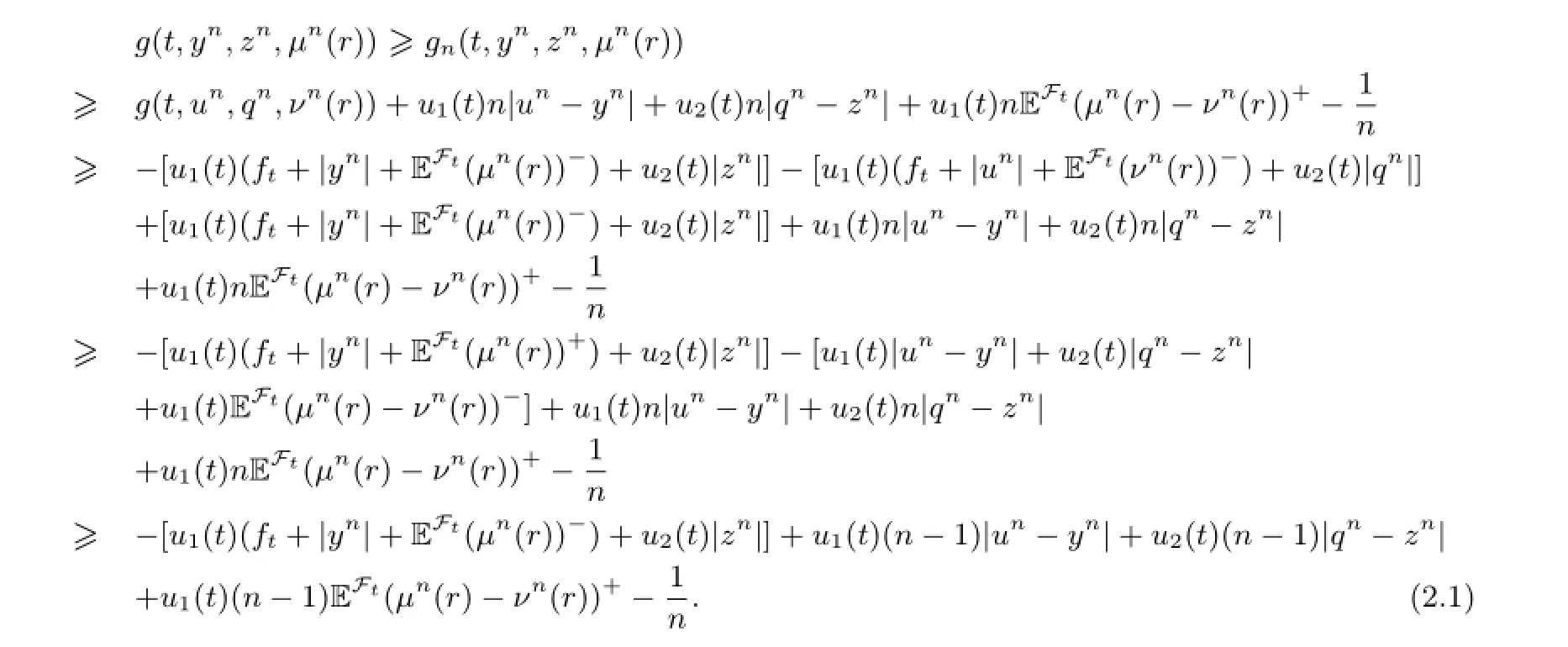
For the above proof，we apply the triangle inequality a±-b±≤（a-b）±and a-=（-a）+. Thus we have

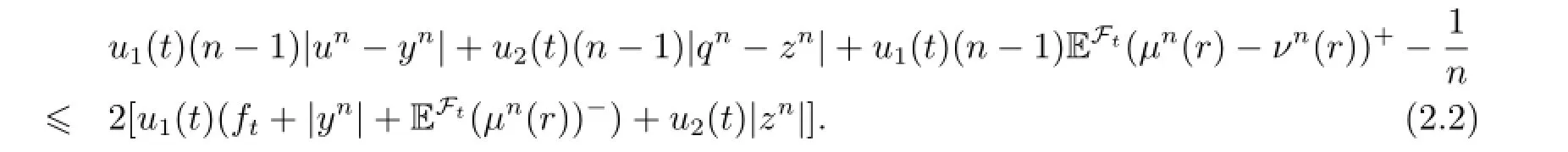
Since E［|EFt（μn（r））-|2］≤E［EFt|（μn（r））|2］≤E|μn（r）|2＜∞，then when n∈N，n＞1，we derive

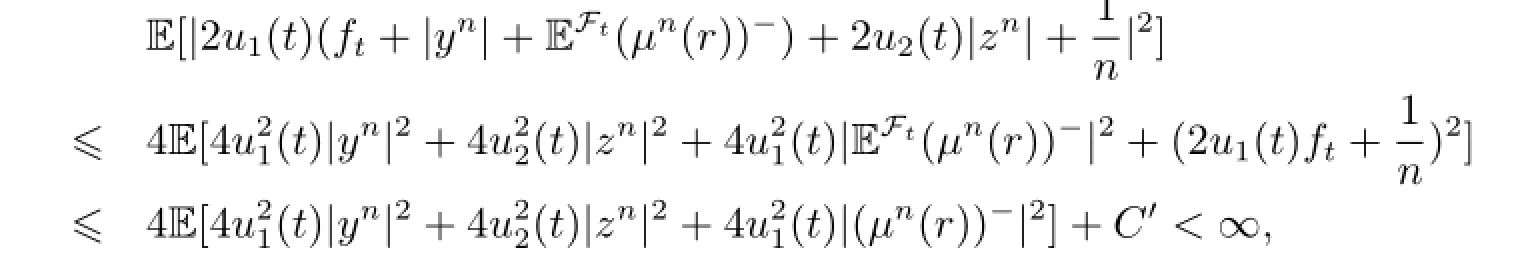
therefore

For an appropriate A＞0，there exists a N＞0，such that for any n＞N，

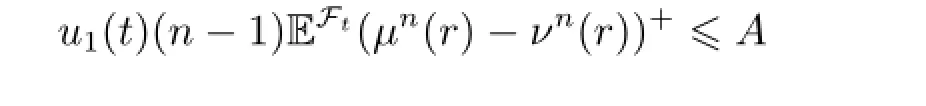
and

Then

By the above inequality，we know｛EFt（μn（r）-νn（r））+；n∈N，n＞1｝is bounded in L2（Ft；R），with（2.4），we get

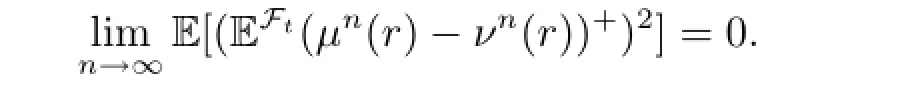
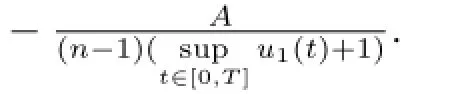
Since g is continuous in L2（F；R），we have

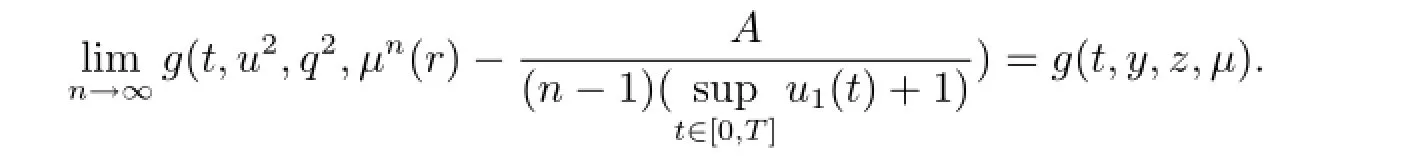
From assumption（H3），we obtain（t，yn，zn，μn（r））=g（t，y，z，μ（r））.

Consider the following equations

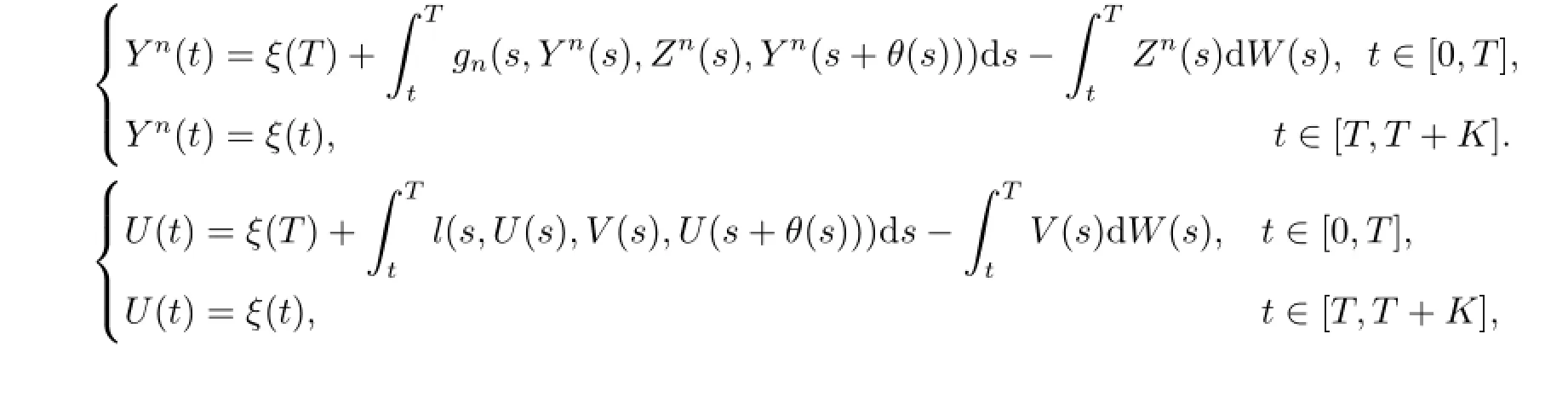
where l（t，y，z，μ（r））=C（ft+|y|+|z|+EFt（μ（r））-），by the comparison theorem in［4］，for any t∈［0，T+K］，n≥m，m，n∈N，U（t）≥Yn（t）≥Ym（t）a.e..

Before giving our main result，we give the following lemma.

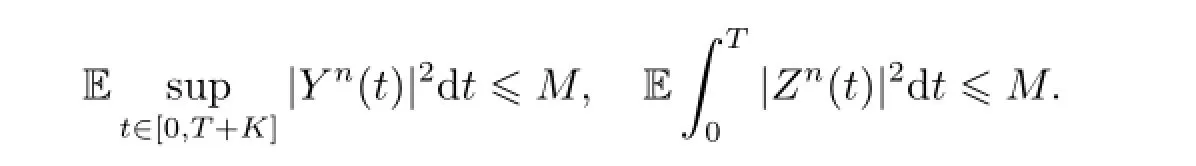
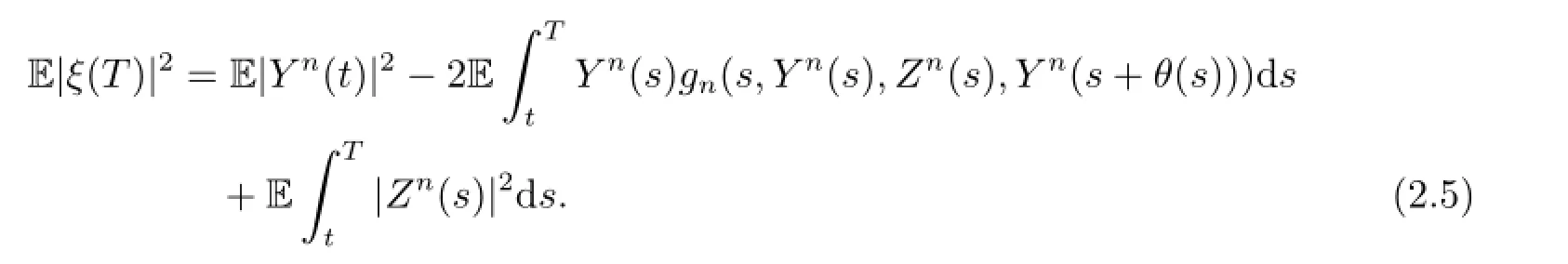
Thus by（H1）-（H3），（i），（ii）in introduction and Lemma 2.1（b），Young's inequality，F(xiàn)ubini's lemma，（a+b+c）2≤C（a2+b2+c2），H¨older's inequality，we have

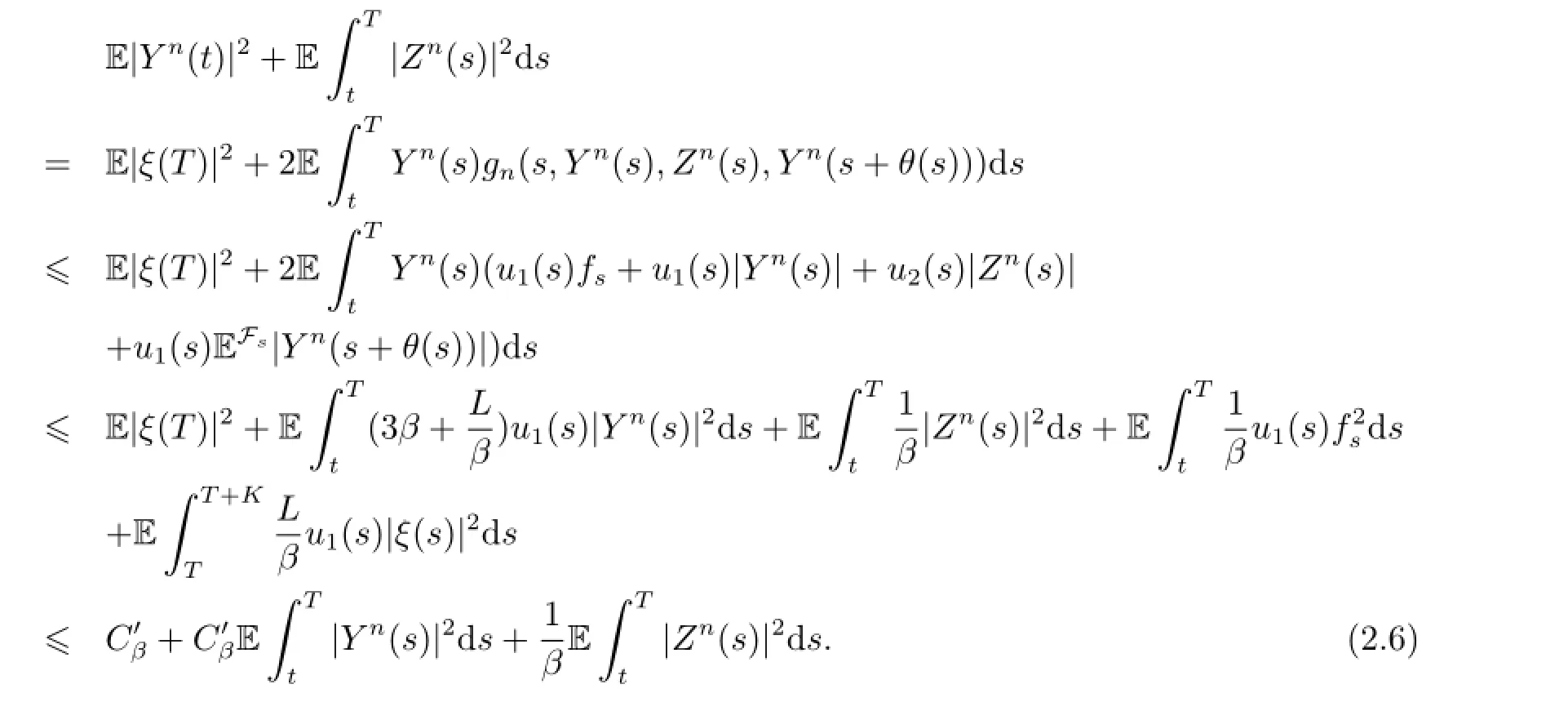
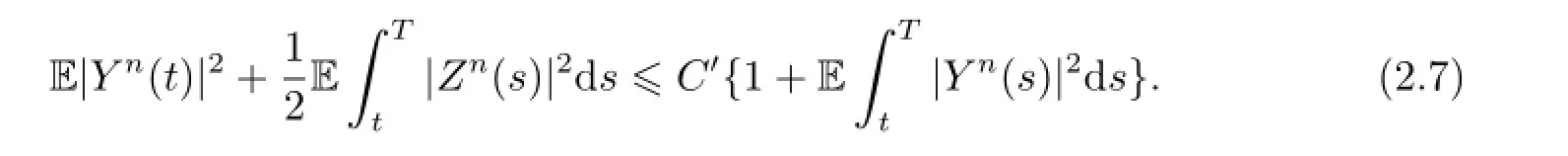
By Gronwall's lemma，we obtain

Thus

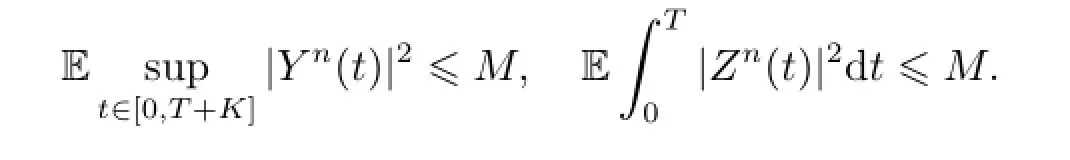
Theorem 2.3（Minimal-solution theorem）Under assumptions（H1）-（H3），（i），（ii），equation（1.2）has a minimal solution，that is ifY＇is another solution of equation（1.2）. Then for any given terminal value ξ（·）∈（T，T+K；R），we have

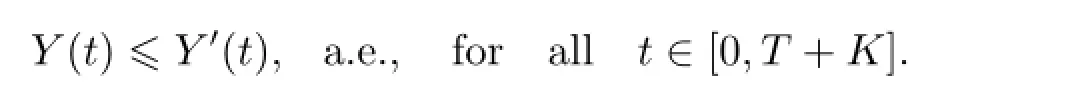
By Lemma 2.1，Lemma 2.2，we have

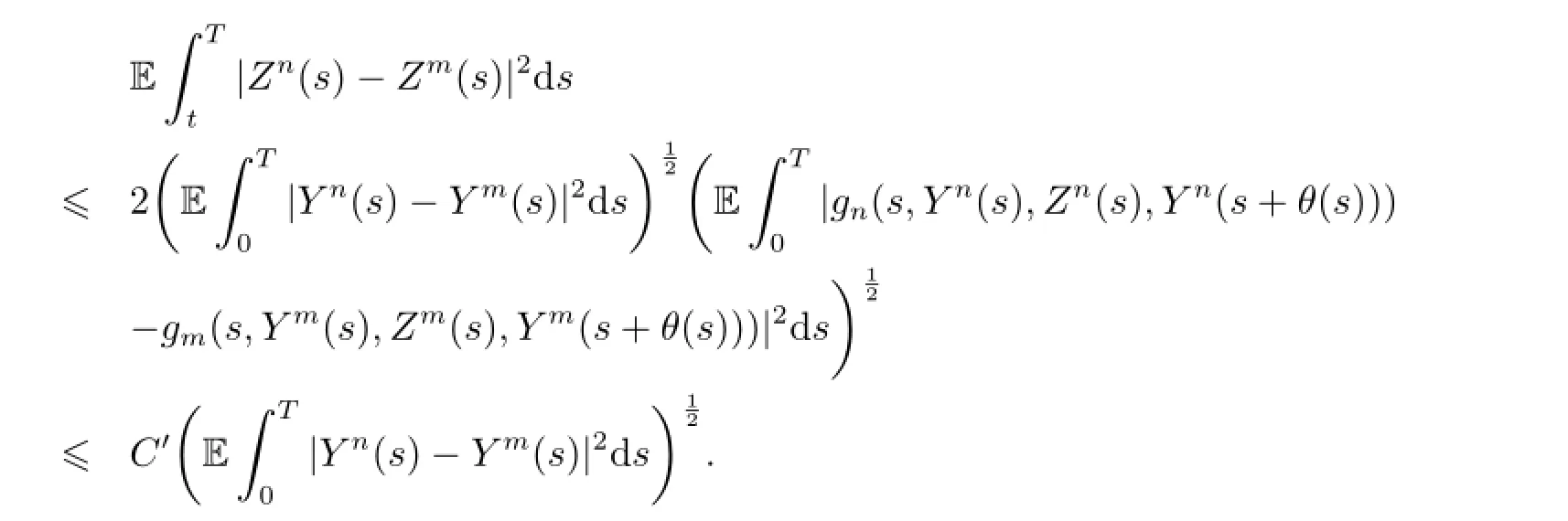
Thus

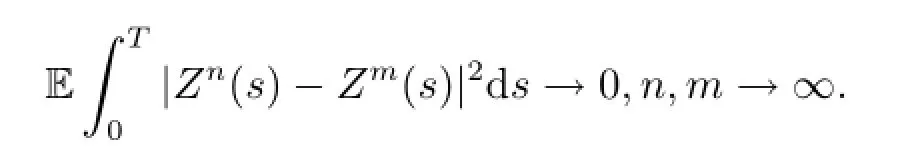
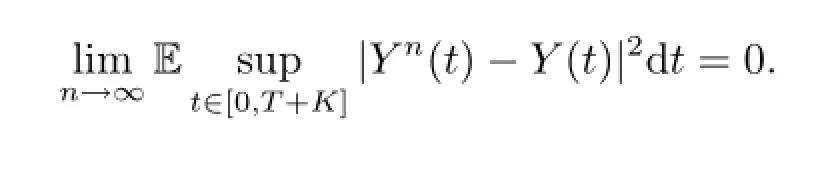
Furthermore，there exists a subsequence of｛n｝，which we still denote this subsequence by ｛n｝such that

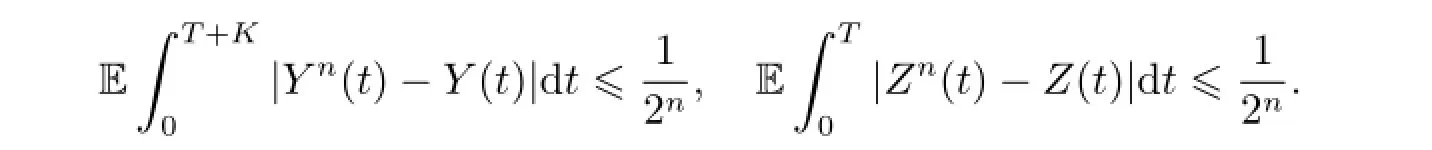
By the linear growth，we get

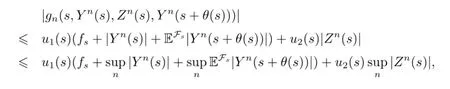
while

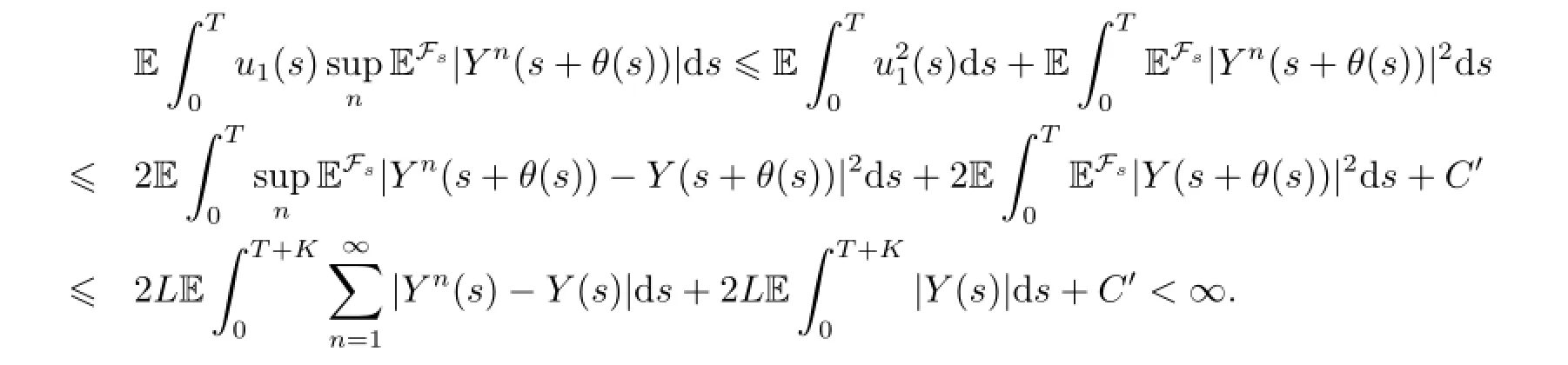
Thus

Using the similar method，we get

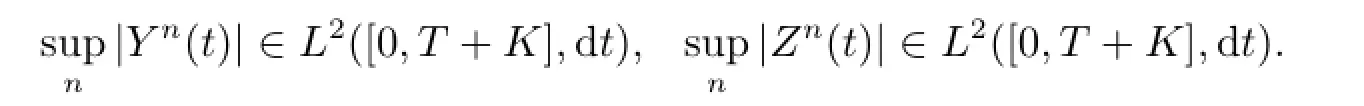
Controled convergence theorem leads to

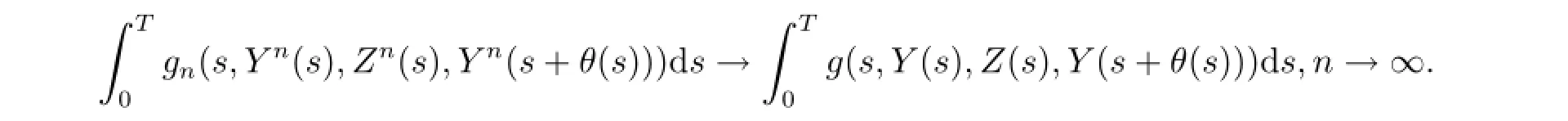
By BDG inequality，we have

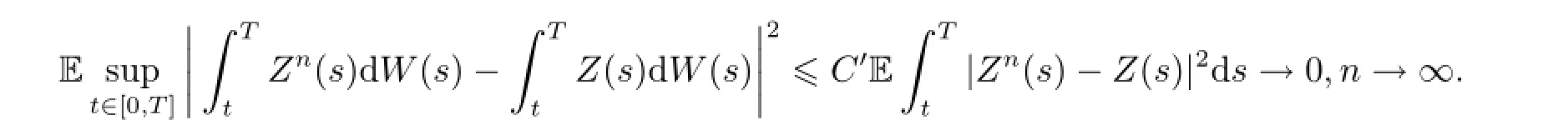
Thus there exists a subsequence，which we still denote by｛n｝such that

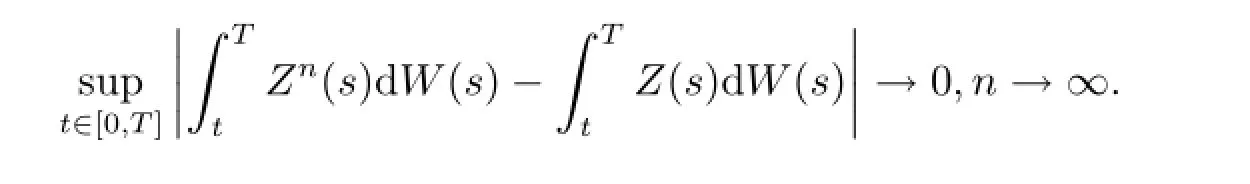
Then（Y，Z）is a solution of equation（1.2）.Now，we are going to prove Y is a minimal solution of equation（1.2）.Assume（Y＇，Z＇）is another solution of equation（1.2），by the comparison theorem in［4］，we have Y（t）≤Y＇（t）a.e.for any t∈［0，T+K］.The proof is completed.

References

［1］Aman A，N'zi M.Backward stochastic differential equations with oblique reflection and local Lipschitz drift［J］.J.Appl.Math.Stoch.Anal.，2003，16：295-309.

［2］Bahlali K.Backward stochastic differential equations with locally Lipschitz coefficient［J］.Comptes Rendus de l'Acad′emie des Sci.-Ser.I-Math.，2001，333：481-486.

［3］Lepeltier J，Martin J.Backward stochastic differential equations with continuous coeffcients［J］.Stat. Prob.Lett.，1997，32：425-430.

［4］Peng Shige，Yang Zhe.Anticipated backward stochastic differential euquations［J］.Ann.Prob.，2009，37，877-902.

［5］Hamad`ene S.Multi-dimensional BSDE with uniformly continuous coefficients［J］.Bernoulli，2003，9：571-534.

［6］Fan Shengjun，Jiang Long.Existence and uniqueness result for a backward stochastic differential equation whose generator is Lipschitz continuous in y and uniformly continuous in z［J］.J.Appl. Math.Comput.，2011，36（1）：1-10.

［7］Fan Shengjun，Ma Ming Jiang，Song Xing.On the levi type theorem for minimal solutions of bsde with continuous coefficients E［J］.J.Math.，2011，31（2）：245-250.

［8］Jia Guangyan.Some uniqueness results for one-dimensional BSDEs with uniformly continuous coefficients［J］.Stat.Prob.Lett.，2009，79（4）：436-441.

［9］Situ R.On solutions of backward stochastic differential equations with jumps and applications［J］. Stoch.Proc.Appl.，1997，66（2）：209-236.

［10］Royer M.Backward stochastic differential equations with jumps and related non-linear expectations［J］.Stoch.Proc.Appl.，1997，66：209-236.

［11］Pardoux E，Peng Shige.Adapted solution of backward stochastic differential equation［J］.Syst.Cont. Lett.，1990，4：55-61.

［12］Peng Shige.Backward stochastic differential equation and exact controllability of stochastic control systems［J］.Prog.Nat.Sci.，1994，4（3）：274-284.

［13］Peng Shige.Nonlinear expectations，nonlinear evaluations and risk measures.In stochastic methods in Finance［M］.Berlin：Lecture Notes Math.Springer，2004.

［14］Peng Shige，Xu Mingyu.Reflected BSDE with a constraint and its applications in an incomplete market［J］.Bernoulli，2010，16（3）：614-640.

一類特殊的延遲倒向隨機微分方程的最小解

凃淑恒1，廖俊俊2
（1.河南工業(yè)大學理學院，河南鄭州450002）
（2.華中科技大學數(shù)學與統(tǒng)計學院，湖北武漢430074）

本文研究一類特殊的延遲倒向隨機微分方程最小解的相關問題.當假設生成子滿足連續(xù)性假設和類似線性增長條件時，證明了最小解的存在性.本文推廣了最小解存在的一般假設條件，這里假設要弱于之前的文獻，然而本文得到了更好的引理，并且得到了相同的結論.

延遲倒向隨機微分方程；最小解；比較定理

MR（2010）主題分類號：60H99；60G99O211.63

date：2014-09-05Accepted date：2014-11-05

Supported by National Natural Science Foundation of China（10671182）.

Biography：Tu Shuheng（1986-），female，born at Xinyang，Henan，doctor，major in probability，stochastic analysis.

Liao Junjun.