ENTROPY-ULTRA-BEE SCHEME WITH A NEW ENTROPY FUNCTION FOR LINEAR ADVECTION EQUATION
CHEN Rong-san,XIAO Li,ZOU Min
(School of Mathematics and Physics,China University of Geosciences,Wuhan 430074,China)
ENTROPY-ULTRA-BEE SCHEME WITH A NEW ENTROPY FUNCTION FOR LINEAR ADVECTION EQUATION
CHEN Rong-san,XIAO Li,ZOU Min
(School of Mathematics and Physics,China University of Geosciences,Wuhan 430074,China)
In this paper,we investigate the numerical solutions for linear advection equation. A new Entropy-Ultra-bee scheme is obtained by using physical entropy function.Numerical experiments show that the scheme has a very good quality in long-time numerical computation and has high resolution in the vicinity of continuities.
linear advection equation;a new entropy function;Entropy-Ultra-bee scheme
2010 MR Subject Classification:65M08;35L65
Document code:AArticle ID:0255-7797(2016)05-0975-06
1 Introduction
The linear advection equation is of the form

where a is a constant.For any function U(u)differentiable with respect to u,it is not difficult to obtain

which show that(1.1)possesses infinitely many conservation laws,i.e.,any smooth function of u,including u itself,is conservative.
In recent years,Mao and his co-workers developed a class of finite-volume schemes for linear advection equation,see[1-8].As a scheme of the Godunov type,the schemes proceeded in the following three steps:reconstruction,evolution,cell-averaging.The entropy scheme was presented by Li and Mao in[3].In[6],Cui and Mao revealed that the entropy scheme had an error self-canceling mechanism and showed that the scheme was super-convergent. However,when computing discontinuous solutions,the scheme produced spurious oscillations near discontinuities.To fix this problem,the authors of[3]used the TVD limiter of the Ultrabee scheme to control the reconstruction step in each cell.See[9,10]or[1]for the Ultra-beescheme.The resulted scheme was thus a combination of the entropy scheme and the Ultrabee scheme.In[3],Li and Mao chose U(u)=u2as entropy function.As is known to all, physics Entropy is s=log.As a preparation for the extension of the scheme to Euler system,it needs to choose a function related to the function log.
In this paper,we follow the idea of[3]and develop a Entropy-Ultra-bee scheme with a entropy function U(u)=ulogu for linear advection equation.We presents a number of numerical examples of linear advection equation,which show that the scheme has a very good quality in long-time numerical computation and has better resolution of continuities. The organization of the paper is as follows:Section 1 is the introduction.In Section 2,we describe the scheme.In Section 3,we present three numerical examples.Section 4 is the conclusion.
2 Description of Entropy-Ultra-Bee Scheme with the New Entropy Function
We will describe Entropy-Ultra-bee scheme with the new entropy function following [1].We denote the cell size by h and use a Cartesian grid with grid cells(xj-1/2,xj+1/2)'s centered at{xj}'s,where xj±1/2=(j±1/2)h and xj=jh,j=0,±1,±2,···.We use τ to denote the time increment.The Entropy-Ultra-bee scheme is a Godunov type scheme. However,different from the other Godunov type schemes,it involves two numerical entities,the numerical solution un,which is a cell-average approximation to the true solution,
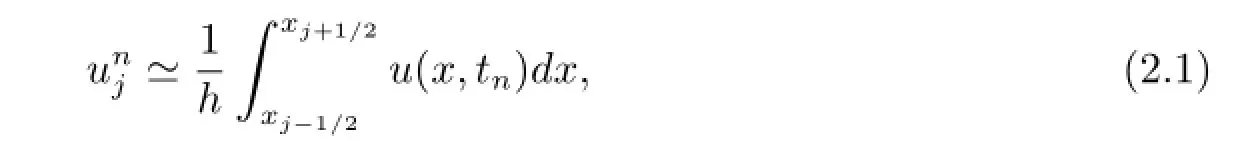
and the numerical entropy Un,which is a cell-average approximation to an entropy of the true solution,
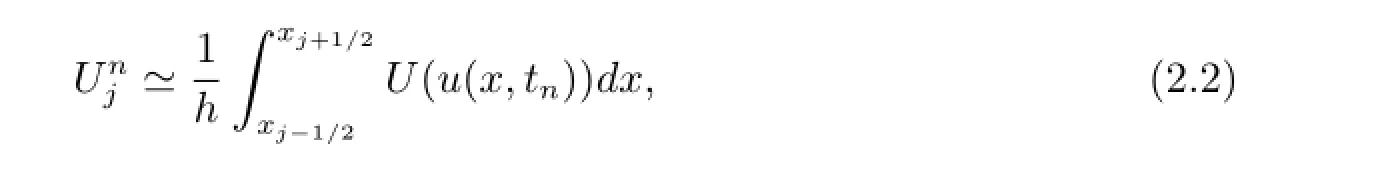
where U(u)is an entropy function of the solution.
For simplicity,we describe the scheme for(1.1)and(1.2)with a=1.As a scheme of the Godunov type,Entropy-Ultra-bee scheme with the new entropy function proceeds in the following three steps.
i)Step-ReconstructionThe solution is reconstructed in each cell as a step function involving two constant states,
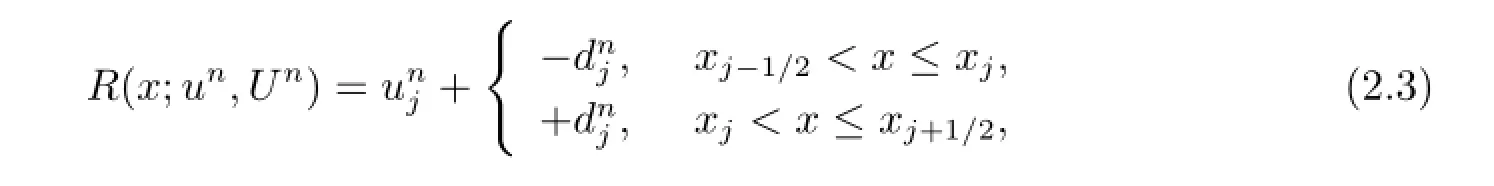
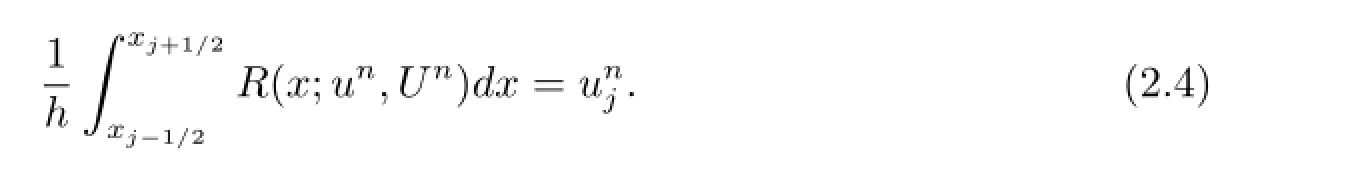
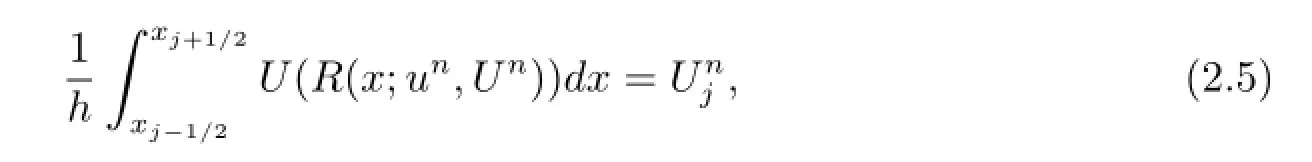
i.e.,the entropy cell-average of the reconstructed solution is equal to the numerical entropy in the cell.Equation(2.5)turns out to be an equation for
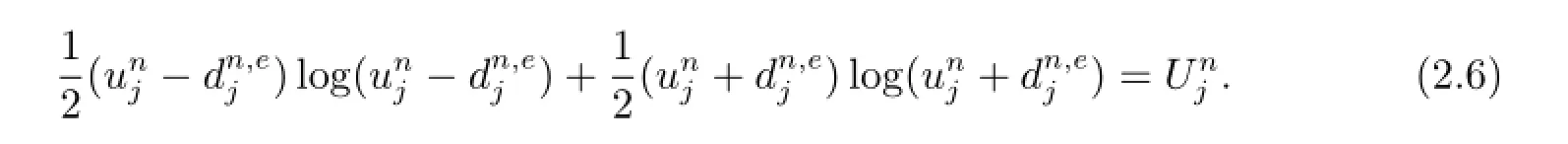
The solvability of(2.6)was discussed in§2.2 in[1],which states that the equation will have two opposite roots with the same absolute value.
The Ultra-Bee HS is computed as
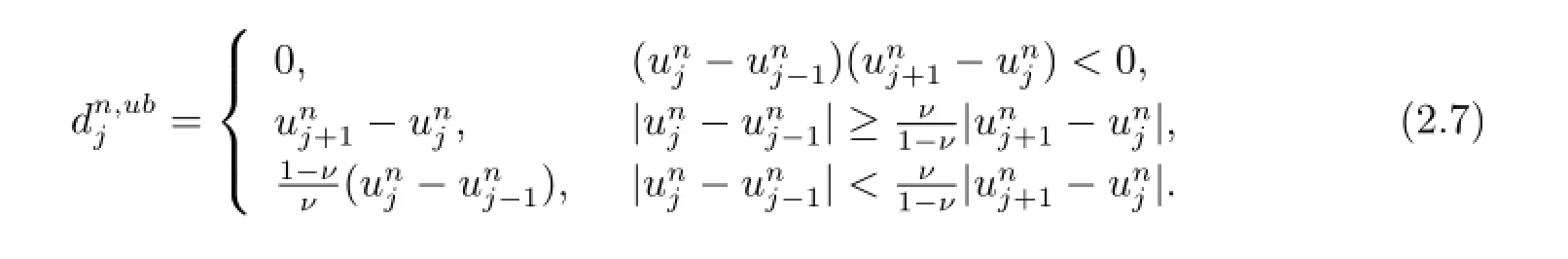
The HS is then taken as the one smaller in absolute value ofandwith the sign of
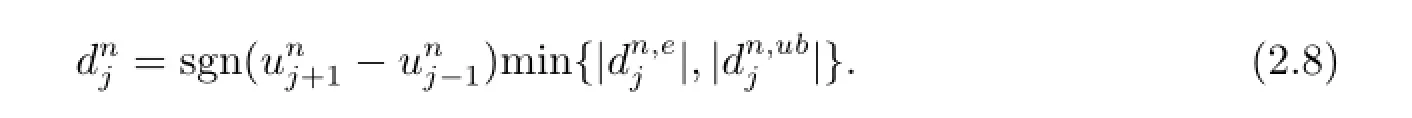
ii)EvolutionSolve the following initial value problem(IVP)
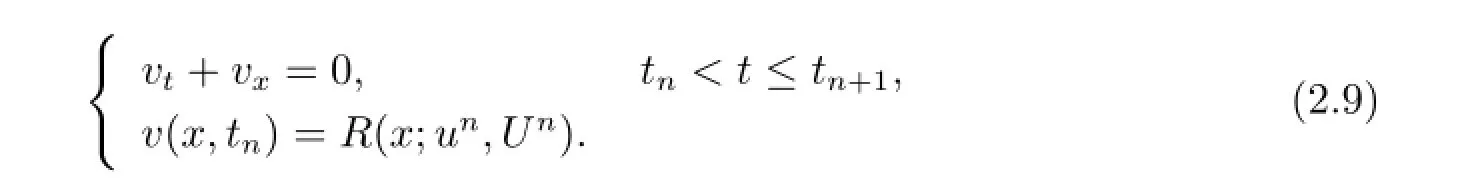
The problem can be exactly solved as
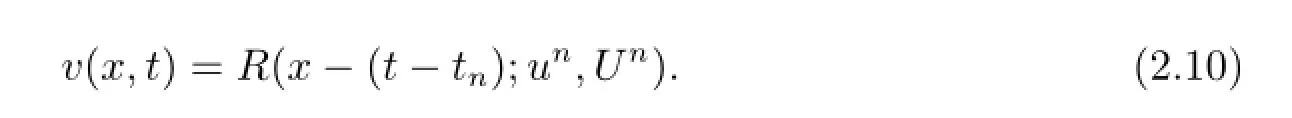
iii)Cell-averagingCompute the cell-averages of the numerical solution at t=tn+1as
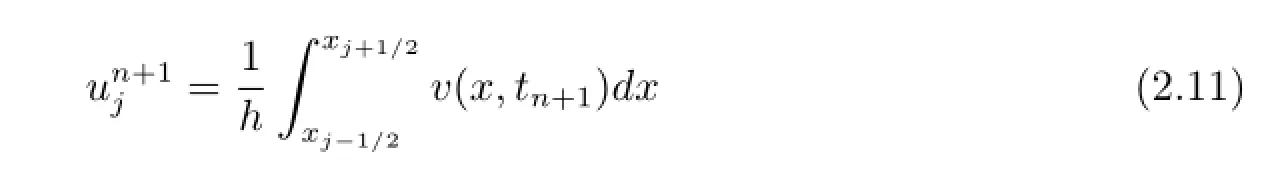
and
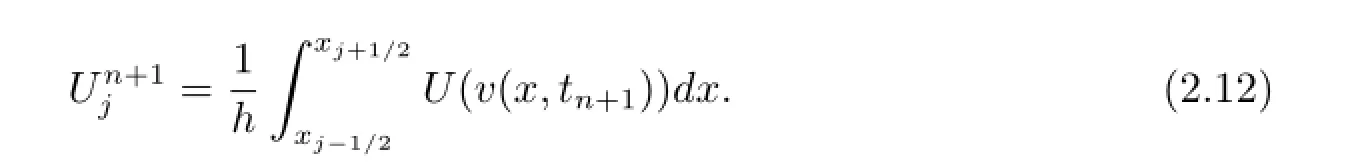
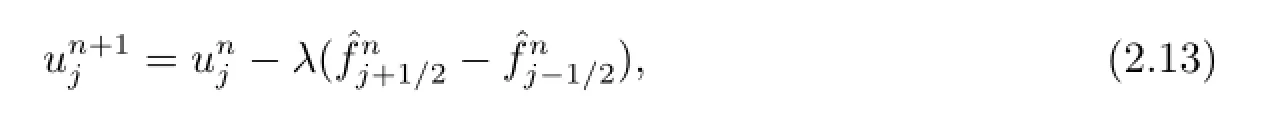
where
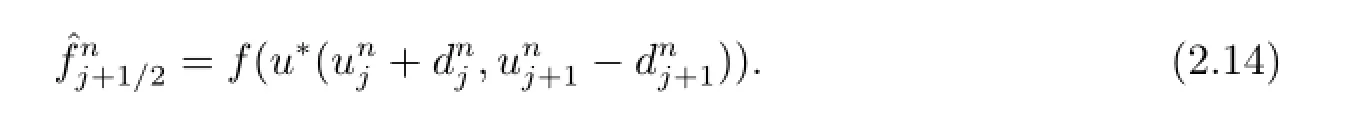
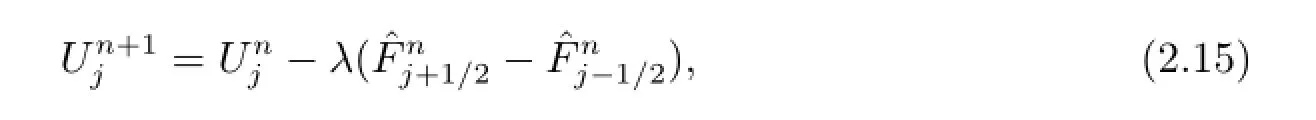
where the numerical entropy fluxis computed as
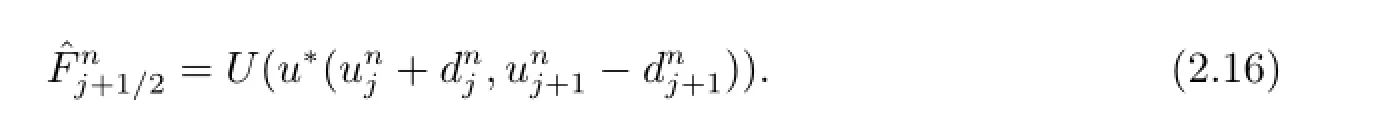
Thus we complete the description of the scheme.
3 Numerical Experiments
In this section,we will present three numerical examples to show the effectiveness of Entropy-Ultra-bee scheme with an entropy function U(u)=ulogu for linear advection equation(1.1)taking a=1.The computational domain is[0,1].To show the accuracy of the scheme,numerical solutions are compared against the true solutions.The“new”stands for the numerical solution computed by the Entropy-Ultra-bee scheme with the entropy function U(u)=ulogu.We take λ=0.45.
Example 3.1The initial value is
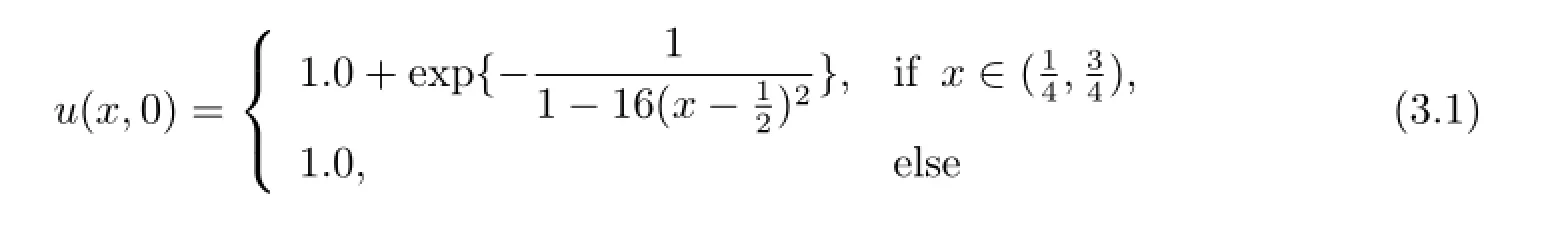
with periodic boundary conditions at the two ends.This example is come from[11].We conduct the simulation on a grid of 200 cells,up to t=1,t=10 and the numerical results are displayed in Fig.3.1.It is clearly see that the results at t=1 are in good agreement with the analytical solution.However,we notice a little defect near the corner at t=10.
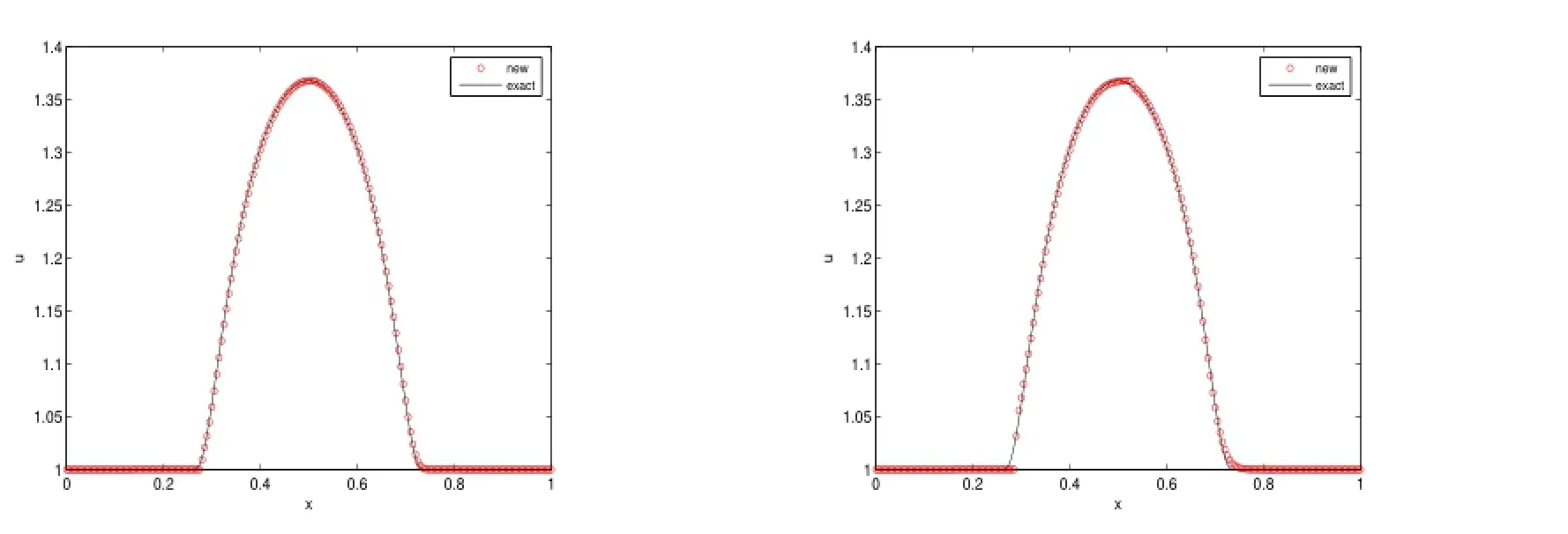
Fig.3.1:Example 3.1,200 cells,left:t=1,and right:t=10.
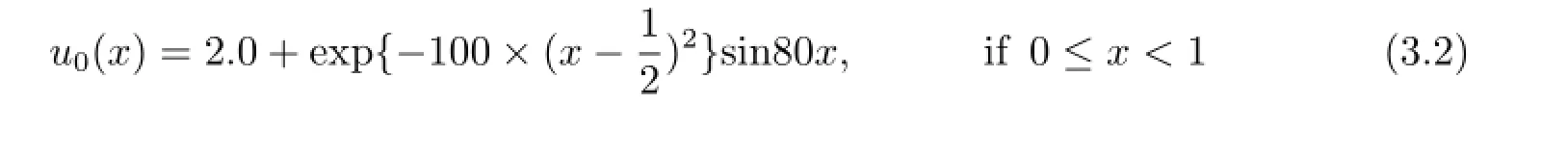
Example 3.2The initial conditions arewith periodic boundary conditions at the two ends.This example is the Wave-packet problem,see[11].This is a very challenge problem.We conduct the simulation on a grid of 200 cells,up to t=1,t=10 and the numerical results are displayed in Fig.3.2.We can see that the scheme give good results for this problem.As to our knowledge,no scheme up to date has ever got qualified numerical result for this example with the same grid beyond the time t=10.
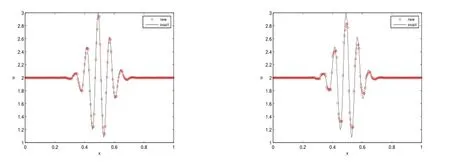
Fig.3.2:Example 3.2,200 cells,left:t=1,and right:t=10.
Example 3.3The initial value is
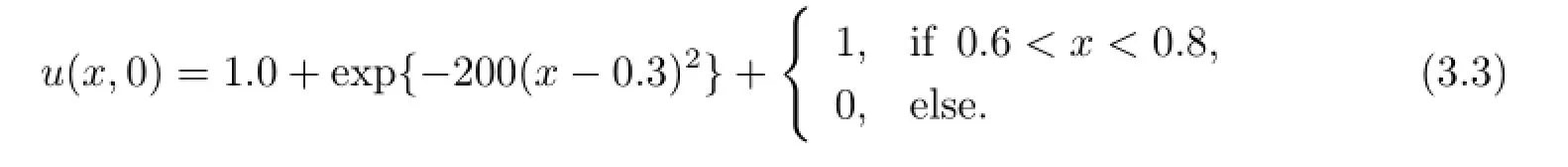
This example is come from[11].We conduct the simulation on a grid of 200 cells,up to t=1,t=10 and the numerical results are displayed in Fig.3.3.We see that the numerical solution agrees quite well with the exact one in the smooth region,all the spurious oscillations near discontinuities are eliminated and jumps are kept quite sharp with at most one transition point for each.
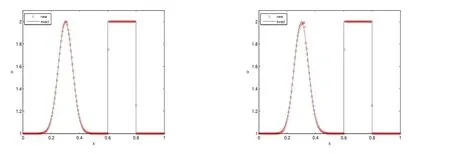
Fig.3.3:Example 3.3,200 cells,left:t=1,and right:t=10.
4 Conclusion
In this paper,we present Entropy-Ultra-bee scheme with an entropy function U(u)= ulogu for linear advection equation.Numerical experiments show that the scheme has a very good quality in long-time numerical computation and has better resolution of continuities.
References
[1]Li H X,Wang Z G,Mao D K.Numerically neither dissipative nor compressive scheme for linear advection equation and its application to the Euler system[J].J.Sci.Comput.,2008,36:285-331.
[2]Wang Z G.Finitie difference scsemes satisfying multiconservation laws for linear advection equations[D].Shanghai:Shanghai Univ.,2006(in Chinese).
[3]Li H X.Entropy dissipating scheme for hyperbolic system of conservation laws in one space dimension[D].Shanghai:Shanghai Univ.,2005(in Chinese).
[4]Wang Z G,Mao D K.Conservative difference scheme satisfying three conservation laws for linear advection equation[J].J.Shanghai University(Chinese Ed.),2006,6:588-598.
[5]Cui Y F,Mao D K.Numerical method satisfying the first two conservation laws for the Korteweg-de Vries equation[J].J.Comput.Phys.,2007,227:376-399.
[6]Cui Y F,Mao D K.Error self-canceling of a difference scheme maintaining two conservation laws for linear advection equation[J].Math.Comput.,2012,81:715-741.
[7]Chen R S,Mao D K.Entropy-TVD scheme for nonlinear scalar conservation laws[J].J.Sci.Comput.,2011,47:150-169.
[8]Chen R S,Zou M,Liu A P.Comparison of several numerical schemes for scalar linear advection equation[J].J.Math.,2015,35(4):977-982(in Chinese).
[9]Despr′es B,Lagouti`ere F.Contact discontinuity capturing schemes for linear advection and compressible gas dynamics[J].J.Sci.Comput.,2001,16:479-524.
[10]Roe P L.Some contribution to the modelling of discontinuous flows[R].Lect.Appl.Math.,1985,22:163-193.
[11]LeVeque R J.Finite Volume Methods for Hyperbolic Problems[M].Cambridge:Cambridge University Press,2002.
帶新熵函數的Entropy-Ultra-bee格式計算線性傳輸方程
陳榮三,肖莉,鄒敏
(中國地質大學(武漢)數學與物理學院,湖北武漢430074)
本文研究了線性傳輸方程的數值解法.利用物理的熵函數得到了一種新的Entropy-Ultrabee格式.數值實驗表明該格式長時間計算效果非常好,在間斷附近有比較高的分辨率.
線性發展方程;一個新的熵函數;Entropy-Ultra-bee格式
MR(2010)主題分類號:65M08;35L65O241.82
date:2015-07-07Accepted date:2015-11-03
Supported by National Natural Science Foundation of China(11201436).
Biography:Chen Rongsan(1979-),male,born at Yingshan,Hubei,associate professor,major in computational mathematics.
Xiao Li.

