GEOMETRIC TRANSIENCE FOR NON-LINEAR AUTOREGRESSIVE MODELS
SONG Yan-hong
(School of Statistics and Mathematics,Zhongnan University of Economics and Law,Wuhan 430073,China)
GEOMETRIC TRANSIENCE FOR NON-LINEAR AUTOREGRESSIVE MODELS
SONG Yan-hong
(School of Statistics and Mathematics,Zhongnan University of Economics and Law,Wuhan 430073,China)
In the paper,we study the stochastic stability for non-linear autoregressive models.By establishing an appropriate Foster-Lyapunov criterion,a sufficient condition for geometric transience is presented.
geometric transience;non-linear autoregressive model;Foster-Lyapunov criterion
2010 MR Subject Classification:60J05;60J20;37B25
Document code:AArticle ID:0255-7797(2016)05-0987-06
1 Introduction
Consider a non-linear autoregressive Markov chainondefined by
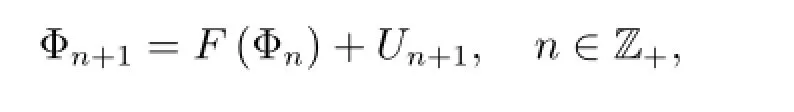
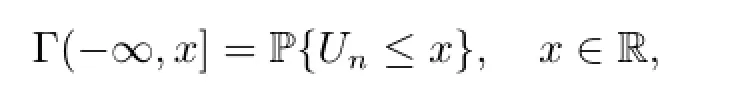
First,let us recall some notations and definitions,see[3,5,6]for details.Denote by)the Borel σ-field on R,and write=.The n-steptransition kernel of the chain Φnis defined as
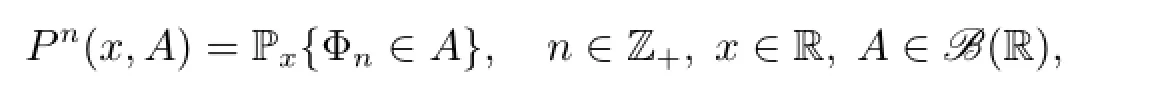
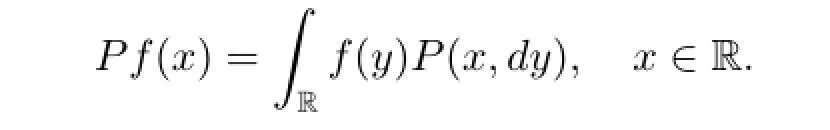
The chain Φnis Lebesgue-irreducible,if for every
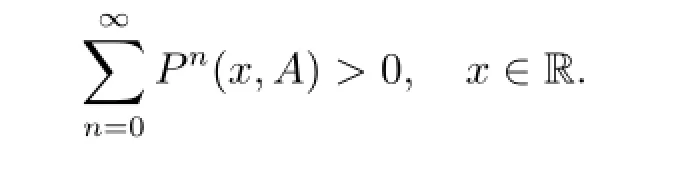
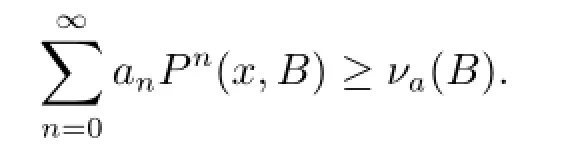
Obviously,the subset of a petite set is still petite.By[7,Lemma 2.1]or[8,Theorem 1],we know that the non-linear autoregressive model is Lebesgue-irreducible,and every compact set inis petite.
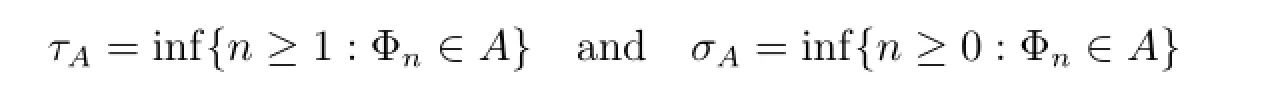
be the first return and first hitting times,respectively,on A.It is obvious that τA=σAif Φ0∈Ac.Denote by L(x,A)=the probability of the chain Φnever returning to A.
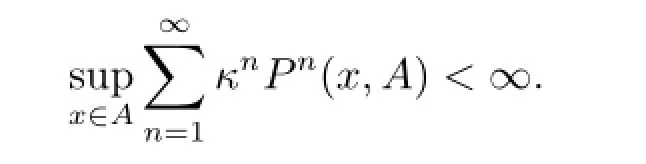
The chain Φnis called geometrically transient,if it is ψ-irreducible for some non-trivial measure ψ,and R can be covered ψ-a.e.by a countable number of uniformly geometrically transient sets.That is,there exist sets D and Ai,i=1,2,···such that=D∪where ψ(D)=0 and each Aiis a uniformly geometrically transient set of the chain Φn.
To state the main result of this paper,we need the following assumptions:
Theorem 1.1Assume(A1)and(A2).Then the non-linear autoregressive model Φnis geometrically transient.
Remark 1.2It is easy to see that(A2)is equivalent to the condition in[9,Theorem 3.1],where transience for the the non-linear autoregressive model Φnwas confirmed.Here,we get a stronger result(i.e.geometric transience)in Theorem 1.1.
2 Proof of Theorem 1.1
This section is devoted to proving Theorem 1.1 by using the Foster-Lyapunov(or drift)condition for geometric transience.
It is well known that Foster-Lyapunov conditions were widely used to study the stochastic stability for Markov chains.For examples,Down,Meyn and Tweedie[10-13]studied the drift conditions for recurrence,ergodicity,geometric ergodicity and uniform ergodicity.The drift conditions for sub-geometric ergodicity were discussed in[1,4,14-17]and so on.In [18,19],the drift conditions for transience were obtained.
Recently,we investigated the drift condition for geometric transience in[6].One of the main results shows that the chain Φnis geometrically transient,if there exist some set,constants λ,b∈(0,1),and a function W≥1A(with W(x0)<∞for somesatisfying the drift condition
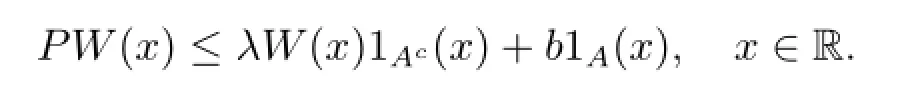
As far as we know,however,this drift condition can not be applied directly for the nonlinear autoregressive model considered in this paper.Alternatively,we will establish a more practical drift condition for geometric transience.First,we need the following two lemmas,which are taken from[6].
Lemma 2.1The chain Φnis geometrically transient if and only if there exist someand a constant κ>1 such that
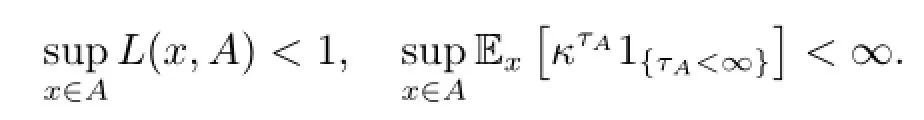
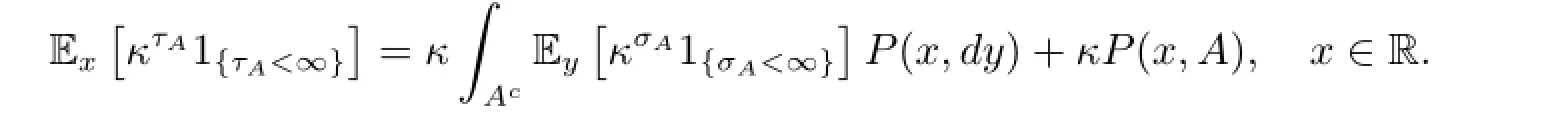
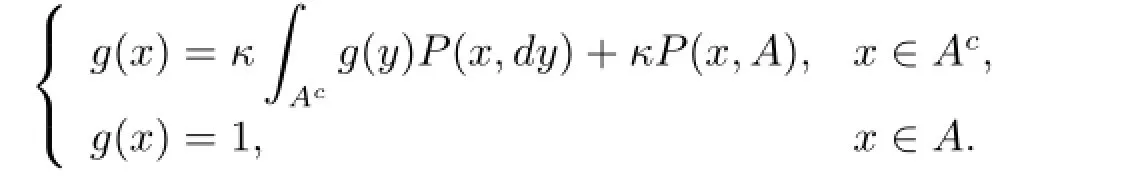
Proposition 2.3The chain Φnis geometrically transient,if there exist a petite set,constants λ∈(0,1),b∈(0,∞),and a non-negative measurable function W bounded on A satisfying
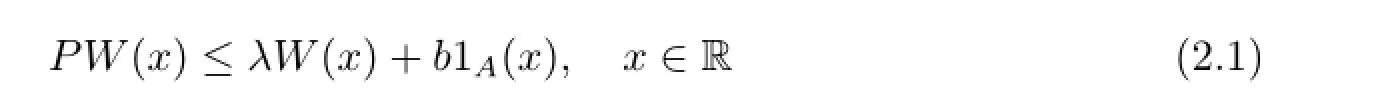
and
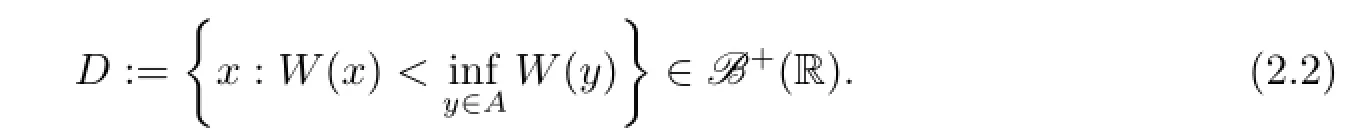
ProofSince W is non-negative and),we have.Set
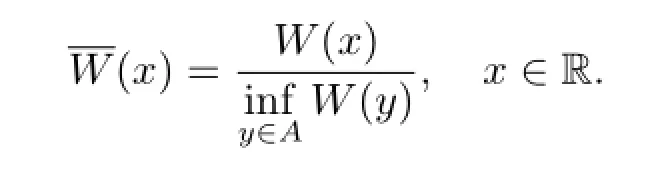
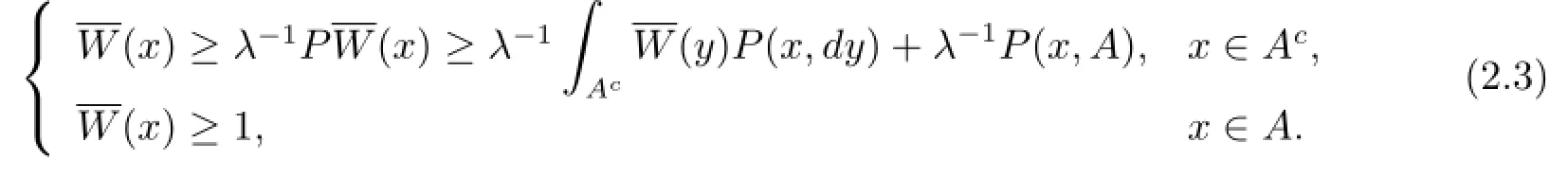
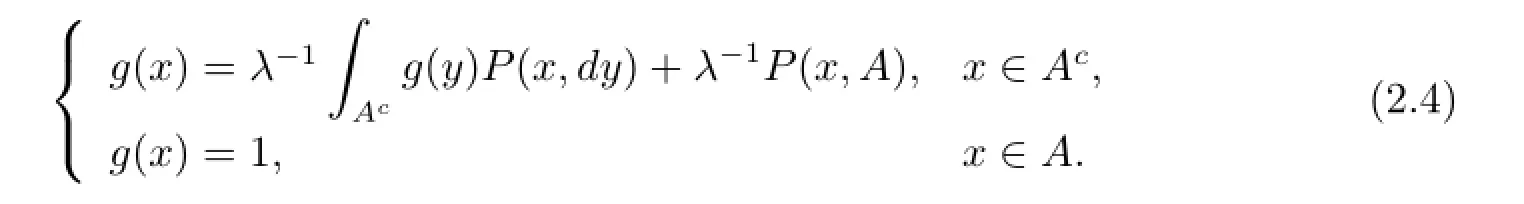
Hence by the comparison theorem of the minimal non-negative solution(see[20,Theorem 2.6]),we know from(2.3)and(2.4)that
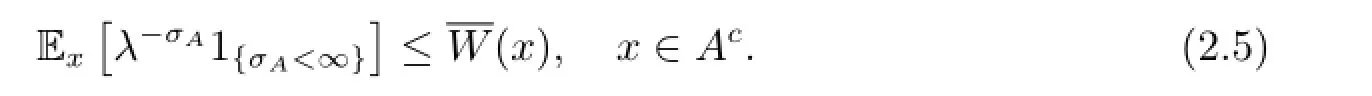
By(2.5)and noting that D?Ac,we have for all x∈R,
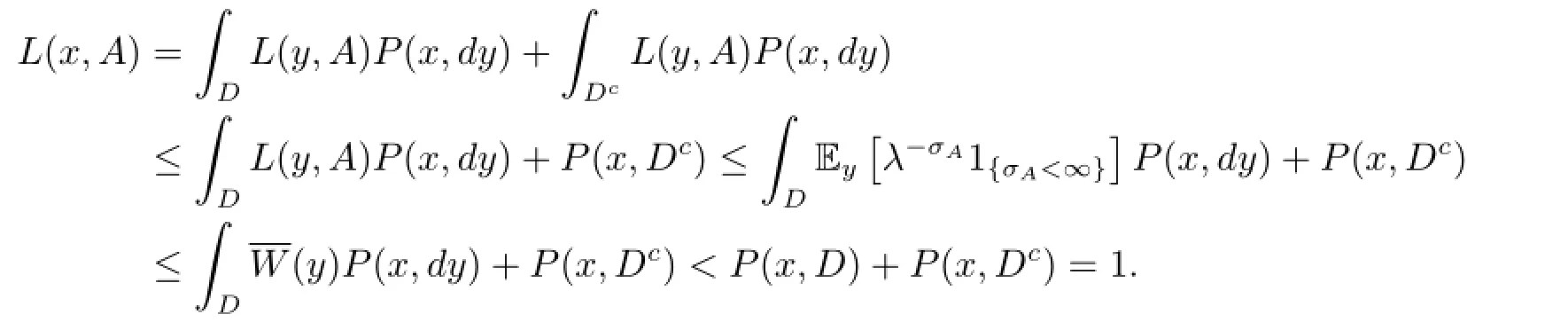
Thus there exists some set C?A withsuch that

According to Lemma 2.1,in the following,it is enough to prove that for some κ>1,
Combining Lemma 2.2(1)with(2.5)and(2.1),we get for all x∈A,
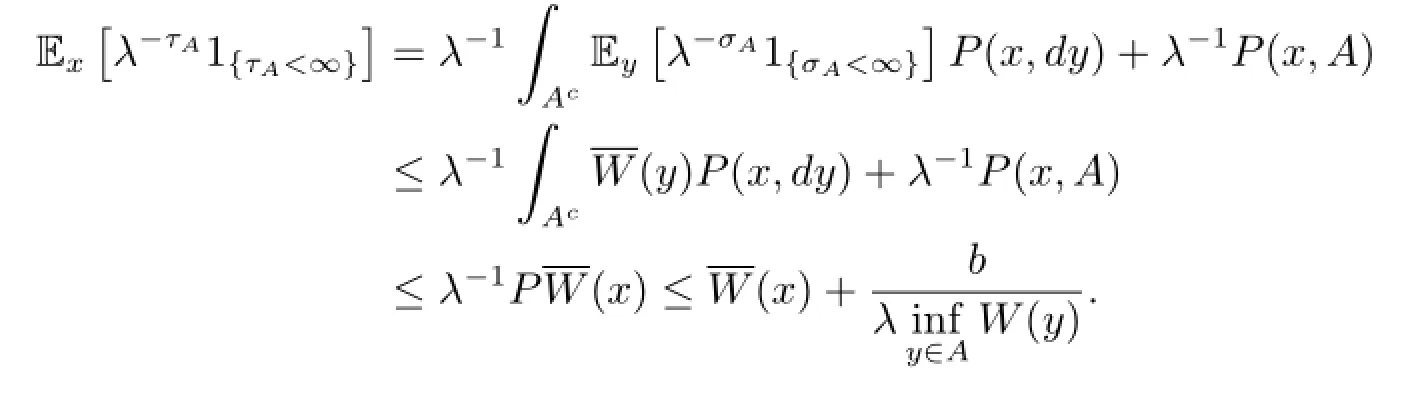
Since W is bounded on A,

Noting that A is petite and C?A,according to(2.7)and the proof of[3,Theorem 15.2.1],we obtain that for all 1<κ≤λ-1/2<∞.This together with(2.6) yields the desired assertion.
Now,we are ready to prove Theorem 1.1.
Proof of Theorem 1.1By(A2),there exist constants θ>0 and c>0 satisfying
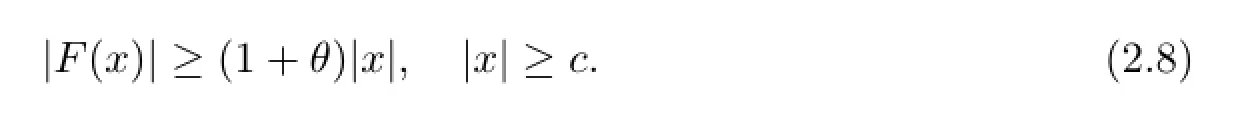
Choose
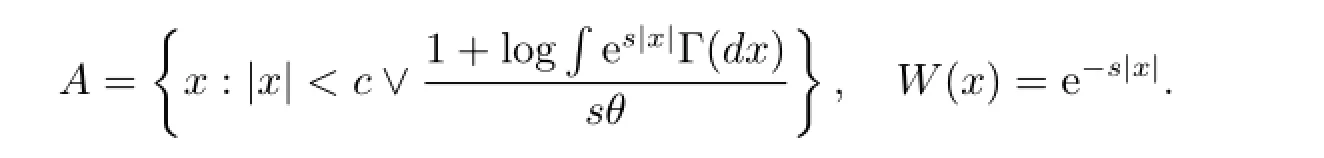
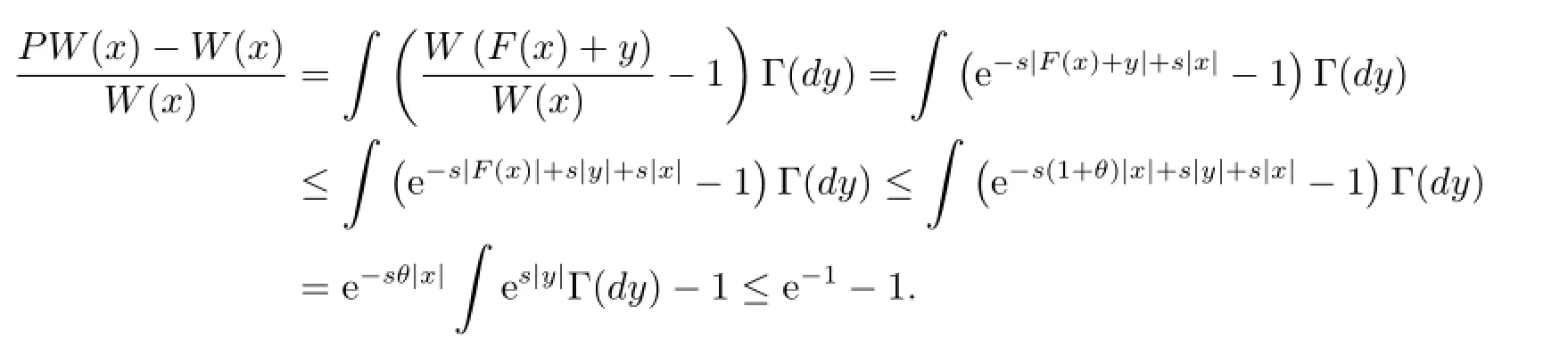
That is,
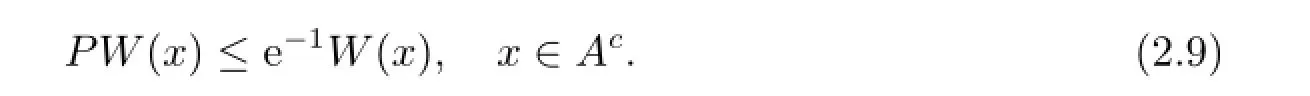
Noting that W is bounded,it is obvious that for some b∈(0,∞),
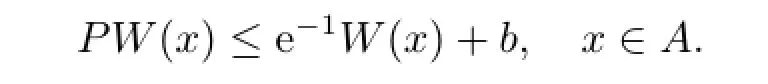
Combining this with(2.9),the drift condition(2.1)holds.Thus the non-negative autoregressive model Φnis geometrically transient by Proposition 2.3.
References
[1]Douc R,Fort G,Moulines E,Soulier P.Practical drift conditions for subgeometric rates of convergence[J].Ann.Appl.Prob.,2004,14(3):1353-1377.
[2]Fort G,Moulines E.Polynomial ergodicity of Markov transition kernels[J].Stoch.Proc.Appl.,2003,103(1):57-99.
[3]Meyn S P,Tweedie R L.Markov chains and stochastic stability(2nd ed.)[M].London:Springer-Verlag,1993.
[4]Tuominen P,Tweedie R L.Subgeometric rates of convergence of f-ergodic Markov chains[J].Adv. Appl.Prob.,1994,26(3):775-798.
[5]Gao Zhenlong,Wang Weigang,Hu Dihe.The convergence for transition functions of Markov chains in random environments[J].J.Math.,2008,28(5):546-550.
[6]Mao Yonghua,Song Yanhong.On geometric and algebraic transience for discrete-time Markov chians[J].Stoch.Proc.Appl.,2014,124(4):1648-1678.
[7]An H Z,Huang F C.The geometrical ergodicity of nonlinear autoregressive models[J].Stat.Sinica,1996,6:943-956.
[8]Bhattacharya R,Lee C.On geometric ergodicity of nonlinear autoregressive models[J].Stat.Prob. Lett.,1995,22(4):311-315.
[9]Lee O.Geometric ergodicity and transience for nonlinear autoregressive models[J].Comm.Korean Math.Soc.,1995,10(2):409-417.
[10]Down D,Meyn S P,Tweedie R L.Exponential and uniform ergodicity of Markov processes[J].Ann. Prob.,1995,23(4):1671-1691.
[11]Meyn S P,Tweedie R L.Stability of Markovian processes I:criteria for discrete-time chains[J].Adv. Appl.Prob.,1992,24(3):542-574.
[12]Meyn S P,Tweedie R L.Stability of Markovian processes II:continuous time processes and sampled chains[J].Adv.Appl.Prob.,1993,25(3):487-517.
[13]Meyn S P,Tweedie R L.Stability of Markovian processes III:Foster-Lyapunov criteria for continuous time processes[J].Adv.Appl.Prob.,1993,25(3):518-548.
[14]Jarner S F,Roberts G O.Polynomial convergence rates of Markov chains[J].Ann.Appl.Prob.,2002,12(1):224-247.
[15]Mao Yonghua.Algebraic convergence for discrete-time ergodic Markov chains[J].Sci.China Ser.A,2003,46(5):621-630.
[16]Mao Yonghua.Ergodic degrees for continuous-time Markov chains[J].Sci.China Ser.A,2004,47(2):161-174.
[17]Fort G,Roberts G O.Subgeometric ergodicity of strong Markov processes[J].Ann.Appl.Prob.,2005,15(2):1565-1589.
[18]Stramer O,Tweedie R L.Stability and instability of continuous time Markov processes[C].Chichester:Wiley,Prob.,Stat.Optim.,1994:173-184.
[19]Tweedie R L.Criteria for classifying general Markov chians[J].Adv.Appl.Prob.,1976,8(4):737-771.
[20]Chen Mufa.From Markov chains to non-equilibrium particle systems(2nd ed.)[M].Singapore:Word Sci.,2004.
非線性自回歸模型的幾何非常返性
宋延紅
(中南財經政法大學統計與數學學院,湖北武漢430073)
本文研究了非線性自回歸模型的隨機穩定性.通過建立恰當的Foster-Lyapunov條件,得到了非線性自回歸模型幾何非常返的充分條件.
幾何非常返;非線性自回歸模型;Foster-Lyapunov條件
MR(2010)主題分類號:60J05;60J20;37B25O211.62;O211.9
date:2016-03-11Accepted date:2016-06-01
Supported by National Natural Science Foundation of China(11426219;11501576).
Biography:Song Yanhong(1983-),female,born at Yantai,Shandong,lecturer,major in probability.

