導彈折疊翼展開過程的動力學仿真及試驗研究

甄文強，姬永強，石運國

（中國工程物理研究院總體工程研究所，四川綿陽621000）

導彈折疊翼展開過程的動力學仿真及試驗研究

甄文強，姬永強，石運國

（中國工程物理研究院總體工程研究所，四川綿陽621000）

對導彈中常用的橫向折疊翼展開過程進行研究，考慮折疊翼展開過程中氣動阻力和摩擦力的作用，建立了導彈發射及地面試驗時折疊翼展開過程的數學模型，使用動力學仿真軟件建立相應動力學仿真模型，設計并制作了折疊翼，使用高速攝影獲取折疊翼展開過程圖像，開展地面試驗研究。研究結果表明，試驗結果與數學模型及動力學仿真模型結果的一致性較好，驗證了折疊翼展開過程數學及動力學仿真模型的正確性。根據試驗結果給出摩擦力矩的具體取值范圍，為折疊翼的工程設計和應用提供了參考。

兵器科學與技術；折疊翼；展開；動力學仿真；試驗

0 引言

導彈一般使用折疊翼面來縮小其橫向尺寸，以節省導彈的儲運空間，便于導彈的箱式儲裝、運輸和發射，同時增加車輛或艦艇的運載能力［1］。按折疊方向分類，折疊翼可以分為橫向折疊式和縱向折疊式。前者是在翼面根部或中部沿彈體軸向設置一分離面，安裝轉軸，使外翼部分可繞軸折疊和展開，一般使用扭桿、扭簧等作為動力來源，多用于中小型導彈的彈翼結構中。橫向折疊式彈翼折疊狀態不占用彈內空間、展開及鎖緊機構緊湊，獲得了較為廣泛的應用［2-3］。圖1給出了橫向折疊翼展開過程的折疊狀態、展開過程及鎖緊狀態。

圖1　折疊翼的不同狀態Fig.1 Different states of folding-wing

針對折疊翼的展開過程，國內外學者開展了大量的研究。李莉等［4］、崔二巍等［5］、趙俊鋒等［6］均使用Adams軟件建立了燃氣驅動式縱向折疊翼展開的動力學模型，并進行了優化分析；吳俊全等［7］開展了縱向折疊翼試驗和仿真工作，對比分析了試驗和仿真結果，為折疊翼設計提供了指導；張欽等［8］、胡文華等［9］、雷歌等［10］針對無人機及水下潛航器的折疊翼進行了機構設計和動力學仿真工作；秦永明等［11］、賈毅等［12］則分別從氣動和試驗技術的角度針對折疊翼的地面試驗展開了相關的研究工作，取得了一定的進展；李真等［13］則使用計算流體力學（CFD）方法對折疊翼展開過程進行模擬，為折疊翼設計提供參考。目前，針對橫向折疊翼的展開過程，還沒有學者結合數學模型、動力學仿真模型及試驗開展工作。尤其是沒有針對折疊翼展開過程中外翼受到的氣動阻力和摩擦力展開分析。

本文主要從數學模型、動力學仿真模型和地面試驗3個角度對折疊翼的展開過程進行分析。建立了考慮氣動阻力和摩擦影響的數學模型，并使用軟件建立了考慮鎖緊裝置影響的展開動力學模型。通過開展試驗研究，并與數學模型和動力學仿真模型進行對比分析，同時分析了氣動阻力和摩擦力對展開過程的影響。研究結果表明，建立的數學及動力學仿真模型與試驗結果吻合較好，明確了氣動阻力和摩擦力對折疊翼展開過程的影響，給出了摩擦力矩的取值范圍，為折疊翼的工程設計提供了參考。

1 折疊翼展開過程的數學模型

1.1導彈發射時折疊翼展開過程的數學模型

導彈發射前，折疊翼被翼軌約束并折疊于發射箱內，折疊翼驅動扭桿處于預扭轉狀態；導彈發射離箱后，約束解除，外翼在扭桿作用下繞轉軸轉動，在接近鎖緊位置時，鎖緊裝置動作，將外翼與內翼鎖緊。

在展開過程中，外翼的運動微分方程為

圖2　外翼展開示意圖Fig.2 Deployment of outboard wing

由于導彈離箱時速度較低且處于零攻角狀態，因此氣動阻力主要是指外翼轉動過程中受到的垂直于翼面阻礙翼面轉動的氣動阻力。在折疊翼展開過程中，發動機推力沿折疊翼轉軸方向，不會產生在轉軸方向的力矩，對折疊翼展開過程沒有影響；而且，導彈與折疊翼同時受到重力作用，在重力方向產生相同的加速度，以導彈為參考系，研究折疊翼展開過程可以不考慮重力影響。于是有

式中:扭桿產生的力矩為

GIp為扭桿的抗扭剛度，G為扭桿材料的剪切模量，Ip為扭桿的截面極慣性矩，L為扭桿長度，θ0是扭桿的預扭角度。

外翼轉動時受到的氣動阻力可使用工程方法進行計算，沿展向積分得到氣動阻力的力矩為

式中:ρ為空氣密度；c為氣動阻力系數；Lx為外翼弦長；lw為外翼展長。

將（2）式～（4）式代入（1）式，整理得

（5）式即為發射過程中折疊翼展開過程的數學模型。通過求解該方程，可以得到外翼轉動的角度θ、角速度ω=θ·隨時間的變化關系。

使用數值方法求解（5）式，可以得到外翼轉動的角度θ隨時間的變化關系，如圖3所示。

圖3　外翼轉動角度隨時間的變化關系Fig.3 Torque angle versus deployment time

圖3給出了不同的氣動阻力系數c和摩擦力矩Mf時的轉角與時間曲線。從中可以看到:

1）氣動阻力系數和摩擦力矩越大，折疊翼展開的時間越長；

2）在c=0、Mf=0時，展開時間最短為0.145s；

3）氣動阻力系數和摩擦力矩對曲線的影響隨時間逐漸變大。這一方面是因為扭桿產生的力矩Md逐漸變小，氣動及摩擦阻力影響相對逐漸變大；另一方面是因為氣動阻力隨外翼轉動速度逐漸變大，進一步增大了其對展開時間的影響。

1.2地面試驗時折疊翼展開的數學模型

不同于發射過程，在進行折疊翼地面試驗時，折疊翼的外翼固定于地面，需考慮重力對外翼展開過程的影響，在試驗過程中，折疊翼內翼與地面垂直，折疊狀態時外翼與地面呈45°夾角。在考慮重力的影響后，（5）式修正為

式中:m為外翼的質量；g為重力加速度、L0為外翼質心到轉軸的距離。通過（6）式可以得到試驗過程中重力對展開過程的影響（見圖4）。

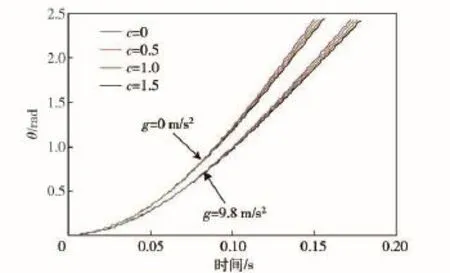
圖4　外翼轉動角度隨時間的變化關系Fig.4 Torque angle versus deployment time

從圖4中可以看到，相對于氣動阻力，重力對展開時間的影響更為明顯，顯著增大了折疊翼展開到位的時間。

2 折疊翼展開過程的動力學仿真模型

2.1動力學仿真模型

在計算機輔助設計CAD軟件中建立折疊翼的三維模型，導入動力學仿真軟件中，建立折疊翼展開和鎖緊過程的動力學仿真模型。

在動力學模型中，內翼施加固定約束，外翼和外翼轉軸與內翼間施加轉動副；鎖緊裝置與內翼間施加滑動副及彈簧，鎖緊裝置與外翼間施加接觸條件；根據（2）式和（3）式，可以在外翼轉軸方向上施加扭桿的扭矩和氣動阻力的力矩，分別與外翼的轉動角度和角速度有關；同時在外翼轉軸方向施加摩擦力矩。模型如圖5所示。

圖5　折疊翼的動力學仿真模型Fig.5 Dynamic simulation model of folding-wing

2.2導彈發射過程的動力學仿真模型結果對比

對上述動力學模型進行仿真分析，可以得到外翼轉動的角度及角速度隨時間的變化關系（見圖6），并與數學模型的結果進行對比。

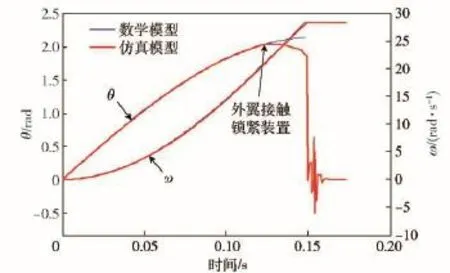
圖6　外翼轉動角度及角速度隨時間的變化關系Fig.6 Torque angle and angular velocity

圖6給出的是發射過程中，在不考慮重力、氣動阻力和摩擦力的情況下，數學模型與動力學仿真模型得到的外翼轉動角度和角速度隨時間變化的曲線。由圖6可以看到:兩個模型得到的曲線吻合較好；在0.13s左右，動力學仿真模型得到的角速度出現下降，并在0.15s左右迅速下降至0附近振蕩，其原因是鎖緊裝置開始接觸外翼并鎖緊。

上述曲線表明，數學模型結果與動力學仿真模型的結果吻合較好，動力學仿真模型可以仿真鎖緊過程，相對更接近工程實際。

2.3地面試驗過程的動力學仿真模型結果對比

在動力學仿真模型中考慮重力和摩擦的影響，并將仿真結果與數學模型結果進行對比分析，如圖7所示。

圖7　外翼轉動角度隨時間的變化關系Fig.7 Torque angle versus deployment time

通過分析重力和摩擦對展開過程的影響對比，進一步明確數學模型和動力學仿真模型一致性較好；通過圖7可以看到:曲線的后段出現差別，動力學仿真模型的折疊翼展開到位時間更長，這是因為在鎖緊過程中，外翼與鎖緊裝置碰撞并驅動其回退，需要消耗外翼的動能，導致其角速度減小，使得時間延長；而且，重力的作用和摩擦力矩的增大使得該差別變大，是因為重力的作用和摩擦力矩的增大減小了外翼具有的動能，使得鎖緊裝置消耗能量的影響相對更加顯著。

3 折疊翼展開過程的試驗研究

3.1試驗過程

將折疊翼內翼固定于臺鉗上，內翼與地面垂直，使用高速攝影沿翼弦方向捕捉展開過程的圖像。將外翼旋轉至折疊狀態，啟動高速攝影，解除外翼約束，外翼在扭桿的扭矩作用下迅速展開，在接近鎖緊位置時，鎖緊裝置動作，將外翼與內翼鎖緊。

圖8給出的是高速攝影獲取的折疊翼展開圖像，使用Matlab編寫圖像處理程序，捕捉外翼的翼尖、轉軸及內翼的固定位置，可以得到每一幀圖像中折疊翼外翼與內翼間的夾角δ，如圖8（a）和圖8（b）所示。于是，試驗得到的外翼轉動角度為θ=δ-（π-θw）.

3.2試驗結果對比分析

地面試驗共進行兩次，經數據處理后得到外翼轉動角度隨時間的變化曲線，如圖9所示。

由圖9可以看到，兩次試驗得到的曲線幾乎完全重合，試驗數據的分散性很小，表明試驗結果的正確性和可靠性較高。

下面將試驗得到的曲線與數學模型得到的曲線進行對比。圖10給出了氣動阻力系數和摩擦力矩取典型值時，外翼轉角與時間曲線和試驗結果曲線的對比情況。

從圖10的曲線可以看出，試驗結果曲線與數學模型得到的曲線形式基本一致，在氣動阻力系數和摩擦力矩的合理取值范圍內，數學模型得到的曲線分布在試驗曲線附近。

為了進一步分析氣動阻力系數和摩擦力矩對折疊翼展開過程的影響，需要考察數學模型的結果曲線f（t）和試驗結果曲線g（t）的接近程度。

取任意轉動角度θ，則兩條曲線分別對應時間t1=f-1（θ），t2=g-1（θ），定義r表征曲線的接近程度:

r越小，說明曲線越接近。

圖8　折疊翼展開過程高速攝影圖像Fig.8 Photos of the folding-wing deployment

圖9　外翼轉動角度隨時間的變化關系Fig.9 Torque angle versus deployment time

于是，可以得到r與氣動阻力系數c和摩擦力矩Mf的關系，如圖11所示。

圖11中繪制了氣動阻力系數c從0線性變化至3時，試驗結果與數學模型結果曲線的接近程度r隨摩擦力矩的變化趨勢。由圖11可以得到:

1）在Mf小于臨界值時，r與c呈負相關關系；在Mf大于臨界值時，r與c呈正相關關系。

2）對于任意c，Mf均有最小值。工程上，在c取合理區間0.5～2時，Mf合理取值范圍約為2.7～3.7N·m.

圖10　外翼轉動角度隨時間的變化關系Fig.10 Torque angle versus deployment time

圖11　r隨氣動阻力系數c、摩擦力矩Mf的關系Fig.11 r versus c and Mf

4 結論

1）針對導彈發射時折疊翼的展開過程，建立了考慮氣動阻力和摩擦力的數學模型；針對折疊翼的地面試驗，建立了考慮氣動阻力、摩擦力及重力的數學模型。

2）使用動力學仿真軟件建立了折疊翼展開的動力學仿真模型，對折疊翼在導彈發射、地面試驗時的展開過程和鎖緊過程進行仿真。仿真結果均與數學模型的結果吻合較好，在外翼接觸鎖緊裝置時，外翼角速度出現明顯減小，相比數學模型更接近工程實際。

3）通過地面試驗，獲得了折疊翼展開過程的圖像，并通過編寫圖像處理程序得到折疊翼轉動角度隨時間的變化曲線。在摩擦力矩和氣動阻力系數取合理的數值時，試驗結果與數學模型及仿真模型的結果較為吻合。

4）分析了摩擦力矩和氣動阻力系數對折疊翼展開過程的影響，得到了摩擦力矩Mf的合理取值范圍為2.7～3.7N·m，可以為折疊翼的工程設計提供參考。

（References）

［1］ 余旭東，葛金玉，段德高，等.導彈現代結構設計［M］.北京:國防工業出版社，2007. YU Xu-dong，GE Jin-yu，DUAN De-gao，et al.Modern structure design of missiles［M］.Beijing:National Defense Industry Press，2007.（in Chinese）

［2］ Kroyer R.Wing mechanism analysis［J］.Computers and Structures，1999，72（2）:253-265.

［3］ Henry J I，Schwartz D R，Soukup M A.Design construction and testing of a folding-wing tube-launched micro air vehicle［C］∥43rd AIAA Aerospace Sciences Meeting and Exhibit.Reno，Nevada:AIAA，2005:2005-1451.

［4］ 李莉，任茶仙，張鐸.折疊翼機構展開動力學仿真及優化［J］.強度與環境，2007，34（1）:17-21. LI Li，REN Cha-xian，ZHANG Duo.Dynamic simulation and optimization design of deployment of folding-wing［J］.Structure& Environment Engineering，2007，34（1）:17-21.（in Chinese）

［5］ 崔二巍，于存貴，李猛，等.某導彈折疊彈翼展開過程的仿真分析［J］.兵工自動化，2013，32（12）:12-14. CUI Er-wei，YU Cun-gui，LI Meng，et al.Simulation analysis of a missile folding wing deployment process［J］.Ordnance Industry Automation，2013，32（12）:12-14.（in Chinese）

［6］ 趙俊鋒，劉莉，楊武，等.折疊彈翼展開動力學仿真及優化［J］.彈箭與制導學報，2012，32（2）:155-157. ZHAO Jun-feng，LIU Li，YANG Wu，et al.Dynamic simulation and optimization design of folding wing deployment［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2012，32（2）: 155-157.（in Chinese）

［7］ 吳俊全，孫海文，張曉旻.折疊翼展開試驗與動力學仿真研究［J］.彈箭與制導學報，2011，32（3）:164-166. WU Jun-quan，SUN Hai-wen，ZHANG Xiao-min.The research on unfolding test and dynamic model of folding-wing［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2011，32（3）: 164-166.（in Chinese）

［8］ 張欽，聶宏，張明，等.無人機折疊翼展開動力學分析［J］.機械設計與制造工程，2015，44（2）:12-16. ZHANG Qin，NIE Hong，ZHANG Ming，et al.Dynamic analysis of UAV folding wing depolyment process［J］.Machine Design and Manufacturing Engineering Technology，2015，44（2）:12-16.（in Chinese）

［9］ 胡文華，張偉，曹東興.折疊翼的理論建模與實驗研究［J］.動力學與控制學報，2015，13（3）:230-234. HU Wen-hua，ZHANG Wei，CAO Dong-xing.Research on theoretical model and experiments of folding wings［J］.Journal of Dynamics and Control，2015，13（3）:230-234.（in Chinese）

［10］ 雷歌，鄧飛，劉權，等.水下航行器折疊翼展開機構設計與動力學仿真［J］.魚雷技術，2013，21（2）:81-85. LEI Ge，DENG Fei，LIU Quan，et al.Design and dynamic simulation of folding wing expansion mechanism of underwater vehicle［J］.Torpedo Technology，2013，21（2）:81-85.（in Chinese）

［11］ 秦永明，蔡琛芳，董金剛.機載導彈折疊舵展開氣動特性試驗研究［J］.航空兵器，2013（5）:3-6. QIN Yong-ming，CAI Chen-fang，DONG Jin-gang.Experimental study on aerodynamics of airborne missile folding rudder［J］. Aero Weaponry，2013（5）:3-6.（in Chinese）

［12］ 賈毅.戰術導彈折疊翼兩種展開方法及測試結果比較［J］.流體力學實驗與測量，2003，17（2）:70-73. JIA Yi.The comparison between two deploying methods and results of folding wings for some tactical missiles［J］.Experiments and Measurements in Fluid Mechanics，2003，17（2）:70-73.（in Chinese）

［13］ 李真，董玉立，馮成良，等.基于CFD-FASTRN的導彈折疊彈翼展開過程模擬［J］.彈箭與制導學報，2015，35（2）:5-8. LI Zhen，DONG Yu-li，FENG Cheng-liang，et al.Simulation of deployment of missile folded wings based on CFD-FASTRAN［J］.Journal of Projectiles，Rocekets，Missiles and Guidance，2015，35（2）:5-8.（in Chinese）

Dynamic Simulation and Experimental Study of Deployment Process of Missile Folding-wing

ZHEN Wen-qiang，JI Yong-qiang，SHI Yun-guo
（Institute of Systems Engineering，China Academy of Engineering Physics，Mianyang 621000，Sichuan，China）

The deployment process of transverse folding-wings of missiles is studied.The mathematical model and dynamic simulation model of deployment process of folding-wing in missile launching and ground tests are both established，in which the influences of friction and aerodynamic force are considered.The folding-wing were designed and manufactured.The images of deployment process of foldingwings are obtained using the high speed photography during ground test.The research results show that the test results are in good agreement with those of mathematic and dynamic simulation models.A value range of friction moment is also provided from the test results，which can support the design and application of folding-wing.

ordnance science and technology；folding-wing；deployment；dynamic simulation；experiment

TJ760.13

A

1000-1093（2016）08-1409-06

10.3969/j.issn.1000-1093.2016.08.010

2016-01-06

中國工程物理研究院總體工程研究所創新與發展基金項目（15CXJ13）

甄文強（1989—），男，工程師。E-mail:413zhenwq@caep.cn；姬永強（1977—），男，高級工程師。E-mail:jiyq@caep.cn