跨聲速運動對射彈阻力及空化特性的影響

黃闖，黨建軍，李代金，羅凱

（西北工業大學航海學院，陜西西安710072）

跨聲速運動對射彈阻力及空化特性的影響

黃闖，黨建軍，李代金，羅凱

（西北工業大學航海學院，陜西西安710072）

為研究在跨聲速運動過程中超空泡射彈的流體動力特性和流場的空化情況，基于流體體積分數多相流模型、Schnerr-Sauer空化模型、Realizablek-ε湍流模型、Tait液體狀態方程和運動框架模型構建了可壓縮超空化流場的數值模型，通過與文獻［11］試驗結果進行對比，完成模型驗證，采用數值方法模擬在馬赫數為0.202～1.281速度范圍內射彈的外流場。研究結果顯示：跨聲速運動過程中超空泡射彈的阻力系數與流場駐點的密度峰值有關，隨速度的升高而顯著增大；激波對彈體附近超空泡的形態和尺度有顯著的影響，亞聲速工況下超空泡尺寸與理論值接近并且受速度的影響很小，超聲速工況下超空泡的尺寸隨速度的增加而大幅度減小。研究結果對超空泡射彈的外形設計和彈道預報有參考價值。

兵器科學與技術；超空泡射彈；跨聲速運動；空化特性；液體狀態方程；激波

0 引言

超空泡射彈是一種通過火炮發射高速彈丸對水雷、魚雷和蛙人等水下目標實行硬殺傷的武器系統［1-2］。依托超空化減阻以及合理的流體動力外形和衡重特性設計維持彈道穩定，使得彈丸在水下無動力飛行超過100m后仍具有不低于300m/s的速度，剩余動能足以對水下目標造成致命毀傷［3-4］。提高發射速度是增大射彈的打擊范圍和提高毀傷能力的有效途徑，因此設計優良的超空泡射彈通常以水下超聲速發射，彈體入水后在阻力作用下將經歷由超聲速至亞聲速的跨聲速運動過程［5］。

射彈以聲速飛行時，在頭部駐點區域液體的壓縮率超過30%，流場發生劇烈的自然空化現象，并伴隨著激波。因此，射彈在跨聲速運動時流場的空化規律和彈體的流體動力特性與常規低速超空化流動有很大的不同［6-7］。Savchenko等［8］在重力式水洞中開展了50～150m/s的超空泡試驗，對空泡形態、空化器阻力特性等開展了研究。Vlasenko等［9］對亞聲速及接近聲速的超空泡射彈進行試驗，研究了高速超空化流場中彈體與空泡之間的相互作用，證明了液體可壓縮性對流場有顯著的影響。美國學者在紐波特海軍水下作戰中心成功開展了跨音速超空泡射彈試驗，并拍攝到了速度為1549m/s超空泡射彈在水中產生的弓形激波［10］。Hrubes等［11］通過高速攝影技術研究了超空泡射彈水中運動階段的空泡發展過程、彈體姿態以及弓形激波等。Kirschner等［12］通過試驗研究和數值模擬的方法闡述了水下超聲速流動的自然空化和激波等問題。從國內外公開發表的文獻來看，對于跨聲速超空泡射彈的研究還主要集中在水下激波的捕捉、超空泡形態以及彈道穩定性等方面，關于跨聲速運動過程中流場空化規律和彈體流體動力特性的相關研究鮮見報道。

本文基于商用計算流體力學（CFD）軟件，考慮液體可壓縮性和空化效應，結合流體體積分數（VOF）多相流模型和運動框架模型，針對超空泡射彈在跨聲速運動過程的外流場開展數值模擬研究，得出速度在300～1900m/s（馬赫數Ma為0.202～1.281）范圍內射彈的流體動力特性和流場的流動及空化規律，研究結果可為超聲速射彈優化設計和彈道預報提供參考。

1 數值模型和經驗公式

1.1數值模型

1.1.1數值模型的建立

超空化流動的控制方程包括氣體與液體（簡稱氣液）兩相流的連續方程、動量方程和湍流方程。根據文獻的研究結果［13］，本文研究的問題可采用VOF多相流模型進行模擬；空化現象可采用空化模型計算相間質量傳遞予以考慮；湍流控制方程可采用Realizablek-ε湍流模型，該模型穩健性好，適用于模擬復雜的流動；湍流模擬中近壁面處理方法可選用尺度化壁面函數。

模擬射彈的跨聲速運動，必須考慮液體的可壓縮性。Tait方程是通過采用非線性回歸的方法，對能夠反應壓力-速度-溫度三者關系的試驗數據進行擬合，而得到液體狀態方程［14］。為了簡化模型，建模過程中不考慮流場溫度變化對物性的影響，采用忽略溫度修正項的簡化Tait方程。簡化Tait液體狀態方程為

聲速是介質中微弱壓力擾動的傳播速度，計算方法為

式中:p0為參考壓力，取101325Pa；ρ0為參考壓力下的液體密度，取1000kg/m3；K0為參考壓力下的液體體積彈性模型，取2.2GPa；n為密度指數，取7.15；p為當前壓力（Pa）；ρ為當前壓力下的液體密度（kg/m3）；K為當前壓力下的液體體積彈性模量（Pa）；c為水中聲速，約1483m/s.

1.1.2模型的簡化及網格劃分

超空泡射彈的頭部是唯一穩定的沾濕區域，同時還是90%以上航行阻力的來源。在研究跨聲速流場的流動規律、流體動力特性和空化特性時，采用無附體超空泡射彈作為研究對象。無附體超空泡射彈的幾何特征如下:全長155mm，前錐段長70mm，最大直徑15mm，頭部空化器直徑3mm.

水下跨聲速運動涉及激波和超空化的問題，可以通過構建合理的計算域而弱化邊界對流場的影響。所有算例的計算域直徑取50倍彈體最大直徑，計算域長度取10倍彈長，其中進口距射彈頭部3.5倍彈長，出口距射彈尾部5.5倍彈長［15］。

本文所研究的超空泡射彈飛行工況的空化數在10-4量級，理論空泡全長可達40m以上，考慮到射彈的流體動力特性僅僅只與超空泡前155mm部分的形態相關，因此選用軸向尺度較小的計算域僅以射彈附近的空泡形態作為研究對象。

針對所建立的計算域，采用ICEM-CFD軟件的O-Block技術劃分結構化網格。在近壁面處添加邊界層，根據湍流模型對y+的要求對底層網格進行優化，期以獲得更精確的湍流模擬結果。在相變區域和兩相界面處劃分足夠精細的網格，以得到清晰穩定的空泡。采用網格自適應技術，在計算過程中依據壓力梯度和速度梯度對局部網格進行細化。

基于上述模型簡化原則及網格劃分策略，建立無附體超空泡射彈流場的三維幾何模型并劃分網格，網格單元總數為120萬，射彈外形及網格劃分情況如圖1所示。

圖1　射彈外形及網格劃分情況Fig.1 Shape of projectile and meshing

1.1.3邊界條件

采用運動框架模型模擬超空泡射彈的真實運動狀態，以流體作為運動參考系，通過給定壓力確定流場的進出口邊界條件。

計算域入口和出口壓力均設為111125Pa，即水深1m處的絕對壓力；計算域的外側設置為滑移壁面，忽略剪切力以弱化計算域邊界對流場的影響；采用Schnerr-Sauer自然空化模型描述氣液兩相間的質量傳遞，模擬超空泡的生成和發展。計算域構建及邊界條件的設置如圖2所示。

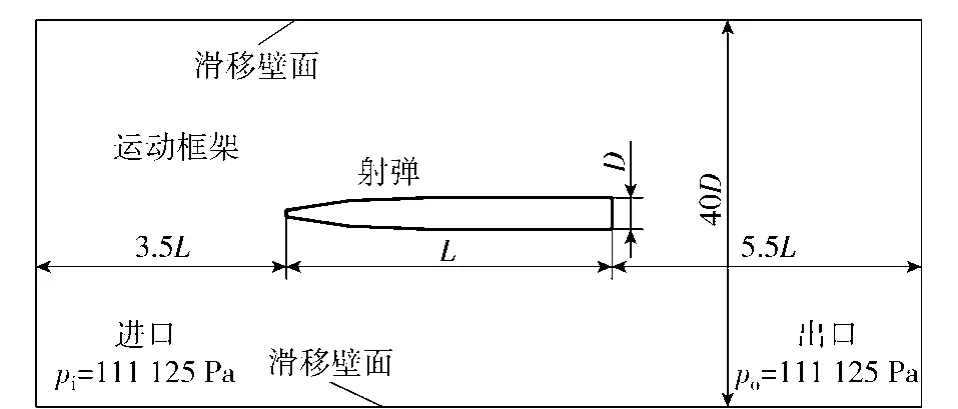
圖2　計算域構建及邊界條件設置Fig.2 Establishment of computational domain and setting of boundary conditions

受限于當前的發射技術，具有工程實踐意義的超空泡射彈最大入水僅略高于水中聲速。射彈作為動能武器，為保證毀傷能力水彈道末端速度不得低于300m/s.因此本文研究在300～1900m/s的速度工況下彈體的流體動力特性和流場的空化情況。

1.2經驗公式

空泡截面獨立擴張原理認為，空泡的每一個截面相對于空化器中心運動軌跡都以相同的規律擴張，僅依賴于空化器通過所論截面時刻的速度、阻力以及遠場與泡內的壓力差等因素，與此前或此后空化器的運動狀態無關［16］。空泡截面獨立擴張原理最初由前蘇聯學者Logvinovich于20世紀60年代提出，并不斷得到驗證和完善，是當前預測超空泡形態和空化器流體動力特性的理論基礎。

烏克蘭學者Savechenko基于空泡截面獨立擴張原理，參考自由航行試驗數據提出了預測超空泡外形的經驗公式［17］。Savechenko公式有充分的試驗基礎，能夠在較大空化數范圍內準確描述超空泡的形態，廣泛應用于超空泡航行器的設計。

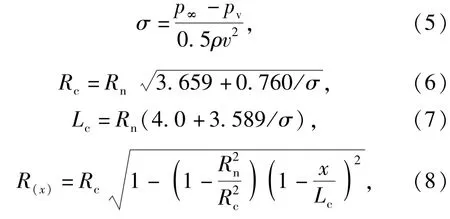
式中:σ為空化數；p∞為遠場壓力；pv為水飽和蒸氣壓力；Rn為空化器半徑；Rc為空泡最大截面半徑；Lc為空泡全長；x為空泡截面的軸向位置。

根據文獻［16］空化物體阻力特性的論述，在忽略液體可壓縮性的情況下，細長體在超空化流場中的阻力特性可采用（9）式計算:

式中:Cx為細長體在超空化流場中相對于迎流面積的阻力系數；Cx0為零空化數阻力系數，取0.827.

1.3模型驗證

基于提出的數值方法，采用可壓縮液體作為介質，將數值模擬結果與文獻［11］的試驗結果進行對比，驗證數值模型的合理性和置信度。

根據Hrubes等［11］的試驗結果，可以得到射彈飛行速度為970m/s（Ma=0.654）時空泡輪廓數據和射彈飛行速度為1530m/s（Ma=1.030）時流場中弓形激波的形態數據。

針對文獻［11］的射彈外形和運動參數，考慮液體可壓縮性對試驗過程進行數值模擬，并將計算結果與試驗數據進行對比。對于空泡輪廓和激波形態的數值模擬結果和試驗結果的對比分別如圖3和圖4所示。

圖3　超空泡輪廓的數值模擬與試驗結果對比Fig.3 Comparison of supercavitation outlines drawn by different methods

圖4　激波形態的數值模擬與試驗結果對比Fig.4 Comparison of shock waves drawn by different methods

如圖3顯示，對于文獻［11］所述的射彈，在970m/s速度工況下通過數值模擬所得超空泡輪廓與文獻提供的試驗數據基本吻合。

如圖4顯示，在1530m/s速度工況下，數值模擬所得流場密度等值線的分布規律與試驗拍攝得到的弓形激波一致。

綜上所述，在亞聲速工況和超聲速工況下，關于超空泡輪廓和弓形激波形態的數值計算結果與文獻［11］提供的試驗結果吻合，表明本文提出的考慮液體可壓縮性的數值方法是合理的。

2 數值模擬結果

基于所建模型，模擬超空泡射彈在水中以馬赫數為0.202～1.281的速度飛行時的流場，研究馬赫數對彈體的流體動力特性和流場的空化情況的影響規律，探索水下跨聲速運動對流場的影響機理。

2.1跨聲速運動過程流場的空化特性

根據數值模擬結果，統計各計算工況彈體附近的超空泡輪廓，不同工況空泡形態的對比結果如圖5所示，彈尾截面的空泡直徑與馬赫數的關系如圖6所示。

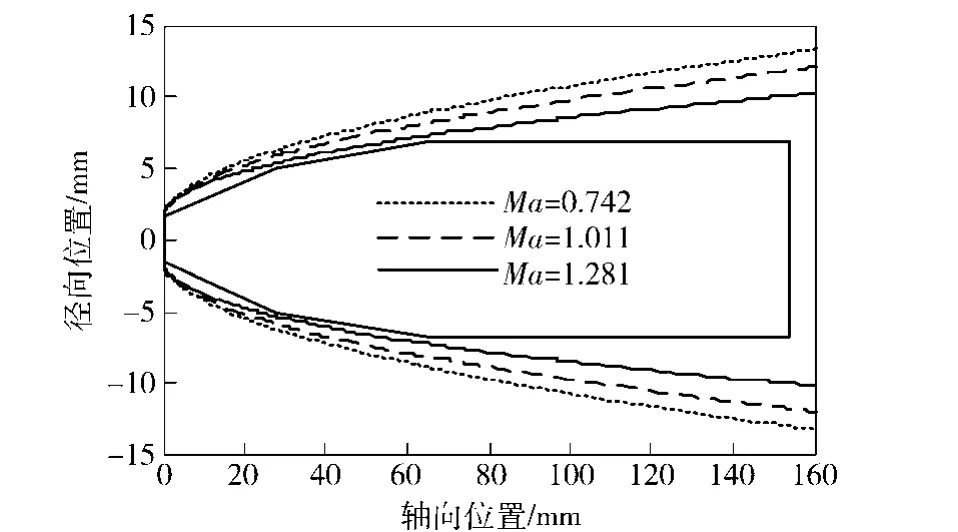
圖5　不同速度工況下超空泡形態的對比Fig.5 Shapes of supercavities under different working conditions

如圖5顯示:考慮液體可壓縮性時，在亞聲速、臨界聲速和超聲速3種工況下流場的空化情況有明顯的不同；隨著射彈飛行馬赫數的增加，彈體附近的空泡尺寸大幅減小。

如圖6顯示，射彈在馬赫數為0.202～1.281的速度范圍內，忽略液體可壓縮性的經驗公式描述的彈尾截面空泡直徑幾乎不受速度的影響。然而考慮液體可壓縮性的數值模擬結果則表明:在Ma＜0.8時，彈尾截面空泡直徑受飛行速度的影響不大，且與經驗公式計算結果一致；在Ma＞0.9時，彈尾截面空泡直徑隨射彈飛行速度的增加而大幅度減小；相對于小馬赫數工況，彈尾截面的空泡直徑在Ma=1.011時減小了10%，在Ma=1.146時減小了18%，在Ma=1.281時減小了30%.

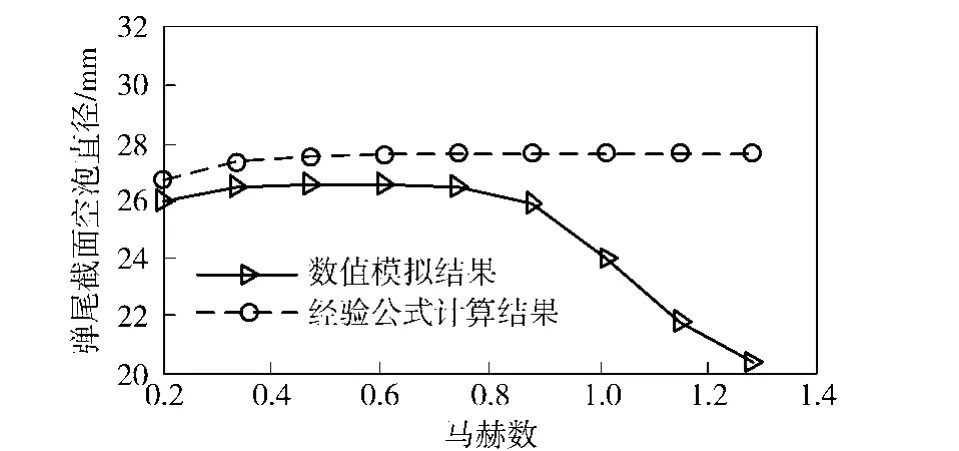
圖6　馬赫數對彈尾截面空泡直徑的影響Fig.6 Influence of Mach number on diameters of projectile' tail sections during transonic motion

2.2跨聲速運動中射彈的阻力特性

根據數值模擬結果，在馬赫數為0.202～1.281的速度范圍內，超空泡射彈的阻力系數與飛行速度的關系如圖7所示。

圖7　跨聲速運動過程中射彈的流體動力特性Fig.7 Hydrodynamic characteristics of projectiles' transonic motion

如圖7顯示:跨聲速運動過程中，射彈的阻力系數隨著馬赫數的增大而不斷增大，且跨越聲速前后二者關系并沒有明顯變化；較Ma=0.202的工況，Ma=1.281時射彈的阻力系數增大了23%；經驗公式計算所得的彈體阻力系數幾乎不受馬赫數的影響，不適用于描述高速工況下超空泡射彈的阻力特性；無附體超空泡射彈在彈體完全被空泡包裹的情況下，阻力幾乎全部來自于迎流面。

2.3跨聲速運動過程流場的流動規律

由2.1節和2.2節可知，射彈的飛行馬赫數對彈體的流體動力特性和流場的空化情況均有顯著的影響。對比分析射彈在亞聲速和超聲速工況下的壓力和密度的分布規律，以揭示射彈飛行馬赫數對外流場的影響機理。以6種不同馬赫數工況為例，流場縱剖面的等壓線分布規律對比結果如圖8所示。

圖8　不同馬赫數下射彈外流場的等壓線分布情況對比Fig.8 Isopiestic distribution of external flow field under different Mach numbers

如圖8顯示:Ma＜0.9時，為亞聲速流動狀態，高壓區位于射彈頭部駐點附近，并且壓力值和壓力梯度均按環形規律向四周逐漸衰減；Ma≈1時，為臨界聲速流動狀態，駐點壓力沿軸線迅速衰減，高壓區在沿來流方向被壓縮；Ma＞1時，為超聲速流動狀態，高壓區逐漸向后延伸并呈現弓形后掠特性，弓形區域頂端外側壓力梯度急劇增大，形成激波特性，并且激波的強度隨著馬赫數的增大而明顯增加。

結合圖5、圖6和圖7可以發現，射彈的飛行馬赫數對流場等壓線和彈尾截面空泡直徑的影響規律一致。因此認為:超空泡射彈以Ma＞1的速度飛行時，流場中形成激波并導致高壓區呈現弓形后掠特性，致使彈體附近的壓力分布改變并且壓力值增大，最終導致彈體附近的空泡尺度急劇減小；Ma＜1時，因為射彈的飛行速度對流場的壓力分布影響不大，空泡形態并未隨速度的增加而顯著變化。

射彈的飛行馬赫數分別為0.607和1.281時流場縱剖面的密度分布如圖9所示。

如圖9顯示:亞聲速工況下，流場的高密度區域主要分布在射彈頭部以前；超聲速工況下，流場的高密度區域向后延伸并呈現弓形分布規律，且弓形區域頂端外側密度梯度較大。

結合圖8和圖9，射彈在跨聲速飛行時流場的壓力和密度的分布規律相對應。根據文獻［11］，射彈的超聲速運動流場產生局部的大密度梯度區域，并且折光率發生變化，呈現出可以觀察到的弓形激波特性。圖8和圖9中捕捉得到壓力、密度的弓形分布規律可以表征超聲速射彈在水下形成的弓形脫體激波。超聲速工況下，在射彈的外流場中激波的出現將改變壓力、密度等流動參數的分布規律，并最終導致彈體附近空泡尺度急劇減小。

根據數值模擬結果，不同速度工況流場駐點的密度峰值隨速度的增加而單調增加，且在亞聲速和超聲速工況下二者關系并沒有明顯差異，與圖7中展示的阻力與馬赫數的關系相似。由此可以認為，在超空泡射彈的跨聲速運動過程中，速度的增大引起射彈駐點區域液體的密度增加，并最終導致射彈的迎流面阻力系數逐漸增大，激波對射彈的迎流面阻力系數沒有明顯影響。

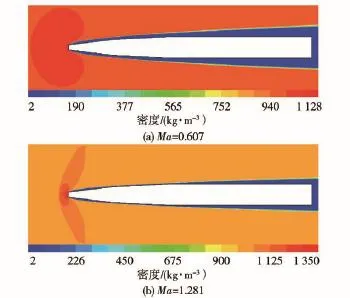
圖9　超聲速和亞聲速工況流場的密度分布Fig.9 The comparison of density distributions between subsonic flow field and supersonic flow field

3 結論

考慮液體的可壓縮性和流場的超空化現象，基于運動框架模型構建了無附體射彈的跨聲速超空化流場的數值模型。采用數值模擬的方法研究了在馬赫數為0.202～1.281的速度范圍內射彈的阻力特性和流場的空化情況。通過對比不同工況下流場的流動參數，揭示了射彈飛行速度對阻力和空化特性的影響機理。通過本文研究可以得出如下結論:

1）亞聲速狀態下，彈尾截面的空泡尺寸受射彈飛行速度的影響不大，且與經驗公式計算結果接近；接近和超越聲速狀態下，彈尾截面的空泡尺寸大幅度減小，且與經驗公式計算結果表現出很大的差異；較Ma=0.202工況，彈尾截面的空泡直徑在Ma= 1.011時減小了10%，在Ma=1.146時減小了18%，在Ma=1.281時減小了30%.

2）射彈在跨聲速運動過程中，考慮液體可壓縮性時彈體的阻力系數與流場駐點密度相關，且隨著速度的增大而增大；忽略液體可壓縮性的經驗公式計算所得的彈體阻力系數幾乎不受飛行速度的影響，不適用于預測超空泡射彈在跨聲速飛行過程的流體動力特性；射彈以Ma=1.281的速度飛行時，阻力系數較低速工況增大了23%；射彈亞聲速飛行時，液體可壓縮性的表現不明顯且對彈體阻力系數影響不大。

3）射彈超聲速飛行時，流場的壓力和密度的分布規律較亞聲速工況有很大差異:Ma＞1時流場的高壓區呈現后掠特性并形成弓形激波；激波的出現致使彈體附近的超空泡尺度急劇減小，對射彈的迎流面阻力特性卻沒有明顯的影響。

研究結果可為跨聲速超空泡射彈的外形優化和彈道預報工作提供參考。

（References）

［1］ 張志宏，孟慶昌，金永剛，等.超聲速細長錐型射彈超空泡流動數值計算方法［J］.華中科技大學學報:自然科學版，2014，42（1）:39-43. ZHANG Zhi-hong，MENG Qing-chang，JIN Yong-gang，et al. Numerical method of supercavitating flow past a slender cone type projectile traveling at supersonic speed［J］.Journal of Huazhong University of Science and Technology:Nature Science，2014，42（1）:39-43.（in Chinese）

［2］ 衛平，侯健，楊柯.超空泡射彈研究綜述［J］.艦船電子工程，2008，28（4）:13-17 WEI Ping，HOU Jian，YANG Ke.Summary of supercavitating projectile researches［J］.Ship Electronic Engineering，2008，28（4）:13-17.（in Chinese）

［3］ Saranjam B.Experimental and numerical investigation of an unsteady supercavitating moving body［J］.Ocean Engineering，2013，59（2）:9-14.

［4］ Shafaghat R，Hosseinalipour S M，Lashgari I，et al.Shape optimization of axisymmetric cavitators in supercavitating flows，using the NSGA II algorithm［J］.Applied Ocean Research，2011，33（3）:193-198.

［5］ Zhang P，Fu H.The numerical simulation of supercavi-tation around projectiles from subsonic to supersonic［J］.Journal of Pro- jectiles，Rockets，Missiles and Guidance，2009，29（5）:166-169.

［6］ Zheng J G，Khoo B C，Hu Z M.Simulation of wave-flow-cavitation interaction using a compressible homogenous flow method［J］. Communications in Computational Physics，2013，14（2）:328-354.

［7］ Liu J，Meng Q，Zhang Z，et al.Numerical simulation of compressible supercavitating flow［J］.Journal of Naval University of Engineering，2011，23（4）:48-52.

［8］ Savchenko Y N.Control of supercavitation flow and stability of supercavitating motion of bodies［C］∥VKI Special Course on Supercavitating Flows.Brussels，Belgium:RTO-AVT/VKI，2001.

［9］ Vlasenko Y D.Experimental investigation of supercavitation flow regimes at subsonic and transonic speeds［C］∥15th International Symposium on Cavitation.Osaka，Japan:CAV，2003:1-8.

［10］ Jenkins A，Evans T.Sea mine neutralization using the AN/AWS-2 rapid airborne mine clearance system［C］∥2004 IEEE Aerospace Conference Proceedings.Big Sky，MT:IEEE，2004:2999-3005.

［11］ Hrubes J D.High-speed imaging of supercavitating underwater projectiles［J］.Experiments in Fluids，2001，30（1）:57-64.

［12］ Kirschner I，Gieseke T，Kuklinski R.Supercavitation research and development［J］.Undersea Defense Technologies，2002，28（1）:46-58.

［13］ Yu K，Zhang G，Zhou J，et al.Numerical study of the pitching motions of supercavitating vehicles［J］.Journal of Hydrodynamics，2012，24（6）:951-958.

［14］ Lyons C G.A simple equation of state for dense fluids［J］.Journal of Molecular Liquids，1996，69:269-281.

［15］ 黃闖，羅凱，黨建軍，等.流域徑向尺度對自然超空泡的影響規律［J］.西北工業大學學報，2015，33（6）:936-941. HUANG Chuang，LUO Kai，DANG Jian-jun，et al.Influence of flow field's radial dimension on natural supercavity［J］.Journal of Northwestern Polytechnical University，2015，33（6）:936-941.（in Chinese）

［16］ Vasin A D.The principle of idependence of the cavity sections expansion（Logvinovich's principle）as the basis for investigation on cavitation flows［C］∥2001 RTO/AVT Lecture Series on Supercavitating Flows.Belgium:RTO，2001:1-27.

［17］ Savchenko Y N.Supercavitation—problems and perspectives［C］∥4th International Symposium on Cavitation.Passadenia，CA，US:California Institute of Technology，2001.

Influence of Transonic motion on Resistance and Cavitation Characteristics of Projectiles

HUANG Chuang，DANG Jian-jun，LI Dai-jin，LUO Kai
（School of Marine Science and Technology，Northwestern Polytechnical University，Xi'an 710072，Shaanxi，China）

In order to research the resistance characteristics and flow cavitation of supercavitation projectiles during transonic motion，a numerical model of a compressible and supercaitation flow field is established based on VOF multiphase model，Schnerr-Sauer cavitation model，realizable k-ε turbulence model，Tait liquid state equation and moving frame model.The proposed model is validated by comparing the numerical results with those in Ref.［11］，and the external flow field of supercavitation projectile flying at Mach number between 0.202 and 1.281 is simulated.The simulated results show that，during transonic motion，the resistance coefficient of projectile is related to the peak value of density at the stationary point of flow field and increases with the increase in flying speed；and the shockwaves have significant influence on the shapes and dimensions of supercavities near projectile.Under subsonic condition，the flying speed of projectile has no significant influence on the dimensions of supercavities，and the shapes of supercavities coincide with theoretical results；under supersonic condition，the dimensions of supercavi-ties decrease sharply with the increase in flying speed.

ordnance science and technology；supercavitation projectile；transonic motion；cavitation characteristic；state equation of liquid；shockwave

O351.2

A

1000-1093（2016）08-1482-07

10.3969/j.issn.1000-1093.2016.08.021

2015-12-24

國家自然科學基金項目（51579209、51409215）

黃闖（1989—），男，博士研究生。E-mail:hc_389@163.com；黨建軍（1965—），男，教授，博士生導師。E-mail:janjund@nwpu.edu.cn