雙重偽補Ockham代數的理想與濾子同余關系的注記

趙秀蘭，初元紅，史西專

（黃河科技學院數理部，河南，鄭州，450063）

雙重偽補Ockham代數的理想與濾子同余關系的注記

趙秀蘭，初元紅，史西專

（黃河科技學院數理部，河南，鄭州，450063）

依據雙重偽補Ockham代數的核理想和余核濾子判別定理以及具有核理想和余核濾子同余關系表達式，研究了雙重偽補Ockham代數的核理想和余核濾子同余關系的同余置換性，證明了雙重偽補Ockham代數核理想同余關系和余核濾子同余關系是同構的.

Ockham代數；偽補代數；雙重偽補Ockham代數；核理想；余核濾子；同構

0　引言

文獻[1]研究了雙重偽補Ockham代數，簡稱dpO代數，它是在有界分配格上賦予三個一元運算f,*,+的代數，屬于（2,2,1,1,1,0,1）類型的代數類，其中（L;∧,∨,f,0,1）∈O（符號O表示Ockham代數），（L;∧,∨,*，0，1）∈p（符號p表示偽補代數），（L;∧,∨,+，0,1）為對偶的偽補代數，且兩組一元運算f,*和f,+滿足交換律（p代數，pO代數，對偶p的代數的詳細信息見文獻[2-3]）.在序代數結構的研究中，借助理想和濾子，特別是核理想與余核濾子，是人們認識序代數-Ockham代數類的結構及同余關系的一個重要工具.文獻[4]研究了雙重偽補Ockham代數的理想和濾子，給出了雙重偽補Ockham代數具有核理想和余核濾子同余關系表達式以及核理想和余核濾子判別定理，證明了雙重偽補Ockham代數的核理想格與其余核濾子格同構.文獻[5-9]就相關Ockham代數類的理想與濾子做了研究.本文將在文獻[4]的基礎上，進一步討論雙重偽補Ockham代數核理想與余核濾子同余關系的性質.

1　基本知識

定義1.1[2-3]一個偽補代數（簡稱p-代數）是一個代數（L;∨,∧,*,0,1），它具有一個最小元0及一個映射*：L→L使得x*=max{y∈L|x∧y=0}.

定義1.2[2-3]一個對偶偽補代數是一個代數（L;∨,∧,+,0,1），它具有一個最大元1及一個映射+：L→L使得x+=min{y∈L|x∨y=1}.

定義1.3[2-3]設（L;∨,∧,0,1）是一個有界分配格，其上賦予一個一元運算f，若f滿足條件：

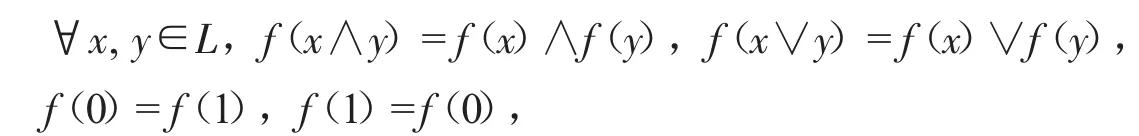
稱（L;∨,∧,f,0,1）是一個Ockham代數（簡記為O）.

定義1.4[10]設（L;∨,∧）是一個格，I是格L的子格，若x,y∈L，y≤x∈I總有y∈I，稱子格I是格L的理想.對偶地，F是格L的子格，若x,y∈L，y≥x∈F總有y∈F，稱子格F是格L的濾子.

定義1.5[1]設（L;∨,∧,0,1）是一個有界分配格，其上賦予三個一元運算f，*，和+，其中（L；f）是Ockham代數，（L；*）是偽補代數，（L；+）是對偶偽補代數，且三個一元運算滿足條件：

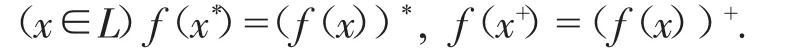
稱（L;∨,∧,f,*,+,0,1）是雙重偽補Ockham代數（簡稱dpO代數）.

定義1.6[1]設（L;∨,∧,f,*,+,0,1）是dpO代數，θ是L的一個格同余關系，若

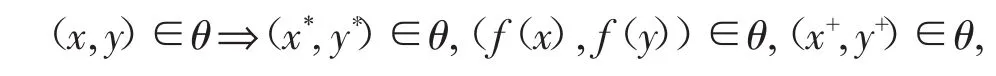
則稱θ是L的同余關系.符號ConL表示L的全體同余關系構成的集合.

定義1.7[4]設（L;∨,∧,f,*,+,0,1）是dpO代數，對于L的理想I，若存在L的一個同余關系φ，使得I=Kerφ，其中Kerφ={x∈L|x≡0（φ）}，稱理想I為L的核理想.

對于L的濾子F，若存在L的一個同余關系φ，使得F=Cokerφ，其中，

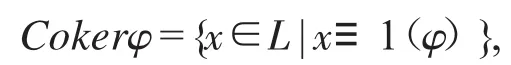
稱濾子F為L的余核濾子.

引理1.1[4]設（L;∨,∧,f,*,+,0,1）是dpO代數，則L上的一個理想I是核理想當且僅當（?a∈L）a∈I?{a*+,f（a*）}?I..

設L是dpO代數，符號I（L）和KI（L）分別表示L的全體理想和核理想構成的集合.

引理1.2[4]設L是dpO代數，則KI（L）是I（L）的子格.

引理1.3[4]設L是dpO代數，L的一個濾子F為余核濾子當且僅當

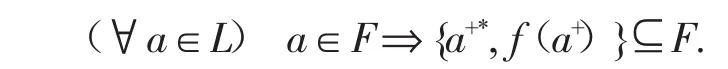
設L是dpO代數，符號F（L）和CokF（L）分別表示L的全體濾子和余核濾子構成的集合.

引理1.4[4]設L是dpO代數，CokF（L）是F（L）的子格.

引理1.5[4]設L是dpO代數，KI（L）≌CokF（L）.

沿用文獻[4]中的術語，設L是dpO代數，I是L上的核理想，F是L上的余濾子，分別定義L上的等價關系：

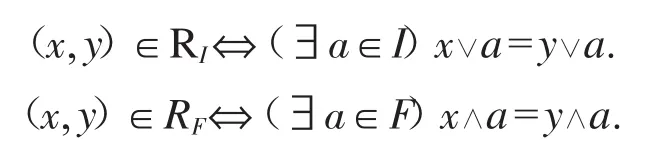
在文獻[4]中，已論證過RI∈ConL,RF∈ConL,且RI,RF分別是具有核理想I和余核濾子F的最小同余.雙重偽補Ockham代數的核理想格與其余核濾子格同構.那么，核理想同余關系與余核濾子同余關系能否構成一一對應，下面的定理2.4給出了答案.

2　主要結果

另一方面，設F1,F2∈CokF（L）,由文獻[4]得，F1=CokerRF1F2=CokerRF2.所以，若RF1≤RF2,CokerRF1≤CokerRF2，故RF1≤RF2.

設L是dpO代數，θ,φ∈ConL，定義L上的一個等價關系.

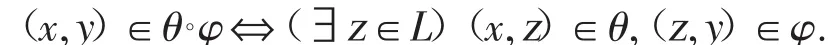
易見，θ°φ是L上的同余關系.

若θ,φ∈ConL，且θ,φ滿足關系式θ°φ=φ°θ，則稱同余關系θ,φ具有同余置換性.對于任意的I1,I2∈KI（L），F1,F2∈CokF（L），則RI1,RI2以及RF1,RF2具有同余置換性.定理2.2設（L;∨,∧,f,*,+,0,1）是dpO代數，I1,I2∈KI（L），F1,F2∈CokF（L），則

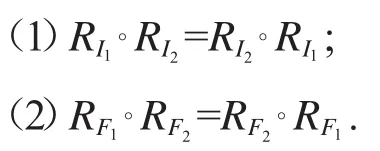
證明（1）令（x,y）∈RI1°RI2則存在z∈L，使得（x,z）∈RI1,（z,y）∈RI2.于是存在

i1∈I1,i2∈I2，使得

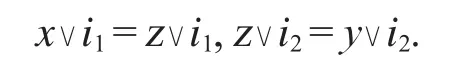
所以x∨i1∨i2=y∨i1∨i2

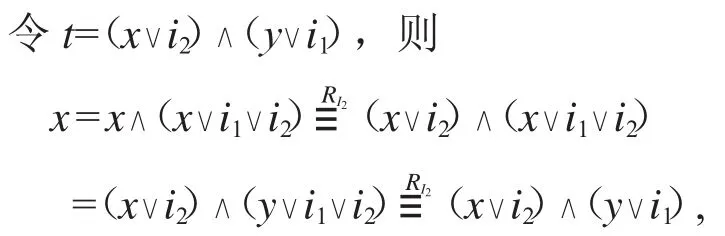
所以，（x,t）∈RI2.

又因

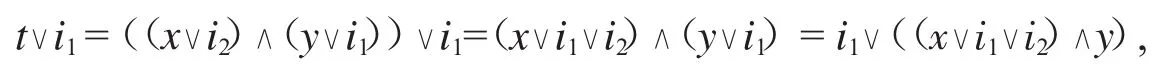
定理2.1設（L;∨,∧,f,*,+,0,1）是dpO代數，I,J∈KI（L），F1,F2∈CokF（L），則

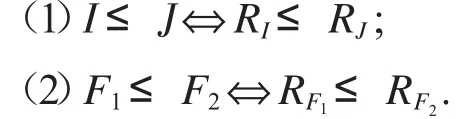
證明（1）設I,J∈KI（L），I≤J，由RI,RJ的定義知，RI≤RJ.

另一方面，設I,J∈KI（L），RI≤RJ，則KerRI≤KerRJ.由文獻[4]知，

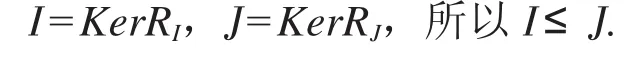
（2）設F1,F2∈CokF（L），由RF1,RF2的定義知，若F1≤F2,則RF1≤RF2.

所以t≡RI1（x∨i1∨i2）∧y=（y∨i1∨i2）∧y=y.

即t≡RI1

y.因此（x,y）∈RI2°RI1,從而得到RI1°RI2≤RI2°RI1.類似地，可得到相反的不等式，因此（1）成立.

（2）假設（x,y）∈RF1°RF2,則存在z∈L，使得（x,z）∈RF1,（z,y）∈RF2，則存在f1∈F1, f2∈F2，有

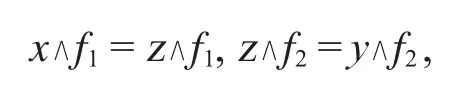
所以x∧f1∧f2=y∧f1∧f2.）.

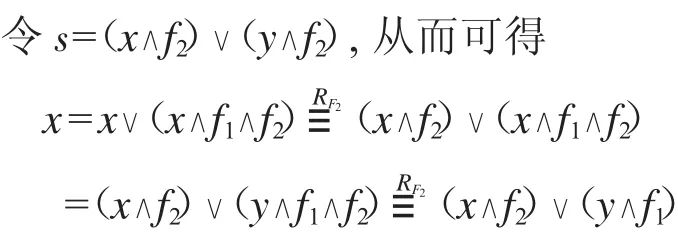
因此，（x,s）∈RF2.

又因

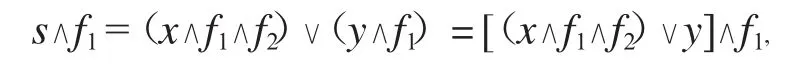
所以s≡RF1（x∧f1∧f2）∨y=（y∧f1∧f2）∨y=y.

即s≡RF1

y.所以（x,y）∈RF2°RF1,從而得到RF1°RF2≤RF2°RF1.類似地，可得到相反的不等式，因此（2）成立.

設L是dpO代數，對于L的每一個余核濾子F和核理想I，記集合，

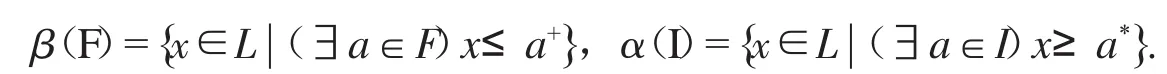
引理2.1[4]設（L;∧,∨,f,*,+,0,1）是dpO代數，又設I及F分別是L的核理想與余核濾子，則

（1）α（I）是L的余核濾子；

（2）β（F）是L的核理想.

根據RI，RF的定義，那么，余核濾子α（I）和核理想β（F）的同余關系將與核理想I與余核濾子F之間建立下列等式關系.

定理2.3（1）KerRα(I)=I;

（2）CokerRβ(F)=F.

證明（1）由引理2.1知，α（I）是L的余核濾子，結合余核濾子同余關系的定義知，（x,y）∈Rα(I)?（?i∈α（I））x∧i=y∧i.由α（I）的定義知，?a∈I,i≥a*.

設x∈KerRα(I),即（x,0）∈Rα(I),則存在i∈α（I）,x∧i=0∧i=0,故x≤i*≤a**.又因I是L的核理想，由引理1.1知，若a∈I,則a**∈I.所以x∈I,因此KerRα(I)≤I.

另一方面，設x∈I,由α（I）的定義知，x*∈α（I）.又因x∧x*=0∧x*=0,故（x,0）∈Rα(I),即x∈KerRα(I),所以I≤KerRα(I).因此KerRα(I)=I.

（2）由引理2.1知，β（F）是L的核理想，結合核理想同余關系的定義知，

（x,y）∈Rβ(F)?（?j∈β（F））x∨j=y∨j.由β（F）的定義知，?a∈F,j≤a+.

設x∈CokerRβ(F),即（x,1）∈Rβ(F),則存在j∈β（F）,x∨j=1∨j=1,故x≥j+≥a++.又因F是的L余核濾子，由引理1.1知，若a∈F,則a++∈F.于是x∈F,所以CokerRβ(F)≤F,

另一方面，令x∈F,由β（F）的定義知，x+∈β（F）.由于x∨x+=1∨x+=1,故（x,1）∈Rβ(F),則x∈CokerRβ(F),所以F≤CokerRβ(F).因此CokerRβ(F)=F.

設L是dpO代數，對于L的核理想集KI（L）和余核濾子集CokF（L），由引理1.5知，KI（L）≌CokF（L）.下面考慮核理想和余核濾子及其它們的同余關系之間的關系.設Conk（L）={RI|I∈KI（L）},ConF（L）={RF|F∈CokF（L）},則有下列定理.

定理2.4（1）KI（L）≌Conk（L）;

（2）CokF（L）=ConF（L）.

證明（1）先證I,J∈KI（L），有RI∧RJ=RI∧J.由引理1.2知，I∧J∈KI（L）.又因I∧J≤I,I∧J≤J，故由定理2.1知，RI∧J≤RI,RI∧J≤RJ，所以RI∧J≤RI∧RJ.

設（x，y）∈RI∧RJ，由文獻[10]知，（x，y）∈RI且（x，y）∈RJ，則存在i∈I,j∈J使得x∨i=y∨i,x∨j=y∨j.從而（x∨i）∧（x∨j）=（y∨i）∧（y∨j）.于是x∨（i∧j）=y∨（i∧j）.

又因i∧j∈I∧J，故（x，y）∈RI∧J，所以RI∧RJ≤RI∧J.因此RI∧RJ=RI∧J.再證對任意的I,J∈KI（L），有RI∨RJ=RI∨J.由引理1.2知，I∨J∈KI（L）.注意到I∨J≥I,I∨J≥J，由定理2.1知，RI∨J≥RI,RI∨J≥RJ,所以RI∨J≥RI∨RJ.設（x，y）∈RI∨J，則存在i∈I及i∈J使x∨i∨j=y∨i∨j從而有

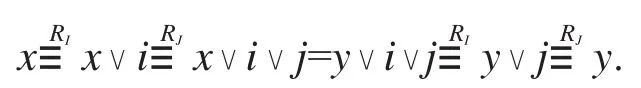
故

（x，y）∈RI∨RJ，所以有RI∨J≤RI∨RJ，因此RI∨RJ=RI∨J.

又因RI=RJ當且僅當I=KerRI=KerRJ=J,所以映射：I→RI建立起KI（L）→Conk（L）的一一對應，所以KI（L）≌ConF（L）.

（2）對偶地，可證CokF（L）≌ConF（L）.

由引理1.5和定理2.4可得到下列結論.

推論2.1KI（L）≌Conk（L）≌CokF（L）≌ConF（L）.

3　結論

本文在文獻[4]的基礎上，利用雙重偽補Ockham代數的核理想和余核濾子判別定理以及它們的同余關系表達式，論證了雙重偽補Ockham代數的核理想和余核濾子同余關系的同余置換性，獲得了雙重偽補Ockham代數核理想同余關系和余核濾子同余關系同構的結論.這一結論幫助我們了解雙重偽補Ockham代數的代數結構.

[1]FANG J.Ockham algebras with double pseudocomplementation[J].Algebra Universalis，2006（55）：277-292.

[2]BLYTH T S，VARLET J C.Ockham algebras[M].Oxford：Oxford University Press，1994.

[3]FANG J.Distributive lattices with unary operations[M].北京：科學出版社，2011.

[4]趙秀蘭，孫中舉.雙重偽補Ockham代數的理想與濾子[J].模糊系統與數學，2012，26（3）：70-76.

[5]方捷，吳麗云.擬補Ockham代數的理想與濾子[J].數學學報，2004，47（4）：647-652.

[6]趙秀蘭，方捷.平衡擬補Ockham代數的理想格[J].華南師范大學學報（自然科學版），2007（2）：42-47.

[7]方捷，沈嚇妹.平衡半偽補Ockham代數的濾子[J].模糊系統與數學，2010，24（3）：38-45.

[8]王雷波，方捷.雙重偽補代數的假值理想的一點注記[J].純粹數學與應用數學，2012，28（1）：119-122.

[9]王雷波，方捷.幾乎偽補格的核理想與W-理想[J].模糊系統與數學，2012，26（1）：61-66.

[10]GR?TZER G.Lattice theory[M].NewYork：W H Freeman and Company，1971.

A Note on the Ideal and Filter Congruence Relations on Double Pseudo-Complement Ockham Algebras

ZHAO Xiulan,CHU Yuanhong,SHI Xizhuan

（Department of Mathematics and Physics.HuangHe Science and TechnologyCollege, Zhengzhou 450063.Henan,China）

Byusingthe discriminant theoremofthe kernel ideals and co-kernel filters on a double Pseudo-complemented Ockham algebra,the expression ofthe kernel ideals and co-kernel filters congruence relations,the congruence permutation of kernel ideals and co-kernel filters are studied.It is shown that the kernel ideals congruence and the co-kernel filters congruence relations of double Pseudo-complemented Ockham algebras are isomorphic.

Ockham algebra;Pseudo-complemented algebra;double Pseudo-complement Ockham algebra;kernel ideal;co-kernel filter;isomorphism

51

A

1001-4217（2016）01-0035-06

2015-08-31

趙秀蘭（1982—），女，河南周口人，講師，碩士，研究方向：格論與序代數.E-mail：xiulanz@126.com.