激活經驗自然生成

蔣守成

【設計理念】

《解決問題的策略：轉化》雖然是蘇教版五下第七單元安排的內容，但學生在之前的學習過程中很早就有應用。例如：一年級計算9+6，想的是10+5，把一位數的進位加法轉化成10加幾；二年級估算504-198，想的是500-200，把三位數減法轉化成整百數的減法；五年級推導平行四邊形的面積公式時，把平行四邊形轉化成長方形；等等。

在我看來，本課與其說是學習轉化策略，不如說是學生進一步體驗、感悟過去學習中形成的認識和經驗，并逐步生成轉化策略。但我們僅僅依賴已有的轉化經驗，還不足以促成策略的自然生成。因為原有的經驗是零散的、模糊的、依附于特定情境的，需要使其清晰化、條理化，使之有利于策略的生成。因此，在教學時，應從學生已有的經驗出發，激活他們的經驗，讓他們先感悟轉化價值，也就是明晰為什么要轉化，使其產生學習策略的需求。

轉化作為解決問題的一種策略，通俗地講，就是把一個數學問題變成一類已經解決或比較容易解決的問題，從而使原問題得以解決的一種策略。在具體實施過程中，需要其他更加具體的、具有操作性的方法來配合實施。就學生解決問題來說，如果沒有轉化意識，一般不會主動考慮把問題由繁向簡、由難向易轉化；如果有轉化的愿望，但找不到轉化的具體方向，拿不出實施轉化的具體方法，仍然不會應用轉化策略。也就是說，要讓學生掌握能夠支持轉化策略有效實施的方法，運用已有的知識和經驗實現轉化，這是本課要達成的目標。主要體現在三個方面：（1）轉化的方向——化復雜為簡單，化未知為已知；（2）轉化的前提——等值轉化；（3）轉化的方法——變形、數形結合等。

基于上述思考，我對教材內容進行了重構，將回顧解決問題的過程前置到課前進行，讓學生自我回顧、自我整理，同時幫助學生提取已有的經驗，使他們對已經學過的轉化策略形成結構化的認識，為新的學習服務。課堂上，引導學生獨立思考、自主探究、踴躍展示，在整體構建的基礎上，依靠學生的經歷、體悟，讓學習變得更豐滿，讓策略自然生成。

【教學目標】

1.使學生初步學會運用轉化的策略分析問題，并能根據問題的特點確定具體的轉化方法，從而有效地解決問題。

2.使學生在反思中感受解決問題的特點和價值，進一步培養思維的條理性和嚴密性。

3.使學生進一步積累解決問題的經驗，增強解決問題的意識，主動克服在解決問題中遇到的困難，獲得成功的體驗。

【教學活動及意圖】

一、在故事中引入轉化

1.白發老人對青年人說了什么？

在內蒙古，有一對兄弟都是剽悍的騎士。他們常常打賭看誰的馬跑得快，結果是各有勝負，時間長了，他們也覺得乏味了。于是，哥哥提議：“我們來比一比誰的馬后跑到終點吧。”“好啊，比誰的馬跑得慢！”弟弟爽快地答應了。聽說有這種奇異的比賽，來了不少觀眾！比賽開始，觀眾們一起吶喊著：“加油！加油！加油！……”可是兄弟倆騎著馬都一動不動。時間一分一秒地過去，兩匹馬還是一動不動……“這樣比要比到何年何月？”觀眾們議論紛紛，哄笑起來。“怎么回事呀？”這時，來了一位滿頭白發的老人問道。有人告訴了他事情的經過。“原來這樣！”老人說，“你們看我的，我只要和他們悄悄說一句話，他們就會火燒屁股似地飛奔起來。”大家將信將疑地看著老人走到兄弟倆面前，不知他對兄弟倆說了什么，不到半分鐘，他們就騎著馬在草原上拼命奔跑起來……當然，比賽的規則不變：誰的馬后到終點，誰就是勝者。

猜一猜，老人對他們說了什么？（兄弟倆換馬騎）

2.追問故事中的轉化策略。

學生思考：（1）老人將比馬跑得慢轉化成了比什么？（2）為什么要轉化成比跑得快？（將比慢轉化成比快，使比賽更精彩、更好看）

師：這種轉化的策略對我們的數學學習又有什么啟發呢？今天，我們就一起來思考怎樣用轉化的策略解決數學問題。（板書課題）

【通過有趣的故事引入，激發學生學習的熱情，學生在運用轉化的策略解決“比誰的馬跑得慢”的問題的過程中，感受到轉化策略在生活應用中的價值，由此引導學生思考在數學學習中有沒有運用過轉化策略，以及怎樣運用轉化策略。】

二、在回顧中激活轉化

1.回顧以往轉化的經驗。

轉化作為一種常用而且非常有用的策略，我們對它并不陌生，在我們以前的學習中，已經多次運用過，想一想，在哪些地方用到了這種策略？（課前教師已經請學生自己做了整理）請在小組里交流交流。

學生展示交流：（1）面積公式的推導過程中用過“形”的轉化（平行四邊形→長方形，三角形、梯形→平行四邊形，圓→長方形）。（2）計算中用過“數”的轉化（異分母分數加減法→同分母分數加減法，小數乘除法→整數乘除法）。

2.初步感受“轉化”的價值。

進一步思考：求平行四邊形面積公式時為什么要轉化成長方形？異分母分數加減法計算為什么要轉化成同分母分數？如果不轉化成長方形和同分母分數行不行？

學生交流：轉化成我們學過的長方形和同分母分數比較簡單、方便。如果不轉化長方形和同分母分數，可以是可以，但比較復雜，平行四邊形可以數方格，異分母分數加減法可以轉化成已經學過的小數進行計算。

小結：無論是在“圖形與幾何”領域，還是在“數與代數”領域，我們通常運用轉化策略來解決問題，那么，在什么情況下需要轉化呢？轉化時往什么方向去轉化？可以用什么方法使轉化得以實現？帶著這些問題，我們來研究下面兩個圖形。

【這一板塊用了兩個前置，一是將回顧整理時間前置到課前，在課前用自主學習單的形式讓學生獨立回顧、整理，不僅能有效引領學生自我梳理，使他們形成個體基本的觀點，而且能適度呈現學生個體的學習差異，有利于課堂上集中學習時的提升和超越。二是將教材中回顧反思這一板塊前置到教學伊始，幫助學生激活已有的運用轉化策略解決問題的經驗，使之有利于后續策略的生成。】

三、在學習中進一步體悟轉化

1.問題引領：下面兩個圖形，哪個面積大一些？

操作要求：

（1）看一看，想一想：可以怎樣比較這兩個圖形的面積？

（2）試一試，做一做：把你的想法記錄在作業紙上。

（3）比一比，說一說：和你的小伙伴分享一下，你是怎樣比較這兩個圖形的面積的？

2.學生嘗試操作，教師走近學生了解情況，搜集資源。

3.呈現資源，分層交流。

第一層次：出示資源1（如圖1），交流數方格法。

談話：你能看出1號同學是怎樣比較這兩個圖形的面積的嗎？我們請他來介紹一下好嗎？

預設：學生匯報展示，我是用數格子的方法進行比較的，滿格的記作1，不滿格的記作0.5，加起來就可以比較了。

第二層次：出示資源2（如圖2），交流轉化法。

談話：能看懂別人的想法是非常了不起的！你能看懂他是怎么比較這兩個圖形的面積的嗎？

預設：學生邊比劃邊說，他通過平移和旋轉把兩個圖形轉化成了相同的長方形。（課件動態演示）

（面對提供資源2的學生）他說得對嗎？你是怎么想到先轉化再比較大小的，為什么不直接比較大小呢？（面對全體學生）這個方法好嗎？

第三層次：同步呈現資源1和資源2，比較兩種方法。

提問：這兩種不同的方法都比較出了兩個圖形的面積，你更欣賞哪位同學的？請說出你的理由。

交流：我更欣賞第2位同學的，他通過平移和旋轉把不規則圖形轉化成了規則圖形，這種方法更簡便。

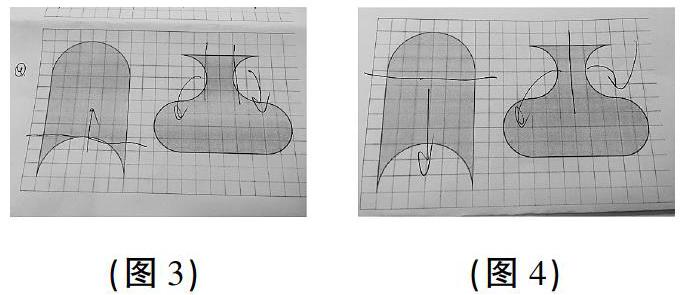
第四層次：同步呈現資源3（如圖3）和資源4（如圖4），解讀個性化的轉化方法。

談話：你能看出這兩位同學是怎樣比較的嗎？和同桌交流一下。

追問：這兩位同學的方法和剛才第2位同學的方法有什么共同之處嗎？

學生匯報交流，同時動態演示：都利用平移或旋轉把兩個不規則圖形轉化成了規則圖形，比較起來更方便。

小結：把不規則圖形通過平移、旋轉等方式轉化成規則的、簡單的圖形后，就可以直接比較出它們的大小了。（板書：復雜→簡單 不規則→規則）

【英國教育家斯賓塞說：“應該引導兒童自己進行探討，自己去推論，給他們講的應該盡量少些，而引導他們去發現的應該盡量多些。”因此，這一板塊分四個層次進行展示交流，在展示、交流和比較的過程中喚醒學生原有認知中的轉化體驗，讓學生自主經歷高水平的思考過程，讓他們學習的過程更豐滿。】

四、在練習中深入地體驗轉化

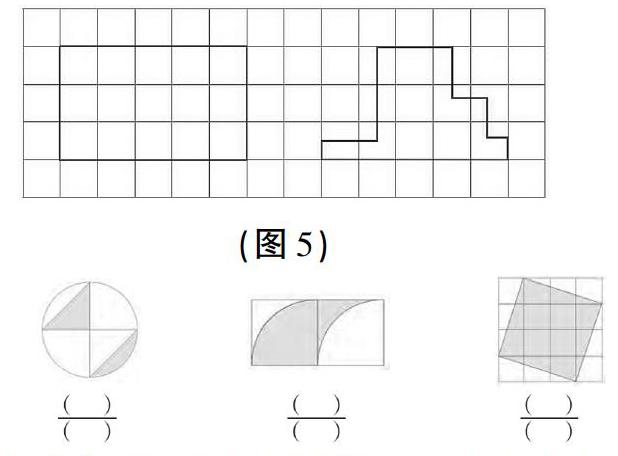
1.這樣兩個圖形（出示圖5），你能一眼看出哪個圖形的周長長一些嗎？請大家在作業紙上自己移一移、畫一畫，再比一比。

學生獨立解決后交流匯報。（通過平移轉化為相同的圖形，從而比較出它們的周長是相等的）

提問：如果要比較它們的面積，你打算怎么辦？（通過重疊直接比較）

小結：同樣是兩個圖形，我們發現，比較它們周長的時候，需要運用轉化的策略；比較它們面積的時候，通過重疊就能直接比較出大小。所以，我們在解決問題時首先要確定需不需要轉化，而后思考如何轉化。

2.用分數表示圖中的涂色部分。

提出要求：先獨立看圖填空，再交流你是怎樣想到轉化的方法的，以及分別是怎樣轉化的。

預設：對第3題有不同意見，讓學生展示自己的轉化方法，如分割平移、分割旋轉、數空白格子等，并驗證自己的結論。

【策略教學的目標不是解決某一個具體的問題，而是讓學生在解決問題的過程中體驗策略的形成過程，從而能靈活、創造性地使用策略解決問題。因此，本環節選擇教材中的兩個典型問題，進一步加深學生對圖形轉化的體驗，利用學習過程中生成的問題，進一步引導學生面對問題時要明晰為什么要轉化，以及如何利用已有的知識和經驗進行轉化。】

五、在問題解決中自覺地應用轉化

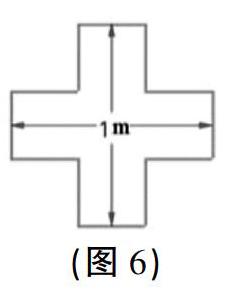
1.做標志。廣告公司準備做一批標志，做這樣一個標志的框架（如圖6）需要多少米材料？

（1）你準備怎么解決？獨立解決后與同桌說說你的思考過程。

（2）如果這個標志是一個實心的面，可以求出這個標志的面積嗎？

2.巧計算。9999+999+99+9可以轉化成怎樣的算式來計算？先想一想，再計算出結果。

【轉化策略在實際生活中應用得非常廣泛，但轉化的手段和具體方法是多樣而靈活的，既與實際問題的內容和特點有關，也與學生的認知結構有關。因此，在實踐應用環節，呈現適合學生探究的生活問題——做標志，鮮活的素材調動了學生學習的積極性，激活了學生的思維需要。同時，呈現計算問題，使學生體驗到運用轉化策略可以使計算更簡便，豐富學生對轉化策略的認知】

六、在反思中拓展轉化

這節課，我們學習了運用轉化的策略來解決問題，說一說你的收獲和體會。

轉化是我們解決數學問題時很重要的一種常用策略，在“數”中出現，也在“形”中出現，華羅庚爺爺說得好：數形結合百般好，隔離分家萬事休。你想知道數形結合好在哪兒嗎？下節課我們繼續來研究！

【讓學生對運用轉化策略解決問題的價值進行再認識，更加深刻地體會轉化的方向、前提、方法等。同時，從方法層面進行問題延展，延展到下節課的內容，目標是從最接近學生的起點走向更遠的終點。】

（作者系江蘇省常州市金壇區朝陽小學校長，江蘇省數學特級教師）