Math 3D在中職院校立體幾何教學中的實踐探究

【摘 要】分析國內(nèi)目前使用的幾種立體幾何教學軟件，介紹Math 3D軟件的基本功能與特點，利用教學實例講解Math 3D在立方體幾何教學中的具體應用，并針對Math 3D如何更好地實踐于中職院校提出了一些建議。

【關鍵詞】Math 3D 立體幾何 實踐探究

【中圖分類號】G 【文獻標識碼】A

【文章編號】0450-9889（2016）08B-0150-03

當前多媒體教學研究的目標人群大多集中在普通高中、高等院校，針對中職學生的特定研究較少。Math 3D是一款優(yōu)秀的立體幾何數(shù)學實驗與課件制作工具，其易懂易學，實用可靠，功能較多，適于中職院校學生的教學工作。它不僅能喚起學生的學習興趣，而且有利于培養(yǎng)學生的空間想象能力和自主學習能力。

一、中職院校學生的學情分析

當前，學生入讀中職學校，大多是未能進入高中，退而求其次做出的選擇，他們大多基礎知識薄弱，缺乏學習毅力、自覺性及自制力等良好學習習慣。雖然他們也曾信誓旦旦，但常常遇難而退，對老師、家長容易產(chǎn)生逆反心理。中職院校學生教育目標不同于高中教育，也有異于普通高等教育，中職教育的培養(yǎng)目標是“技能實用型”人才。

因此，中職立體幾何教學不宜過分強調(diào)思維的嚴謹性和邏輯的嚴密性，應正視學生基礎薄弱等實情，在學生現(xiàn)有水平的基礎上，突出其在專業(yè)課程和實際生活中的應用性，以及解決問題的自主性。

二、國內(nèi)目前使用的幾種立體幾何教學軟件

空間想象能力的培養(yǎng)，是培養(yǎng)學生學好立體幾何必須要過好的一關，何志光通過對調(diào)查問卷結果進行研究后認為，學生學習立體幾何感到困難的主要原因是空間想象能力和邏輯推理能力欠缺。當前教師針對學生空間識圖、空間想象力培養(yǎng)方面的教學工具一般有實物模型、折紙、掛圖等，這些工具在教學中均缺乏靈活性，因此隨之出現(xiàn)了各種教學軟件，如Cabri 3D，math 3.0，幾何畫板，超級畫板，flash，AutoCAD，Microsoft Office Word等。

其中，Cabri 3D是2004年法國推出的世界上第一款針對立體幾何教學的軟件，學生能夠利用其觀察和操控各種三維空間圖形，創(chuàng)建從簡單到復雜的各種動態(tài)幾何結構，但其不適用于中職學生自主學習的多方面要求。Math 3.0這款軟件的設計思想是面向功能性應用，不能滿足教師教學活動和學生學習過程中的多方面需求。幾何畫板，是美國知名的一款動態(tài)幾何軟件，其基本功能是動態(tài)幾何圖形的制作和變換，能夠動態(tài)地展現(xiàn)數(shù)和形的變化，但包含較多的操作技巧，入門與提高都要花費更多的時間和精力。超級畫板，是國內(nèi)具有自主知識產(chǎn)權的一款優(yōu)秀軟件，不僅能夠滿足中學數(shù)學教學和數(shù)學實驗的需求，而且操作方式簡便，體現(xiàn)了人性化、智能化、可視化、動態(tài)化和程序化，具有“寫、畫、測、變、編、演、推、算”八大功能，但針對立體幾何的教、學等功能不夠全面。對Flash，AutoCAD和Microsoft Office Word來說，F(xiàn)lash和AutoCAD制作過程需要較多的操作技巧，Microsoft Office Word僅能制作一些簡單的空間幾何體，這三款軟件均不適合學生自主學習和教學的多功能需求。

三、Math 3D的基本功能與特點

Math 3D軟件開發(fā)于2001年，是一個專業(yè)的數(shù)學實驗與課件制作工具，在易用性、動畫、三維圖像等方面具有良好的交互性，適于中職院校立體幾何的教學活動。

（一）三維圖像繪制

可在畫板中任意繪制空間幾何圖像，并動態(tài)保持幾何關系，可任意角度旋轉、縮放，達到激發(fā)學生學習興趣，培養(yǎng)學生的識圖能力、空間思維能力的目的。

（二）易用性

依據(jù)國人使用習慣設計，符合數(shù)學思維方法，采用向?qū)皆O計，一般教師10分鐘即可學會使用。學生經(jīng)過簡單教授后，亦能很快掌握。具有良好的交互性，在教學中可邊畫邊用，解決了課堂畫圖費時費力、空間感差的難題。

（三）動畫展示

可展現(xiàn)平移動畫、旋轉動畫、軌跡動畫、旋轉體動畫及顏色動畫等，以上動畫可獨立使用，也可以組合使用，是探索數(shù)學奧秘的理想工具。

（四）函數(shù)功能

支持直接輸入函數(shù)解析式，可繪制直角坐標方程、極坐標方程、參數(shù)方程等圖形，可通過旋轉構建空間曲面。可計算任意曲線之間的交點坐標，生成軌跡動畫。函數(shù)解析式中可使用動態(tài)參數(shù)，實現(xiàn)探究函數(shù)規(guī)律的目的。

此外提供了對圖像中動態(tài)數(shù)據(jù)測量（如線段的長度、角度、圓的面積等）的功能，經(jīng)過啟發(fā)式教學和學生實驗，學生正確理解概念、定理等變得直觀易懂。

四、教學實踐

建構主義教育理論的先驅(qū)皮亞杰認為，學習是同化與順應之間達到平衡之后的建構過程，知識是個體在與外界環(huán)境交互作用的過程中逐漸建構的結果。當今建構主義學習觀認為，學習是個體主動建構內(nèi)部心理表征的雙向建構過程；教學觀認為，數(shù)學教學是數(shù)學認知結構的教學，教師要以學生的數(shù)學認知結構特點及其變化規(guī)律為依據(jù)，確定其最近發(fā)展區(qū)，對數(shù)學教學過程進行精心設計、組織、協(xié)調(diào)、監(jiān)控和評價，以確保意義建構目標的實現(xiàn)。

通過了解學生對原有知識及結構的掌握程度等情況，可確定最近發(fā)展區(qū)，由此指導教學課件的創(chuàng)設。不斷重置教學內(nèi)容的深度、難度及最近發(fā)展區(qū)，如此循序漸進，引導學生不斷突破障礙，逐步跨上新臺階，學生易于養(yǎng)成良好的自主學習習慣。

下面以幾個實例來進行講解。

例1 識圖：棱臺與棱錐間的關系，見圖1。與三棱錐底面保持動態(tài)平行的平面（藍色）在移動過程中，學生感受棱錐與相應棱臺間的關系。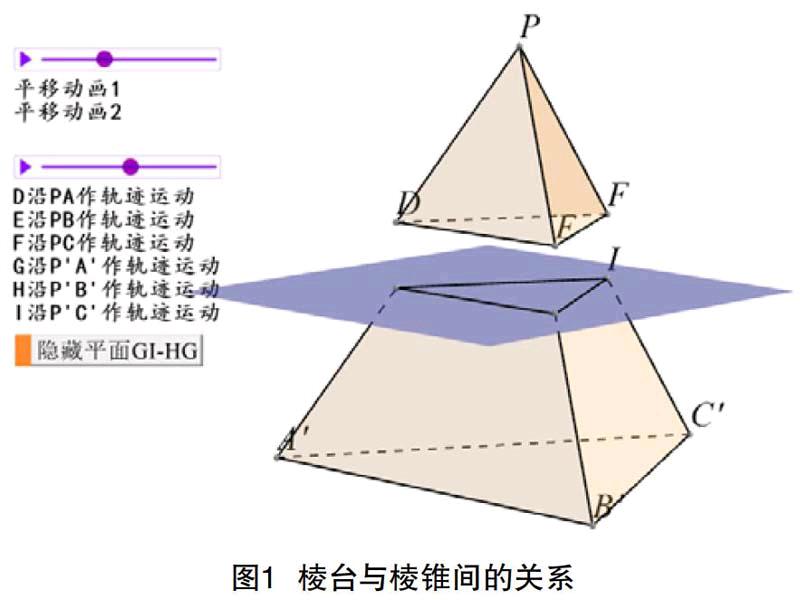

例2 圖2是空間內(nèi)的兩個相交的平面，根據(jù)要求將被遮擋部分改為虛線：（1）線AB沒有被平面α遮擋；（2）線AB被平面α遮擋。

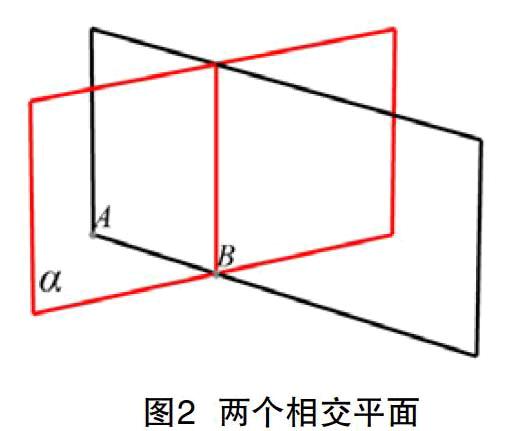
用Math 3D制作教學課件過程如下：

（1）在畫板中畫垂直于平面xOy且不重合的兩個平面AA'C'C與平面DD'E'E，交線BB'與 z 軸平行，分別標記顏色，記平面AA'C'C為α。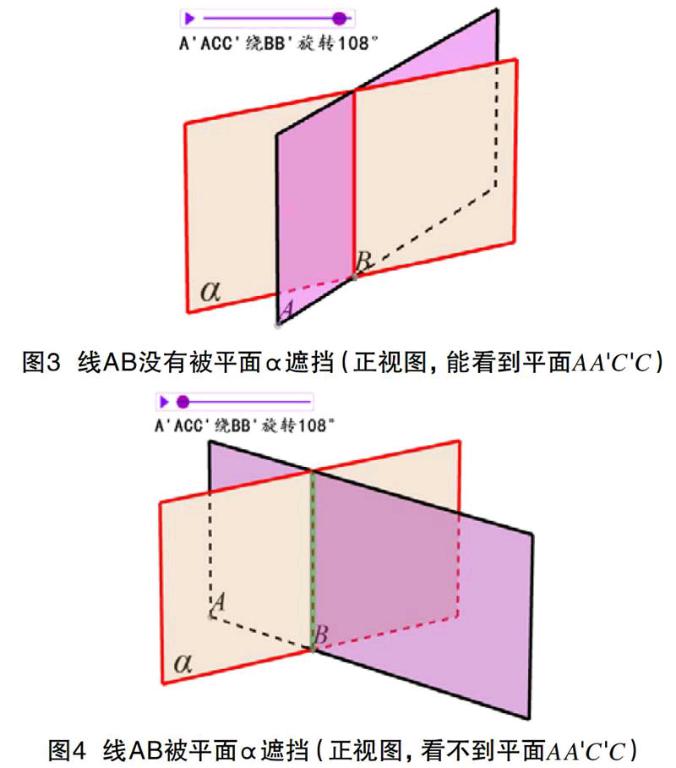

（2）點擊“動畫”工具菜單的“旋轉體動畫”功能，以BB'為旋轉軸，平面AA'C'C為旋轉對象，旋轉角度為108°，“隱藏”除點A、B外的其他點。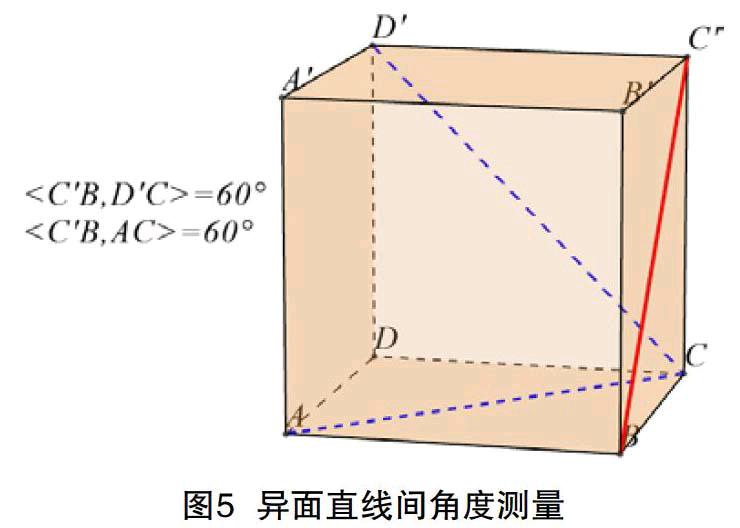

（3）右擊“動畫控制器”，動畫模式為“往復運動”，運動時長為“6秒”。

激活動畫，由此可清晰、直觀的識別兩個平面相互遮擋時各線段的顯隱問題，見圖3、4。

例3 正方體中直線BC'與AC、CD'互為異面直線（見圖5），經(jīng)證明可得異面直線BC'與AC、BC'與CD'之間的夾角均為60°；使用“變量”菜單中的“角度”功能，亦測得異面直線BC'與AC、BC'與CD'之間的夾角均為60°。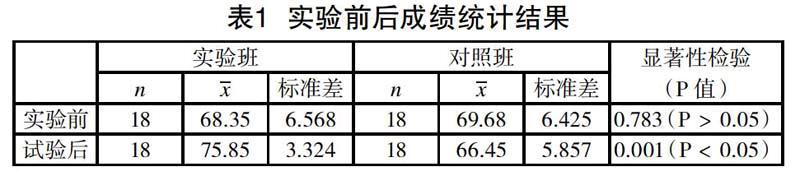

作者在確定中等學習程度學生的最近發(fā)展區(qū)后，用Math 3D課件進行教學，學生能夠認真聽講并進行良好互動。此外，在兩個班級中分別選取18名中等學習程度且大致相同的學生，實驗班用Math 3D教學，對照班用傳統(tǒng)教學，兩個月后進行小測。結果顯示，實驗班學生得分較對照班高，且差異顯著，見表1。

五、建議

Math 3D作為一款易用且功能強大的教學實驗工具，教師要鼓勵學生自主參與課件的制作，多與學生互動交流經(jīng)驗體會。教師要切實樹立并踐行終身學習理念，不斷探索Math 3D與其他教學工具及講授方法，融合“混合交互學習”法，做好學生的“引導者”。利用Math 3D設計制作教學課件時，教師要尊重各種成績層次的學生，嚴慈相濟，確定學生“最近發(fā)展區(qū)”后實施分層教學，以免扼殺學生的學習興趣。

【參考文獻】

[1]何志光.高中生學習立體幾何的障礙分析及教學研究[D].云南師范大學碩士學位論文，2007

[2]孫鳳丹，吳華.CABRI 3D環(huán)境下圓錐曲線的認知過程設計[J].中國教育技術裝備，2014（14）

[3]張景中，彭翕成.三款數(shù)學教育軟件的比較與設計思想分析[J].中國電化教育，2010（1）

[4]章建躍.建構主義對數(shù)學教育的啟示[J].數(shù)學通報，1998（4）

[5]徐梅丹，孟召坤，張一春.基于微信公眾平臺的混合設計與分析——以中職《AutoCAD制圖》課程為例[J].職業(yè)技術教育，2015（36）

【作者簡介】蘭偉興（1984— ），男，漢族，河北無極縣人，碩士研究生，現(xiàn)任教于廣西動力技工學校。研究方向：中職數(shù)學及教學研究。

（責編 盧建龍）