側窗探測動能攔截器末段軌控方案

王　洋，周　軍，趙　斌，尤雨驊

(1.西北工業大學 精確制導與控制研究所，西安　710072；2.中國運載火箭技術研究院，北京　100076)

?

側窗探測動能攔截器末段軌控方案

王洋1，周軍1，趙斌1，尤雨驊2

(1.西北工業大學 精確制導與控制研究所，西安710072；2.中國運載火箭技術研究院，北京100076)

針對側窗探測動能攔截器(SWDKKV)的末段軌控問題，基于變結構控制理論提出了一種新的軌控方案。首先考慮側窗約束，建立了三維空間下的軌控模型。隨后，針對側窗探測動能攔截器只能輸出定常開關推力及具有姿態定向約束的特點，提出了一種新型變結構滑模面，基于所提出的滑模面設計了適合于末段攔截的bang-bang形式的軌控方案，采用Lyapunov穩定性理論嚴格證明了所提出方案的穩定性。為了降低噴氣消耗，設計了滑模死區，且研究了能夠保證命中精度的滑模死區的參數取值范圍。仿真結果表明，所設計的軌控方案可確保動能攔截器直接撞擊目標，設置滑模死區可以在保證命中精度的同時降低噴氣消耗。

側窗探測；動能攔截器；末制導；軌控方案；滑模控制；滑模死區

0　引言

20世紀80年代以來，彈道導彈防御從核時代轉向非核時代，反導防御武器越來越追求命中精度，其中最有代表性的就是動能攔截器(KKV)[1-2]。KKV飛行速度高達5馬赫以上，飛越大氣層時的強烈氣動加熱會降低其攜帶的紅外導引頭的尋的精度。THAAD、SM-2等武器型號都采用導引頭側窗探測(SWD)技術來降低氣動加熱對探測精度的影響[3-4]。所謂的側窗探測，就是將導引頭安裝在KKV的側面。國外關于SWDKKV的公開文獻[3-4]極少，它們只是針對側窗的原理進行了一些討論。國內近年來開展了一些研究。文獻[5]考慮冷卻問題對側窗口進行了設計。針對側窗探測角度的選取問題，有相關文獻也進行了討論[6-7]。針對姿態定向問題，文獻[8-9]分別基于開關曲線方法與脈沖頻率調制(PWPF)方法開展了研究。針對SWDKKV的末段軌控方案的設計問題，國內外還未有公開文獻開展研究。

所謂軌控，就是通過推力器的輸出實現制導律。數十年來，制導律飛速發展，出現了諸如比例制導律(PNGL)[10]、一體滑模制導律(ISMGL)[11]、有限時間收斂制導律(FTCGL)[12]等許多或容易實現或性能優良的制導律。但現有制導律都需要執行機構輸出大小與方向都能變化的力。SWDKKV的推力器是捷聯在本體上的，其輸出具有兩個特性：首先，輸出是大小恒定的開關推力；其次，側窗探測要求姿態定向，推力器又是捷聯在本體上的，輸出力的方向只能與視線方向處于一定夾角范圍內。在現有方法中，脈寬調制(PWM)方法可將定常推力通過數字化的方法變換為變化推力[13]。但是PWM方法較為復雜且對于燃氣流率的穩定性要求很高。再者，即使推力大小可變化，姿態定向也使得推力無法隨意指向傳統制導律給出的指令方向。

針對以上所述問題，本文基于變結構控制理論設計了一種bang-bang切換形式的末段噴氣方案，適用于SWDKKV姿態定向且推力大小定常的情況。通過設置滑模死區減小了噴氣消耗，然后對死區的參數取值與脫靶量的關系進行了研究。最后采用數學仿真驗證了本文所提出方案的有效性。

1　側窗約束動能攔截器軌控模型

如圖1所示，OXYZ為末制導開始時的慣性坐標系，Ox2y2z2為視線坐標系。O與T分別為導彈與目標的質心。Ox2軸與視線軸重合且指向目標為正，Oy2軸處于垂直平面內且與Ox2軸垂直，Ox2軸與Oy2軸由右手準則確定Oz2軸。OXYZ與Ox2y2z2之間通過視線俯仰角φ與視線方位角θ進行轉換。可以給出三維相對運動方程[14]：

(1)

式中r為相對距離；aMr、aMφ、aMθ分別為導彈控制加速度在Ox2軸、Oy2軸及Oz2軸上的投影；aTr、aTθ、aTφ、Fr、Fθ、Fφ分別是目標機動加速度、氣動加速度在各視線坐標軸上的投影。

(2)

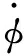
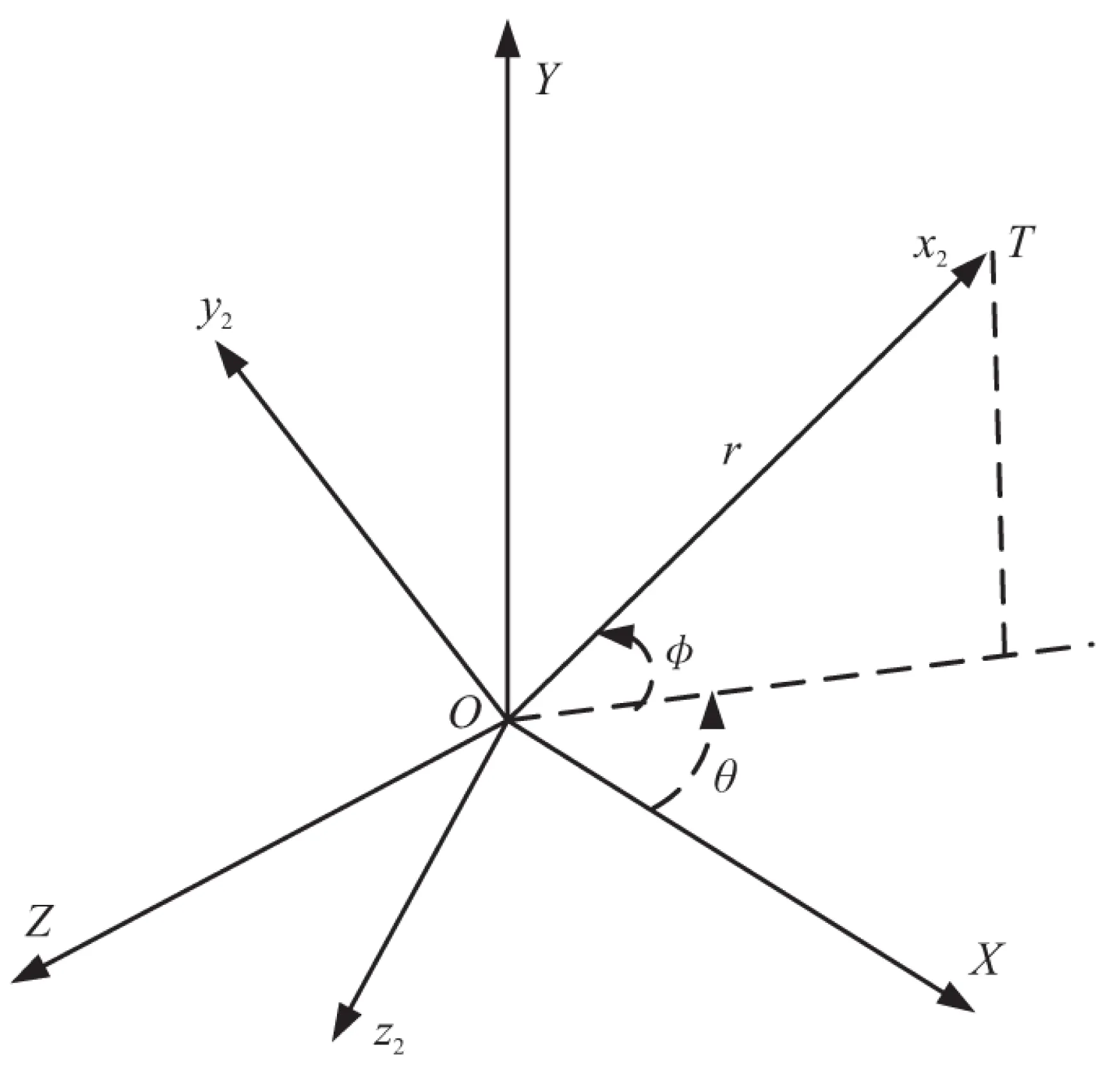
圖1　導彈-目標三維運動關系

首先給出側窗定向下坐標系的轉換關系，如圖2所示，視線坐標系Ox2y2z2，導彈本體坐標系Ox1y1z1。坐標系Ox1y1z1與Ox2y2z2相互轉換的角度為高低角ε、偏航角β及滾轉角γ。姿態定向完成后：|ε|≤εs，|β|≤βs，γ≈0。εs與βs的大小由側窗的大小及姿態定向的精度共同決定。

圖2　姿態約束關系

坐標系Ox2y2z2與Ox1y1z1的轉換關系為

(3)

SWDKKV的推力器是捷聯在本體上的，如圖3所示。從導彈尾部向前看，推力器可產生沿本體Oy1軸與Oz1軸的軌控力，有推力器1、2、3、4。

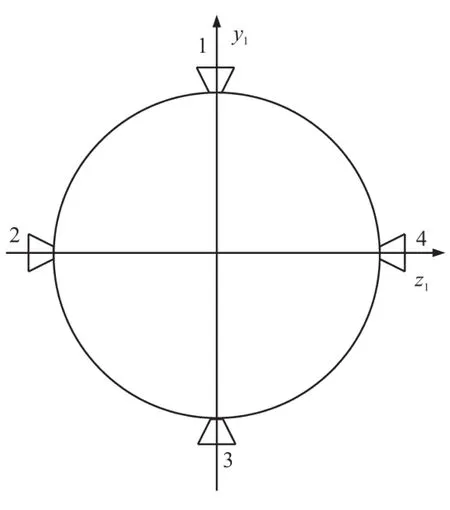
圖3　推力器布局

設本體系下推力F1：

(4)

其中

(5)

式中Ωy、Ωz皆為正常值。

利用式(3)可將推力F1轉換到視線系Ox2y2z2，得到視線系下的推力F2：

(6)

加速度a2=F2/m=[ax2ay2az2]。由坐標系定義可知a2就是導彈控制加速度在視線系Ox2y2z2下的投影，同時考慮姿態定向完成后γ≈0，可得

(7)

一般來說，由制導律給出的加速度指令的方向與大小都是變化的。然而由式(7)可看出，導彈的控制加速度的大小與方向都是受限的，無法實現傳統制導律。下面將介紹一種適合于SWDKKV特點的軌控方案。

2　末段軌控方案

2.1無噴氣死區的變結構方案

選取滑模面為

(8)

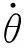
(9)

接下來由定理1給出本文所設計的軌控方案及穩定性結論。

定理1：考慮制導系統(2)，選取滑模面(8)，軌控噴氣規律取式(10)：

(10)

其中

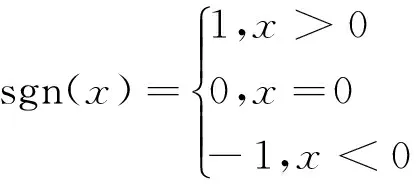
(11)

如果式(12)與式(13)成立，則有限時間內s1=s2=0。

(12)

(13)

證明：

取Lyapunov函數：

(14)

將式(14)對時間求導，同時考慮式(9)可得

(15)

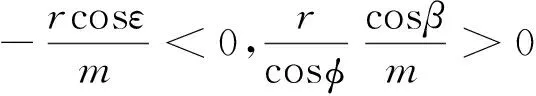
2.2有噴氣死區的變結構方案

為了降低噴氣量，設置滑模死區：

(16)

其中，k1、k2、ε1及ε2都是正常數，對于末制導來說cosφ>0，則δ1>0且δ2>0。

由定理2給出具有滑模死區的噴氣律及穩定性結論。

定理2：考慮制導系統(2)，選取滑模面(8)，軌控噴氣規律取式(17)：

(17)

這里

(18)

其中，δ1與δ2由式(16)給出。如果式(12)與式(13)成立，則有限時間內|s1|≤δ1且|s2|≤δ2。

注：下面分析死區的參數與脫靶量的關系。

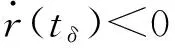
下面的分析中認為假設1成立。合理設計參數，軌控噴氣規律取式(17)，由定理2可得

(19)

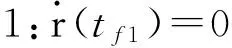
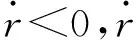
(20)

考慮式(1)可得

(21)

式中Fr/m為氣動所形成的加速度。

定義

(22)

式中max{x}為x的最大值；f為正常數。

結合式(1)與式(22)可得

(23)

由定義1可知r(tδ)是r在tδ≤t≤tf1時間段內的最大值，可推知：

(24)

結合式(20)與式(24)可知：

(25)

將式(25)在tδ到t上進行積分，可得

(26)

由于r(tδ)、k1及k2為正常數，可推知：

(27)

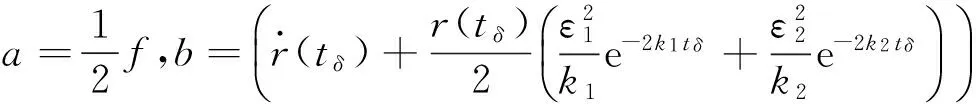
(28)

令c=r(tδ)，將式(28)在tδ到t(tδ≤t≤tf1) 積分，可得

(29)

下面分a>0與a=0 2種情況討論參數k1、k2、ε1及ε2對命中精度的影響。

(1)當a=0

由a=0及式(28)可得

(30)

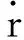
a=0對應著側窗定向角度為0，重力在視線上的作用為0，目標機動在視線上的分量為0及氣動力在視線上的分量為0的絕對理想情況。

(2)當a>0

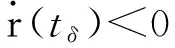
(31)

結合式(29)與式(31)可知

(32)

(33)

總之，可得到這樣的結論：只要選取足夠大的k1、k2及足夠小的ε1與ε2，就能在設置死區的同時獲得足夠小的脫靶量。當然，由式(16)可知，k1越大k2及ε1與ε2越小時，相應的滑模死區就越小，對于噴氣量的節約效果就越小。因此必須合理設計參數，在節約噴氣量與命中精度之間尋求平衡。

3　仿真驗證

仿真結果由圖4～圖9給出，詳細的脫靶量與推力器的噴氣消耗由表1給出。由圖4與圖5可見，在不設置滑模死區時，滑模面與視線角速率都能在命中目標之前快速收斂到0。由圖7與圖8可見，在設置滑模死區的情況下，滑模面與視線角速率都能在命中目標之前收斂到0附近。由圖6可見，在沒有設置滑模死區時，推力器密集地開啟與關閉。而由圖9可見，在設置了滑模死區后，推力器開關次數明顯減少，在部分時間段內，推力器甚至保持關閉狀態。

由表1可見，無論是否設置滑模死區，脫靶量都能滿足直接撞擊的精度要求。在設置了滑模死區后，無論是推力器開關次數還是消耗的比沖都明顯下降。

從仿真結果分析可知，本文所提出的軌控方案式(10)可有效完成SWDKKV的軌道控制任務，而進一步提出的滑模死區式(16)不僅可完成軌道控制任務，而且可降低推力器的噴氣消耗量。

(1) 無死區

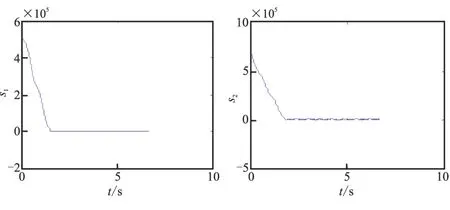
(a)s1　　　　　　　　　　(b)s2

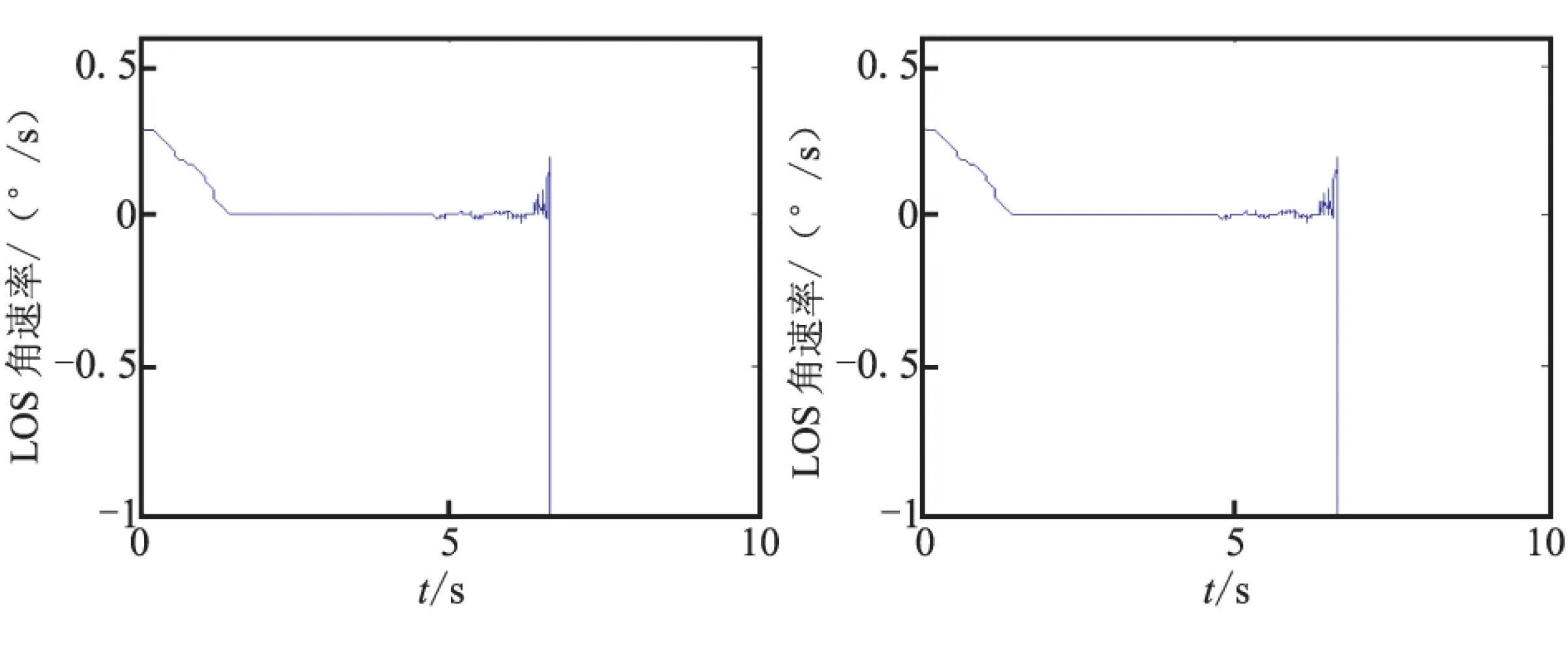
圖5　視線角速率

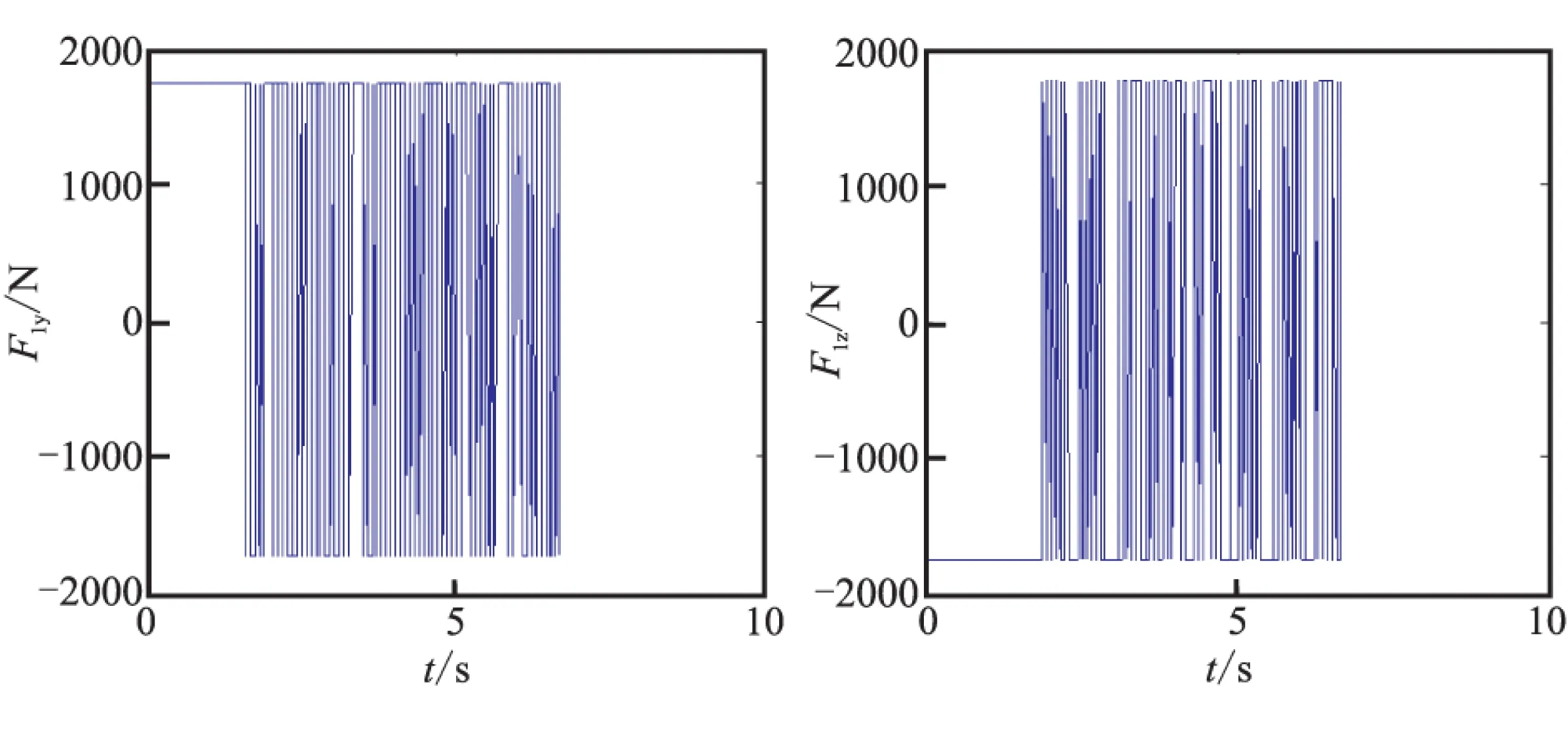
(a)F1y　　　　　　　　　　(b)F1z

(2)有死區

(a)s1　　　　　　　　　　　(b)s2

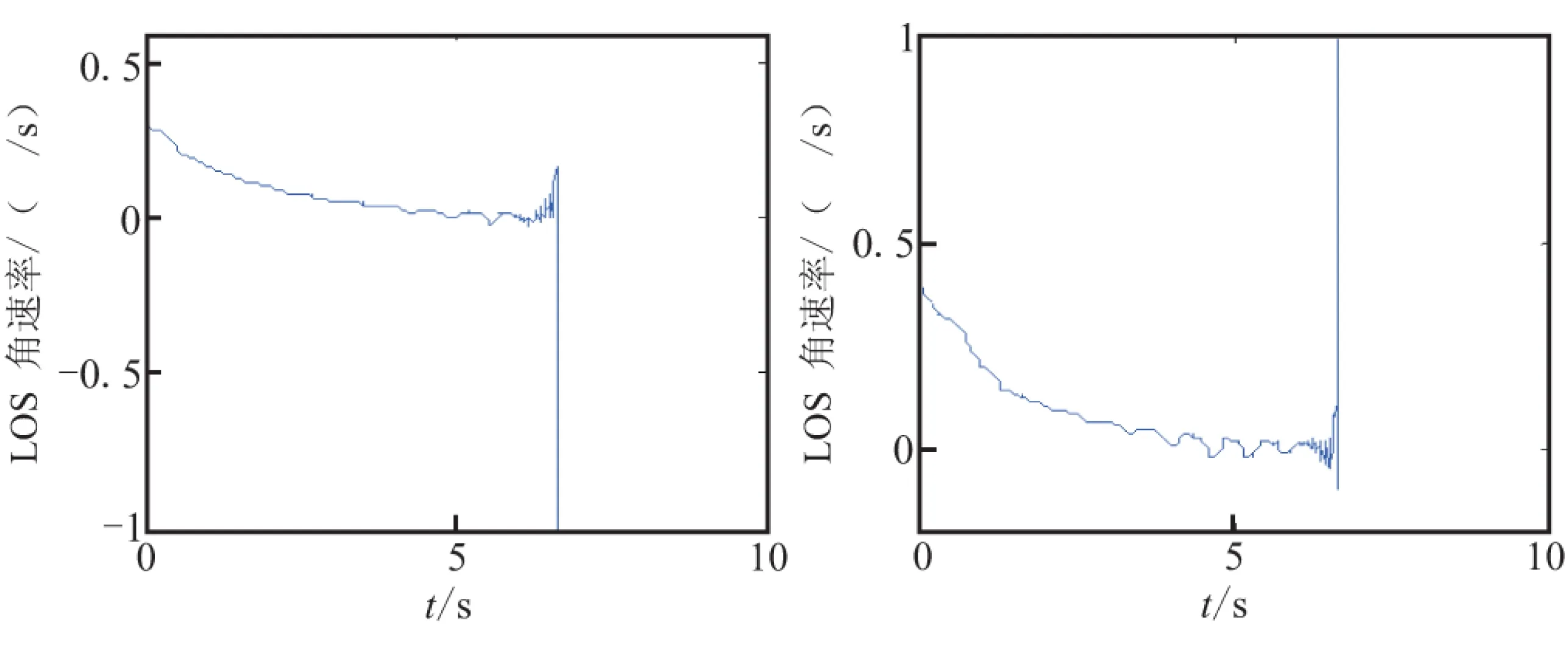
圖8　視線角速率

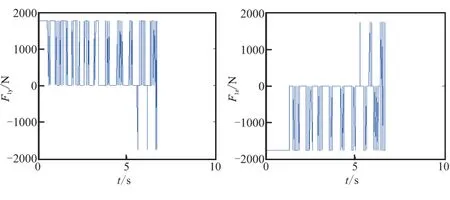
(a)F1y　　　　　　　　　　　(b)F1z

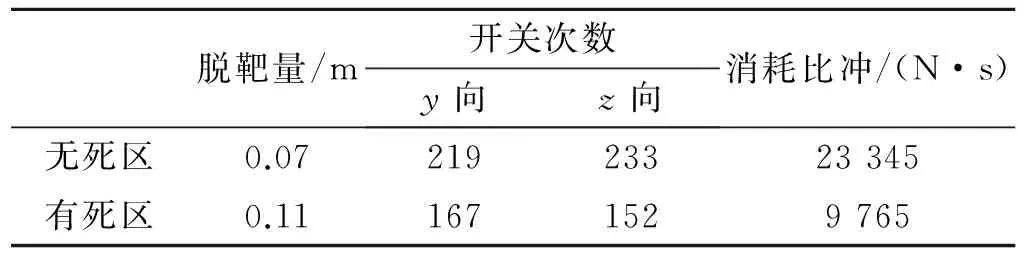
表1　仿真結果

4　結論

(1)提出的軌控方案可有效解決SWDKKV的軌道控制問題。在所考察的飛行任務中，綜合考慮了目標機動、姿態定向偏差、氣動干擾以及噴氣周期，結果表明軌控精度可滿足直接撞擊的任務要求。

(2)提出的軌控方案是bang-bang形式的，符合推力器的工作特性，因而所提出的方案具有良好的工程可實現性。

(3)提出的滑模死區不僅可大幅降低推力器的噴氣消耗，而且還能取得良好的軌控精度。同時，也降低了推力器開關的次數，提高了推力器的可靠性。

[1]張宏安,葉定友,郭彤.固體動能攔截器研究初探[J].固體火箭技術,2002,25(4):6-8.

[2]陸亞東,楊明,王子才.固體動能攔截器助推段飛行方案研究[J].固體火箭技術,2006,29(3):157-160.

[3]Leary A,Watson W,Florie D,et al.Test& evaluation facility for thaad IR seekers [J].SPIE,2004,2474:172-177.

[4]Strauss B J,Gravina R J,Hasenzahl C J,et al.All attitude guidance and control for endoatmospheric intercepts [C]//AIAA SDIO Annual Interceptor Technology Conference,AIAA 93-2643,1993.

[5]楊曉潁,劉純勝,顧永其.高速飛行器紅外制冷頭罩設計[J].紅外與激光工程,2004,33(6):576-579.

[6]張洪波,郭振云,湯國建.大氣層高層動能攔截器側窗探測方位研究[J].國防科技大學學報,2008,30(6):34-38.

[7]Yang Bao-qing,Zheng Tian-yu.Zhang Si-lun.Analysis and modeling of terminal guidance system for a flight vehicle with side-window detection [C]//Proceedings of the 33rd Chinese Control Conference,Nanjing,China,2014.

[8]張洪波,郭振云,湯國建.大氣高層具有側窗的動能攔截器的數學仿真 [J].系統仿真學報,2007,19(23):5383-5385.

[9]Lu Cang-hai,Cai Yuan-li.Side-mounted window orientation algorithm and attitude controller design for kinetic kill vehicle [C] //Proceedings of the Fourth International Conference on Instrumentation and Measurement.Computer,Communication and Control,2014.

[10]Ghawghawe S N,Ghose D.Pure proportional navigation against time-varying target maneuvers [J].IEEE Transaction on Control Systems Technology.1999,22(4):589-594.

[11]Zhang Zhen-xing,Li Shi-hua,Luo Sheng.Composite guidance laws based on sliding mode control with impact angle contraint and autopilot lag [J].Transaction of the Institute of Measurement and Control,2013,35(6):764-776.

[12]Zhou Di,Sun Sheng.Guidance laws with finite convergence [J].Journal of Guidance.Control and Dynamics,2009,32(6):1838-1846.

[13]常桁,王一白,劉宇.基于PWM 原理的固體姿態控制系統實驗研究 [J].固體火箭技術,2013,36(5):608-612.

[14]Ma Ke-mao,Zhang Xiao-yu.A novel guidance law with line-of-sight acceleration feedback for missiles against maneuvering targets [J].Mathematical Problem in Engineering,2014:1-8.

(編輯：呂耀輝)

Orbit control scheme of the terminal course of side window detection kinetic kill vehicle

WANG Yang1，ZHOU Jun1，ZHAO Bin1，YOU Yu-hua2

(1.Institute of Precision Guidance and Control,Northwestern Polytechnical University Xi’an710072；2.China Academy of Launch Vehicle Technology，Beijing100076)

In terms of the orbit control problem of the terminal course of side window detection kinetic kill vehicle(SWDKKV),this article puts forward a new rail control scheme based on the variable structure control theory.First of all,an orbit control model under three dimensional space was established after considering the restraints of side window.Subsequently,a new type of sliding mode surface with variable structure was presented based on such features of side window detection kinetic kill vehicle as being only able to output constant switching thrust and having directional attitude constraints,and a bang-bang type of orbit control scheme suitable for terminal intercept was designed.Lyapunov stability theory was adopted to strictly prove the stability of the proposed methods.In order to reduce jet consumption,a sliding dead zone was designed and the value range of parameters in sliding dead zone which can ensure hitting accuracy was studied.Simulation results show that the designed orbit control scheme can meet the accuracy requirements while sliding dead zone can reduce jet consumption.

side window detection；kinetic kill vehicle；terminal guidance；orbit control scheme；sliding mode control；sliding dead zone

2015-06-04；

2015-06-23。

國家自然科學基金(61104194)；西北工業大學基礎研究基金資助項目(JCT20130101)。

王洋(1989—)，男，博士生，研究方向為導航制導與控制。E-mail：zjt219571@163.com

V438

A

1006-2793(2016)04-0588-06

10.7673/j.issn.1006-2793.2016.04.025