帶末端角度約束的空地反輻射導彈被動制導律

李　解，雷虎民，李　炯，翟岱亮

(空軍工程大學 防空反導學院，西安　710051)

?

帶末端角度約束的空地反輻射導彈被動制導律

李解，雷虎民，李炯，翟岱亮

(空軍工程大學 防空反導學院，西安710051)

針對被動跟蹤問題，結合UKF和PF濾波各自優點，采用了UPF濾波器對彈目相對運動信息進行了精確估計。針對濾波器估計過程中，對系統狀態可觀測性的要求，在分析了系統可觀測條件的基礎上，結合空地反輻射導彈特點，設計了一種帶末端角度約束，且能夠增強系統狀態可觀測性的被動制導律。仿真結果表明，UPF濾波器結合所設計的被動制導律能有效準確地估計彈目相對運動信息，實現了精確制導，同時能有效地約束末端攻擊角度，保證了空地反輻射導彈的殺傷效果。

末端角度約束；UPF濾波；滑模制導律；被動制導

0　引言

由于空地反輻射導彈僅安裝有被動雷達導引頭，且僅能測得目標相對導彈的方位角，測角誤差大，因此導彈并不能準確獲得目標位置信息。在僅有方位測量的情況下對目標進行探測跟蹤的問題被稱為“被動跟蹤”問題，而利用被動跟蹤所獲得的信息進行制導的問題被稱為“被動制導”問題。

對于被動跟蹤問題，目前比較常見的是采用卡爾曼濾波器通過純方位測量對目標信息進行估計。文獻[1]采用了EKF濾波器，文獻[2]采用了擴張狀態觀測器，均取得了比較好的估計效果。但是，由于反輻射導彈被動雷達導引頭測角誤差較大，上述方法估計精度并不能滿足制導精度的要求，故本文結合UKF和PF兩種濾波器的特點，采用UPF濾波器對目標信息實施估計，在較大的測量噪聲下仍可保證濾波精度。

對于空地反輻射導彈被動制導問題，需要考慮兩個問題。第一是濾波器的可觀測性問題，可觀測性反映測量值對系統狀態的觀測能力，將直接影響估計效果。針對這個問題，文獻[3]和文獻[4]各自分析了被動跟蹤系統的可觀測性，提出了導彈適度機動從而提高狀態可觀測性的觀點。第二個問題是滿足反輻射導彈打擊要求的末端攻擊角度約束，這類問題研究成果很多，如文獻[5]提出的彈道成型制導律，如文獻[6]提出的滑模制導律等等。本文的主要工作是將被動制導問題所涉及的兩個問題綜合考慮，設計一種即能保證狀態可觀測性，又保證末端角度約束的空地反輻射導彈被動跟蹤制導律。

1　純方位測量的彈目相對信息估計

在被動制導過程中，彈目相對距離、相對速度等信息需要通過非線性濾波器來估計。綜合UKF濾波和PF濾波的特性，本文采用UPF濾波作為彈目相對運動信息的估計手段。

1.1估計系統的建立

靜止目標被視為地面上靜止不動的質點，其坐標為Xt=[xt，yt，zt]T。

設目標真實坐標為Xt0=[xt0，yt0，zt0]T，則在導彈發射時，由載機裝訂的目標初始坐標為

(1)

式中ν0為載機雷達觀測噪聲。

式(1)表明載機裝訂的目標初始位置帶有誤差。

設在慣性坐標系中反輻射導彈的坐標為Xm=[xm，ym，zm]T，靜止目標雷達的坐標為Xt=[xt，yt，zt]T，選取狀態變量為目標雷達對反輻射導彈的相對坐標Xr=[xr，yr，zr]T，即

(2)

系統的狀態方程和量測方程可分別描述為

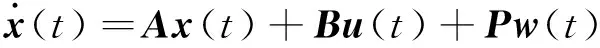
(3)

其中

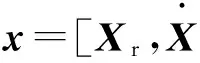
被動導引頭的量測模型：

(4)

(5)

(6)

式中θL、ψL為視線傾角和視線偏角；ν1、ν2為被動雷達導引頭量測噪聲；Xr=Xt-Xm=[xr，yr，zr]T。

1.2UPF濾波算法

Bayes估計理論所推導出的時間更新方程和測量更新方程是一種最優估計。其方程形式雖然簡單，但是一個高維積分方程，一般并不能顯式地表達出來。

針對非線性系統，主流的Bayes估計數值計算方法分為高斯假設參數化方法的非線性卡爾曼濾波EKF和UKF，以及貫序蒙特卡洛方法的粒子濾波PF。

非線性卡爾曼濾波中，EKF通過對非線性系統狀態方程和測量方程進行一階泰勒展開，將非線性問題轉化為線性問題，當系統非線性較強時，濾波穩定性和精度將大幅度下降。UKF通過對無跡變換(Unscented Transform)，在假設狀態高斯分布的前提下，對狀態進行sigma采樣，從而近似狀態的概率密度分布，具有良好的非線性和濾波精度。

故本文結合UKF和PF的優點，利用UKF代替建議分布進行重要性采樣，即利用UKF來預測下一個粒子，每個粒子的建議分布如下：

(7)

UPF的計算過程如下：

(1)初始化

從先驗概率分布p(x0)中抽取N個粒子：

(8)

(9)

(2)重要性采樣

通過建議分布：

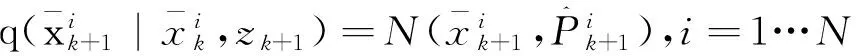
(10)

計算重要性權值：

(11)

并歸一化：

(12)

(3)重采樣

重采樣過程依據重要性權值，復制權值大的粒子，丟棄權值較小的粒子，以消除粒子的退化現象，使其分布符合狀態轉移概率分布的變化。粒子復制完畢后，賦予每個粒子等權值：

(13)

(4)狀態輸出

(14)

狀態均值：

(15)

2　被動跟蹤系統可觀測性分析

空地反輻射導彈被動跟蹤依賴濾波器對彈目相對運動信息的估計，濾波效果對導彈能否實現精確制導顯得尤為重要。濾波效果的好壞，除了與濾波器本身性能和導引頭噪聲大小有關外，還取決于被動跟蹤系統的可觀測性強弱。

被動跟蹤系統的測量是非線性的，而非線性系統的可觀測性如下定義：

當存在有限時刻t>t0時，若其Grammian矩陣：

D(t，t0)=∫t0tΦT(t，t0)HT(t)H(t)Φ(t，t0)dt

(16)

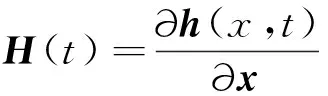
根據式(3)求得被動跟蹤系統的狀態轉移矩陣：

(17)

根據式(4)求被動跟蹤系統的測量矩陣其形式復雜，現將式(4)進行線性化：

(18)

令

(19)

再對M0(t)進行變換，推導出：

(20)

則非線性測量模型可寫成如下線性形式：

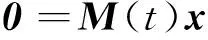
(21)

對于式(3)和式(21)所描述的系統，若系統在時間區間(t0，t)上狀態是可觀測的，則其Grammian矩陣：

D(t，t0)=∫t0tΦT(t，t0)MT(t)M(t)Φ(t，t0)dt

(22)

是正定的。其等價描述是，矩陣M(t)Φ(t，t0)的列向量線性無關[8]。

任取列向量α=[a1，a2，a3，a4，a5，a6]T，ai不全為0，若M(t)Φ(t，t0)的列向量線性無關，則

(23)

將α帶入式 (23)，得

(24)

(25)

考慮式(21)，得

(26)

(27)

由系統狀態方程，可得

(28)

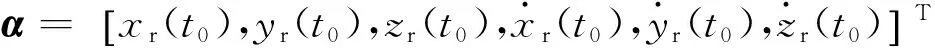
(29)

結合式(26)～式(28)，得

(30)

若上式成立，則式(23)成立，即M(t)Φ(t，t0)的列向量線性無關。此時，系統的Grammian矩陣D(t，t0)正定，系統是可觀測的。

而式(3)中：

(31)

式中θvm、ψvm為彈道傾角和彈道偏角；amy、amz為導彈在俯仰平面和偏航平面的加速度。

若式(30)成立，則

(32)

進而推得

(33)

從上式可得出結論，若要使濾波器在導彈制導過程具有良好的估計精度，則制導過程中要保持一定的視線角變化率。

3　帶末端角度約束的滑模制導律設計

本文考慮到空地反輻射導彈末制導對末端角度約束的要求以及濾波器可觀測性的要求，參考文獻中運動跟蹤滑模制導律的思想[9]，設計一種既保證末端角度約束，又保證視線角變化的制導律。

3.1三維彈目相對運動模型

彈目相對運動關系如圖1所示。

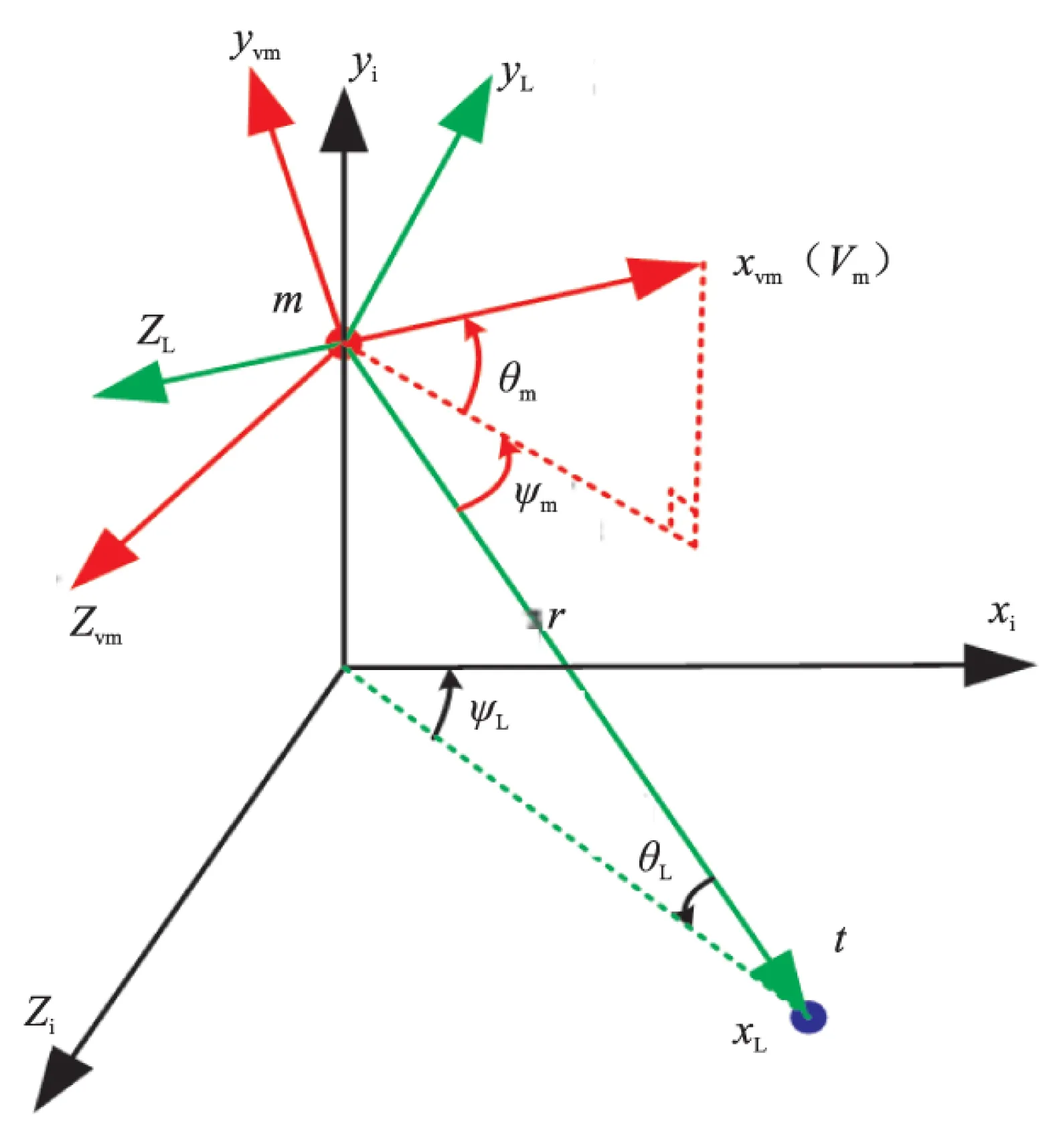
圖1　彈目相對運動關系

圖1中，xiyizi為慣性坐標系；xLyLzL為視線坐標系；xvyvzv為彈道坐標系；m為導彈；t為目標；θL、ψL分別為視線傾角和視線偏角；θm、ψm分別為導彈相對視線坐標系的傾角和偏角。

設導彈的速度為Vm，amy和amz分別為導彈在俯仰平面和偏航平面的加速度，目標視為地面靜止目標，彈目相對距離為r。

由圖1可得

(34)

(35)

(36)

(37)

(38)

對式(35)、式(36)求導結合式(37)、式(38)得

(39)

(40)

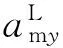
3.2俯仰平面制導律設計

考慮制導律設計對末端角度約束及狀態可觀測性的要求，令

(41)

(42)

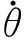
選取滑模面為

s=k1|x1|γsgn(x1)+k2x2

(43)

參數k1>0，k2>0，0<γ<1。

根據滑模變結構控制理論，為保證系統狀態平穩接近滑模面進入滑動模態，采用趨近律方法推導制導律。選取趨近律：

(44)

由式(43)、式(44)，可得

(45)

由于r>0，所以

(46)

根據滑模變結構控制理論，系統狀態將在有限時間內到達滑模面。

對式(43)求導：

(47)

由式(46)，可得

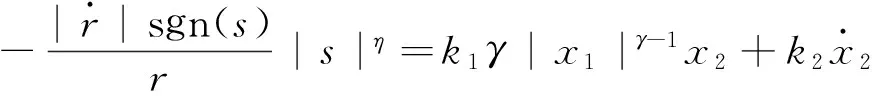
(48)

將式(39)帶入式 (48)，可得

(49)

從而推得制導律：

(50)

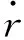
(51)

(52)

(53)

(54)

(55)

3.3偏航平面制導律設計

偏航平面制導律設計不考慮末端角度約束，為保證整個制導系統的穩定性，偏航平面制導律的設計基于零化視線角速率的思想設計。

令

(56)

選取滑模面：

s=x3

(57)

選取趨近律：

(58)

參數k3>0，0<α3<1。則根據式(40)和式(58)可推導出偏航平面制導律：

(59)

所需制導信息同樣由濾波器估計獲得。

4　仿真分析

UPF濾波器粒子數N=100，協方差陣初值取P0=diag(1002，102，1002，102，102，102)，過程噪聲方差cov(ω)=0.0012，測量噪聲方差cov(ν)=2.25(°)2。

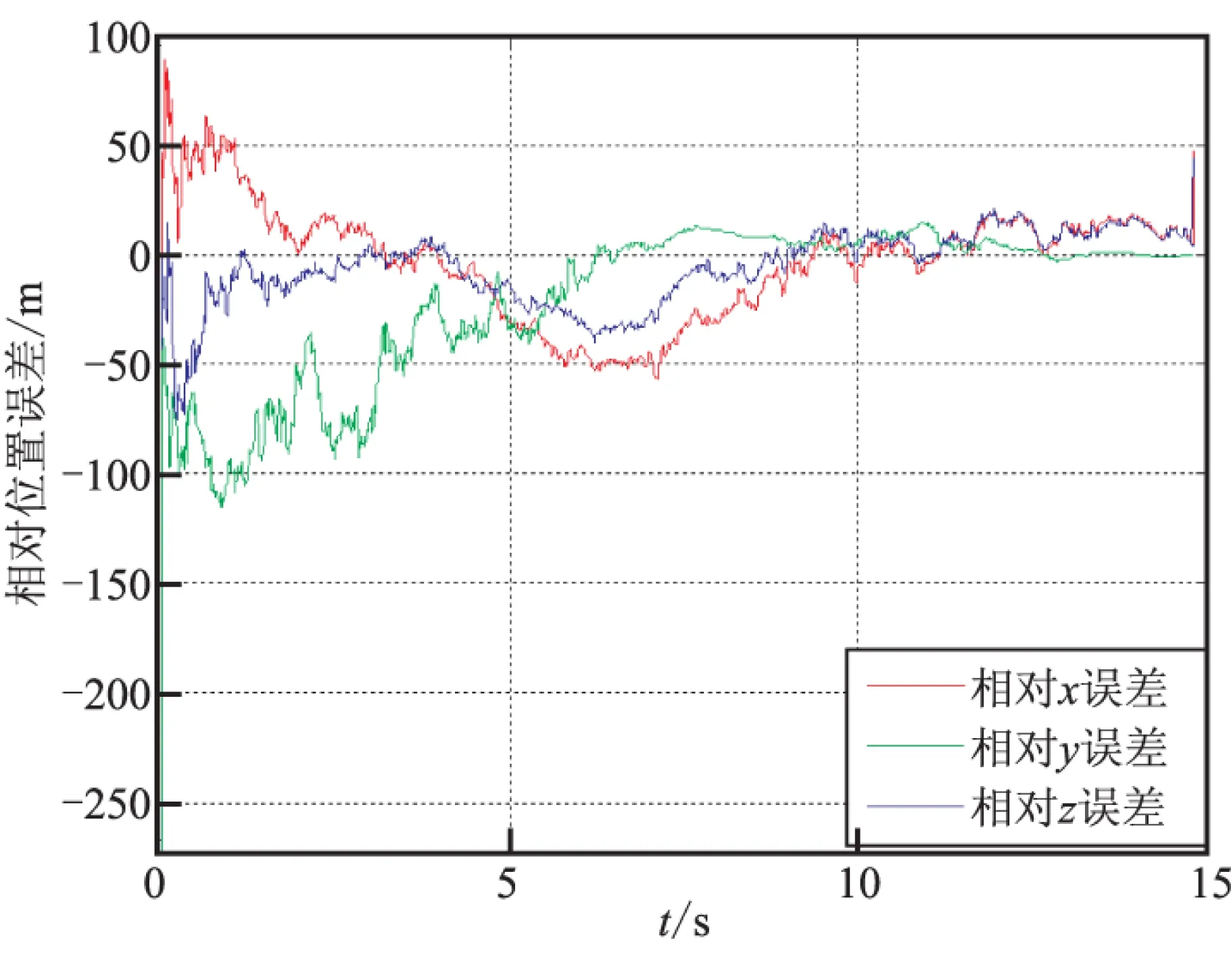
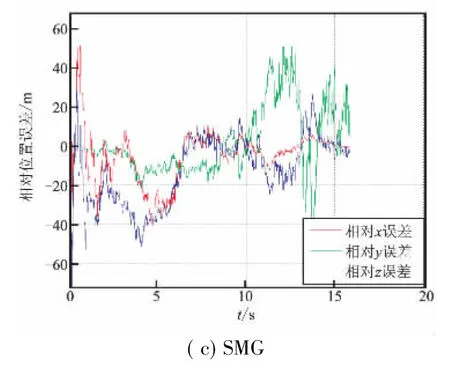
為對比驗證，仿真中采用3種帶末端角度約束的制導律，分別為本文所設計的制導律，文獻[5]所述的彈道成型制導律(TSG)，文獻[6]所述的滑模制導律(SMG)。3種制導律作用下濾波器對彈目相對坐標的估計誤差如圖2所示。

(a)本文設計的制導律

(b)TSG

(c)SMG

從圖2(a)可看出，目標位置X坐標、Y坐標、Z坐標均能準確收斂。

圖2(b)、(c)與圖2(a)相比，無論是TSG還是SMG，其估計收斂效果均不如本文所設計的制導律。因為濾波器估計效果好壞的關鍵就在于系統可觀測性的強度，而本文所設計的制導律可有效提高系統的可觀測性，故效果優于其他兩種制導律，制導精度也進一步提高。制導精度對比見表1。

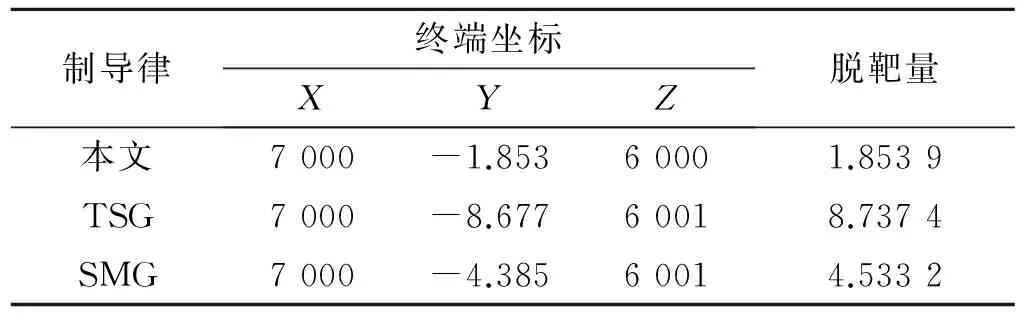
表1　3種制導律制導精度對比

圖3～圖5是濾波器對視線傾角、視線偏角和彈目相對速度等制導律所需信息的估計誤差。由圖可看出，3種信息誤差均迅速收斂，保證了制導指令的準確性。

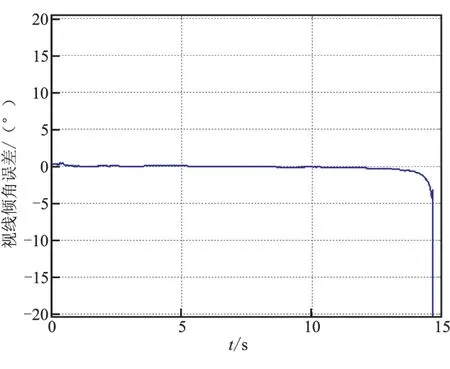
圖3　視線傾角誤差

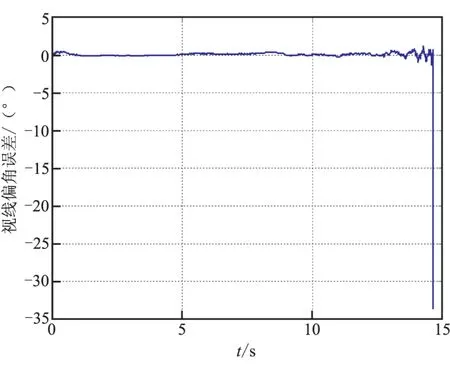
圖4　視線偏角誤差

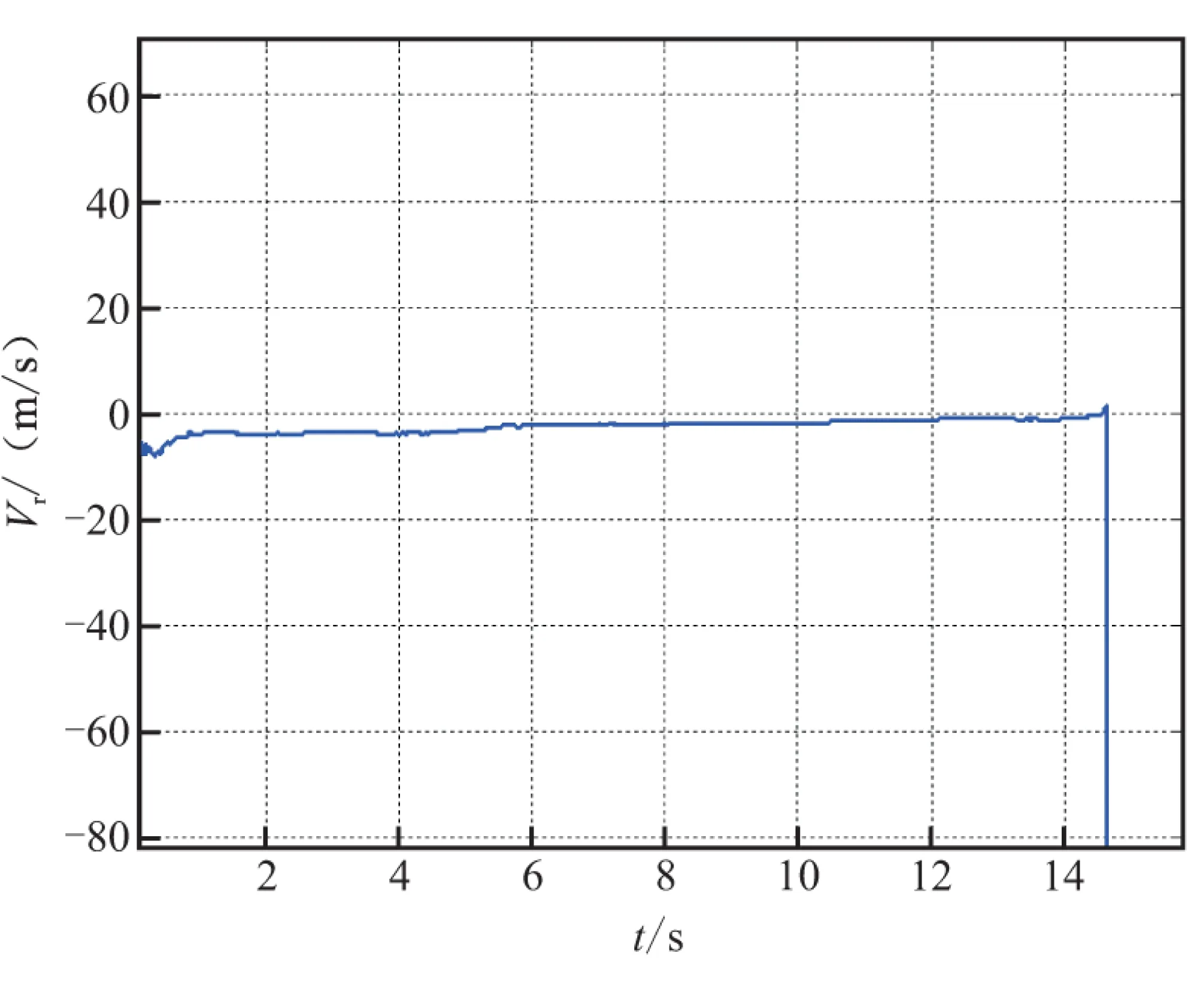
圖5　相對速度誤差

圖6反映視線傾角的變化，從圖6可看出，在給定末端角度約束為-80°的情況下，所設計制導律可保證導彈以期望角度攻擊目標。圖7反映視線傾角速率隨時間的變化，由圖7可見，視線傾角速率能夠按照期望的視線傾角速率運動，從而保證了系統的可觀測性，即保證了濾波器狀態估計的準確性。

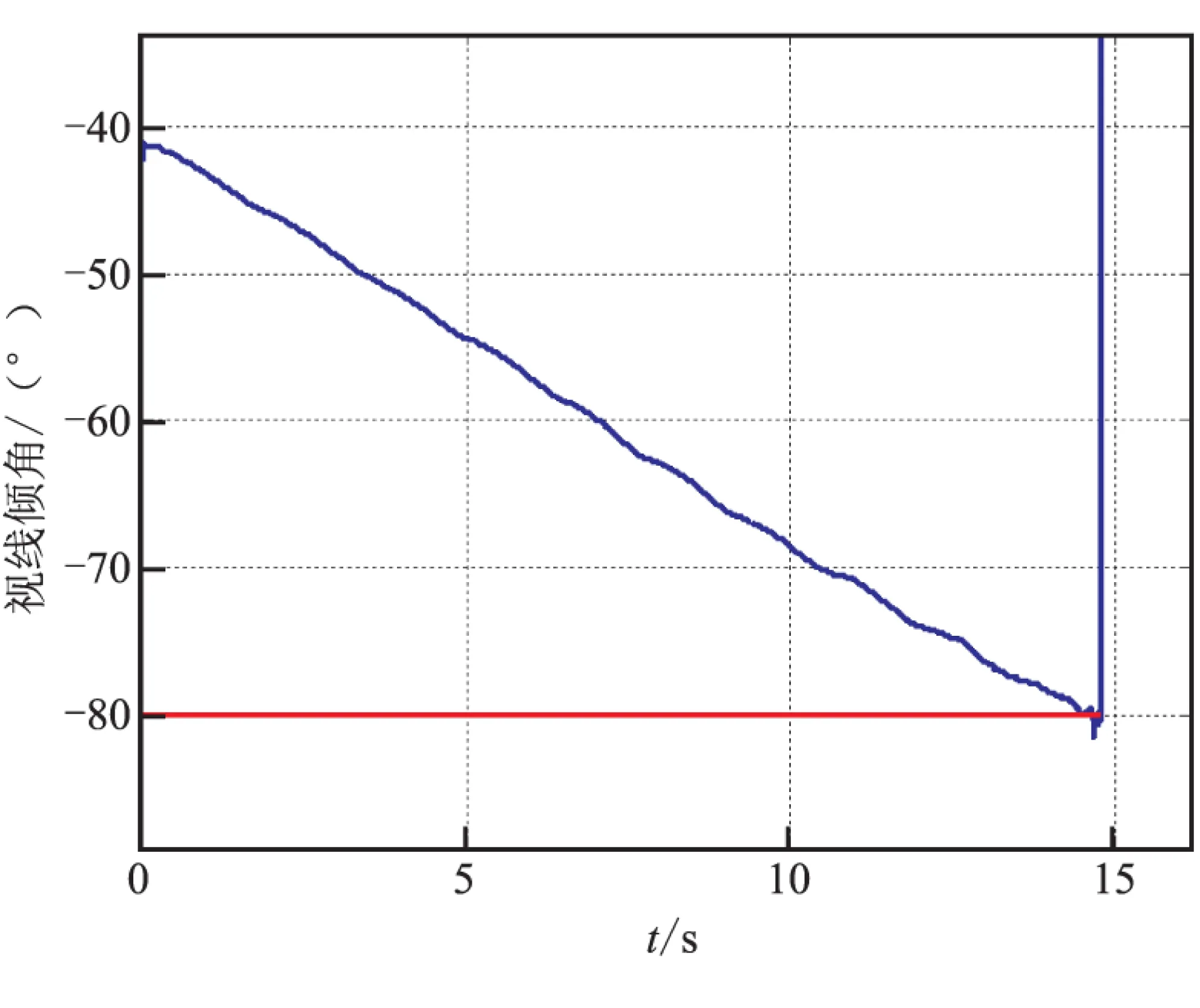
圖6　視線傾角

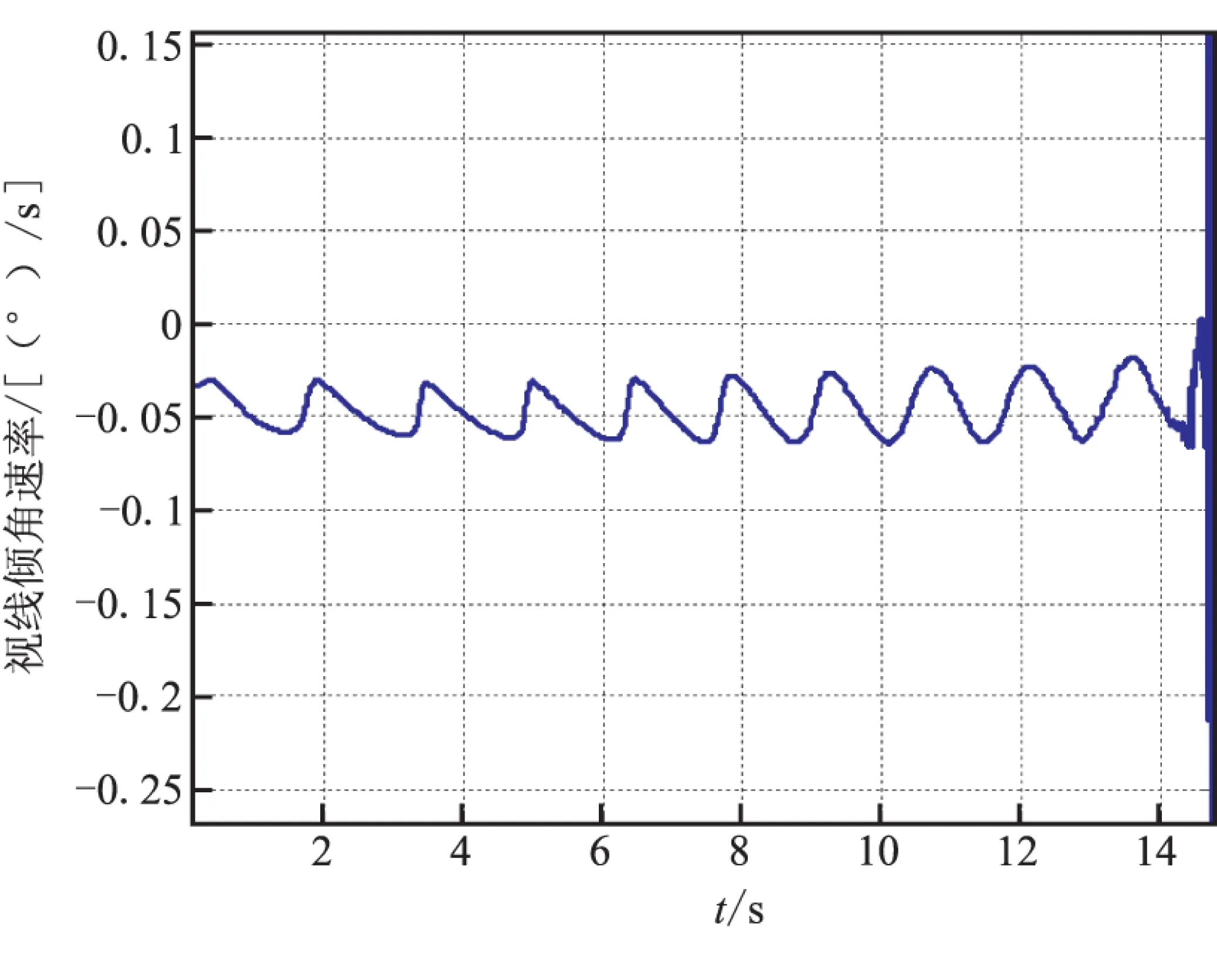
圖7　視線傾角速率

5　結論

(1)本文結合UKF和PF濾波器各自的特點，采用UPF濾波器對被動制導過程中所需的彈目相對信息進行估計，在所設計制導律的配合下，獲得了良好的估計效果。

(2)本文在分析了系統可觀測性的基礎上，設計了能夠有效保證系統可觀測性的制導律，從而保證了濾波器的估計精度。針對空地反輻射導彈的特殊性，所設計的制導律還能同時對末端角度起到良好的約束作用，保證了殺傷效果。

[1]魏玉樂,方群,羅建軍.彈目信息在純方位制導中的應用[J].西北工業大學學報,2005 ,23(5).

[2]馬克茂.帶有終端視線約束的非光滑制導律設計[J].彈道學報,2011,23(2).

[3]田宏亮,梁曉庚,賈曉洪,等.基于視線角速度的增強目標可觀性研究[J].彈道學報,2011,23(2).

[4]楊國勝,竇麗華,候朝楨.基于純角度的三維運動目標可觀性研究[J].兵工學報,2004,25(2).

[5]Paul Zarchan.Tactical and strategic missile guidance 6th edition [M].American Institute of Aeronautics and Astronautics,Inc.

[6]尹永鑫,楊明,吳鵬.針對機動目標帶攻擊角約束的三維制導律[J].固體火箭技術,2010,33(3).

[7]Julier S J,Uhlmann J K.Unscented filtering and nonlinear estimation[J].Proceedings of the IEEE,2004,92(3).

[8]Lim C C,Li M.Observability analysis of two closed-loop guidance systems with bearings-only measurements[J].Nonlinear Analysis:Real World Applications 1,2000.

[9]周荻.尋的導彈新型導引規律[M].北京:國防工業出版社,2002.

(編輯：呂耀輝)

Passive guidance law for air-to-ground anti-radiation missile with terminal angular constraint

LI Jie，LEI Hu-min，LI Jiong，ZHAI Dai-liang

(Air Force Engineering University Air and Missile Defense College，Xi’an710051，China)

For passive tracing problem,combined with the advantages of UKF and PF filters,an UPF filter was adopted to realize the accurate estimation of the information of missile-target relative movement.For the requirement of the observability of system states during estimating,combined with the characteristic of air-to-ground anti-radiation missile,a passive guidance law with terminal angular constraint and observability enhancement was designed.The simulation result shows that the UPF filter combined with the designed passive guidance law can estimate the relative information accurately and effectively and realize accurate guidance.Meanwhile, with effective terminal angular constraint,the damage effect of the missile is guaranteed.

terminal angular constraint；UPF filter；sliding mode guidance；passive guidance

2015-05-23；

2015-06-15。

航空科學基金(20140196004)；航空科學基金(20130196004)。

李解(1991—)，男，碩士生，研究方向為空天攔截器制導、控制與仿真。E-mail：sumffuk@163.com

V448

A

1006-2793(2016)04-0594-07

10.7673/j.issn.1006-2793.2016.04.026