“軸對稱”教學紀實與評析

張文靜　李偉榮

教學內容：人教版小學數學四年級下冊P82。

教學目標：

1.通過看一看、數一數的活動，進一步認識軸對稱圖形和對稱軸，探索軸對稱圖形的對稱點與對稱軸之間的關系。

2.通過觀察、操作等活動，能在方格紙上補全一個軸對稱圖形。

3.讓學生在探索的過程中進一步增強動手操作能力，發展空間觀念，培養審美觀念和學習數學的興趣。

教學重點：探索軸對稱圖形的對稱點與對稱軸之間的關系。掌握補全軸對稱圖形的方法。

教學難點：探索對稱圖形對應點特點，能準確地在方格紙上畫出軸對稱圖形的另一半。

教學流程：

一、課前交流，激發興趣

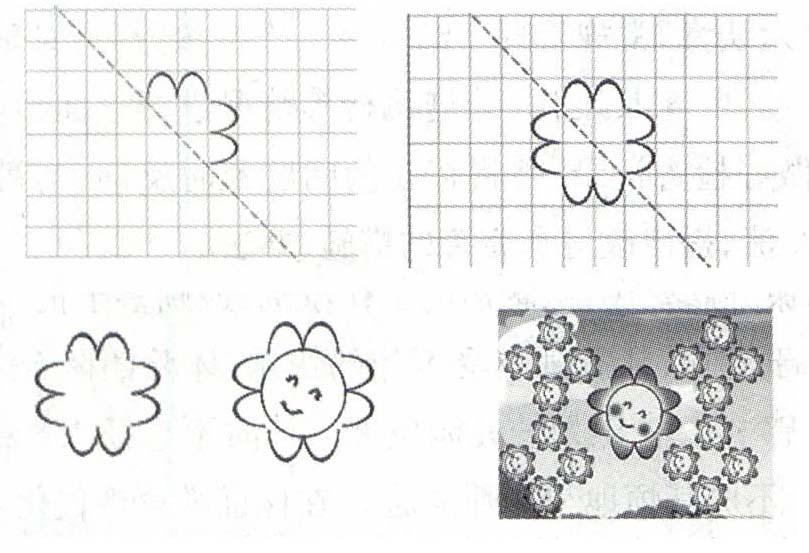
師：同學們，課前我們來做個數學游戲。它曾經是美國哈佛大學的測試題（出示題）。同學們仔細觀察，前幾幅圖有什么特點？

生：我發現它們都是對稱的。

師：那么在空白處我們接下來應該填什么樣的圖形呢？

生：填一個正6和一個反6。因為前面幾個圖形是正1和反1，正2和反2……所以空白處應該是正6和反6。

師：你很善于觀察，發現了圖形對稱的規律，現在我們開始今天的學習。

二、復習導入。回顧舊知

師：我們在二年級的時候學習過軸對稱圖形，請大家回憶一下什么是軸對稱圖形，并舉個生活中的例子。

生：把一個圖形沿著一條直線對折，兩邊完全重合，這樣的圖形就是軸對稱圖形。比如黑板的形狀是軸對稱圖形。比如課桌的形狀是對稱的。（學生舉例。）

師：生活中有很多物體的形狀是軸對稱圖形，那么這節課我們就在原來的基礎上，深入地研究軸對稱圖形。（板書課題：軸對稱。）

三、實踐反思。探究新知

1.學畫軸對稱圖形的對稱軸。

師：這些是生活中常見的軸對稱圖形，接下來請你們嘗試著畫出它們的對稱軸。

（學生訂正。）

師：現在我們隱去它們的顏色和圖案，再來看看，這些圖形又有幾條對稱軸？（課件：由圖案過渡到圖形。）

師：由此看來，有的圖形只有一條對稱軸，而有的圖形不只一條對稱軸。

2.探究軸對稱圖形的性質。

師：通過你的感覺來判斷，它是不是軸對稱圖形？你是怎么知道的？

生：沿著對稱軸對折、兩邊完全重合。

師：真善于運用。你是利用已有的軸對稱圖形的概念來進行判斷。在軸對稱圖形中，有很多像A和A′這樣的點，給它們取個名字，你想叫什么呢？

生：對稱點。

師：為什么？

生：因為在這個軸對稱圖形中，點A和點A′沿對稱軸對折后，能夠完全重合。

師：是這樣嗎？老師將屏幕上的圖形按比例縮小了。（在半透明紙上用紅筆標出這兩個點，沿對稱軸對折。）同學們看，這兩個點怎么樣了？兩邊的圖形呢？

生：重合了。

師：由此證明，剛才同學們的想象、猜測是正確的。就像同學們說的那樣，數學上把對稱圖形中沿對稱軸對折，能夠完全重合的點叫對應點。下面我們就從軸對稱圖形中最基本的對應點人手做進一步的研究。

師：在研究圖形與幾何的時候經常會用到格子圖，它便于我們觀察和研究。我們把小松樹放到格子圖中，研究一下對應點有什么特點。

師：拿出你的格子圖，你能嘗試著找出幾個小松樹的對應點嗎？想一想你可以怎樣找，再數一數、畫一畫，觀察這些對應點有什么共同的特點，把你的發現在小組中說一說。（出示學習要求，學生自主探索，小組交流。）

生1：我是用對折的方法找到點B的對應點B′的。

生2：我找的點B、點B′和他的位置不同，方法也不一樣。我是用數格子的方法找到點B和它的對應點B′的。我是這樣找的：先確定了點B，從點B向右數了2個格子就到了對稱軸；再從對稱軸開始向右再數2個格子，就找到了B′。

生3：我也用數格子的方法找的。我先從點C向右數了1個格子到了對稱軸；我又從點C′開始向左數了1個格子也到了對稱軸。還對折驗證了一下。

師：為同學們點贊，你們不僅表達流利，還很嚴謹。同學們找到了這么多對應點，觀察一下這些對應點，你有什么發現？

生：A點到對稱軸的距離是3小格，A′點到對稱軸的距離也是3小格，對應點到對稱軸的格子數量是相等的，我發現對應的兩個點到對稱軸的距離是相等的。

師：他是抓住了兩點到對稱軸的格子數量來研究發現的，誰的發現也是這樣的？（進行有效反饋。）還有別的發現嗎？

生：把對應點連起來，我發現這些連線都跟對稱軸垂直。

師：是這樣嗎？大家看看屏幕。（對應點連線，借助格子圖感知。）的確，對應點連線垂直于對稱軸。對應點到對稱軸的距離就是指從對應點到對稱軸的垂線段長度。

師：就像同學們發現的那樣，當A與A′點到對稱軸的距離相等，同時，它們的連線與對稱軸互相垂直，我們就說A與A′點是這個對稱圖形的一組對稱點。你還能找到其他對稱點嗎？（學生進行匯報。）

師：剛才同學們找到了很多組對稱點，也就是說任意一點都可以找到它的對稱點。那么由這些密密麻麻的對應點所連成的線段呢？

生1：由對應點連成的線段也是對應的。

生2：在對稱圖形中，對應點是對稱的，它們所連成的對應線段也是對稱的。

師：研究對稱圖形的對應線段時，不僅要考慮到長度，還要注意形狀。我們再來看，由這些線段所圍成的圖形呢？

生：都是軸對稱圖形。

師：你們由對稱點想到了線段，由對稱線段想到了對稱圖形。你們太了不起了！現在就拿起這個圖形，我們再次感受一下這些點、線、形沿對稱軸對折完全重合。（課件演示。）

師：我們借助于方格圖，通過尋找對稱點，再由點到線、到形，層層深入，共同去思考、去推理、去證明，總結發現了軸對稱圖形的特點是：對稱點到對稱軸的距離相等。（板書。）

3.補全軸對稱圖形。

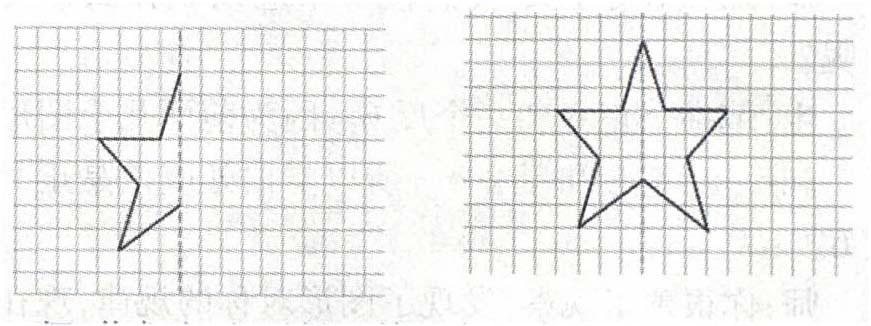
師：同學們不僅發現了軸對稱圖形的這個特點，而且在這個過程中還掌握了一種科學嚴謹的數學研究方法。接下來，我們就用軸對稱圖形的這個特點來解決一個實際問題。（課件出示例2。）想象一下，完整的這個圖形應該是什么樣呢？

生：是個五角星。

師：你能把這個軸對稱圖形補全嗎？大家動手試一試。（生展示交流。）

師：你們怎么畫得又快又好？

生：我是先畫出這些點的對稱點，最后把它們連起來。

師：你們在畫的時候，其實都是先找到這幾個點，為什么就單單找了幾個對應點呢？

生：這些對應點都在端點，找準了，就可以畫得又快又準了。

師：對呀，它們是這個圖形的關鍵點。找到關鍵點，定準了它們的對應點，最后就可以連點成形了。（板書：找關鍵點——定對稱點——連點成形。）

四、靈活應用，拓展延伸

師：通過動手實踐，你們歸納出了補全軸對稱圖形的好方法，下面就應用這個好方法，我們再來畫一畫。（學生完成數學書P84做一做2，展示交流畫法。）

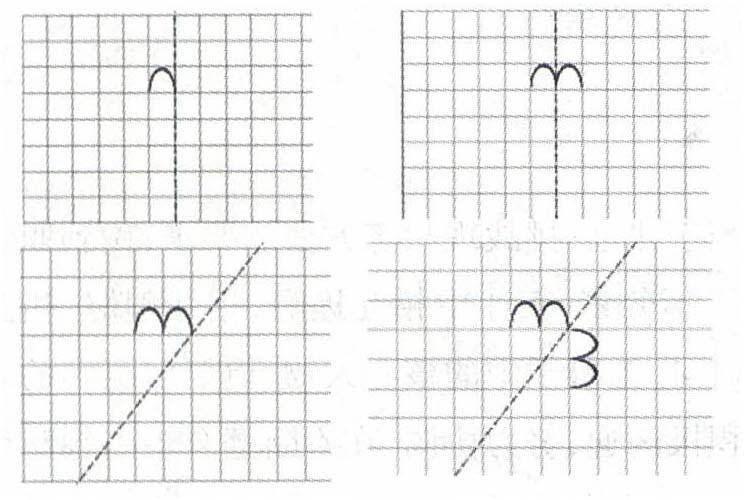
師：看來，同學們已經掌握了補全軸對稱圖形的方法。下面給你們來一個挑戰，你能畫出這條弧線的對稱圖形嗎？

生：能。

師：誰到前面指一指？（生指畫。）

師：看，是這樣嗎？（課件出示。）再看，我們換一條對稱軸，它們兩個的對稱圖形在哪兒呢？（生指畫。）

師：對嗎？再變，它的對稱圖形在哪兒呢？你來指一指，注意看他的手勢。（生指畫。）

師：老師把它進行了裝飾。

師：正是因為生活中有很多的軸對稱現象，才將我們的生活裝扮得更加美麗，老師就把這些花朵送給你們，希望你們就像美麗的鮮花一樣在陽光下茁壯成長。

評析：

張老師的這節課依托學生的認知經驗，以精巧的數學活動為載體，促進了學生對軸對稱圖形的性質、特征及其應用的自主建構，體現了學生的數學學習過程是生動的、主動的、富有個性的過程。在學生去經歷、去發現、去再創造的活動過程中，教師因學活教，順學而導，突出了對學生空間觀念這一數學核心素養的培養。

一、關注已有經驗，在喚醒中發展空間觀念

這節“軸對稱”是教材改版后新增的教學內容，是二年級學習的簡單軸對稱知識的延伸。張老師充分挖掘教材資源，通過課前挑戰哈佛大學的測試題，喚醒學生對學習過的軸對稱圖形的認知，激發學生的學習興趣。教師深知數學概念的掌握要建立在生活經驗和認知經驗的基礎上。教師借助學生的生活經驗，通過觀察、書空畫軸感知生活中的對稱現象，而后舍棄各個實物圖中非幾何屬性的因素，抽象出平面圖形，進而完成畫對稱軸的自主學習，這樣的設計能體現將生活經驗提煉為數學概念的過程，突出本節課研究的對象是圖形，在激活經驗中發展了學生的空間觀念。

二、關注探究體驗。在建構中發展空間觀念

為了深化學生對軸對稱圖形特征的認識和理解，教師設計了折一折、找一找、畫一畫、連一連等層層深入的探究體驗活動，使學生經歷“感知對稱——探究對稱——理解對稱”的過程，知識建構層層深入。教師教學重點找得準、落得實，策略有效。例1的教學是本節課的重點。教師引導學生在“怎樣判斷一個圖形是否是軸對稱圖形”問題的思考下，自主進行方法的遷移，利用對折，發現點重合，引出對稱點的教學。再讓學生從圖中尋找到更多組對稱點，學生在多維的找對稱點的方法的碰撞交流中，感知對稱點的連線與對稱軸互相垂直，在明晰對稱點到對稱軸距離概念的基礎上，探究得到“對稱點到對稱軸距離相等”這一重要性質特征，并進行了有效升華。教師引導學生進一步探究發現，對稱圖形上每一個點都可以找到它的對應點，這些點的連線是對稱線段，由對稱線段圍成的圖形是對稱圖形。這樣由點到線、到形，層層深入，加深學生對于軸對稱圖形特點的認識，并且利用在頭腦中想象圖形沿著對稱軸對折，兩部分完全重合的過程，培養了學生空間距離感和方位感，以此提升學生的空間觀念。

三、關注遷移拓展，在應用中發展空間觀念

軸對稱是“圖形與幾何”領域中圖形與轉換中的重要內容，發展學生的空間觀念也是本節課的一個重要目標。張老師不僅在新知的建構中發展學生的空間觀念，更注重學生在知識的遷移和應用中發展空間觀念。首先，教師在補全對稱圖形的知識應用中發展了學生的空間觀念，抓住關鍵對應點進行畫法的優化。其次，借助做一做中的基礎題目，有效地落實了知識目標。最后，教師進行了思維層次更高的空間想象能力的引領和培養。教師引導學生一邊想象，一邊書空畫出一段弧線的以豎直方向為對稱軸的軸對稱圖形，一組弧線，兩組弧線以左、右傾斜45°不同方向為對稱軸的軸對稱圖形，最終形成了美麗的花朵，引發學生對對稱美的關注和感知，把對學生空間觀念素養的培養推向高潮。前一次任務的順利完成恰恰是下一次挑戰性任務的開始，使學生的空間觀念在不斷的思維挑戰中得到發展和升華。

編輯/宋宇