多操縱面交叉耦合的SQP控制分配策略

易　堅,陳　勇,董新民,支健輝,程建鋒

(1.空軍工程大學航空航天工程學院,陜西 西安 710038;2.空軍西安飛行學院,陜西 西安 710301)

?

多操縱面交叉耦合的SQP控制分配策略

易堅1,陳勇1,董新民1,支健輝1,程建鋒2

(1.空軍工程大學航空航天工程學院,陜西 西安 710038;2.空軍西安飛行學院,陜西 西安 710301)

針對多操縱面飛機交叉耦合效應下易產生虛擬控制誤差和舵效中和等問題,提出了一種基于改進序列二次規劃的控制分配策略。以操縱面偏量為參數構建優化目標,基于舵效線性假設分別研究了基于線性規劃和二次規劃的多操縱面線性控制分配方法。進一步考慮非線性交叉耦合效應,分別建立了序列線性和序列二次規劃的交叉耦合控制分配模型,并設計了改進的Hessian矩陣,以實現序列二次規劃的優化求解。仿真表明,基于改進序列二次規劃的控制分配策略能夠合理地利用所有交叉耦合操縱面實現非線性分配,優于線性規劃、二次規劃和序列線性規劃控制分配方法。

多操縱面飛機; 控制分配; 交叉耦合; 序列二次規劃

0　引　言

為保證復雜條件下的可控性、隱身性和安全性等性能,現代飛行器突破常規操縱面布局形式,在機翼上布置多組操縱面,如美國的B-2、X-47B等。操縱面數量的增多,既保證了飛控系統控制冗余度、提高操縱指令可行性,也導致操縱面布置密集,操縱面間氣動干擾增強,交叉耦合效應明顯[1-5],操縱面控制效能呈強烈的耦合非線性。為此,考慮舵效交叉耦合非線性,將虛擬控制指令精確合理地分配到各操縱面,對于實現多操縱面飛機有效控制具有十分重要的意義。

控制分配技術是實現多操縱面指令分配[6-8]的有效途徑,且在汽車[9]、艦船[10]等控制領域也得到了廣泛的運用。基于舵效線性假設,國內外專家提出了直接分配[11-12]、加權偽逆[13]及動態控制分配[14]等方法。顯然,上述方法均未考慮舵效非線性,在交叉耦合影響下將存在較大偏差,為虛擬控制指令的有效分配帶來了難題。

為此,國內外專家對舵效非線性下的控制分配問題展開了深入研究。文獻[15]采用非線性曲線擬合力矩控制效能,基于序列二次規劃(sequential quadratic programming,SQP)提出了一種非線性控制分配方法;文獻[16]針對飛機左右對稱操縱面,提出一種非線性力矩可達集的構建方法,結合非線性規劃對虛擬控制指令進行了直接分配;文獻[17]通過將控制效能分段線性化,將非線性控制分配問題轉換為分段線性控制分配問題,并結合混合線性規劃進行了虛擬控制指令地有效求解。文獻[3]考慮X-33型航天器矢量發動機推力與推矢偏角對三軸力矩的交叉耦合作用,將交叉耦合控制分配問題轉化為序列線性規劃問題;文獻[4]進一步用于解決F-18飛機前緣襟翼與副翼間耦合力矩效應下的控制分配問題,取得了較好的指令分配結果。文獻[5]針對某飛翼飛機開裂式方向舵與相鄰升降副翼之間的交叉耦合氣動效能,采用線性操縱面來補償交叉耦合操縱面控制力矩,能夠獲得次優的操縱面組合,具有較好的實時性。

本文針對交叉耦合效應下線性控制分配誤差大、易出現舵效中和的問題,進一步考慮多操縱面飛機的交叉耦合效應,提出一種基于改進序列二次規劃的控制分配策略。在對比研究線性與非線性控制分配方法的基礎上,建立了交叉耦合下的非線性控制分配優化模型,推導了基于改進序列二次規劃的求解方法,實現了虛擬控制指令到操縱面的合理精確分配,同時避免不必要的舵效中和。通過仿真驗證了方法的有效性。

1　多操縱面線性控制分配

對于多操縱面飛機,合理分配操縱面指令以實現期望虛擬控制指令的過程,就是控制分配。常用的虛擬控制指令有:飛機三軸角加速度、三軸控制力矩、力系數等,記為v∈Rn。忽略多操縱面飛機執行器動態,控制分配方程可描述為

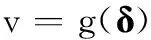
(1)

式中,δ∈Rm為操縱面偏轉量,滿足m>n;g:Rm→Rn表示操縱面偏轉量δ到虛擬控制指令v的映射函數。

在小擾動條件下,多操縱面飛機的虛擬控制指令與操縱面偏轉量可近似為線性關系,根據泰勒定理,可以得到線性控制分配方程[1,11]為

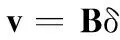
(2)

式中,B∈Rn×m為控制效率矩陣。

由于結構、載荷等方面的約束,操縱面偏轉受到物理限制,可描述為

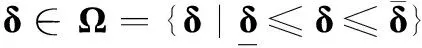
(3)

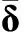
在諸多控制分配方法中,常選擇操縱面與參考位置偏離量最小為目標函數,建立線性控制分配優化模型,實現控制面阻力最小、隱身性能最好等特征要求。根據評價指標的不同選取,線性控制分配可分為線性規劃控制分配法(linear programming-based control allocation,LPCA)和二次規劃控制分配法(quadratic programming-based control allocation,QPCA)。

1.1線性規劃控制分配方法

嚴格以操縱面偏離參考位置的l1范數為評價指標,建立線性規劃控制分配模型:

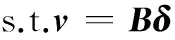
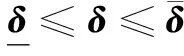
(4)

式中,δp∈Rm為理想操縱面位置;W∈Rm×m為對角矩陣,表示操縱面偏轉控制權值。引入松弛因子δs∈Rm,線性控制分配模型式(4)可轉化為

(5)

式中,w1,w2,…,wm為W矩陣的對角元素。

可用單純形法對式(5)進行求解。

1.2二次規劃控制分配方法

考慮以操縱面偏離參考位置的l2范數為評價指標,建立二次規劃控制分配模型:

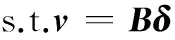
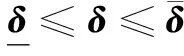
(6)

將模型式(6)的優化目標函數J展開,可得

(7)

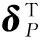
(8)

則控制分配模型式(6)等價為

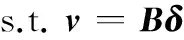
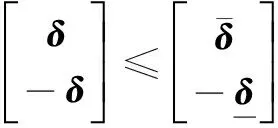
(9)

可用有效集法對式(9)進行求解。

2　多操縱面交叉耦合控制分配

對于多操縱面飛機而言,操縱面間常存在較強的非線性交叉耦合效應,采用線性控制分配方法進行指令分配不可避免地具有局限性。因此,為實現虛擬控制指令到操縱面的合理有效分配,必須在控制分配模型中考慮交叉耦合效應。

多操縱面飛機虛擬控制指令v=[vlvmvn]T與操縱面偏轉量δ的非線性映射可擬合成多項式形式。此時,操縱面間的交叉耦合效應具有如下的雙線性形式[3]:

(10)

式中,δi和δj分別表示操縱面i、j的偏轉量;Δvr(δi,δj)表示操縱面δi和δj組合偏轉的交叉耦合效能對虛擬控制指令分量vr的影響。當i=j時,式(10)表征操縱面δi的二階非線性控制效能,此時可視為操縱面自身的交叉耦合影響。

結合式(10),可將含操縱面交叉耦合效應的非線性控制分配方程表示為

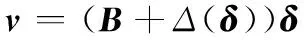
(11)

式中,Δ(δ)為操縱面交叉耦合控制效能陣,即

(12)

式中,Ql、Qm和Qn分別表示虛擬控制指令三軸交叉耦合系數矩陣,可描述為

(13)

式中,Qr表示虛擬控制分量vr的交叉耦合系數矩陣。

控制分配方程式(11)考慮了操縱面的交叉耦合效應,是求解非線性交叉耦合控制分配問題的基礎。針對該問題,常采用序列求解最優控制分配模型的方法進行求解[3-5]。根據不同的評價指標,本文基于交叉耦合操縱面研究了序列線性規劃控制分配方法(sequential linear programming-based control allocation,SLPCA),并提出一種序列二次規劃控制分配方法(sequential quadratic programming-based control allocation,SQPCA)。

2.1序列線性規劃控制分配方法

序列線性規劃控制分配方法[3]的基本思想是將考慮交叉耦合效應的控制分配問題描述為非線性約束優化問題,在求解一系列子線性規劃的基礎上逐步逼近原控制分配問題的最優解。

采用操縱面偏離參考位置的l1范數為評價指標,建立交叉耦合非線性控制分配模型為

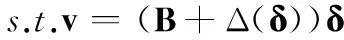
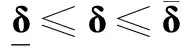
(14)

為求解模型式(14),引入松弛因子δs∈Rm,基于序列線性規劃設計控制分配求解模型為

(15)

式中,δk為第k步計算得到的操縱面偏轉量。

收斂條件通常為達到最大計算時間或滿足

(16)

式中,ε表示容許誤差。

2.2序列二次規劃控制分配方法

研究表明[12,18-19],采用操縱面偏離參考位置的l1范數作為優化指標,控制分配結果可能只有部分操縱面被使用,易造成舵效中和與操縱面飽和等現象,無法發揮所有操縱面的綜合控制效能。為綜合利用所有操縱面實現協調偏轉,本文提出一種基于改進序列二次規劃來研究操縱面交叉耦合的非線性控制分配方法。

采用操縱面偏離參考位置的l2范數為評價指標,建立交叉耦合非線性控制分配模型為

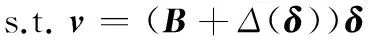
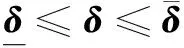
(17)

將式(17)中的優化目標函數J展開,忽略常數項,并令

(18)

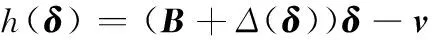
(19)

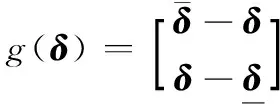
(20)

則控制分配模型式(17)可等價為優化模型:

min f(δ)

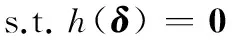
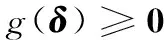
(21)

為求解模型式(21),不妨定義拉格朗日函數:

(22)

式中,μ∈Rn、λ∈R2m為對應約束的拉格朗日乘子向量。模型(21)的Kuhn-Tucker條件為

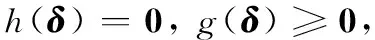
(23)

采用Newton法求解式(23),得到迭代解為

(24)

(25)

式中,上標“?”表示Moore-Penrose逆;dk為Newton梯度下降方向,是如下二次規劃子問題的最優解:

(26)

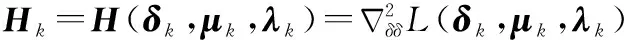
根據關系式(24)～式(26),可得到序列二次規劃控制分配方法的迭代解為

(27)

式中,αk為步長因子。截止條件為

(28)

式中,g(δk)-=max{0,-g(δk)};ε1、ε2為容許誤差。

(1)罰參數σk的選擇

為保證f(δ)最優的同時h(δ)和g(δ)滿足約束條件,應該選擇下降方向dk使得如下價值函數收斂:

(29)

式中,罰參數σ>0;g(δ)-=max{0,-g(δ)}。

已經證明[20],若選擇ζ>0,且

(30)

則dk同時是φ(δ)在δk處的下降方向。

(2)步長因子αk的選擇

基于價值函數式(29),采用Armijo搜索法選擇步長因子。給定β∈(0,1),τ∈(0,0.5),取步長因子αk=βz。其中z為滿足下列不等式的最小非負整數:

(31)

(3)近似Hessian陣Θk的選擇

在序列求解最優值的過程中,Hessian陣Hk的計算量較大,直接影響算法的實時性。為此,本文基于擬牛頓法,采用修正的BFGS算法求解近似Hessian陣Θk,以實現對Hk陣的有效逼近。

為保證Hessian陣正定,選擇Θk迭代解為

(32)

式中

(4)計算步驟

針對交叉耦合控制分配模型式(17),基于改進序列二次規劃法進行求解,計算步驟如下:

步驟1初始化:令k=0,針對控制分配模型式(17),給定初始點(δ0,μ0,λ0)、Θ0=I,設定容許誤差0<ε1,ε2?1。

步驟2計算下降方向:求解二次規劃問題

(33)

得到δk處的下降方向dk。

步驟3判斷收斂性:若‖dk‖1≤ε1且‖h(δk)‖1+‖g(δk)-‖1≤ε2,滿足容許誤差,終止計算,得到交叉耦合控制分配優化解δk。否則轉步驟4。

步驟4計算下降步長:利用式(30)確定罰函數σk,并利用式(31)確定步長因子αk,進而得到下降步長αkdk。轉步驟5。

步驟5更新迭代點:令δk+1=δk+αkdk,按式(25)計算拉格朗日乘子向量μk+1、λk+1,轉步驟6。

步驟6校正Hessian矩陣:利用式(32)計算近似Hessian陣Θk+1。轉步驟7。

步驟7令k=k+1,轉步驟2。

3　仿真與分析

3.1仿真模型

為驗證本文控制分配策略的有效性,采用F-18飛機[2]進行對比仿真。該飛機共有7組獨立操縱面,記為δ=[δle,δre,δla,δra,δr,δtef,δlef]T,其中δle、δre表示左、右升降舵,δla、δra表示左、右副翼,δr表示方向舵,δtef和δlef表示后緣和前緣襟翼。各操縱面偏轉約束如表1所示。

表1　操縱面偏轉位置上下限

在馬赫數0.3,攻角15°,側滑角0°,高度10 000英尺的飛行條件下,選擇滾轉、俯仰以及偏航力矩系數Cl、Cm以及Cn為虛擬控制指令,由文獻[2]可得到操縱面偏轉量到虛擬控制指令的非線性映射。以橫向滾轉通道為例,可描述為

(34)

其余通道數據可參考文獻[2]。可以看出,F-18飛機前緣襟翼δlef與左右副翼δla、δra間的非線性交叉耦合效應明顯。

進一步計算可知線性化控制效率矩陣為

虛擬控制指令分量的交叉耦合系數矩陣為

為驗證本文控制分配策略的有效性,對以下4種方案進行對比研究:

(1)LPCA方案:不考慮操縱面間交叉耦合非線性,基于線性規劃求解控制分配模型式(4);

(2)QPCA方案:不考慮交叉耦合非線性,基于二次規劃求解控制分配模型式(6);

(3)SLPCA方案:考慮交叉耦合非線性,基于序列線性規劃求解控制分配模型式(14);

(4)SQPCA方案:考慮交叉耦合非線性,基于改進序列二次規劃求解模型式(17)。

3.2性能比較

給定期望虛擬控制指令,圖1所示為4種方案生成的虛擬控制指令動態曲線。可以看出,LPCA方案和QPCA方案未考慮操縱面之間的非線性交叉耦合影響,產生了較大的虛擬控制偏差。而SLPCA方案和SQPCA方案有效考慮了操縱面交叉耦合非線性對控制分配結果的影響,實現了對期望虛擬控制指令的有效分配。

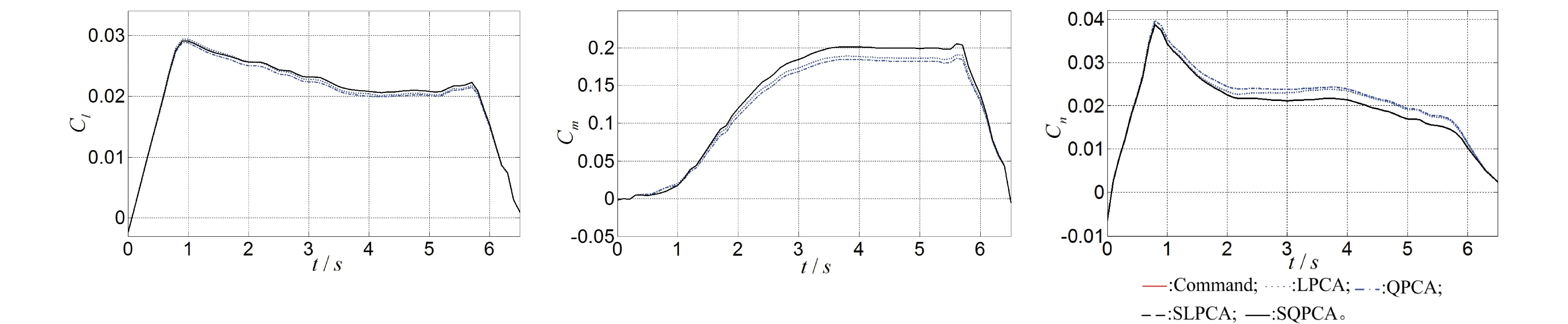
圖1　虛擬控制指令的動態曲線Fig.1　Dynamic profile of the virtual control command

圖2所示為4種控制分配方案生成的操縱面偏轉指令曲線。對比結果可以看出,LPCA方案與SLPCA方案產生的操縱面偏轉過程基本一致,但存在未考慮操縱面交叉耦合產生的控制偏差。同樣地,QPCA方案與SQPCA方案亦有類似的結果。正是這種偏差的存在,導致了圖1中的跟蹤誤差。

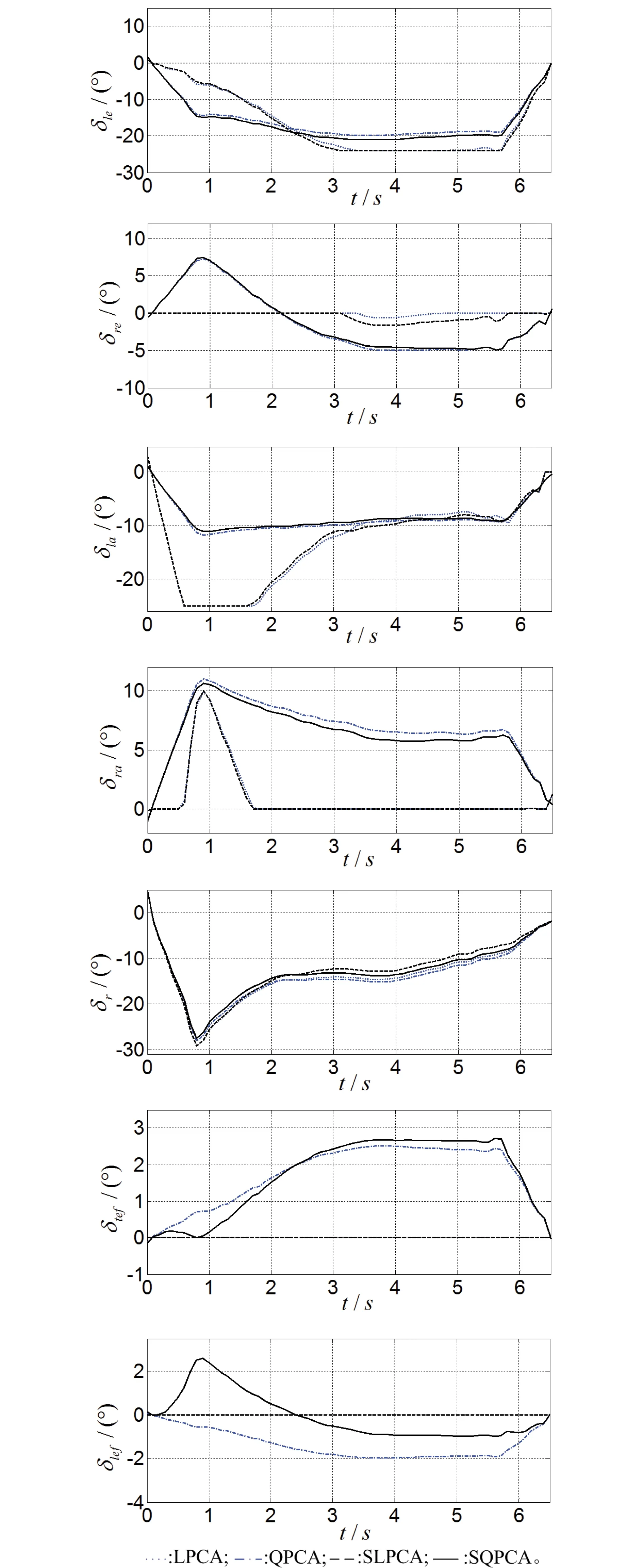
圖2　操縱面偏轉指令曲線Fig.2　Deflection command of the control surfaces

值得注意的是,圖2中LPCA方案與SLPCA方案左副翼分別在第3.1～5.7 s、第3.4～4.7 s時達到飽和,在0.6～1.6 s左升降舵也同時飽和。而通過QPCA方案與SQPCA方案的操縱面偏轉指令可知,這種飽和是可以通過所有操縱面的協調偏轉來避免的,LPCA方案和SLPCA方案則表現出一定的舵效中和。另外,LPCA方案與SLPCA方案幾乎未使用前、后緣襟翼,且在0～3.1 s內未使用右升降舵、在0～0.5 s和1.7～6.4 s時未使用右副翼。不利于所有操縱面控制效能的綜合發揮,而QPCA方案與SQPCA方案則可利用所有操縱面實現協調偏轉。

考慮到SLPCA方案和SQPCA方案需進行迭代計算,現將計算結果與LPCA方案和QPCA方案進行對比,以分析控制分配性能。考慮單次指令計算時間及其分配誤差,結果如表2所示。

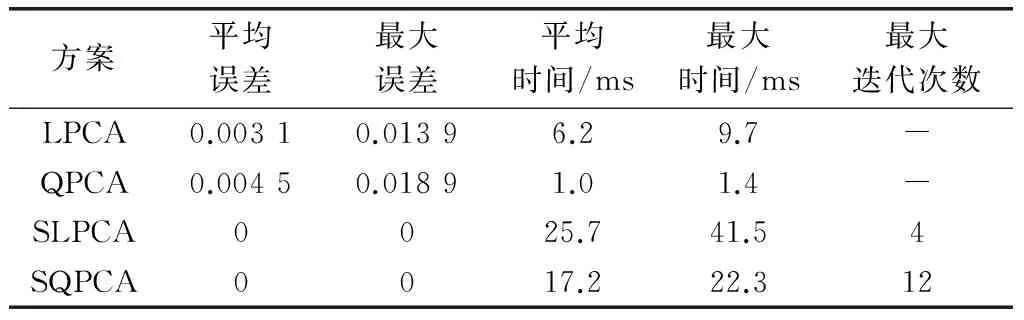
表2　各控制分配方案性能對比

可以看出,對于給定的虛擬控制指令,LPCA和QPCA方案均產生了一定的虛擬控制偏差,最大值達到了0.018 9。而SLPCA和SQPCA方案能夠實現有效的準確分配,基本無控制誤差。但是由于需進行迭代計算,SLPCA和SQPCA方案均耗時較多。其中SQPCA雖然迭代次數更多,但相對SLPCA而言具有較好的實時性。

可見,SQPCA方案能夠有效考慮操縱面間交叉耦合非線性,精確無誤差地分配虛擬控制指令,避免舵效中和,實現所有操縱面的合理協調偏轉。

4　結　論

針對多操縱面飛機交叉耦合非線性情形下的控制分配問題,本文對比研究了線性與非線性控制分配方法,引入罰函數和步長因子改進序列二次規劃,提出了一種交叉耦合非線性情形下的控制分配策略。結合F-18多操縱面飛機模型對比仿真表明:

(1)與線性控制分配法相比,該方法可考慮操縱面交叉耦合非線性,實現虛擬控制指令無誤差精確分配;

(2)與序列線性規劃控制分配法相比,該方法可綜合控制效能分配操縱面指令,實現操縱面協調偏轉,避免舵效中和。

值得注意的是,提出的交叉耦合非線性控制分配策略可適用于汽車、導彈、艦船等過驅動控制系統,具有良好的普適性。

[1] Johansen T A,Fossen T I.Control allocation-a survey[J].Automatic,2013,49(5):1087-1103.

[2] Bordignon K A.Constrained control allocation for systems with redundant control effectors[D].Virginia:Virginia Polytechnic Institute and State University,1996.

[3] Oppenheimer M W,Doman D B.A method for including control effector interactions in the control allocation problem[C]//Proc.of the AIAA Guidance,Navigation and Control Conference and Exhibit,2007:1-10.

[4] Ma J J.Research and application of control allocation theory for overactuated systems[D].Changsha:National University of Defense Technology,2009.(馬建軍.過驅動系統控制分配理論及其應用[D].長沙:國防科學技術大學,2009.)

[5] Xu M X,Zhu X P,Zhou Z,et al.A control allocation method for flying wing aircraft with control effector interactions considered[J].Journal of Northwestern Polytechnical University,2014,32(1):69-73.(徐明興,祝小平,周洲,等.一種考慮交叉耦合效應的飛翼布局飛機控制分配方法[J].西北工業大學學報,2014,32(1):69-73.)

[6] Kishorea A W C,Dasgupta S,Ray G,et al.Control allocation for an over-actuated satellite launch vehicle[J].Aerospace Science and Technology,2013,28(1):56-71.

[7] Hamayun M T,Edwards C,Alwi H.A fault tolerant control allocation scheme with output integral sliding modes[J].Automatica,2013,49(6):1830-1837.

[8] Cui L,Yang Y.Disturbance rejection and robust least-squares control allocation in flight control system[J].Journal of Guidance Control and Dynamics,2011,34(6):1632-1643.

[9] Tj?nn?s J,Johansen T A.Stabilization of automotive vehicles using active steering and adaptive brake control allocation[J].IEEE Trans.on Control Systems Technology,2010,18(3):545-558.

[10] Scibilia F,Skjetne R.Constrained control allocation for vessels with azimuth thrusters[C]//Proc.of the Manoeuvring and Control of Marine Craft,2012:7-12.

[11] Durham W C.Constrained control allocation:three moment problem[J].Journal of Guidance,Control,and Dynamics,1994,17(2):330-336.

[12] Bodson M.Evaluation of optimization methods for control allocation[J].Journal of Guidance Control and Dynamics,2002,25(4):703-711.

[13] Chen Y,Dong X M,Xue J P,et al.Multi-objective optimization design of weight coefficients for weighted control allocation scheme[J].Control and Decision,2013,28(7):991-1001.(陳勇,董新民,薛建平,等.賦權控制分配策略的權系數多目標優化設計[J].控制與決策,2013,28(7):991-1001.)

[14] Luo Y,Serrani A,Yurkovich S,et al.Model-predictive dynamic control allocation scheme for reentry vehicles[J].Journal of Guidance Control and Dynamics,2007,30(1):99-113.

[15] Poonamallee V L,Yurkovich S,Serrani A.A nonlinear programming approach for control allocation[C]//Proc.of the American Control Conference,2004:1689-1694.

[16] Bolender M A,Doman D B.Method for determination of nonlinear attainable moment sets[J].Journal of Guidance Control and Dynamics,2004,27(5):907-914.

[17] Bolender M A,Doman D B.Nonlinear control allocation using piecewise linear functions[J].Journal of Guidance Control and Dynamics,2004,27(6):1017-1027.

[18] Bodson M,Frost S A.Control allocation with load balancing[J].Journal of Guidance Control and Dynamics,2011,34:380-387.

[19] Frost S A,Bodson M.Resource balancing control allocation[C]//Proc.of the American Control Conference,2010:1326-1331.

[20] Rao S S.Engineering optimization theory and practice[M].Canada:Wiley,2009.

SQP-based control allocation for multiple effectors with interactions

YI Jian1,CHEN Yong1,DONG Xin-min1,ZHI Jian-hui1,CHENG Jian-feng2

(1.College of Aeronautics and Astronautics Engineering,Air Force Engineering University,Xi’an 710038,China; 2.The Air Force Xi’an Flight Academy,Xi’an 710301,China)

To deal with the problem of virtual control error and control efficiency counteracts under interactions for multiple effectors aircraft,a modified sequential quadratic programming (SQP)-based control allocation scheme is proposed.By taking the parameters of control deflections as the optimization objective,the linear programming and quadratic programming-based linear control allocation methods are researched respectively based on the assumption of linear control efficiencies.Furthermore,by considering the nonlinear interactions,the sequential linear programming and SQP-based control allocation models are built.A modified Hessian matrix is designed and applied to solve the SQP problem optimally.Simulation results show that the modified SQP-based control allocation scheme can utilize all the interactional control effectors reasonably to achieve the nonlinear allocation,which is better than the linear programming,quadratic programming and sequential linear programming control allocation.

multiple effectors aircraft; control allocation; interactions; sequential quadratic programming (SQP)

2015-09-25；

2016-07-25；網絡優先出版日期：2016-08-25。

國家自然科學基金(61304120,61473307)；航空科學基金(20155896026)資助課題

V 249.1

ADOI:10.3969/j.issn.1001-506X.2016.11.24

易堅(1992-),男,博士研究生,主要研究方向為多操縱面飛行器控制分配。

E-mail:1361475660@qq.com

陳勇(1984-),男,講師,博士,主要研究方向為飛行控制、控制分配、容錯控制。

E-mail:cheny_043@163.com

董新民(1963-),男,教授,博士研究生導師,主要研究方向為飛行器控制理論及應用。

E-mail:dongxinmin@163.com

支健輝(1989-),男,博士研究生,主要研究方向為多操縱面飛行器容錯控制理論及應用。

E-mail:zhijianhui2012@163.com

程建鋒(1984-),男,工程師,博士,主要研究方向為飛行器導航制導與控制。

E-mail:chengjianfeng2008@163.com

網絡優先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160825.1438.002.html