五年級和六年級學生分數表征轉化能力的調查研究

郭 萌，熊妍茜，楊新榮，陳朝東

?

五年級和六年級學生分數表征轉化能力的調查研究

郭 萌1，熊妍茜1，楊新榮1，陳朝東2

（1．西南大學數學與統計學院，重慶 400715；2．四川大學數學學院，四川成都 610000）

分數表征是分數概念學習的一部分，也是概念理解的重要方法．分數表征包括面積表征、集合表征、數軸表征和符號表征等，這4類表征及其轉化與分數概念理解緊密相連，對分數教學具有重要意義．通過改編Kurt和Cakiroglu的分數表征轉化測試工具，研究者調查了247名5年級學生和264名6年級學生的分數表征轉化能力．調查發現小學生在數軸表征和假分數表征相關轉化問題上表現較差，不能很好地理解面積（集合）表征與數軸表征的區別．此外六年級學生數軸表征轉化能力較五年級有顯著提升．建議教師應該重視分數多元表征的教學尤其是數軸表征和假分數表征的教學，通過分數表征轉化任務幫助學生建立起全面的分數表征系統和知識結構，促進學生分數概念的發展．

分數表征；分數表征轉化；分數概念；數軸；小學生

1 引 言

當前國際數學課程改革的一個重要特點在于培養學生多元數學表征能力．如在美國教師協會頒布的《學校數學課程標準和原則（2000）》中就明確將表征作為過程標準之一．通過數學學習，學生要能：（1）創建和使用表征組織、記錄和交流數學思想；（2）選擇、運用和轉化各種數學表征來解決問題；（3）使用表征來解讀物質的、社會的、和數學現象[1]．《義務教育數學課程標準（2011）》[2]也指出課程內容的呈現應該注意多樣性，以豐富學生的數學學習經驗．然而要培養學生多元數學表征能力，不僅要求在數學教材編寫中用多種形式呈現數學概念，更要求在數學課堂教學中給學生提供使用多種表征的機會．

在數學領域，表征主要包括：（1）內部表征．如有關數學活動的抽象或者學習者通過自身經歷所形成的認知圖示；（2）外部表征．如數字、代數方程、圖象、表格、圖表等有關數學概念的外在表示[3]．而對于一個抽象的數學概念而言，其都可以通過多種外部表征予以表達，如圖象、符號、語言等．不過由于數學自身的復雜性和抽象性，單一外在表征難以充分揭示數學本質，由此學生需要借助多元外部表征從多元具體形式中抽象知識或問題的內在結構[4]．真正理解一個數學概念不僅需要學生能在多種本質各異的表征中辨別相關的數學概念，更要求學生能靈活自如地在各種不同表達中進行轉化[5]．此外，在解題過程中，借助一個好的形象表征學生可以形成一個有效的抽象表征，從而更好地了解問題解決的實質和關鍵，然后再借助形象表征的各種方式達到對問題的解決[6]．由此可見，表征轉化能力在數學概念理解和問題解決中有著不可替代的作用．然而，現實中，老師和學生卻常常忽視多元表征轉化能力的培養和訓練．教師所教的和學生所學的數學內容通常在單一的表征系統中就已結束，而沒有在不同的表征之間建立起應有的聯系[1]．貝洱認為表征系統是互動的而不是線性的，同一表征內部的轉化以及不同表征方式之間的轉化有利于學生知識理解，應該像單個表征的學習一樣受到重視[7~8]．

分數概念是學生在中學前所遇到的最困難，同時也是最重要的數學知識之一[9]．其困難的根源在于分數概念的多重結構，其包括部分整體、測量、商、算子、比五種子概念[10]．同時分數也有多種外部表征，如符號表征、圖形表征、語言表征、實物表征、現實情景表征等．過去關于分數教與學的研究中，國內研究者主要關注于學生分數概念的掌握和分數表征的使用．如倪玉菁調查了深圳五、六年級小學生對分數意義和性質的學習，測試卷涉及面積表征、線段表征、集合表征和數線表征[11]．該研究發現學生在測量概念和等值分數的理解上存在困難．此外，張睆和辛自強研究了分數概念的個體建構機制[12]．多數研究聚焦于多種分數概念的認知和教學，學生分數表征轉化能力的研究在國內很少受到關注．然而，分數表征轉化能力對學生分數的學習非常重要．在學習分數概念時，學生需要經歷從分月餅到分圓形，再到抽象出分數符號的過程，這本質上是實物表征到圖形表征，再到符號表征的轉化．各種表征間的轉化過程連同3種分數表征方式一方面可以幫助學生從直觀到抽象地理解分數概念．但同時，各種表征抽象復雜程度上的差異也將造成學生對分數概念理解和轉化上的困難．分數表征轉化對學生分數學習和思維發展有至關重要的作用，卻未受到教師和研究者的重視．基于此，研究主要探討五、六年級學生分數表征轉化能力現狀和存在的問題（主要涉及：符號表征、面積表征、集合表征、數軸表征），以期為數學教學和教材編寫提供更為直接的建議．

2 研究方法

2.1 研究對象

參與研究的511名學生選自重慶3所背景各異的小學．其中247名五年級學生和264名六年級學生，其中男生269人，女生242人（具體信息見表1）．3所學校使用的教科書都是西南師范大學版小學數學教材．根據教材知識編排，小學生在五年級下學期已完成分數的意義、真分數與假分數、分數的基本性質、分數的加減法等內容的學習，接觸過研究所涉及的4種分數表征方式．

表1 被試學生基本情況

2.2 研究工具

研究主要采用測試法，以Kurt和Cakiroglu的分數表征轉化測試卷[13]為基礎，根據中國數學教學情況和教材使用情況對測試工具進行修改與調整．測試工具包括4種分數表征方式即符號表征、數軸表征、面積表征、集合表征．其中數軸表示分數“測量”的概念，面積和集合表示分數“部分整體”概念．測試卷共設置12道題目涵蓋任意兩種表征之間的轉化，每道題目預先給出一種分數表征方式，要求學生將其轉化為規定的表征方式，并寫出自己的思考過程．整個測試卷的Cronbach’s Alpha系數為0.663，表明其內部一致性較好．測試卷樣題如圖1所示．

圖1 分數表征轉化測試卷樣題

2.3 數據分析

數據分析按如下3步完成．首先對于學生回答進行記分．每題答對記1分，答錯記0分．所有學生回答由第一作者判分，第二作者檢查了所有判分情況且與第一作者討論了不同意見部分．此后對測試卷結構做了因子分析，提煉出了3個因子．最后針對這3個因子，就學生性別和年級進行了差異檢驗．

3 研究結果

3.1 測試卷結構

為分析測試卷的結構同時了解中國學生分數表征能力結構，對測試卷所得數據進行了因子分析．Bartlett球形檢驗卡方值統計顯著，因此可認為相關矩陣與單位陣有顯著差異．同時，KMO值為0.75，根據Kaiser給出的KMO度量標準可知原變量適合做因子分析．因子中特征根大于1的共有3個，3個因子分別解釋測試卷的29.73%、17.60%、15.16%，方差累計貢獻率有62.48%，可解釋12道轉化題目多于一半的信息，故提取3個主成分．

表2為使用Varimax最大方差法旋轉旋后的因子載荷矩陣．第一個因子包含題項有T1、T5、T6、T8、T11、T4，這些題目都與數軸相關，命名為“數軸相關表征轉化”．第二個因子包含題項有T2、T9、T7，題目至少涉及面積表征和集合表征其中之一，且不涉及假分數，命名為“面積和集合表征轉化—真分數”．第三個因子包含有題項T12、T10、T3，題目至少包含面積表征和集合表征其中之一，且都涉及假分數，故命名為“面積和集合表征轉化—假分數”．3個主成分將12道測試題分為3個部分，分類標準為是否涉及數軸和假分數．按照原測試卷的設計和中國學生的情況將測試卷題目作如表3所示劃分．

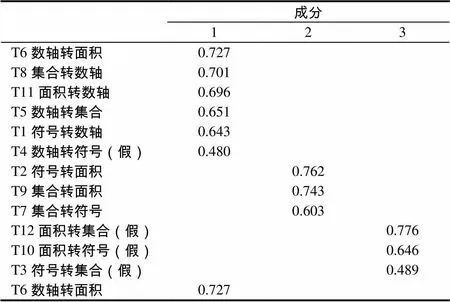
表2 旋轉后的因子載荷矩陣

表3 題目分類表

注：“T2符號轉面積”：T2為符號表征轉化為面積表征的題目；“T12面積轉集合（假）”：T12為面積表征轉化為集合表征的題目，且其涉及假分數

3.2 五六年級小學生分數表征轉化能力基本情況

學生在各個題目上的表現列于圖2．總的來說，學生在分數表征轉化問題上表現一般，其平均正確率為71.59%，不同題目上的表現有較大差異．測試結果的平均數和標準差按3個維度列于表4，從表中可以看出平均正確率

面積與集合真分數>面積與集合假分數>數軸，

也就是說面積與集合表征相關轉化題目上的表現優于數軸的表征轉化．此外，涉及假分數表征的題目上學生也表現出一定的困難．

具體而言，學生在與面積表征轉化和集合表征轉化相關的題目上表現最好．“面積和集合表征轉化—真分數”的平均正確率達97.20%，且學生個體之間表現較為穩定（標準差為0.12）．從圖2可以看出“面積和集合表征轉化——真分數”相關題目T2、T8、T7正確率都在96%以上，其中T7的正確率最高達98%．其次，學生在假分數表征上表現出一定的問題．相關題目T12、T3、T10正確率均穩定在80%左右．在與面積和集合表征相關的題目中，學生在真分數表征轉化題目上平均正確率比假分數高近17個百分點．

值得指出的是，涉及數軸表征的相關轉化題目上學生表現最差，平均正確率最低僅55.02%，比“面積和集合表征轉化——真分數”低了42個百分點．如圖2所示，涉及數軸表征的6道題目（即圖2中后6道題）正確率均低于其它題目．其中T4作為數軸表征與假分數表征結合的題目，正確率在所有題中最低，僅32%．此外，在“數軸表征轉化”相關問題上學生表現參差不齊，其平均正確率的標準差達0.31，接近“面積和集合表征轉化——真分數”的3倍．

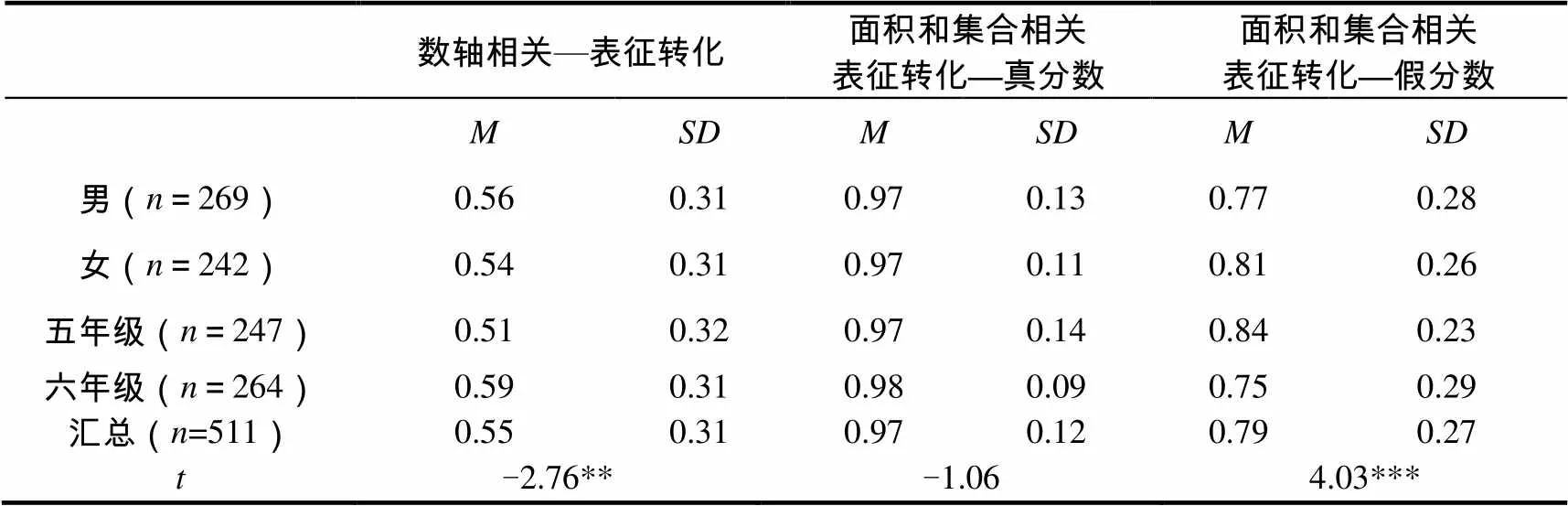
表4 學生在測試卷3個因子上的基本情況

注：**<0.01，***<0.001，檢驗是年級差異檢驗

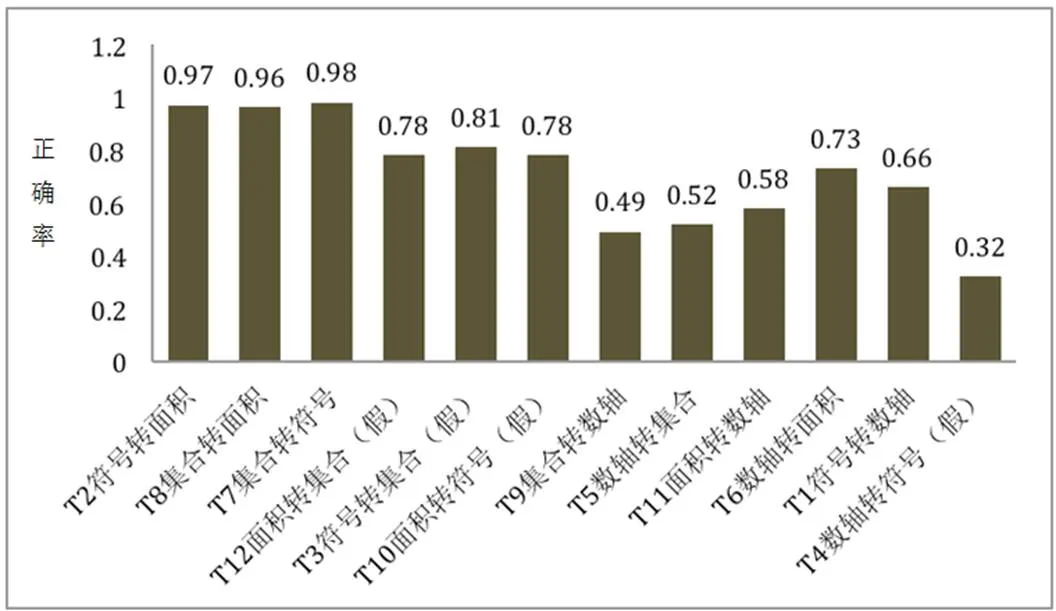
圖2 測試題目正確率條形圖

3.3 性別和年級差異

為檢驗學生在各個因素上的差異，進行了年級(2)×性別(2)的雙因子方差分析．結果顯示，不存在顯著的年級和性別間的交互效應（Wilks lambda=0.998，[3, 505]=0.31，=0.82）以及性別上的主效應（Wilks lambda=0.996，[3, 505]=0.65，=0.58）．不過存在年級上的主效應（Wilks lambda=0.945，[3, 505]=9.75，<0.001）．

為檢驗年級間的差異，進一步進行了檢驗（結果見表4）．在“面積和集合相關表征轉化——真分數”上不存在顯著的年級間差異（=0.29>0.05）．如圖3所示，六年級學生在該維度上的正確率略高于5年級學生．在“數軸相關表征轉化”維度上存在顯著的年級差異（=0.006<0.05）．如圖3所示，在該維度上六年級平均正確率（=58.71%）較五年級（=51.08%）有顯著的提高．在“面積和集合相關表征轉化—假分數”上亦存在顯著的年級差異（<0.001）．從圖3可看出，在“面積和集合相關表征轉化—假分數”相關問題上五年級平均正確率（=83.94%）反而優于六年級（=74.62%）．

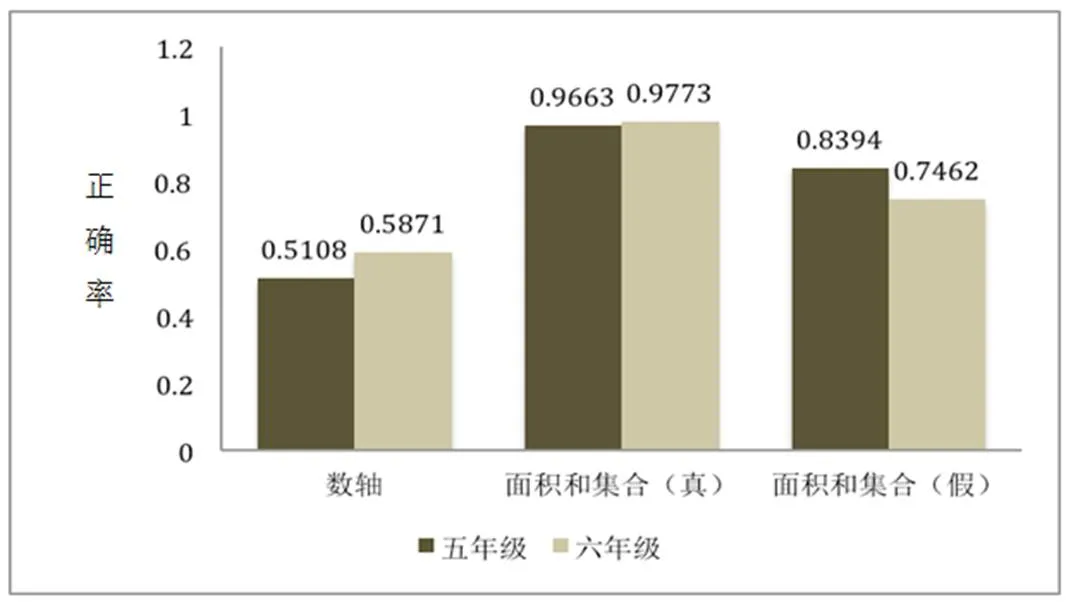
圖3 不同年級學生表征轉化任務表現條形圖

4 討 論

通過改編Kurt和Cakiroglu的分數表征轉化能力測試工具，研究調查了小學五、六年級學生的分數表征轉化能力．就具體調查內容而言，研究發現學生在面積表征轉化和集合表征轉化相關的問題上表現較好，但在數軸表征和假分數相關轉化問題上表現較差．

4.1 五六年級學生面積和集合相關表征轉化能力較強

如上所匯報，參與研究的小學生在面積和集合相關表征轉化問題上表現較好．其原因可能有如下3方面：第一，面積與集合所表示的“部分整體”概念對學生而言較易理解．多數學生在生活中已經接觸過如“平均分”、“幾分之幾”等與“部分整體”概念相關的知識和情景．此外，分數“部分整體”概念可以被學生原有認知中的整數概念所同化[11]．第二，“部分整體”概念是理解其它4個概念的基礎[8]，在分數概念教學中非常受到教師的重視，貫穿分數學習始終．第三，教科書編排與呈現方式的影響．通過對現行西南師范大學版小學數學教科書相關章節內容進行統計分析發現，面積與集合表征是最常用的圖形表征方式（約占圖形表征的92%，見表5）．這些都可能在很大程度上提升了學生面積和集合相關表征的轉化能力．

4.2 五六年級學生數軸相關表征轉化能力較差

如上所匯報，研究發現五六年級小學生在數軸相關表征轉化問題上表現最差，很多學生在相關轉化問題上出現較大困難．其可能原因主要涉及3方面：第一，數軸所表示的分數“測量”概念對學生而言較為抽象難懂．它要求學生理解分數是一個數，這與學生原有知識體系中的“整數”概念產生沖突，從而出現“整數偏向”的現象．此外，整數表示的是離散的數量，而分數表示的是無限可分的連續量[14]．這都造成了學生在分數“測量”概念和數軸表征上的困難．

第二，學生沒有理解面積（或集合）表征與數軸表征的本質區別．面積表示分數“部分整體”概念，數軸表示分數“測量”概念．對于分數（不為0），“部分整體”概念強調分數分子與分母的部分整體關系，而“測量”概念要求將看做一個整體，強調分數“數”的特征．學生將兩類分數表征混淆起來，誤認為數軸也表示分數的“部分整體”概念．此外，在訪談中還發現學生對單位“1”思想太過依賴，甚至出現“遇到分數問題，先找單位‘1’”的解題策略．這會使學生對分數概念的理解局限于“部分整體”，影響學生對分數多重概念和多元表征的掌握．

第三，教科書呈現與編排原因．通過對西南師范大學版小學數學教科書分數相關內容的分析比較，發現在分數表征的分布和呈現上存在3方面的問題．數量上，面積表征和集合表征占總表征數的92.08%，數軸表征出現頻次過少僅占7.92%（見表5）；分布上，面積表征幾乎貫穿所有分數相關章節，而數軸表征僅在五年級下冊分數的意義、分數大小比較、真分數和假分數、分數的基本性質以及分數小數中有所涉及，在五年級下冊分數加減法以及六年級的相關內容中沒有出現；知識呈現上，教材中對分數的界定是“把單位‘1’平均分成若干份，表示這樣的一份或幾份的數”，這有利于學生理解“部分整體”概念，但它沒有清楚界定分數“數”的特征，“表示一份或幾份”的數究竟是自然數還是分數[15]？含混的定義容易影響學生對分數“測量”概念的理解．

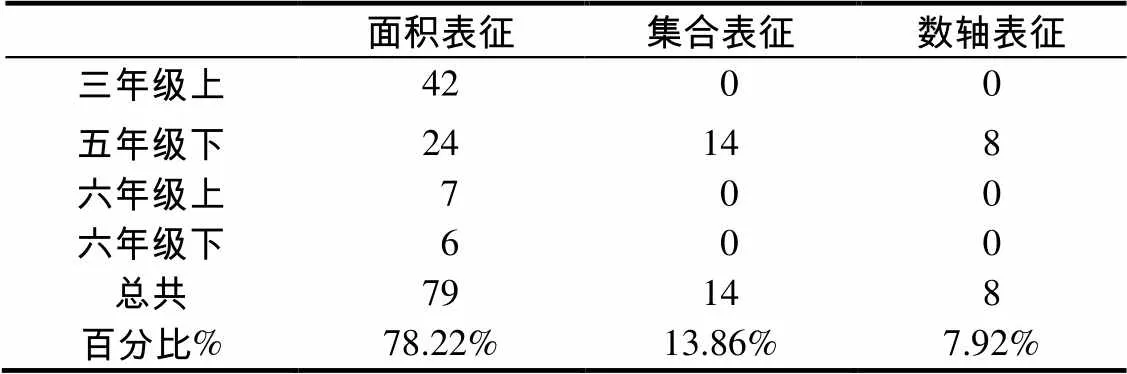
表5 西師版小學數學教材中3類分數圖形表征年級分布

4.3 五六年級小學生在假分數表征相關問題上存在困難

如上所述，通過調查發現五六年級小學生在假分數表征相關問題上也存在較大的困難．主要原因在于用集合表征假分數時，學生對單位“1”的選取．假分數的分子大于分母，此時的單位“1”不再是整個“圖形”．這與學生原有的分數認識產生沖突，學生較難理解單位“1”變成整個“圖形”的一部分．假分數表征要求學生更全面地理解分數“部分整體”概念．單位“1”是相對的，它的選擇需要根據實際情況進行重組和調整．

特別值得注意的是“面積和集合相關表征轉化—假分數”的正確率隨年級升高反而下降．這可能主要由于假分數相關內容僅在五年級下冊第一章第三節出現而六年級完全未涉及相關內容．隨年級升高，學生對真分數的理解不斷鞏固，而假分數及其表征逐漸被遺忘和混淆．

4.4 典型錯誤討論

學生在分數表征轉化的過程中遇到一些困難和障礙，問題集中于與數軸相關的表征轉化．根據測試卷結果分析，研究發現學生在分數表征轉化問題上的7種典型錯誤（見表6）．其中錯誤類型E1~E6具有共同的特征：學生在完成數軸相關表征轉化時，將數軸上標出的所有刻度看作整體，依據“部分整體”概念來尋找對應的點．以錯誤類型E1為例，題目要求學生將符號表征轉化為數軸表征，學生錯誤地將數軸所有呈現出來的所有刻度作為單位1（共14個刻度），取其中的8份（）．他們沒有意識到數軸上單位1是已確定的并且每個點代表確定的數值．這種錯誤出現的根本原因是學生沒有真正理解數軸表征所代表的“測量”概念，他們將“部分整體”概念與“測量”概念相混淆．錯誤類型E2中，題目要求學生將代表“部分整體”概念的集合表征轉為代表“測量”概念的數軸表征，概念的混淆導致錯誤率高達36.67%．

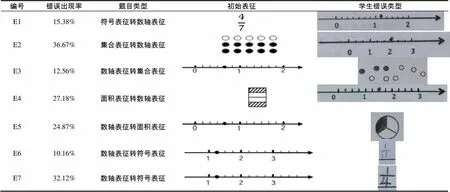
表6 分數表征轉化典型錯誤表

5 結論與建議

不同的數學表征給學生提供了不同解讀和思考問題的視角，所以提升學生數學素養的重要途徑之一在于培養學生對數學知識的多元表征能力以及在各種表征之間靈活轉化的能力．這不僅可以幫助學生理解不同表征與分數概念的關系，更可以促使其今后能靈活選擇合適的表征解決復雜分數問題．經調查，得出如下結論：五、六年級學生對分數概念的理解、假分數和分數數軸表征轉化任務上存在較大困難．這些研究結果可以對分數表征及分數表征轉化的教學提供些許建議．

5.1 課程內容和教學應注重多元表征

總的來說學生在分數表征轉化任務上存在不足，不能靈活地使用和轉化分數表征．比如在面積（或集合）表征與數軸表征轉化時，大量學生出現混淆，沒能理解這兩類表征的區別和聯系．而表征轉化能力是影響學生數學學習、問題解決及產生、有意義學習的重要因素[9]．基于此，課程標準和分數教學中都應注重多元表征以及表征轉化教學，幫助學生建立起全面的分數表征系統和知識結構．

首先，數學課程標準應該對分數“表征教學”以及“表征轉化”給予充分的重視，針對“表征”設立具體可操作的教學目標．課程標準是指導教材編寫和老師教學的重要依據，而《義務教育數學課程標準》[2]中未提到“多元表征”和“表征轉化”的相關內容．這自然會導致教師缺乏培養學生“多元表征能力”以及“表征轉化能力”的意識．

此外，在教學中教師需注重分數多元表征，讓學生在應用多元表征的過程中感受表征間的關系，從而建立更全面的分數表征系統．在不同表征間建立聯系的過程有利于加深學生的數學理解[16]．

5.2 教師和教材編寫者可在分數教學中更多使用數軸表征

學生在數軸相關轉化問題上存在較大困難，這主要由于數軸表征所對應的“測量”概念的抽象性，以及教材對數軸表征使用的欠缺．

基于此，在教學中教師首先要幫助學生理解“測量”概念．這需要學生經歷一個概念轉變的過程——即從離散性的整數系統轉變為連續性的有理數系統[17]．教師要讓學生感受整數擴充到有理數的過程，并利用數軸表征幫助學生理解分數與整數的關系，形成新的認知結構．

其次，在教材相關章節中可適當增加數軸表征的內容．特別是“分數加法”章節，數軸表征的使用可以使學生更容易理解和掌握分數加法的原理．這是由于數軸表征所表示的“測量”概念與分數加法運算聯系緊密，它是教授分數加法最適合的表征工具[18]．此外，對于教材中分數概念界定問題，張奠宙先生曾建議在定義中加上“大小”二字，既將“一個整體平均分成若干份，表示這樣的一份或幾份的大小的數，叫做分數”[15]．這樣的定義更強調分數“數”的特征，利于“測量”概念的理解．

5.3 假分數及假分數表征轉化應受到重視

假分數是分數的重要組成部分，調查結果顯示學生在假分數表征上存在較大困難，而這些困難一定程度上源于真分數表征及教材編寫的影響．基于此，教師需要幫助學生理解真分數表征與假分數表征在整體（單位“1”）選取上的區別，更全面理解“部分整體”概念．其次，教學中可用數軸來表征假分數，這樣一方面讓學生直觀地體會真分數小于1，而假分數等于1或大于1的特征；另一方面讓學生對真分數、假分數的意義有系統的認識，從而完善分數體系[19]．最后，教材編寫時也應充分考慮假分數知識的鞏固和螺旋上升，可在六年級分數章節中增加與假分數相關的知識和情景．

［參考文獻］

[1] National Council of Teachers of Mathematic.[M]. Reston, VA: NCTM, 2000.

[2] 中華人民共和國教育部．義務教育數學課程標準（2011年版）[M]．北京：北京師范大學出版社，2011．

[3] Goldin G A. Representation in School Mathematics: A Unifying Research Perspective [A]. In: Kilpatrick J, Martin W G, Schifter D.[C]. Reston, VA: NCTM, 2003: 275–285.

[4] 唐劍嵐．國外關于數學學習中多元外在表征的研究述評[J]．數學教育學報，2008，17（2）：30-34．

[5] Lesh R, Post T, Behr M. Representations and Translations among Representations in Mathematics Learning and Problem Solving [A]. In: Janvier.[C]. Hillsdale, NJ: Lawrence Erlbaum, 1987.

[6] 紀桂萍，焦書蘭，何海東．小學生數學問題解決與心理表征[J]．心理發展與教育，1996，（1）：29-32．

[7] Behr M J, Lesh R, Post T R, et al. Rational Number Concepts [A]. In: Richard A Lesh, ?Marsha Landau.[C]. New York: Academic Press, 1983.

[8] Behr M J, Harel G, Post T, et al. Rational Number, Ratio, and Proportion [A]. In: Grouws D A.[C]. New York: Macmillan, 1992.

[9] Behr M J, Wachsmuth I, Post T R, et al. Order and Equivalence of Rational Numbers: A Clinical Teaching Experiment [J]., 1984, (15): 323-341.

[10] ?Charalambous C Y, Pitta-Pantazi D. Drawing on a Theoretical Model to Study Students of Fractions [J]., 2007, 64(3): 293-316.

[11] 倪玉菁．五、六年級小學生對分數的意義和性質的理解[J]．心理發展與教育，1999，（4）：26-30．

[12] 張睆，辛自強．分數概念的個體建構——起點與機制及影響因素[J]．數學教育學報，2013，22（1）：27-32．

[13] ?Gonul Kurt, Erdinc Cakiroglu. Middle Grade Students’ Performances in Translating among Representations of Fractions: A Turkish Perspective [J]., 2009, (19): 404-410.

[14] ?Ni Y, Zhou Y D. Teaching and Learning Fraction and Rational Numbers: The Origins and Implications of Whole Number Bias [J]., 2005, 40(1): 27-52 .

[15] 張奠宙．“分數”教學中需要澄清的幾個數學問題[J]．小學教學（數學版），2010，（1）：4-6．

[16] 胡典順．美國學校數學教育中的“表征”及其啟示[J]．數學教育學報，2009，18（5）：72-74．

[17] 劉春暉，辛自強．五—八年級學生分數概念的發展[J]．數學教育學報，2010，19（5）：59-63．

[18] ?Keijzer R, Terwel J. Learning for Mathematical Insight: a Longitudinal Comparative Study on Modeling [J]., 2003, (13): 285-304.

[19] 朱新強．真分數和假分數——教學實錄與評析[J]．小學數學教育，2012，（Z2）：136-138．

[責任編校：周學智]

Investigation of Fifth and Sixth Students’ Abilities in Translating among Representations of Fractions

GUO Meng1, XIONG Yan-xi1, YANG Xin-rong1, CHEN Chao-dong2

(1. School of Mathematics and Statistics, Southwest University, Chongqing 400715, China;2. School of Mathematics, Sichuan University, Sichuan Chengdu 610000, China)

Representation of fraction is an important part of fraction, it also can help student understand the concept better. And the representations include region, discrete objects, number line, symbol and so on, which relate to the concepts of fraction. It’s significant for teachers to teach fraction. This paper modified the Translations among Representations of Fractions Test (Kurt & Cakiroglu) and used it to investigate 247 fifth and 264 sixth students, abilities in translating among representations of fractions. It finds that students have some difficulties in the transforming tasks that associated with number line and improper fraction. They cannot understand the difference between region (discrete objects) and number line. Besides, the sixth grade students perform better than fifth grade students in the tasks related to number line. Based on our finding, we suggest that math teachers should pay more attention to multiple representations of fraction, especially number line and representations of improper fraction. And translating among representation of fraction tasks can help students build a more comprehensive system of representations of fraction and improve students’ comprehensions of fraction concept.

representation of fraction; translating among representations of fraction; fraction concept; number line; elementary students

G420

A

1004–9894（2016）05–0049–06

2016–04–20

重慶市自然科學基金項目——小學生數學概念的發展過程：基于分數概念的研究（CSTC2011BB0010）

郭萌（1991—），女，四川樂山人，碩士研究生，主要從事數學教育研究．