初中數學課堂中教師對學生錯誤反饋的類型研究
——基于24節錄像課的分析

李 娜，莫雅慈，吳立寶

?

初中數學課堂中教師對學生錯誤反饋的類型研究
——基于24節錄像課的分析

李 娜1，莫雅慈1，吳立寶2

（1．香港大學教育學院，香港；2．天津師范大學教師教育學院，天津 300387）

數學課堂中，教師對學生錯誤的處理方式不同會引起不同的學習效果．若處理得當，學生的錯誤可以作為課堂討論的契機，促進教學；還能用來評價學生對數學的理解程度．通過4個不同城市24節初中數學錄像課，探究數學教師在處理學生錯誤時的行為，以期幫助教師更好地處理學生的錯誤．根據教師對學生錯誤反饋的性質，分為陳述型反饋和質疑型反饋．通過研究發現，教師更傾向于選擇用陳述型的語氣來處理學生的錯誤，同時有意識地提供機會讓學生自己糾正錯誤．教師應該為學生創造更多表達自己想法的機會，從學生表達中發現學生數學認知方面的問題，同時盡可能提供機會讓學生自己糾正錯誤，引起認知上的沖突，進而學生獲得更高層次的數學理解．

教師反饋；數學課堂交流；學生錯誤

1 研究背景

隨著課程改革的深入進行，作為教學中重要一環的教師提問，給予了相當程度的重視[1]，對課堂提問的研究較為普遍．最新的研究體現在課堂提問的有效性方面[2]，以及基于課堂錄像研究的課堂提問[3]．基于對數學課堂提問的錄像研究，Smith和Higgins認為關注點不應該只集中在教師的提問方面，還應該加強對教師反饋的研究，以創設更為開放自由的課堂交流環境，因為既不是問題本身也不是問題的類型限制了學生的反饋，而是教師對學生回答的反饋影響課堂互動的進行[4]．

提問之后，教師需要做出相應的反饋．教師在數學課堂上對學生的反饋是一種重要的教學行為，研究已經發現這一行為對學生的學習有重要影響[5]，尤其是當學生出現錯誤的時候．

課堂上對學生錯誤的討論或許能夠引導學生取得更大的進步[6]，Kazemi曾分析施行“高推動（high-press）”討論和“低推動（low-press）”討論的數學課堂，“高推動（high-press）”教師引導學生對錯誤的討論并創造一種讓學生感受到尊敬與安全的環境，更能引導學生取得成功．不但如此，數學教育研究者已經認識到學生的錯誤或是猜測能引起學生的討論，還能評價學生對數學的理解程度．

近幾年開始出現基于課堂錄像的有關教師對學生錯誤反饋的國際比較研究，Schleppenbach等人（2007）基于中美小學課堂的錄像研究發現[7]，無論中國還是美國的數學課堂，要想探究學生的錯誤，教師必須營造一個使學生不怕犯錯誤的課堂環境，并認為犯錯誤和討論錯誤很平常．其次教師不僅要推動學生去思考錯誤，而且通過提問學生解釋錯誤的方式來糾正錯誤．最終，希望教師和學生都不再害怕犯錯誤，并且能將錯誤看成是一個學習的機會．

想營造這種課堂環境，要注意以下4個方面[8]：（1）教師對錯誤的容忍程度與教師是否樂意了解并探討學生的錯誤有關；（2）對無關錯誤的評估，是指考慮學生的錯誤能作為學習的機會而不是作為考慮學生表現的負面指標；這種情況下，錯誤不能被懲罰，而是作為一個學習機會讓這個學生或是全班學生共同學習；（3）教師支持學生錯誤包括教師的耐心支持和支持學生自己修正錯誤；（4）若課堂上沒有教師的負面反饋，無論是口頭的還是非口頭的，這都暗示教師對學生錯誤既沒有不耐煩也沒有嘲笑．

2 研究設計

2.1 研究目的

基于以上得知，學生在課堂上所出現的錯誤不能被簡單粗暴地對待．教師若仔細考慮學生的錯誤，很多時候可以將學生的錯誤轉換為學習的契機，關鍵是教師如何處理學生的錯誤．因此，了解教師在課堂上對學生錯誤的處理方式尤為重要．Schleppenbach等人的研究針對小學數學課堂，為了更好地了解教師對學生錯誤的反饋，研究針對初中數學課堂：（1）開發一套可以用來分析教師處理學生錯誤的類型的編碼；（2）數學教師在課堂上處理學生錯誤的主要方式有哪些，這些方式各自出現的頻率；（3）不同授課類型與教師反饋種類的關系．希望通過這些研究結果來探討初中數學課堂的活躍氛圍與教師提問，學生回應和教師反饋的關系．

2.2 研究方法

2.2.1 樣本收集

基于所要研究的問題，對中國初中數學教師處理學生在課堂上所犯的錯誤有個初步的概觀．研究中所用的24節錄像課拍攝于4個經濟及教育較為發達的城市，分別來自東北地區，西南地區，北部地區和南部地區．為了便于表示的簡便，這4個城市分別命名為：NE、SW、NR和SU．每個城市有6節錄像課分別來自重點、普通及較差的學校，每一層級有兩節錄像課．因為研究中的所有錄像都來源于所參與的一個研究項目，項目中于2011年所收集的錄像約有120節，所以24節錄像課是有目的性選擇于這120節錄像課中．每個地區6節，每種類型的學校兩節，并且24節課中代數課有12節，幾何課12節．這種選擇方式考慮到地區差異，學校差異和內容差異對教師教學行為的影響，盡可能地保證教師對學生錯誤反饋的編碼的有效性．

2.2.2 錄像研究

若想要觀察課堂上實時發生的狀況，錄像研究有無可替代的優勢．具體體現在，錄像可以記錄動態的過程，可以回放進而觀察教師某些特定的教學行為等．曹一鳴在課堂錄像研究方面有比較多的成果[9~10]：“（1）首先確定觀察錄像所用的編碼；（2）借助某一軟件（如，Studiocode）在既定編碼的情況下進行錄像觀察，并統計相關數據；（3）結合統計數據與課堂錄像給出定量和定性的分析．”借助計算機軟件，可以更為精確地標記處某一編碼片段，統計出精確的

時間．

3 編碼及解釋

3.1 編碼選取及修訂

從國外研究文獻可以看出，學生的錯誤能用來探究學生學習方面的認知程度，而且近來有基于課堂錄像來研究教師對學生錯誤的反饋，所以這里重點研究初中數學課堂中教師對學生錯誤的處理方式．關于教師處理學生錯誤的編碼，基于Schleppenbach等人對中美課堂中小學教師對錯誤的反饋的研究，他們提出了一套適合中美小學數學課堂中教師處理學生錯誤的編碼（見表1）．這套編碼雖然是用于處理中美小學數學課堂中教師對學生的反饋，當經過多節課的預觀察之后，以及仔細觀察完24節課中的教師反饋類型之后，發現這套編碼仍然需要做些改動：首先，對學生錯誤回答的反饋類型的分類有些不妥，如“學生很快自動更正答案”應該不能稱之為“教師直接陳述型”，因為并不是教師在陳述，而是學生在陳述，但是教師是認可的．其次，有些反饋類型在初中課堂上幾乎不會出現，例如，初中的學生很少會出現讀不懂題目的情況，而對于小學生來說，尤其是低年級的小學生，因為認識的漢字有限，有些時候需要教師對問題進行進一步的解釋或闡述．

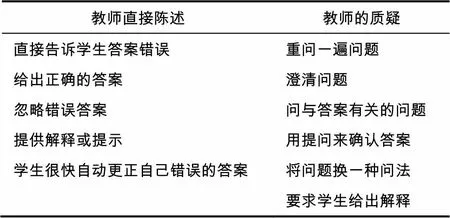
表1 對學生錯誤的反饋方式

基于此，對此編碼所做的改動主要體現在以下幾個方面：在第一種反饋類型之下，多數情況之下，當聽到學生的答案錯誤之后，教師忽略錯誤答案的同時會選擇讓其他同學或是自己給出正確的答案；在第二種類型的反饋之下，教師將問題換一種問法，其實是教師進一步澄清問題的一種方式．再結合其他因素的考慮，如反饋類型的區分程度以及可操作性等，故將編碼修正（見表2）．

表2 編碼修正

為保證編碼的有效性，在對此次錄像進行編碼之前，第一位作者曾作為某一項目的參與人員接受過編碼以及軟件使用的培訓．此次利用NVivo 8.0，首先標記出各個預備編碼的片段，再次進行查看和校驗的時候，可以直接查看這些片段即可．同時，其他人還可以進行編碼，然后比對，進而商討編碼的有效性．

3.2 編碼解釋示例

編碼總數有9個，選取其中4個提供示例來解釋編碼，其中括號中的文字用來解釋教師或學生的非語言行為；括號中的斜體字是說明教師和學生的行為以及對教師反饋行為的分析．

3.2.1 問與答案有關的問題

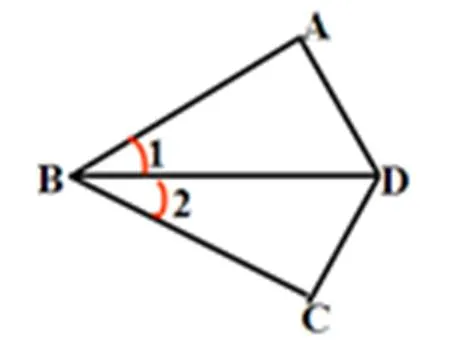
圖1 例題

解釋：當同學們回答不出來或是回答不正確的時候，教師或許會問與答案有關的問題來幫助學生找到解決問題的思路．

重慶教師4課堂上的一個教學

片斷：

例1 已知：如圖1，=，∠1=∠2，△和△全等嗎？

變式1：現在例1的已知條件不改變，而問題改變成：問=，平分∠嗎？

問題背景：教師先讓一個同學到黑板上做例1，該同學做得非常好，教師就以這位同學的解法來向全班同學講解，然后變式1的問題才顯示在PPT上．

課堂實錄

師：現在看變式1，例1中的條件不變，將問題改為=，平分∠嗎？你能證明嗎？

很多同學：能．

師（）：你能證明嗎？思考一下．

生1：呃，……

師（）：能證明嗎？

很多同學：能．

師：好，能證明的同學站起來說一下怎么證．（）

師（繼續問）：其他同學呢？積極點啊！（）

生2：已知條件告訴我們，在△中，=，∠1=∠2，然后=，又等于……

下面同學（）：重了．

師：那你說說大致需要做多少，不需要說這么具體，那你覺得我們要證明=，是∠的平分線的話，需不需要證明全等？（）

小部分同學：需要．

師（）：需不需要？

大部分同學（）：需要．

師：需要，對不對，那想想怎么修改一下，補充一下，你（）上黑板試著寫一下，通過證明全等，來解決我們的問題．

（）

3.2.2 通過提問來確認答案

解釋：教師有時候明明知道學生的答案錯誤或是不正確，但是教師一般不采取直接告訴學生答案的方式，而是通過再問一次“是這樣嗎？”，“其他同學的答案也是這樣嗎？”等疑問，來確認答案．

北京教師5課堂上的一個教學片斷：

問題背景：教師在講解完同底數冪的除法運算法則之后，先練習了兩個較為簡答的例題，又給出了一個稍顯復雜的例題．

課堂實錄

師（）：這是不是咱們要研究的同底數冪的除法？

生（）：是．

師：符合這個（）嗎？

生（）：符合．

師：既然符合，那么同底數的底是什么啊？

生（）：括號．

）

師：都是這么做的嗎？（）

生（）：是．

生（）：還能再化簡．

接下來是去括號的過程．

3.2.3 要求其他學生給出解釋或補充

解釋：教師若覺得學生的答案不滿意，或許會選擇讓其他同學來解釋或補充．

沈陽教師2的課堂上的一個教學片斷：

背景：教師讓學生做書上的一道關于用直角三角形全等的題目，因為教師沒有PPT，也沒有在黑板上書寫這道題，所以具體的題目內容不得而知．教師指定一位女同學到黑板上去做這道題．

（）

課堂實錄

師：對這個同學的做法，誰還有什么不同意見？

（）

師：有誰還發現這道題有什么不恰當的地方了嗎？

（）

生：這道題用到直角三角形全等條件時都沒在后面寫上HL．

（這是第二位同學的補充）

師：對，說得很好，這個同學太過分了（），剛開始學，就不寫根據．

3.2.4 忽略或者分析錯誤答案同時提供正確解釋

解釋：教師直接忽略錯誤答案，給出自己認為完美的答案．

沈陽教師2的課堂上的一個教學片斷：

背景：教師布置了一道題，讓同學們分組討論，幾分鐘過后，教師讓其中的一個小組指派一名代表，站起來說說證明過程．

生：（）

師（）：坐下．這道題應該怎么樣來處理呢？（）

以上是對編碼的課堂實錄的解釋，希望能通過這些解釋來更好地說明編碼的合理性，同時也說明這套編碼可以用于分析對初中數學課堂中教師對學生錯誤的處理方式．

4 教師對學生錯誤的處理方式的統計結果

編碼結束之后，選擇對教師的反饋次數進行統計．因為在進行編碼處理的時候，已經發現教師在處理初中學生的回答錯誤或是不完全正確的答案時采取的策略有傾向性，所以希望通過次數的統計發現教師傾向于選擇何種策略來處理學生的錯誤或是不完善的答案．

4.1 對學生錯誤反饋的種類

先看第一類：陳述型的錯誤反饋類型的數據統計結果（見表3）．從下面的統計中得知，24位教師的反饋錯誤總次數為92次，而在這個表中看出：（1）陳述型的反饋錯誤總數為52次，約占57.6%；（2）直接告訴學生答案錯誤或是忽視錯誤答案的情況依然存在，將近10%；（3）教師提供解釋或提示與學生很快自動更正錯誤的百分比接近．

從表4中看出：（1）質疑型的反饋次數為39次，約占42.4%，相比陳述型的反饋錯誤類型，少了15.2%；（2）通過提問來確認答案的次數最多，其次是要求其他學生對此錯誤或是不正確的答案給予解釋；（3）僅僅有一次是教師對問題進行進一步的澄清．

表3 陳述型反饋（次數）

表4 質疑型反饋（次數）

4.2 反饋次數與教師數量

為了較為方便地觀察教師的反饋頻數，對教師的反饋次數的數據進行了整理（如圖2）．從圖中可以看出，反饋次數從1次到7次，多數集中在3，4，5次，更為具精確一些來講，教師的平均反饋錯誤次數約3.9次．

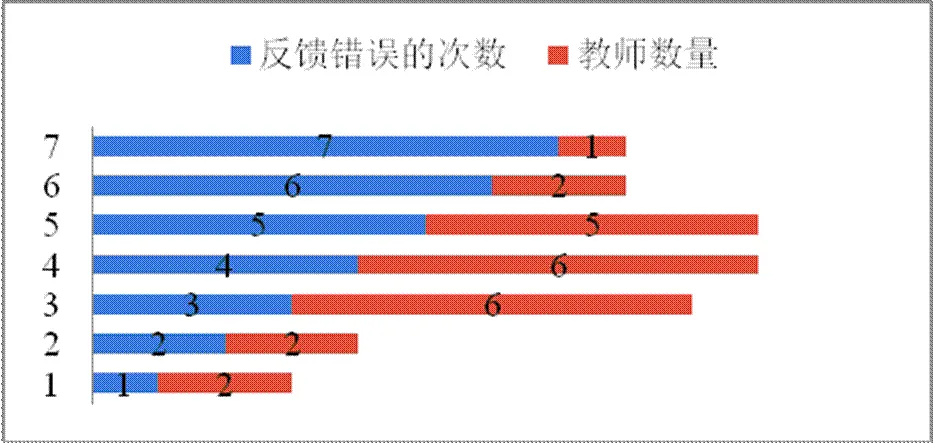
圖2 反饋次數與教師數量

4.3 反饋種類與課程類型

研究者[8]數學課的類型，尤其是幾何和代數課是否會影響到教師對課堂錯誤的管理和教師的回應類型存在爭議．總體來看，代數課堂中出現的錯誤數45次，幾何課堂出現的錯誤數47次．從總次數來看，差異不大．但是在具體到教師的反饋類型時，有些差異還是較大．代數課中教師傾向于用陳述型的反饋，尤其是第二種陳述型的反饋（見表5）．幾何課中，教師更傾向于用質疑性的反饋，尤其是通過提問來確認答案，代數課中僅僅出現3次，幾何課中卻有13次（見表6）．

表5 陳述型反饋（幾何與代數）

表6 質疑型反饋（幾何與代數）

5 結論與啟示

學生在課堂上出現的錯誤，可以用來評價學生的學習成果，也可以用來診斷學生的學習情況，目的的不同主要是由教師的反饋來決定．教師不同種類的反饋會給學生的學習帶來不同的影響．基于24節錄像課分析，分析教師反饋方式的框架首先完成，為后續研究者提供可供借鑒的分析工具；依據此框架，不同方式的頻率可以被統計，由此可以為教師的反饋方式提出相應的建議；考慮到幾何與代數的教學差異，教師的反饋方式也出現差異，藉此提醒教師在講授不同內容時要注意．

5.1 反饋類型有差異

總體來講，陳述型反饋多于質疑型反饋，且教師傾向自己提供正確的解釋．24位教師的反饋錯誤總次數為92次，其中陳述型的反饋錯誤總數為52次，約占57.6%．教師在處理學生所犯的錯誤時，教師更傾向于選擇用陳述型的語氣來處理學生的錯誤．選擇這樣的語氣，更容易讓學生接受和理解，便于師生之間的對話有效進行．在這種情形下，教師又往往很少會忽視不理或是任意打斷學生的錯誤，更多地傾向于對學生的錯誤進行校正，幫助學生自己認識到錯誤，幫助學生克服認知上的矛盾，從而習得新知識．但是教師在其中扮演的主導者的角色還是特別明顯，雖然教師不太會直接忽略錯誤答案，但是大部分是教師解釋錯誤答案并同時提供正確的解釋．課堂的權威性還是在教師．當教師選擇用質疑型的語氣時，傾向于通過提問來確認答案的正確性，或是讓其他同學來解釋為什么錯了．這樣做有利于培養學生分析問題，判斷問題的能力，從而善于成為學習的主人，而不是被動地接受教師的傳授．這同時也給予了其他同學參與課堂交流的機會，對于同伴的想法，學生可能會敢于表達自己的想法，提出質疑或給出論證．

這樣的氛圍下，學生恐怕還是傾向于選擇服從教師的話語，而不是充分地表達自己的想法．教師在教學中要更以平和親切的態度去對待學生的錯誤，讓學生不但不害怕犯錯還要學會正視自己的錯誤．后續研究中，可以嘗試比較這兩種類型所帶給學生的學習影響．

5.2 反饋次數的比較

教師對學生錯誤的反饋次數集中在3~5次之間，17位教師的反饋頻數集中在此區間．更為具體一點來說，教師的平均反饋錯誤次數約3.9次．這也間接說明課堂上學生出現的錯誤數也基本維持在3~5次之間．這一點與已有研究的結果相符，研究發現，中國的數學課堂提供一個允許學生犯錯誤的環境，在分析視頻的過程中，確實能聽到教師為了鼓勵學生回答問題，不停地說“不要害怕”，“大膽地說”，“說錯了也不要緊”，即使這樣，絕大多數初中的學生在沒有十足把握的情況下還是不會選擇站起來回答問題，除非被教師點名，這時候才帶著些許的不自信來回答問題．雖然課堂中教師有意識創造一種允許學生犯錯誤的氛圍，但是學生還是擔心犯錯誤在老師以及同學面前出丑．

5.3 反饋因內容有差異

代數課中陳述型反饋多于質疑型反饋；幾何課中質疑型反饋多于陳述型反饋．代數課堂中，陳述型的反饋出現的頻率較高．這應該是與代數的學習有關，很多時候，代數問題可能是簡單的一問一答，或是要求學生嚴格按照代數公式來計算，這樣的課堂氛圍看著很活躍，教師一個問題接一個問題，出現錯誤答案，教師直接說不對或是另外找同學回答或是教師自己解釋，但是學生在這種師生交流中是否真正實現了思維的碰撞還是最終回到了記公式的套路上．幾何課堂中，教師傾向于用質疑性的反饋，出現的頻率是代數課的兩倍．這應該與幾何課中有很多證明性的學習有關．教師傾向于通過提問來確認答案，或是要求學生給出解釋，在教師提問確認或是學生解釋的過程中，教師在檢查學生的證明思維是否清晰，學生在表述的過程中可以進一步梳理自己的證明思路．在這樣的問（師）—答（生）—反饋（師）—學回應（生）的過程中，其實是一種思維的交流過程．課堂氛圍可能看起來似乎不是那么活躍，但確實能幫助學生在證明、推理方面進行訓練．

授課內容的不同也會造成教師反饋方式出現頻率的不同，若針對不同的教學內容，教師應要考慮反饋方式的差異．

6 討論及不足

首先，此編碼框架雖然不能涵蓋全部的教師對課堂中學生錯誤的處理種類，但是可以提供一個很清晰的輪廓關于教師對學生在課堂上錯誤行為的管理．后續研究者可以用次框架放在不同背景中進行驗證并改進，比如高中數學課堂；還可以用來比較新手教師與專家型教師的不同．

其次，教師通過提問讓學生主動參與到課堂教學中來，但是學生的回答肯定不可能那么完善，即使學生的想法不完善或是錯誤，也要嘗試給出提示以引導學生自己發現知識．教師通過問題幫助學生學習，這也符合新課程政策的影響，教師有意識地鼓勵更多的學生參與到課堂對話中[11]，讓學生在課堂中能勇敢地進行數學交流．因此，教師要提高問題的質量，減少短平快問題的數目，盡量準備能引起學生思考的問題，尤其是在代數課堂中，不要只準備口頭回答，口頭演算的問題．

除此之外，學生的錯誤還可以作為診斷學生學習情況的一個媒介，為教師的教學改善提供幫助．教師可以通過學生的錯誤來反思自己教學中對于學生的認知是否存在不足，反思怎樣才能更好地將知識與學生的認知有效結合起來．實際中，研究發現[10]，其實中國的課堂是一個允許學生犯錯誤的環境，在分析視頻的過程中，確實能聽到教師為了鼓勵學生回答問題，不停地說“不要害怕”“大膽地說”“說錯了也不要緊”．學生只有不怕犯錯誤，才能更積極地去思考并回答教師的問題，進而教師再依據學生答案提供合適的幫助．

還有就是教師對學生回答問題的即時反饋也是一種對學生即時的評價，所以這種評價不能只限于答案的對錯上，而是著重學生對知識的理解程度．教師應盡可能判斷學生的認知程度，根據其認知程度，幫助學生學習．這就要求教師都需要精心組織材料，引導學生觀察和思考，對學生提出一定的目標，并對學生的知識掌握情況進行評價[12]．

［參考文獻］

[1] 李鵬，傅贏芳．論數學課堂提問的誤區與對策[J]．數學教育學報，2013，22（4）：97-100．

[2] 溫建紅．數學課堂有效提問的內涵及特征[J]．數學教育學報，2011，20（6）：11-14．

[3] 葉立軍，胡琴竹，斯海霞．錄像分析背景下的代數課堂教學提問研究[J]．數學教育學報，2010，19（3）：32-34．

[4] Smith H, Higgins S. Opening Classroom Interaction: The Importance of Feedback [J]., 2006, 36(4): 485-502.

[5] Zahorik J A. Classroom Feedback Behavior of Teachers [J]., 1968, 62(4): 147-150.

[6] Kazemi E. Discourse That Promotes Conceptual Understanding [J]., 1998, 4(7): 410-414.

[7] Schleppenbach M, Flevares L M, Sims M L M, et al. Teachers’ Responses to Students’ Mistakes in Chinese and U.S. Mathematics Classrooms [J]., 2007, 108(2): 131-147.

[8] Tulis M. Error Management Behavior in Classrooms: Teachers’ Responses to Student Mistakes [J]., 2013, (33): 56-68.

[9] 曹一鳴，李俊揚，大衛·克拉克．數學課堂中啟發式教學行為分析——基于兩位數學教師的課堂教學錄像研究[J]．中國電化教育，2010，（10）：100-102．

[10] 曹一鳴，賀晨．初中數學課堂師生互動行為主體類型研究[J]．數學教育學報，2009，18（5）：38-41．

[11] 李小青，倪玉菁．小學數學課堂的教師教學質量研究[J]．數學教育學報，2013，22（4）：54-57．

[12] 曹一鳴．數學教學中需正確處理的幾個關系[J]．中學數學教學參考，2003，（8）：1-3．

[責任編校：周學智]

Types of Mathematics Teaches’ Feedback to Students’ Mistakes in Secondary School

LI Na1, Ida Ah Chee MOK1, WU Li-bao2

(1. Faculty of Education, The University of Hong Kong, Hong Kong, China; 2. Teacher Education College, Tianjin Normal University, Tianjin 300387, China)

This study investigated mathematics teachers’ feedback to students’ mistakes based on analyzing 24 videotaped lessons. Two categories of teacher response are provided and used to analyze teacher’s behavior in dealing with student’s mistakes. One is declarative response which include telling the student the answer directly; ignoring the wrong answer and then giving the correct answer; providing explanation or indication; and students spontaneously correcting themselves. The other is challenge response which includes clarifying the question; asking a question related to the answer; asking certainty or agreement; asking the student provide explanation; and asking other students provide explanation. The result indicated that the teachers intended to adopt declarative feedback to students’ mistakes and provide chance for students to refine their answers.

teacher response; student mistake; mathematics classroom communication

G632.0

A

1004–9894（2016）05–0055–06

2016–04–05

美國National Science Foundation支持的國際比較項目——Cross-National Comparison of School and District Supports for High-Quality Mathematics Instruction in the U.S. and China（DRL-1321828）

李娜（1986—），女，山東日照人，博士生，主要從事數學教育研究．