類題同法 減負增效

陳彬彬

（南安市侖蒼中學，福建南安362300）

類題同法 減負增效

陳彬彬

（南安市侖蒼中學，福建南安362300）

類題同法是在扎實做好一道題的基礎上，通過“變式練習”“多題一解”“拓展應用”等策略，讓學生在自主建構過程中融會貫通，擺脫“題海戰術”，減輕課業負擔，實現做一題，會一類，通一片的目的。

類題同法；減負增效

對數學教材中的例題、習題、復習題進行教學時，教師不能就題做題，要引導學生以題論法、以點帶面，對同一類數學問題應前后對比，找出它們的區別和聯系，感悟其中蘊含的數學思想，做到舉一反三。現以華東師范大學出版的八年級上冊第14章《勾股定理》總復習題中某道應用題為例，談談筆者的想法和一些做法。

一、自主建構夯實數學基礎

學生審題能力、畫圖基本功、數學語言表達的規范性，需要老師不斷指導，讓學生讀懂題意，進而能進入問題情境在初步探究中自主建構。

圖1

例如，筆者請學生解答華東師范大學出版的八年級上冊第128頁第12題（如圖1）：一根竹子，原高一丈，蟲傷有病，一陣風將竹子折斷，其竹梢恰好抵地，抵地處離原長竹子處3尺遠，問原處還有多高的竹子？

這是一道實際應用題。解答時需要逐句逐字分析，已知條件有“竹子原高一丈，抵地處離原長竹子處3尺遠。”，未知條件是“原處還有多高的竹子。”課堂中老師不能急于求成，應盡量少講，甚至不講，只在學生審題有困難時才給以幫助。比如關鍵詞“原高一丈”是什么含義，隱含條件是什么（“竹子與地面垂直。”）特別提醒學生要自己畫圖，把實際問題抽象為“如圖2，在R t ΔABC中，∠C=90°，AC=3，BC+AB=10.”的數學問題。雖然耗時長一點，但學生經過親歷解決問題的全過程，中途出現錯誤和偏差及糾正，學生印象會更深刻，理解更透徹，基礎更扎實。

問題解法如下：設BC=x尺；則AB=（10-x）尺，

∵∠C=90°，

∴AC2+BC2=AB2，

即32+x2=（10-x）2，

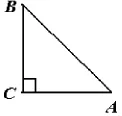
圖2

二、課堂“說題”理順兩種關系

在數學課堂上，就某個知識的重點或難點設計一道相關的數學問題，請學生進行現場“說題”，分析并說明解題思路，可以理順“教與學”“師與生”關系，從“先教后學”變成“先學后教”，從“教師主宰”變成“學生主體”。

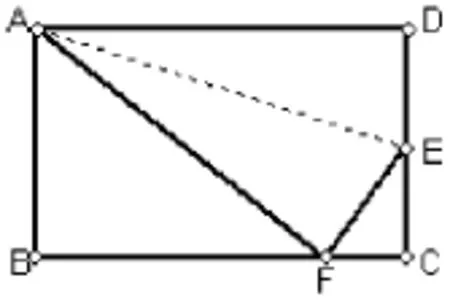
圖3

例如，筆者在完成教材總復習題后，又改編原華東師范大學出版的八年級上冊第63頁第11題（2006年版），如圖3：“在矩形ABCD中，AB=5 cm，在邊CD上適當選定一點E，沿直線AE把△ADE折疊，使點D恰好落在邊BC上一點F處，且ΔABF的面積是30 cm2.求此時AD的長.”

增設第2問：DE的長為多少時才能滿足條件？

傳統講授方法是教師分析題意，設計問題串提問學生，書寫解答過程，省時省力，節奏流暢。整個過程教師主導講課，學生被動聽講，教師辛苦，學生痛苦，教學效果可想而知。

筆者在課堂上則是讓學生到講臺現場“說題”，學生不僅僅停留在“我要怎樣解題”上，更重要是闡述“為什么這樣解題”，學生說題流程如下：一是說明題目來自哪里，與原例題對比，有何聯系和區別；二是說明題目考查的是矩形性質、三角形面積公式、勾股定理和圖形折疊的性質，考查方程思想和模型思想；三是說明題目已知條件是在R t△ECF中，CF=1 cm，EF+EC=5 cm，四是說明解題思路及所采用的方法，不妨設DE=xcm，則EF=DE=xcm，EC=（5-x）cm，用方程思想來解決問題；五是說明做好這道題后，今后碰到類似題目時，要如何實現類題同法，減負增效。

在課堂上，學生熱情參與，成為學習的主人，教師成為數學學習的共同體。長期下來，學生將逐步養成“想題、做題、說題”的習慣。

三、多題一解發展學生思維

要加深學生對某一數學思想的深刻理解，需要在不同的題目背景下完成。教師可以適當改編原題的條件，進行變式練習；教師也可以精心組合同一類習題，讓學生通過小組合作，共同分析、比較、歸納這類習題有什么聯系和不同點，整合它們的解題策略，領會同一數學思想。

例如，筆者設計如下4道習題，請學生歸納它們的共同特征：

習題1：如圖4，將邊長為8㎝的正方形ABCD折疊，使點D落在BC邊的中點E處，點A落在F處，折痕為MN，求線段CN的長.

習題2：如圖5，矩形紙片ABCD中，AB=4，AD =3，折疊紙片使AD邊與對角線BD重合，折痕為DG，求AG的長.

習題3：如圖6，矩形紙片ABCD中，AB=3，AD =9，沿對角線BD折疊，使C落在處，交AD于E，求AE的長.

習題4：如圖7，矩形紙片ABCD中，AD=4 cm，AB=10 cm，按如圖方式折疊，使點B與點D重合，求折痕為EF的長.

通過對題目進行初步分析，學生將會有如下發現：

習題1的R t△CEN中CE=4，EN+CN=8；

習題2的R t△A′BG中A′B=2，A′G+BG=4；

習題3的R t△ABE中AB=3，AE+BE=9；

習題4的R t△ADE中AD=4，AE+DE=10.

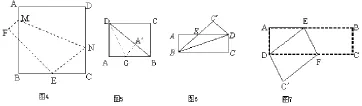
通過歸納，學生得出如下結論：“四道題雖然題目背景不一樣，但都有一個共同特征：在一個直角三角形中，如果有一條邊長已知，另二條邊長的和也已知，我們可以根據勾股定理，構造一個方程，從而求出另二條邊長”，因此可多題一解。

學生由于知識儲備和經驗水平有限，剛開始要完成“多題一解”有困難，需要教師課前認真學習《課程標準》，研讀教材，分析學情，精心備課，把同一類題目整合起來.經過一段時間訓練，學生做完許多數學題后，就會逐步養成題后反思的習慣，時常歸類整理數學題，領會通用的數學思想。

四、拓展應用提升綜合能力

在具體情境中，幫助學生獲得基本的數學思想，提高動手操作和數學思考能力，增強發現和提出問題的能力、分析和解決問題的能力是數學課程重要目標。

例如：如圖8，矩形紙片ABCD中，AB=8，點G在BC上，將紙片沿著GF折疊.折痕的另一端F在AD邊上，B點的對應點E在長方形內部，E到AD的距離為2 cm，BE=10時，求AF的長.

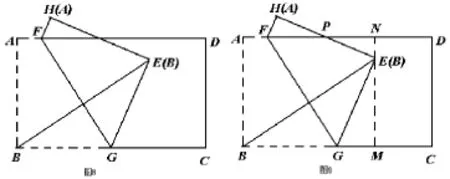
這是一道折疊操作題，屬于綜合性問題，主要考查折疊性質、圖形的性質、思維能力。解決此類問題時，要求學生先動手折疊一下，熟練掌握圖形（三角形或矩形）的性質和判定、折疊的性質，解題的思路要把求AF的長轉化為利用△FPH∽△EGM求出HF的長。解題的關鍵是應用“R t△GME中，一條邊長EM已知，另二條邊長GE、GM的和也已知”模型，設GE=BG=x，根據勾股定理，用方程方法求解。

在完成這道綜合題活動中，學生掌握獲取信息的能力，鞏固了數學基本知識，提高了動手操作能力，學會了“數學方式的理性思維”，體驗了建立模型、解決問題的過程，綜合能力得到較好提升。

總之，數學學習方式是多樣化的，不同學習內容，不同課型應采用不同方法，以獲取最佳學習效果。類題同法是減輕學生課業負擔的一種重要方式，它可以真正提高教學效益，讓學生享受學習樂趣。

［1］教育部.義務教育數學課程標準（2011年版）［S］.北京師范大學出版社，2012.

［2］潘振南.淺談中學數學“說題”教研活動［J］.學苑教育，2014（7）.

［3］朱海東.例談數學解題教學“三步曲”［J］.中學數學，2014（23）.

（責任編輯：王欽敏）