利用離散Hopfield網絡分析高等數學教學模式

苗鵬，范留軍

?

利用離散Hopfield網絡分析高等數學教學模式

苗鵬1，范留軍2

（鄭州科技學院 1. 基礎部，2. 土木建筑與工程學院，河南 鄭州 450064）

借助離散Hopfield神經網絡對現有高等數學教學模式進行分析討論，以尋求更加合理的教學模式，從而達到更好的教學目的．將抽象的教學模式轉化為計算機語言，進而建立離散Hopfield神經網絡，然后對現有幾種高等數學教學模式進行分析．運用所建立的離散Hopfield神經網絡對給出的實例進行仿真，并做出總結，為今后高等數學教學提供參考．

離散Hopfield神經網絡；高等數學；教學模式；實例仿真

神經網絡自上世紀中期首次被提出以來，已經被廣泛應用到工程與科學領域，如預測地下水位，預測股市的開盤價，進行模式識別[1]、混沌控制[2]、求解優化問題[3-4]、解時變Sylvester方程[5]以及診斷柴油機故障[6]等方面．與傳統的方法相比，神經網絡具有其獨特的特點：神經網絡由特定的動態方程所確定，并且可以借助計算機運用傳統的ODE方法求解．這就決定了神經網絡具有廣泛的使用價值．雖然關于高等數學教學模式已有一些研究[7]，但是基于神經網絡的教學模式分析并應用到教學中的研究還鮮有學者涉足．在關于神經網絡研究的基礎上[8-11]，以及考慮到各種教學模式對高等數學教學的重要性[12-13]，本文將離散Hopfield神經網絡運用到分析高等數學教學模式的效果，從而對教學工作起到一定的指導借鑒作用，具有重要意義.

1　高等數學教學模式分析

高等數學是工科、經管等有關專業必開的一門公共基礎課．其授課內容、解題方法和數學思想具有高度的抽象性和概括性，一直以來是大學基礎課中學生感覺比較難學的一門課程．

1.1注重培養學生的創新思維和應用能力

1.1.1把數學建模思想滲透到教學中教師適當地將數學建模的思想融入到教學過程中，不僅加深了學生對概念的理解，而且提高了學生應用數學的能力和學習數學的興趣．

1.1.2增加數學實驗將數學實驗這一實踐性教學內容嵌入教學中，通過解決豐富多彩的實例，能夠讓學生充分體會到數學的魅力和數學應用的重要性，以及提高學生借助計算機親自動手處理實際問題的能力．

1.1.3加強與專業知識的有機融合此種教學是一種開放式、互動式的現代教學方法，不僅能啟發學生關注實際問題，而且有利于學生智力的開發及創新能力的培養．

1.2靈活運用形式活潑的教學手段與方法

1.2.1問題驅動法在數學實驗和應用案例的教學過程中，采用研究式的教學方法．

1.2.2多媒體課件與板書相結合板書教學具備教學結構完整和教學思維縝密等諸多優點，但也存在教學信息量少和不利于培養學生想象力、創造力的弊端．多媒體教學具有其獨特的優勢，可以利用它的圖畫特性將抽象的、理論的東西形象化，將空間的、難以想象的內容具體化．把抽象思維和形象思維緊密地聯系起來，把分析與幾何有機地融合起來，有利于培養學生的形象思維能力和空間想象能力．

1.2.3網絡課程輔助教學一個好的高等數學網絡教學系統可以激發學生學習的興趣，培養自學能力，以及整理和加工數學信息的能力．

1.3考核方式

從多方面對學生的能力進行考核，主要包括：考試成績，解決問題的能力，邏輯思考能力以及專業知識結合能力等方面．

2　離散Hopfield神經網絡的建立

由于教學模式是比較抽象的各種形態，直接作為網絡的輸入是計算機無法識別的，因此建立神經網絡之前要將抽象的教學形態轉化為計算機可以識別的機器語言．

首先，將各種教學形態用不同的字母符號表示．做出如下假設，A1為數學建模思想滲透到高等數學教學；A2為增加數學實驗；A3為加強與專業知識的有機融合；A4為傳統教學；B1為問題驅動法逐步展開新的教學內容；B2為多媒體課件與板書相結合的教學方式；B3為采用網絡課程進行輔助教學；B4為按照課本板書式教學；C1為考試成績；C2為解決問題能力；C3為邏輯思考的能力；C4為專業知識結合能力．

其次，將這些形態作為神經網絡的輸入：=[A1，A2，A3，A4，B1，B2，B3，B4，C1，C2，C3，C4]，其中：向量的取值代表教學過程中采用的教學模式，如B1=1，代表在教學中運用了問題驅動法逐步展開新的教學內容，反之B1=0表示沒有采用．

最后，運用MATLAB中的newhop函數創建離散型Hopfield神經網絡．

3　實例討論

為了形成鮮明的對比，選取區分度較大的4個班級作為考察對象，Class1~4采用的教學模式、手段方法、考核方式和期末綜合成績過關率（大于等于60的比例）見表1．其中A1~A4的數值代表時間且和為100，B1~B4，C1~C4的值為１表示采用了這種方法，為0表示沒有采用，的數值80表示過關率為80%及以下，85表示過關率為80%~85%，90表示過關率為85%~90%，95表示過關率為95%及以上．從而可以將這4個班級分為4類（見表2）．

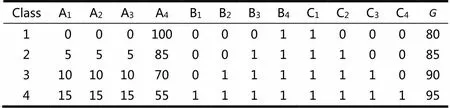
表1　4個班級原始數據

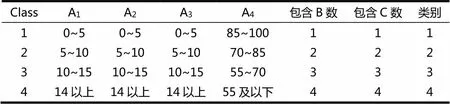
表2　將4個班級分為4大類

用這4個班級數據進行學習訓練，然后預測4個班級所屬的類別，見表3.

仿真結果見圖1．由圖1可見，所設計的離散型Hopfield神經網絡能夠很好地預測出班級一，二，三，四所屬分類分別為1，2，3，4．從而在教學過程中要針對某一種教學模式或者評價標準適當改進，更有利于提高班級綜合過關率．

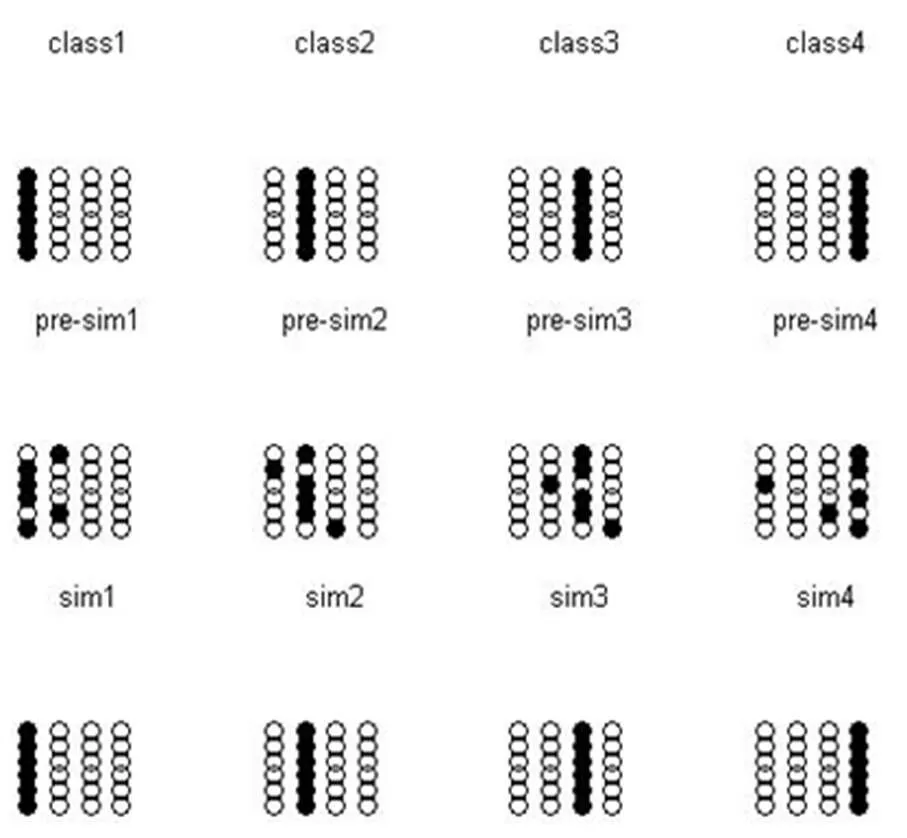
圖1　仿真結果

4　結語

本文借助于離散Hopfield神經網絡，通過理論分析與具體的案例仿真展現了現有的高等數學教學模式對高等數學教學效果的影響，從而為尋求更加合理的教學模式，達到更好的教學目的提供了理論依據．對高等數學教學的效果具有一定的預見性，從而可以相應的對教學形態做出對應的調整，對高等數學的教學具有重大的指導意義．

參考文獻：

[1] Husken，Stagge．Recurrent neural networks for time series classication[J]．Neurocomputing，2003，50：223-235

[2] Li S，Li Y，Liu B．Model-free control of Lorenz chaos using an approximate optimal control strategy[J]．Commun Nonlinear Sci Numer Simul，2012，12（7）：4891-4900

[3] Li S，Li Y，Wang Z．A class of finite-time dual neural networks for solving quadratic programming problems and its k-winners- take-all application[J]．Neural Network，2013，39：27-39

[4] Liu Q，Wang J．Two k-winners-take-all networks with discontinuous activation functions[J]．Neural Networks，2008，21（2-3）：406-413

[5] Li S，Chen S，Liu B．Accelerating a recurrent neural network to finite-time convergence for solving time-varying Sylvester equation by using a sign-bi-power activation function[J]．Neural Process Letter，2013，37：189-205

[6] 陳明．MATLAB神經網絡原理與實例精解[M]．北京：清華大學出版社，2013

[7] 許春根，楊孝平，趙培標，等．加強高等數學課程建設提高人才培養質量[J]．中國大學教學，2009（4）：43-45

[8] Miao Peng，Shen Yanjun，Xia Xiaohua．Finite time dual neural networks with a tunable activation function for solving quadratic programming problems and its application[J]．Neurocomputing，2014，143：80-89

[9] Miao Peng，Shen Yanjun，Huang Yuehua，et al．Solving time-varying quadratic programs based on finite-time Zhang neural networks and their application to robot tracking[J]．Neural Computing and Application，2015，26（3）：693-703

[10] Shen Yanjun，Miao Peng，Huang Yuehua，et al．Finite-time stability and its application for solving time-varying Sylvester equation by recurrent neural network[J]．Neural Process Lett，2015，42（3）：763-784

[11] Miao Peng，Shen Yanjun，Hou Jianshu，et al．A recurrent neural network with a tunable activation function for solving K-Winners-Take-All[C]//Proceedings of the 33rd Chinese Control Conference，Nanjing，2014：4957-4962

[12] 蘇德礦．高等數學教學如何與中學數學內容及教學方法有效地銜接[J]．中國大學教學，2013（5）：47-49

[13] 王鵬．論數學建模在數學教學中對應用型本科人才培養的作用[J]．高等教育，2011（11）：34

Analysis higher mathematics teaching mode based on discrete Hopfield neural network

MIAO Peng1，FAN Liu-jun2

（1. Department of Basic Course，2. School of Civil Engineering and Architecture，Zhengzhou College of Science and Technology，Zhengzhou 450064，China）

Based on the discrete Hopfield neural network，studies the teaching mode of higher mathematics，seeks a more reasonable teaching mode and achieves better teaching purpose．The abstract teaching is translated into the computer language．Then，design a discrete Hopfield neural network and analyze several existing advanced mathematics teaching mode．The given instance is solved by using the established discrete Hopfield neural network．The summary of the article is given and a reference for later higher mathematics teaching is provided．

discrete Hopfield neural network；higher mathematics；teaching model；instance simulation

1007-9831（2016）10-0055-03

O13∶G642.0

A

10.3969/j.issn.1007-9831.2016.10.016

2016-08-11

2016年度河南省社科聯、河南省經團聯調研課題項目（SKL-2016-3868）

苗鵬（1988-），男，河南鄭州人，助教，碩士，從事神經網絡優化、非線性系統穩定方面的研究．E-mail：miaopeng881026@163.com