數學思想——數學解題的靈魂——例說數學思想在數列解題中的運用

江蘇省徐州市銅山區大許中學　劉　影

數學思想——數學解題的靈魂——例說數學思想在數列解題中的運用

江蘇省徐州市銅山區大許中學劉影

數列是中學數學的重要組成部分，數列中的相當一大部分問題都可以體現數學的重要思想方法去處理。比如，數列中的基本量的確定可以依賴方程，把數列看成特殊的函數，可以借助于函數的思想方法研究，探究性的問題可借助于特殊化和賦值的方法。因此，以重要的思想方法來指導數列解題顯得尤為重要，本文就數學思想方法在數列中的應用，舉例說明。

數列；數學思想

一、方程的思想

例1公差不為零的等差數列｛an｝的前n項和為Sn。若a4是a3與a7的等比中項，S8=32，則S10=________。

解析：由a4=a3a7得

（a1+3d）2=（a1+2d）（a1+6d）得

2a1+7d=8，則d=2，a1=-3，

答案：60。

【評注：函數、方程、不等式是一個整體，知道其中任何一個，都可以往其他兩個轉化，數列中的方程思想主要是是利用數列中的基本量來確定數列，進而可以明確數列的通項和前n項和的表達式來處理問題。】

二、特殊化思想

例2等差數列｛an｝中，公差d＞0，前n項和為Sn，a2·a3=45，a1+a5=18。

（1）求數列｛an｝的通項公式；

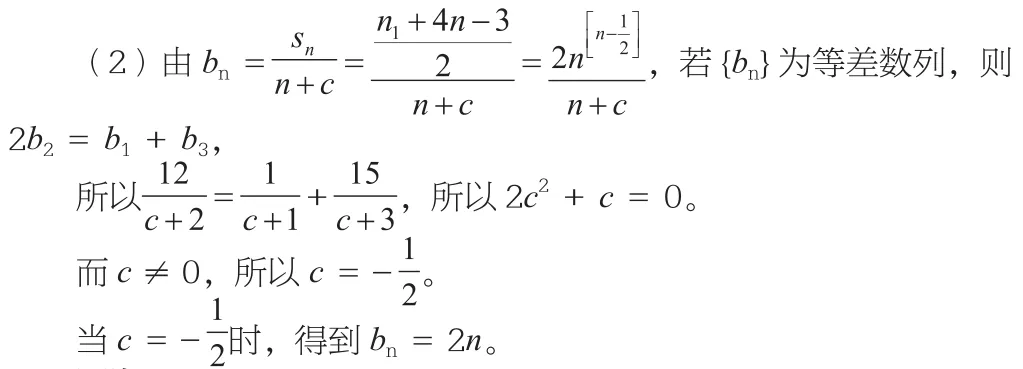
因為bn+1-bn=2（n+1）-2n=2（n∈N＊），

所以數列｛bn｝是公差為2的等差數列。

【評注：存在型探索性問題，是指判斷在某些確定條件下的某一數學對象（數值、圖形、函數等）不確定的問題。這類問題常常出現在“是否存在”“是否有”等形式的疑問句中，以示結論有待于確定。解答此類問題的思路是：通常假設題中的數學對象存在（或結論成立）進行特殊化，然后在這個前提下進行邏輯推理，找到命題成立的必要條件，進而進行充分性的論證。……