化歸方法在高中數學教學中的運用

江蘇省海門市能仁中學　馬　麗

化歸方法在高中數學教學中的運用

江蘇省海門市能仁中學馬麗

在解決高中數學問題時，可以采用某種方法將問題等價轉換為新的簡單化的問題，如函數y=x6+x3+k，可以等價轉換為y=a2+a+k（a=x3），將六次函數簡化為二次函數，這就是簡單的化歸的解題方法。通常化歸方法解題是將陌生問題熟知化，繁雜問題簡易化，抽象問題直觀化。

一、數與數之間的化歸

我們在高中數學中常用的換元法就是一種數與數之間的化歸。換元法解題的關鍵在于問題有相同的數學結構特征（即方程式、不等式、函數式等中的代數式），將相同的數學結構特征適當變換為一個新的變量，這樣就能夠將原始問題化難為易、刪繁就簡，實現問題的化歸。因此，解決這類問題需要培養學生注意分析問題的相同的數學結構特征，對已知函數中的代數式進行適當變形，洞察題目中的特殊數學結構，利用這些特殊數學結構進行代換。

求證：m1+m2+m3=m1m2m3。

【分析】學生往往采用求證的等式左邊通分化簡，右邊乘積化簡，然后讓結果相同而達到證明。雖然這種計算化簡在理論上是可行的，在實際計算中卻是“工程浩大”。我們可以采用將已知條件進行變形，然后通過數與數之間的化歸，走出一條捷徑。

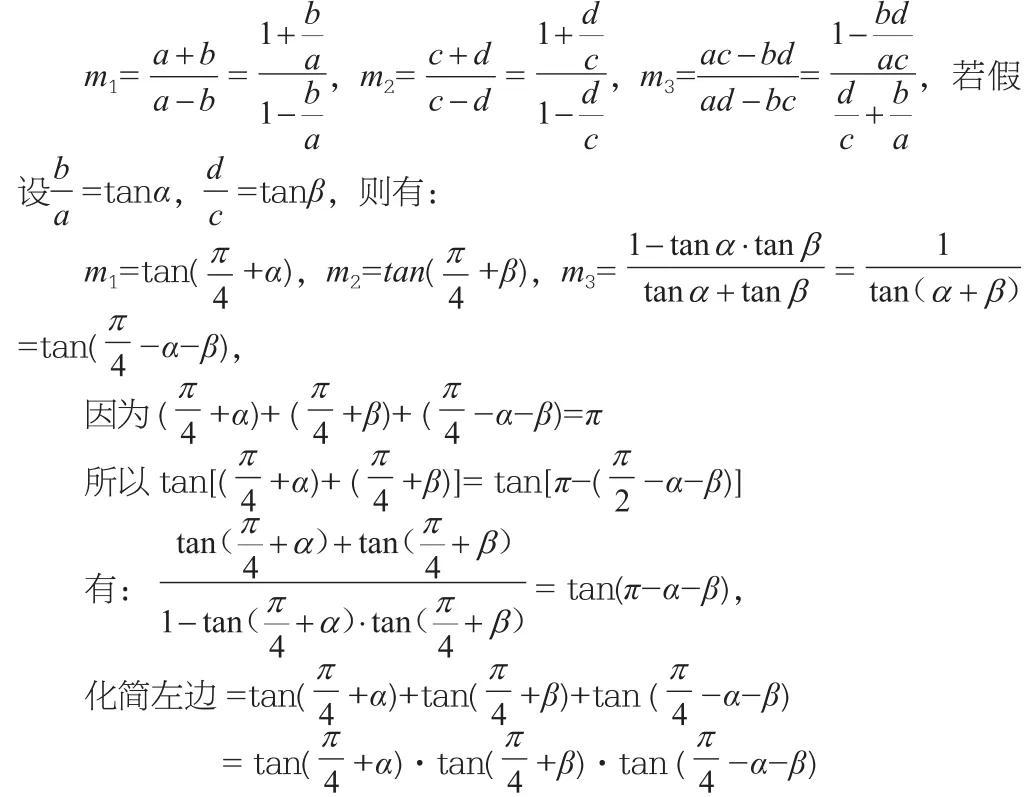
故等式成立。

數與數之間的化歸最關鍵的地方在于將陌生問題化歸為熟知，在應用我已有的知識或經驗將代數式變形代換，轉換為簡易的算式進行運算，從而達到解題的目的。……