基于QPSO算法的冷鏈物流配送運輸問題的研究

高曉巍

基于QPSO算法的冷鏈物流配送運輸問題的研究

高曉巍

隨著中國消費者生活模式的轉變，冷鏈產品的銷售比重迅速加大，優化冷鏈物流運輸路徑成為提高企業競爭力的關鍵。文章以物流運輸成本最小化與顧客滿意程度最大化為目標，利用QPSO算法進行求解。仿真實驗結果表明，QPSO算法在求解多配置中心多車輛的冷鏈物流運輸路徑問題中呈現出了較好的穩定性與收斂速度。

量子行為粒子群算法；冷鏈物流；客戶滿意度

一、引言

隨著現代化制冷技術的發展，海、陸、空運輸網絡的建立，人們對生鮮冷凍食品的品質和安全提出了更高的要求，這為冷鏈物流的發展提供了有力的契機。冷鏈物流是指以保證易腐食品品質為目的，以保持低溫環境為核心，以現代化制冷技術為手段的物流信息管理和配送系統。然而我國冷鏈物流的發展起步較晚，在物流設施、冷藏技術設備及配送管理等方面與歐、美、日發達國家差距較大。據不完全統計，我國每年由于冷鏈物流問題所帶來的經濟損失高達100億美元。因此，優化配送運輸路徑成為降低社會經濟損失，提高企業經濟效益的有效途徑之一。

二、文獻綜述

物流配送運輸路徑優化方法主要包括精確算法和群體智能算法兩種。由于群體智能算法的并行性、分布式、易操作性等特點使得遺傳算法、粒子群、蟻群等典型的群體智能算法在冷鏈物流研究中得到廣泛的應用。劉鎮等人在考慮多源實時交通信息的基礎上建立了運輸成本和配送時間的優化模型，并在云計算環境下利用粗粒度并行遺傳算法對模型假設進行了有效性的驗證；陶榮綜合考慮配送、貨損與懲罰三個主要成本要素建立了帶有時間窗的優化配送運輸模型，并通過蟻群算法驗證了模型的有效性和可行性。他所提出的多溫共配思想為冷鏈物流的發展注入了新鮮血液；量子粒子群（QPSO）優化算法是在粒子群（PSO）優化算法的基礎上，從量子力學的角度提出的一種新型算法。QPSO算法通過建立δ勢阱模型使處于量子束縛態的粒子按照一定的概率密度實現全局收斂，已經證實QPSO算法克服了PSO算法因速度限制搜索空間受限的問題。本文采用量子粒子群優化算法實現模型假設的驗證。

三、冷鏈產品物流配送路徑優化模型

冷鏈產品物流配送路徑優化問題可描述為在一定范圍內和約束條件下，將冷鏈產品通過儲運的方式實現在多個配送中心與供給客戶之間的空間位移，并使目標函數達到最優化。

假設冷鏈產品的配送中心有M個，運輸車輛有P輛（載重量均為r），客戶有N個（貨物需求為ni其中i=1，2，…，N），且每輛運輸車完成任務后均返回配送中心。客戶與配送中心的編碼分別為1，2，…，N，N+1，N+2，...，N+M；變量定義如下：

其中客戶在［Bi，Li］內的意度為1，在該區間以外客戶的滿意度隨時間ti而線性減少，α，β是客戶對時間的敏感系數。

冷鏈產品的儲運直接影響產品的質量與安全，因此，需同時考慮物流運輸路徑最短和客戶滿意程度兩個最優化問題，構建數學建模如下：

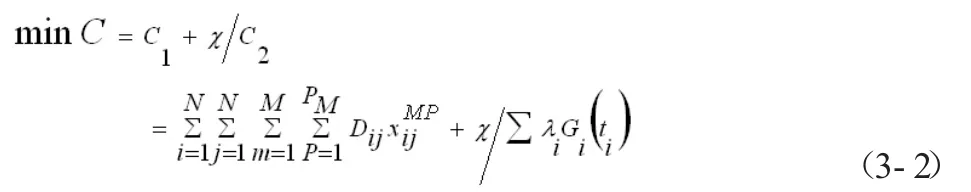
其中Dij表示兩個客戶i，j之間的距離；配送中心M具有PM輛儲運貨車。

目標函數需滿足如下約束條件：

（1）參與儲運的車輛不能超出配送中心的總車輛數，即

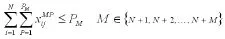
（2）參與儲運的車輛的承載數量是有限的，約束如下：

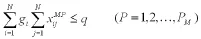
（3）每個客戶配送服務僅一次

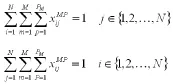
（4）配送路徑無子回路

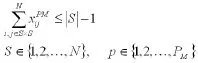
在目標函數中引入罰函數以約束車輛容量，

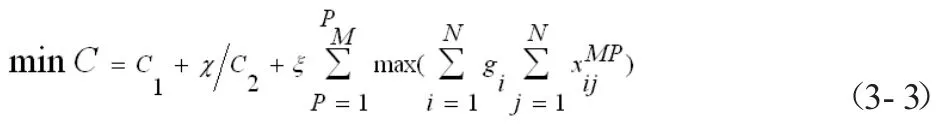
其中ξ取值足夠大時不可行解在迭代過程中將被淘汰。

四、基于QPSO算法的物流運輸路徑優化問題

（一）QPSO算法

QPSO算法從量子力學理論出發，通過建立δ勢阱模型束縛粒子，在收索空間中受量子束縛的粒子以一定的概率密度分布，當粒子與中心的距離趨于無窮大時，其概率密度趨于零。

在一個M維的目標搜索空間中，由N個粒子組成的種群的決策變量為粒子第t次迭代的位置向量，粒子個體最好位置為以最小優化問題minf（x）為例，由下式確定：

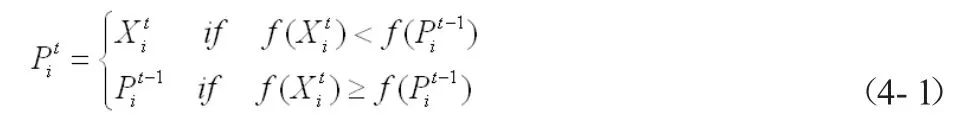
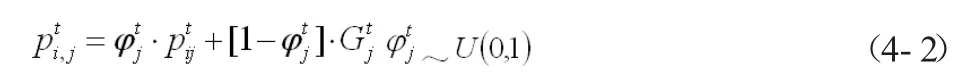
粒子的演化方程

當參數γ由1.0線性遞減到0.5時效果較好。

（二）粒子編碼

構造X1與X2兩個N維子向量。X1為車輛信息，X1∈［1，p］，X2為車輛儲運路徑信息。假設2個配送中心，對12個客戶進行儲運服務，每個配送中心所擁有的車輛數分別為2，3，且這5輛車的編碼分別為1至6。

表1　粒子編碼

儲運路線為：

配送中心1

車輛1的儲運路徑為：4→7

車輛2的儲運路徑為：10→11→8

配送中心2

車輛3的儲運路徑為：1→3

車輛4的儲運路徑為：12→9

車輛5的儲運路徑為：2→3→6

（三）基于QPSO算法的物流運輸路徑規劃算法

QPSO算法流程如下：

第一步：取種群規模為N，最大迭代次數T，對粒子進行編碼；

第三步：利用公式（4-3）計算平均最好位置；

第七步：轉第三步繼續迭代，達到迭代次T結束；

（四）仿真實驗結果與分析

假設某地由3個配送中心對該地區的15個門店提供儲運服務，每個配送中心1，2，3的車輛數分別為2，2，2，6輛車的編碼分別為1，2，……，6；14個客戶及3個配送中心在XOY平面的位置信息如下表2，表3所示

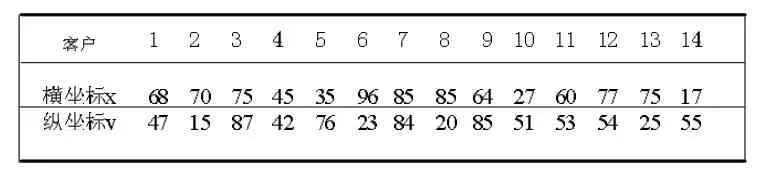
表2　客戶信息

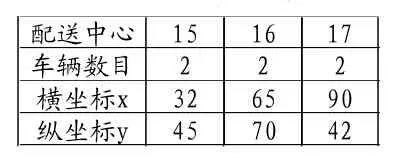
表3　配送中心信息

通過Matlab7.0對QPSO算法進行計算機仿真實驗。結果表明了QPSO算法的可行性和有效性。儲運路線如圖1所示。

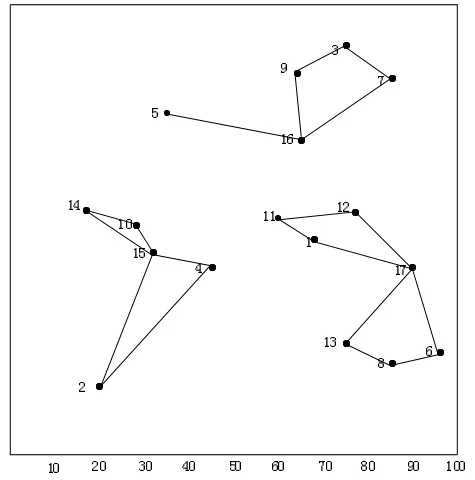
圖1　最優配送方案圖

經粒子解碼得到有效路徑為：

配送中心1的車輛1：15→10→14→15

配送中心1的車輛2：15→4→2→15

配送中心2的車輛3：16→5→16

配送中心2的車輛4：16→9→3→7→16

配送中心3的車輛5：17→12→11→1→17

配送中心3的車輛6：17→13→8→6→17

仿真實驗結果如下：

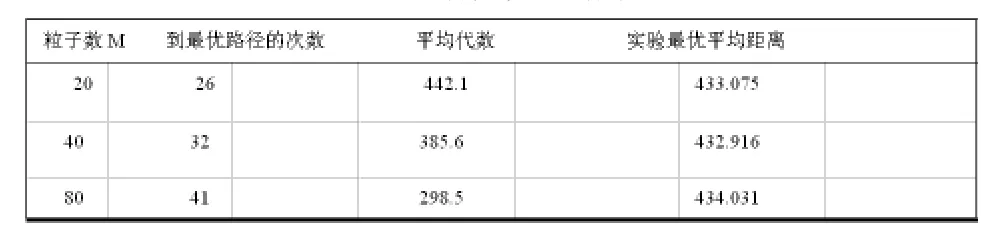
表4　仿真實驗結果

由上表可見QPSO算法在解決冷鏈產品物流儲運路徑問題中呈現出較強的穩定性與收斂性。

五、結束語

隨著中國消費者對冷鏈產品需求量的增加及對產品質量安全性的重視，為冷鏈物流的發展提供了機遇，研究冷鏈產品的儲運優化路徑，是提高物流企業競爭力及消費者滿意度的關鍵。本文從現代物流管理理念出發，以冷鏈產品的儲運成本最小化與顧客的滿意程度最大化作為優化目標，使得算法的研究與實現更具有現實意義。

［1］方凱，鐘漲寶，王厚俊.賀嵐基于綠色供應鏈的我國冷鏈物流企業效率分析［J］.農業技術經濟，2014，（03）：50-53.

［2］邵瑞銀.河南省農產品冷鏈物流現狀、問題與對策［J］.企業經濟，2013，（02）：15-17.

［3］劉鎮，徐優香，王譯.基于云計算的冷鏈物流配送車輛路徑優化方法研究［J］.電子設計工程，2013，（04）：23-27.

［4］陶榮.基于蟻群算法的多溫共配冷鏈物流配送問題研究［J］.物流技術，2014，（02）：31-34.

［5］孫俊.量子行為粒子群優化 ［M］.北京：清華大學出版社，2011，8.

［6］張仁堂，董海洲，喬旭光等.現代果蔬物流中冷鏈技術集成創新研究［J］.世界農業，2007，9（3）:47—49.

高曉巍，女，黑龍江齊齊哈爾人，齊齊哈爾大學理學院副教授，研究方向：智能規劃、優化算法。

N945.12

A

1008-4428（2016）10-12-03