為學習設計教學：教學設計最根本的著力點*——以“函數的概念”的教學設計為例

☉江蘇省鹽城中學　劉海濱

為學習設計教學：教學設計最根本的著力點*——以“函數的概念”的教學設計為例

☉江蘇省鹽城中學劉海濱

一、教材分析

函數概念是中學數學中最重要的核心概念之一，函數的思想和方法貫穿高中數學課程的始終，學會用函數的觀點和方法解決數學問題，是高中數學主要的學習任務之一.然而，函數概念因其取元的任意性、成象的唯一性及對應法則“f”的高度抽象性，而成為最難把握的概念之一，無論是教師的教還是學生的學，都存在很大困難.因此，如何全面而深刻地理解函數概念、破解概念教學難點是學好函數概念的根本所在.

從教的角度看，函數概念教學的核心是引導學生開展概括活動：將凝結在數學概念中的數學思維活動打開，以若干典型具體事例為載體，引導學生展開分析各事例的屬性、抽象概括共同本質屬性、歸納得出數學概念等思維活動而獲得概念.數學教學要“講背景，講思想，講應用”，概念教學則要強調讓學生經歷概念的概括過程.

從學的角度看，概念形成和概念同化是兩種基本的概念獲得方式.概念形成的實質是抽象出一類對象的共同本質屬性的過程，其思維活動的核心是概括；概念同化就是學生利用已有認知結構中的相關知識理解新概念，理解的過程是新舊知識的相互作用過程，是將新知識納入已有認知結構的過程，思維活動的核心仍是概括.

二、教學流程

1.復習回顧，點擊課題

教師：在初中，我們是如何定義函數的？學習了哪些函數？

學生：對于一個變化過程中的兩個變量x，y，若對于任意一個值x，都有唯一值y與之對應，則稱y是x的函數，其中x叫作自變量.學過了正比例函數、反比例函數、一次函數、二次函數.

設計意圖：通過舉例回顧，強調“單值對應”，思考題是為了激發學生的學習動機.

2.探索實例，建構模型

教師：今天我們來進一步從其他角度學習函數的概念.（板書課題）

實例一：一枚炮彈發射后，經過26s落到地面擊中目標.炮彈的射高為845m，且炮彈距地面的高度h（單位：m）隨時間t（單位：s）變化的規律是h=130t-5t2.

問題1：炮彈飛行1s，5s，13s，30s時離地面的高度？

問題2：變量t和h的取值范圍是多少？用集合表示.

問題3：對于數集A的任意一個時間t，按照變化規律，在數集B中是否都有唯一確定的高度h和它對應.

實例二：圖1中的曲線顯示了南極上空臭氧層空洞的面積從1979～2001年的變化情況.

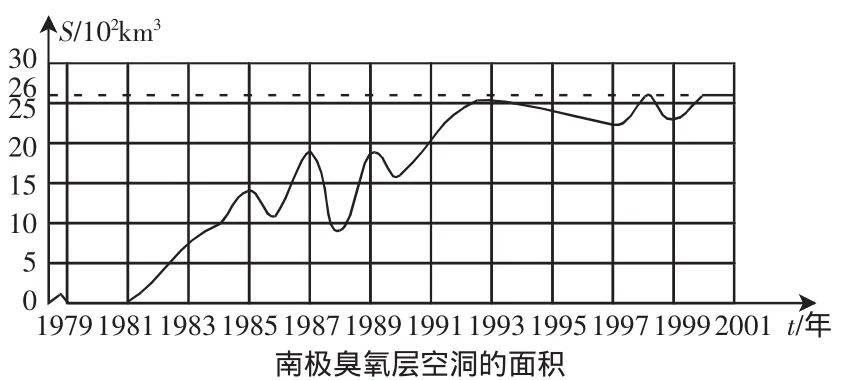
圖1　

問題4：曲線中，哪一年空洞面積S最大？S=1500萬平方千米的年份有哪些？

問題5：t和S的取值范圍是什么？用集合表示.

問題6：對于數集A中的每一個時刻t，按照曲線，在數集B中是否都有唯一確定的臭氧層空洞面積S和它對應.

實例三：表中恩格爾系數隨時間（年）變化的情況表明，“八五”計劃以來，我國城鎮居民的生活質量發生了顯著變化.

時間1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001恩格爾系數53.852.950.149.949.948.646.444.541.939.237.9

問題7：系數y與時間x之間的關系是否和前面兩例中的變量之間的關系相似？

問題8：仿照前面兩個實例來描述這個關系？

設計意圖：進一步體會函數是兩個變量之間的函數模型.

3.歸納共性，形成概念

教師：以上三個實例有什么共同點？

學生：在集合A中每取一個數，按照一定的對應關系，在集合B中都有唯一的一個數與之對應.

教師：如果我們把A中的數記為x，集合B中的數記為y，對應關系記為f，那么我們又如何歸納上述三個例子的共同特征呢？

學生：對于數集A中的每一個x，按照某種對應關系f，在數集B中都有唯一確定的y和它對應.

教師補充：像這樣在對應關系f作用下集合A到集合B，我們記作：f：A→B，讀作：f，A到B.為此我們得到函數的概念：設A、B是非空數集，如果按照某種確定的對應關系f，使對于集合A中的任意一個數x，在集合B中都有唯一確定的數f（x）和它對應，那么稱f：A→B為從集合A到集合B的一個函數（function），記作：y=f（x），x∈A.其中，x叫自變量，x的取值范圍A叫作定義域（domain），與x值對應的y值叫函數值，函數值的集合C=｛f（x）|x∈A｝叫值域（range）.

教師：對于函數定義中的“f（x）”，我們該如何理解呢？可否理解成f與x的乘積呢？

學生活動（分組討論，代表回答）：f（x）只是表示函數符號，是集合A中取x時，按對應關系f，在集合B中的值.不能理解成f與x的乘積.

設計意圖：三個對應關系不同引導學生引進符號表示，體會對應關系在刻畫函數概念中的作用.

4.辨析概念，深化鞏固

教師：f（x）是否可以換成其他符號呢？

學生：因為f（x）只表示函數符號，f是表示對應關系的字母，也可用其他字母表示，如g表示對應關系，則g（x）就表示在集合A中取x時，按對應關系在集合B中的值.

學生（一名突然舉手的學生）：老師，“對應關系”是什么意思？

教師：通過前面實例，我們不妨可以這樣理解：把f看成一臺加工的機器，集合A是原料箱，集合B是產品箱，集合A中每給一個原料經過f機器加工就成B中的一件產品.例如h與變量t滿足的關系式h=130t-5t2，t每取一個值，按照這種對應關系，h都有唯一對應的值.

例1你能說說已學函數的定義域和值域嗎？（師生共同完成）

①一次函數f（x）=ax+b（a≠0）：定義域為R，值域為R；

②反比例函數（k≠0）：定義域為｛x|x≠0｝，值域為｛x|x≠0｝；

③二次函數f（x）=ax2+bx+c（a≠0）：定義域為R，值域：當a>0時

注：（1）函數的定義域通常由問題的實際背景確定，如我們剛開始所述的三個實例.如果只給出解析式y= f（x），而沒有指明它的定義域，那么函數的定義域就是指能使這個式子有意義的自變量的取值集合.（2）函數的定義域和值域用集合表示.

例2（幻燈片展示）下列哪些表示集合A到集合B的函數？若不是，說明理由.

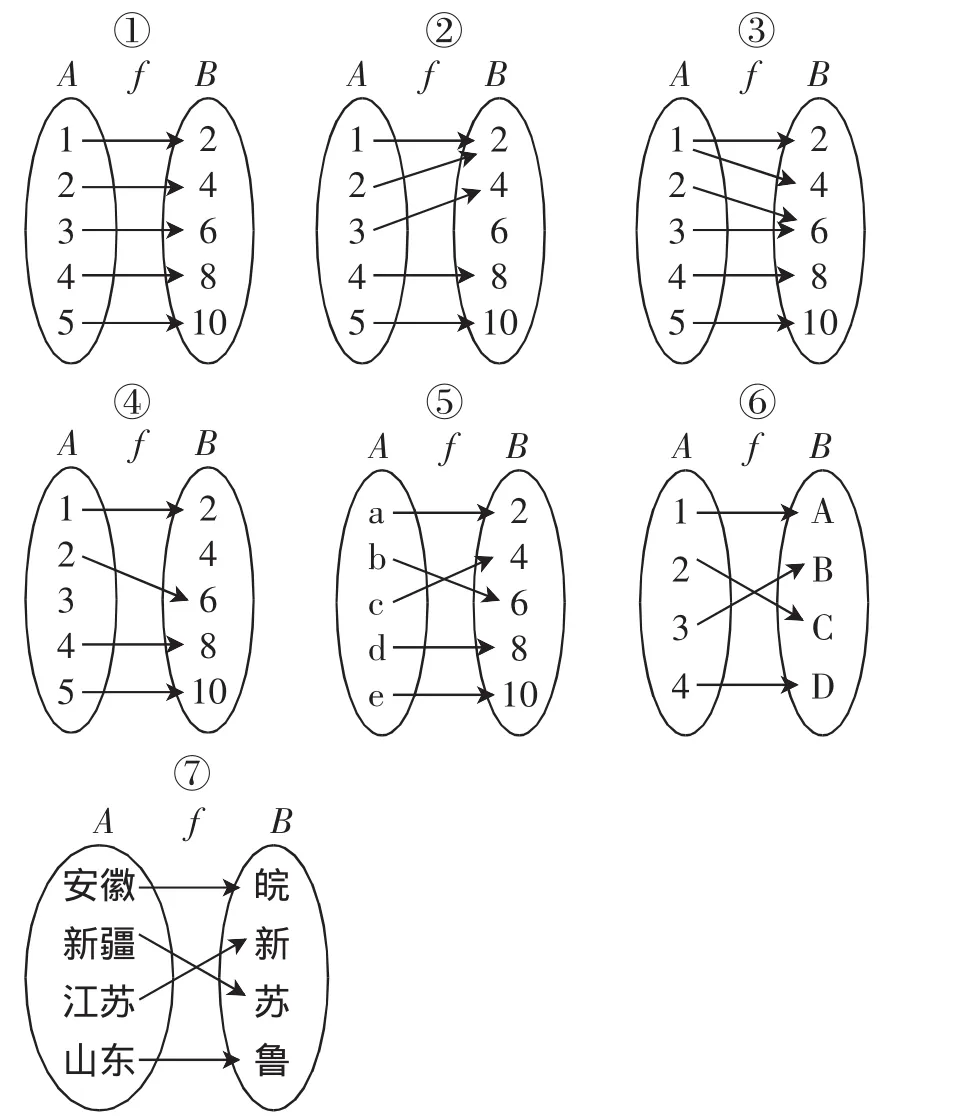
學生1：①是；②也是函數.

教師追問：②為什么是函數呢？在集合A中沒有數與集合B中的6對應呀？

學生1遲疑后回答：因為函數的定義是如果按照某種確定的對應關系f，使對于集合A中的任意一個數x，在集合B中都有唯一確定的數和它對應.本題滿足函數的定義.

教師追問：也就是說集合B中可以有元素剩余了？

學生1：是.

教師借此機會把剛才板書的函數定義中“值域是集合B的子集”進行解釋.

教師強調：像①中的對應關系，我們就可以理解為集合A中數的2倍等于集合B中的數；②中也存在著一種對應關系，只是我們找不出具體的對應關系的式子.

學生2：③④都不能表示函數關系；因為③的A集合中的數1在集合B中有2與4兩個數與之對應，不滿足函數定義；④的A集合中的數3在集合B中沒有數與之對應，不滿足函數定義.

教師：很好.所以在剛才給出函數定義時，自變量的取值集合就是A，我們稱作函數的定義域.⑤⑥⑦找一名同學回答.

學生3：都是（教師疑惑）

學生4：⑤⑥是，⑦不是.

教師：為什么？

學生4：因為⑦的兩個集合中元素都是省名和省的簡稱，故不滿足函數概念.

教師提出：不錯，基本上說到實質上了.⑤⑥是嗎？判斷是否為函數關系，主要看是否滿足函數定義.

學生5（在大家紛紛議論一會后舉手回答）：⑤⑥⑦都不是，因為函數定義中說A、B集合的元素必須是數，而⑤中集合A、⑥中集合B的元素都是字母，⑦中集合的元素都不是數.

教師：太棒了！（示意全班學生為學生5鼓掌）.請同學們再來看一下思考辨析，進一步來鞏固函數的概念.

設計意圖：用任意性和唯一性判斷，找對應法則，分析定義域值域，小結：從集合A到集合B的對應關系可以是一對一、多對一，不能是一對多.函數概念的核心本質：兩個數集A、B之間的一種單值對應關系：從自變量x的集合A到函數值y的集合C的一種對應關系.對于A中的任意一個元素，B中都有唯一的元素與之對應，即一對一、多對一；而B中的元素在A中的對應元素可以不唯一，也可以沒有，顯然B包含值域C，原因是：函數的三要素中值域是由定義域和對應關系決定的.

例3辨析下面語句的正誤.

（1）y=1（x∈R）是函數嗎？

學生：（1）是；（2）不是，因為當x=1時，y有兩個值；（3）是.

教師：若（3）是，請大家求一下它的定義域.（板書提示：由x-3≥0且1-x≥0來求x的取值集合）.

學生：空集.

教師追問：這樣還能是函數嗎？

學生：不能，因為函數定義中說A、B是兩個非空數集.

教師：這個問題大家終于看出來了.通過以上例子，大家討論一下，我們從中總結函數定義具有哪些特點？

學生回答不同情況以后，教師與學生共同總結，函數定義有以下特點：①A、B必須是非空數集（若是空集就沒有研究意義）；②集合A中不能有元素剩余，集合B中可以有元素剩余；③按對應關系只能一對一或多對一，但不能一對多；④集合A是函數的定義域，集合B包含函數的值域（或稱函數的值域是集合B的子集）；⑤f（x）表示每給一個自變量x，按照對應關系f，都對應確定一個函數值f（x），而不是f與x的乘積.

教師：函數的概念主要由哪幾部分構成？

學生：定義域、對應關系和值域.

教師：很好.我們把定義域、對應關系和值域稱為函數的三要素.

（1）求函數的定義域；

（3）當a>0時，求f（a），f（a-1）的值.

（學生板演，教師點評，具體解答略）

5.課堂小結，知識提煉

今天我們收獲是什么？（學生回答，教師點評）

（1）你對“函數是描述變量之間的依賴關系的數學模型”這句話有什么體會？

（2）對比初中和高中函數概念，你有什么發現？

設計意圖：反饋學生的當堂表現，了解知識掌握情況.

三、結束語

函數概念已成為現代數學的基本思想之一，是整個高中數學的核心概念，它滲透到了數學的一切領域.函數是數學知識體系的有力基礎，也是數學學習中最難掌握的概念之一.

數學發展史表明，函數概念從產生到完善，經歷了漫長而曲折的過程.這不但因為函數概念系統復雜、涉及因素眾多，更重要的是伴隨著函數概念的不斷發展，數學思維方式也發生了重要轉折：思維從靜止走向了運動、從離散走向了連續、從運算轉向了關系，實現了數與形的有機結合，在符號語言與圖、表語言之間可以靈活轉換.在函數的研究中，思維超越了形式邏輯的界限，進入了辯證邏輯思維.與常量數學相比，函數概念的抽象性更強、形式化程度更高.總之，概念的識別優于概念特征的說明，概念外延的掌握優于概念內涵的掌握.對概念內涵的掌握，取決于概念本質特征的多少及它們之間的關系.本質屬性越多越鮮明，概念形成越容易；非本質屬性越多越明顯，概念形成越難.對于所有概念，都是先掌握具體概念后掌握抽象概念，先掌握形式概念后掌握辯證概念.

*本文是江蘇省中小學教學研究室第九期課題《基于數學實驗室建構的高中數學實驗教學模式的研究》（編號：Jk9-L157）的研究成果之一.