一類歐式期權定價問題

荊卉婷

一類歐式期權定價問題

荊卉婷

賦權分數布朗運動因具備長程相依性、重對數率等精美性質，可用于資本市場。文章主要考慮由賦權分數布朗運動驅動的金融市場，從其相關性質出發，定義了新型的歐式期權定價公式并繪制出一些仿真結果。

賦權分數布朗運動；歐式期權

一、前言

具有長程相依性的自相似隨機過程廣泛應用于包括金融、電信學、流體力學 等許多領域。分數布朗運動(fractional Brownian motion)是使用最廣泛的一種，也是自相似高斯過程中唯一一個具有平穩增量的隨機過程。近年來，分數布朗運動以其簡單的結構、精美的性質以及廣泛的應用引起了許多學者的興趣，隨著研究的不斷深入，已經獲得了很多有意義的結果但是與分數布朗運動的廣泛研究相比較，其它類型的自相似高斯過程的研究卻非常少！這主要是由于其他類型自相似高斯過程并沒有平穩增量，且相依結構更為復雜。

此后，很多學者開始了諸如次分數布朗運動，雙分數布朗運動等自相似高斯過程的研究，然而對于賦權分數布朗運動的研究還非常少，結構也更加復雜，這也是我們開展賦權分數布朗運動研究的原因之一。另一方面，賦權分數布朗運動涵蓋分數布朗運動、雙分數布朗運動等許多具有長程相依性的自相似高斯過程，所以我們認為這類研究對于金融市場的定價問題具有應用意義。

本文主要研究賦權分數布朗運動在金融市場中的一個應用，給出了由賦權分數布朗運動版本的歐式期權定價公式，并繪出了當長程相依性指數及波動率取不同值時，歐式期權的價格隨時間變化的圖像。

二、歐式期權定價公式及相關證明

由于金融系統的復雜性，投資者往往不是在得到金融信息時立刻做出決定，而是等信息達到一定的量的時候再做出決定。這種行為往往導致長程相依性，賦權分數布朗運動能夠成為解釋這種現象的有用工具。在我們的模型中，假設股票價格V服從下面的隨機過程：

假設金融市場有兩種資產，其中一種資產為證券，收益率為無風險利率r;另一種資產為股票，其收益率是一個隨機過程Vt，初始價格為V0。我們關心的是以此股票為標的資產的到期日為T執行價格為k的歐式期權定價問題。

定義1：股票價格{Vt}的預期收益μ與時間T之間滿足

因為對{Vt}沒有限制，μ一般情況下與T有關。

引理1：歐式看漲期權價格C(K,T)為

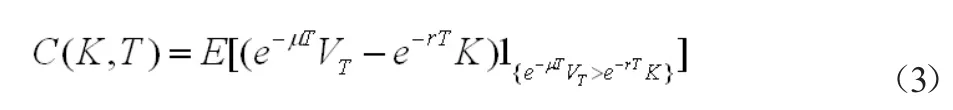
類似的，歐式看跌期權價格P(K,T)為

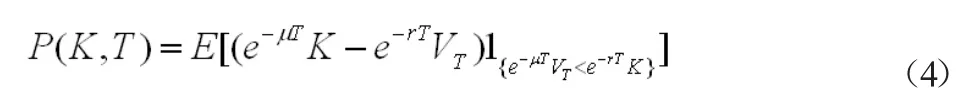
因此我們有

引理2：方程（1）的解為

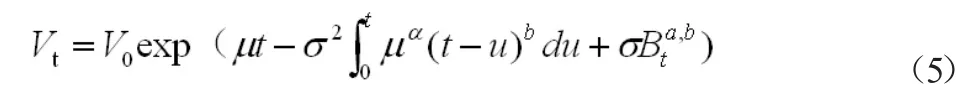
定理1.到期日為T執行價格為K的歐式看漲期權價格C(K,T)為

其中

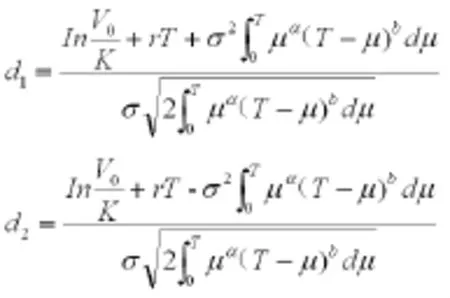
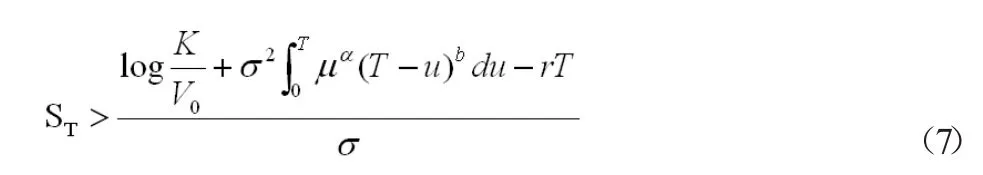
又根據引理（1）（2），可知到期日執行價格為的歐式期權價格C（K,T）為

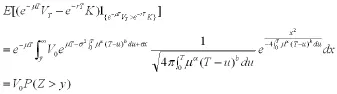
另一方面，我們可以類似證明.

三、數值仿真

根據以上內容，給出一些數值仿真結果，在圖（1）～圖（4）中，我們繪出了不同參數值σ∈{0.2，0.3,0.5}從圖可以看出，看漲期權的價格是到期日T，波動率σ及長相依指數α的增函數；看跌期權的價格是波動率σ及及長相依指數α的增函數，但關于到期日T是先增后減。取σ∈{0.2，0.0，0.2}固定b=0.4的圖像

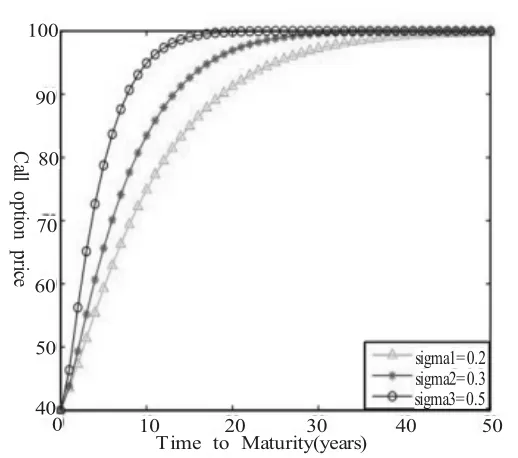
圖（1）

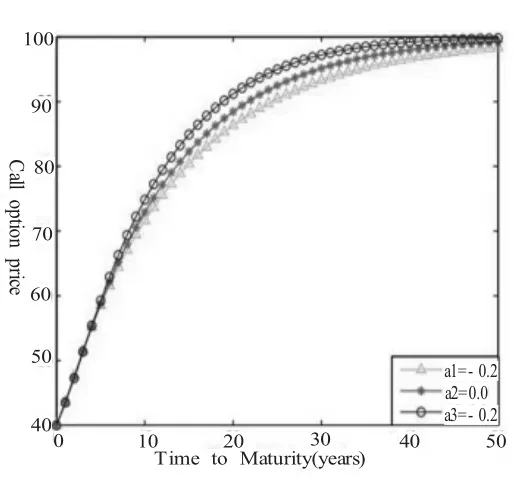
圖（2）

圖（1）：期權價格關于到期日為T的圖像，其中的參數值為r=0.06，α=0.2，b=0.4，K=60，V0=100,0＜T＜50.

圖（2）：期權價格關于到期日為T的圖像，其中的參數值為b=0.4， r=0.06，σ=0.2，K=60，V0=100,0＜T＜50.K=60，V0=100,0＜T＜50.

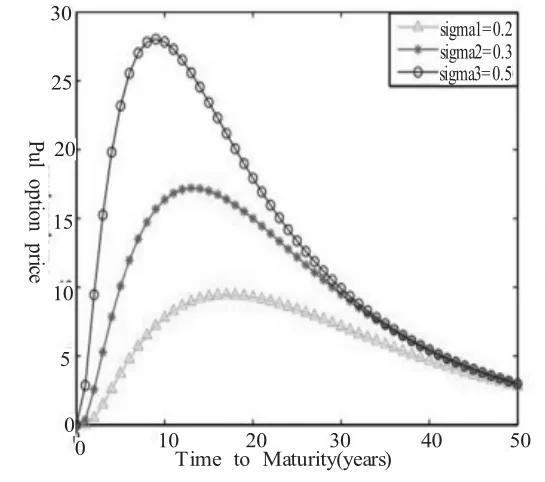
圖（3）

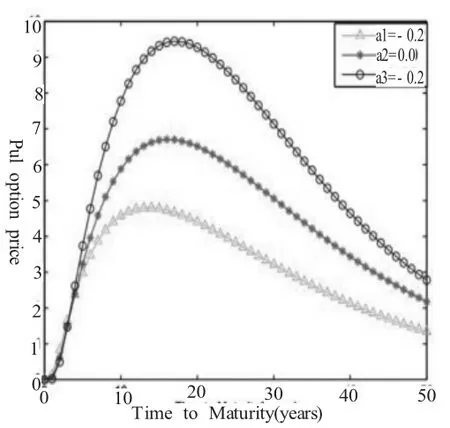
圖（4）

圖（3）:長程相依指數取不同參數值時歐式看漲（看跌）期權價格關于到期日T的圖像，其中的參數數值為r=0.06，α=0.2，b=0.4，K=60，V0=100,0＜T＜50.

圖4：長程相依指數取不同參數值時歐式看漲（看跌）期權價格關于到期日T的圖像，其中的參數數值為b=0.4，r=0.06，σ=0. 2，K=60，V0=100,0＜T＜50.K=60，V0=100,0＜T＜50.

四、總結

本文利用賦權分數布朗運動的一些良好的性質與實際金融市場相結合，建立了依托該理論的數學公式，試利用其特質給出歐式期權的定價公式，并繪制了仿真圖像，發現賦權分數布朗運動，確實可應用于金融市場，尤其是在信用違約率、期權定價等方面擁有廣泛應用，因此未來進行更優化處理會得到更準確的結論，并且非常具有實用價值。

[1]E.Al′os,O.Mazet and D.Nualart,Stochastic calculus with respect to Gaussian processes,Ann.Prob.29(2001),766-801.

[2]L.An and L.Yan,Smoothness for the collision local time of fractional Brownian motion,Preprint,2011.

[3]Yan L,Yang X.Some Remarks on Local Time-Space Calculus. Stat Prob Lett,2007,77:1600-1607.

[4]安磊.賦權分數布朗運動的軌道分析[D].東華大學，2011.

荊卉婷，女，黑龍江佳木斯人，寧波工程學院經濟與管理學院助教、碩士，研究方向：金融工程。

F830.91

A

1008-4428（2016）06-79-02