軌道扣件彈性墊板結構優化設計

朱泓吉+卜繼玲+王永冠+龍騰蛟

摘要： 采用OptiStruct對某型鐵路扣件軌下墊板進行拓撲優化和自由形狀優化，實現墊板結構輕量化設計.根據優化空間最大化原則，對垂向載荷工況進行拓撲優化、對極限載荷工況進行自由形狀優化.使用Abaqus極限載荷扣件系統仿真模型對優化后墊板結構性能進行驗證評價.結果表明：優化后的墊板性能基本不變，質量減少約10%，剛度滿足設計要求.優化結果可為墊板輕量化設計提供參考.

關鍵詞： 軌道； 彈性墊板； 輕量化設計； 結構優化； 拓撲優化； 自由形狀優化

中圖分類號： U213.532； TH122 文獻標志碼： B

0 引 言

隨著我國鐵路運輸的發展，車輛軸重的增加對軌道結構的影響越來越突出，輪軌間的動態效應對軌下基礎的破壞越來越明顯，線路養護和維修更加頻繁，軌道扣件彈性支撐層對軌道平順性的保護也變得越來越重要.本文利用虛擬仿真技術，對某型鐵路扣件軌下彈性墊板的結構進行優化研究，在保證墊板性能的前提下，通過對墊板結構的優化設計，改善墊板結構受力，減少墊板使用材料，提高安全效益和經濟效益，為軌下墊板輕量化設計提供參考.

1 墊板有限元建模和靜態特性分析

1.1 有限元模型建立

扣件系統由多個零部件組裝而成，其作用是固定鋼軌在正確位置，防止鋼軌的橫向和縱向位移，防止鋼軌傾翻，提供適量的彈性并將鋼軌所受的力傳遞給軌枕或道床承軌臺.[1]在建立扣件有限元模型時，適當簡化模型以減輕工作量，方便優化計算.利用HyperMesh進行網格劃分，其中墊板使用材料為熱塑性彈性體，材料參數擬合后呈線彈性.因此，采用8節點線性六面體單元C3D8模擬，網格數量為787 424個.1/4有限元模型見圖1.

1.2 邊界條件及材料屬性

在有限元分析中，將上工裝上表面節點與載荷施加點用RBE2單元進行連接，固定下工裝和上工裝橫向自由度，在載荷施加點施加載荷F.在靜剛度試驗中，墊板計算結果取加載0～100 kN垂向載荷時20～90 kN的割線剛度作為彈性墊板靜剛度.由于載荷和邊界條件的對稱性，只取模型的1/4進行仿真計算，x與z兩平面對稱，底面固定約束，施加垂向載荷22.5 kN，見圖2.

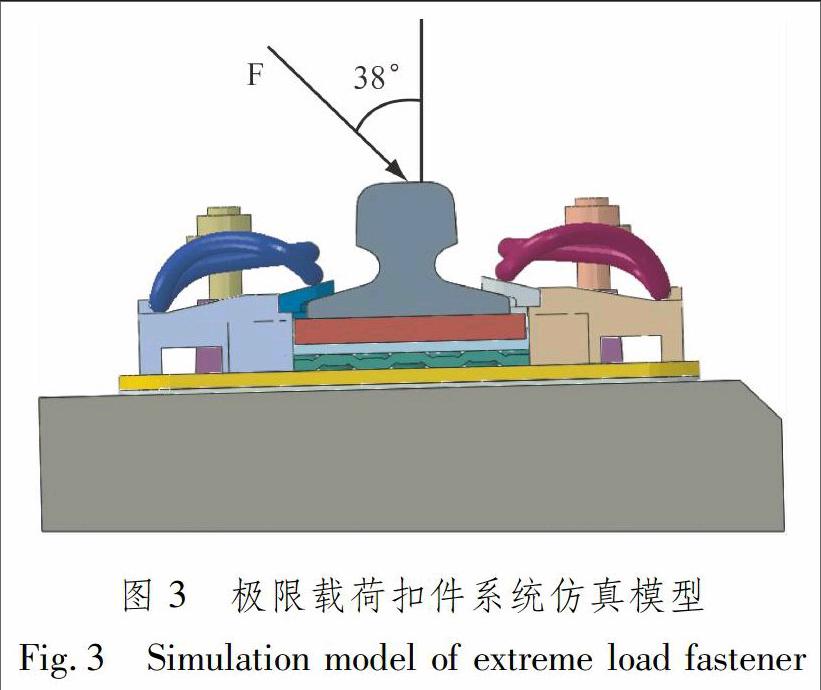
在極限疲勞載荷扣件系統中，墊板載荷方向與垂向成38°，大小為114 kN，即墊板承受90.00 kN垂向載荷和70.32 kN橫向載荷，根據對稱性，取扣件系統的1/2模型進行計算，底面固定約束，見圖3.

1.3 設計要求與結構分析

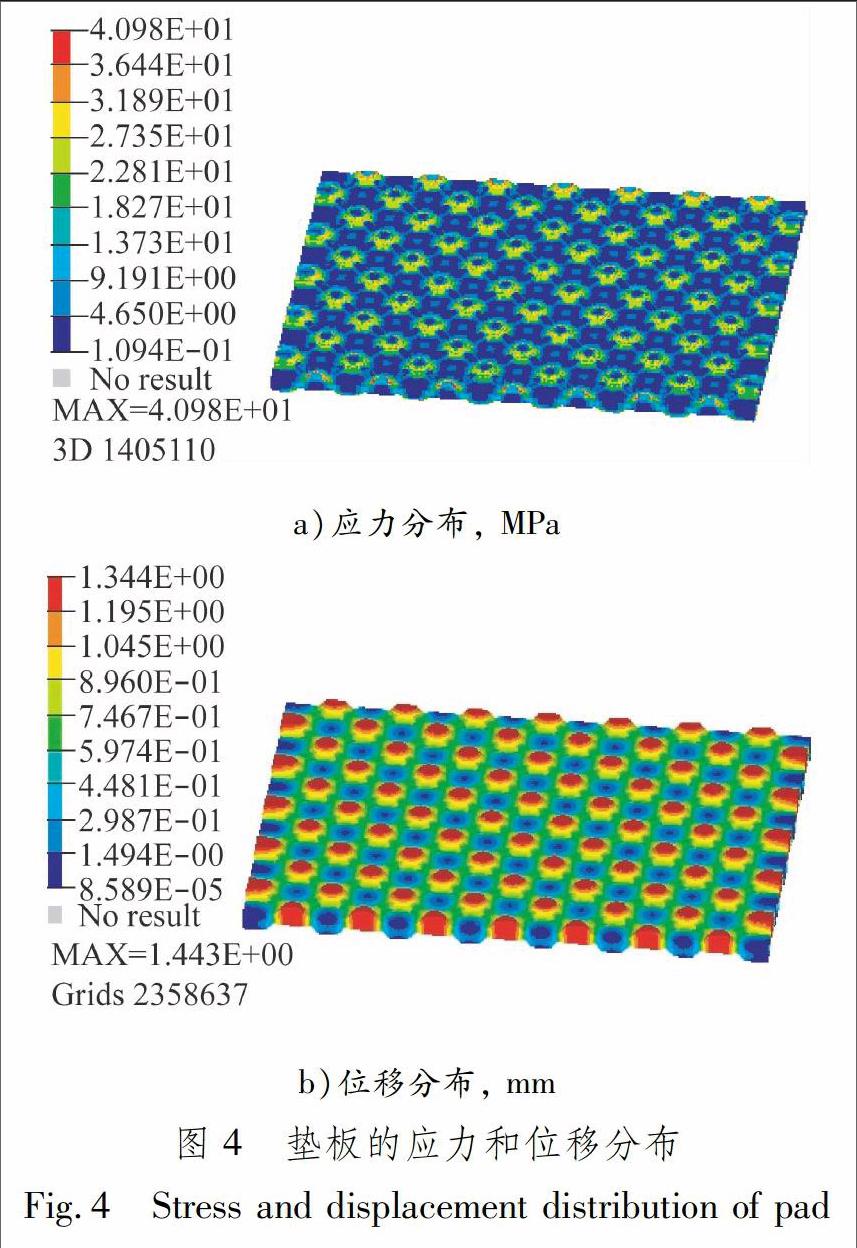
對原始墊板結構進行靜剛度仿真分析（90 kN垂向載荷），墊板的應力、位移分布見圖4.軌下彈性墊板的材料為某彈性體，靜剛度要求為50±10 kN/mm，而原始結構墊板靜剛度為66.91 kN/mm，最大應力40.98 MPa，體積約為6×104 mm3，靜剛度顯然不符合設計要求.由圖4可知，墊板受力不均勻，存在部分“不受力”區域，沒有實現等強度的設計理念，因此有必要對墊板進行結構改進使其滿足設計要求，減少制造材料，提高經濟效益.

2 優化分析

拓撲優化是設計域材料分布的優化.將有限元模型設計空間每個單元的單元密度（Density）作為設計變量，保留重要區域，從而實現輕量化設計.[2]在拓撲優化中，每個單元的密度值應取為0或1，單元分別定義為空或實體.[3]

形狀優化將設計空間分成若干控制區域，每個區域的形狀簡化為關鍵控制節點的位置.移動這些關鍵節點，邊界形狀產生變化，從而得到更為細致、合理的幾何形狀.[4-6]

基于輕量化目的，采用拓撲優化得到最佳的材料分布，結合自由形狀優化確定結構最優形面，在保證墊板承載性能的前提下，改善結構受力，減少使用墊板材料.[7]

2.1 拓撲優化

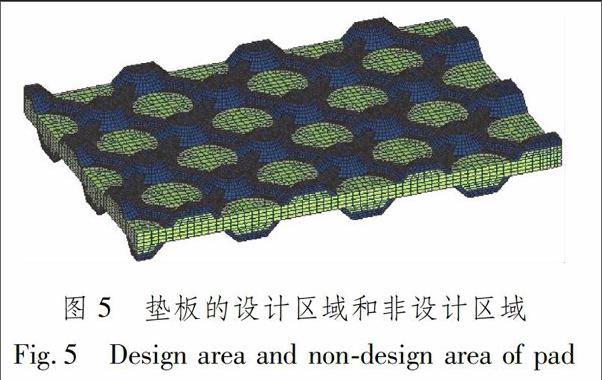
在進行拓撲優化前，首先要根據設計要求和結構特點定義結構的初始設計區域和非設計區域，然后根據結構所需要滿足的功能選擇合適的約束和目標函數.為盡可能利用現有模具、減少制造費用，選擇將凸臺作為非設計區域.加強筋拓撲優化沒有實質含義，因此不作為拓撲優化設計區域，后續的形狀優化也能影響加強筋的“存亡”.根據彈性墊板的結構特征、有限元分析結果及以上條件，在HyperMesh中將有限元網格分成設計區域（淺色）和非設計區域（深色），見圖5.

在結構拓撲優化中約束垂向位移，設計變量為單元密度，目標函數為墊板體積最小.設置好各項參數后提交OptiStruct對垂向載荷工況的墊板進行拓撲優化計算，優化后墊板的單元密度云圖見圖6.

拓撲優化后墊板靜剛度為57.69 kN/mm，最大應力為44.44 MPa，體積約為4.28×104 mm3.墊板最大應力稍有增大，靜剛度滿足設計要求，應力和位移分布見圖7.由于墊板在實際應用中會被置于極限載荷工況下，過多的去除材料會大幅降低墊板剛度，反而不能滿足工作要求，因此還要對極限載荷工況下的墊板凹槽和加強筋進行自由形狀優化.

2.2 自由形狀優化

自由形狀優化設計變量為凹槽和加強筋表面節點的線性擾動，設置位移約束、應力約束和對稱約束，目標函數為最小體積.經過6次迭代，形狀變化云圖見圖8.考慮到制造約束和制造成本，分別對加強筋尺寸和凹槽尺寸進行統一修正.自由形狀優化后墊板靜剛度為57.75 kN/mm，最大應力為40.52 MPa，體積約為5.4×104 mm3，自由形狀優化設計模型應力位移云圖見圖9.

2.3 優化結果對比

作為線彈性材料，熱塑性彈性體存在一定的塑性，但此處扣件系統中分析所得到的應力和應變數值僅為對結構優化前后提供對比而使用.將優化前后墊板模型置入Abaqus中建立極限載荷扣件系統仿真模型，得到優化前后墊板應力應變云圖見圖10和11.通過前述分析可知墊板優化前、后在極限載荷扣件系統中性能相近，見表1.由此可以看出：在相同性能下，優化設計模型體積較以前減輕約10%，靜剛度為57.75 kN/mm，滿足設計要求（50±10 kN/mm），達到輕量化目的.

3 結 論

通過分析校核—優化分析設計—再次分析校核的“循環式”方法對彈性墊板進行分析，最終得到較原結構更為合理的設計方案，墊板體積減小約10%，同時滿足剛度要求.拓撲優化結合自由形狀優化的方法比以往的“經驗設計”降低人工工作量，在扣件零件的輕量化設計中具有理論意義和實際應用價值.

參考文獻：

[1]

于春華. 城市軌道交通軌道扣件綜述[J]. 鐵道工程學報， 2003， 20（3）： 31-33. DOI： 10.3969/j.issn.1006-2106.2003.03.009.

YU C H. Track fastener of urban rail transit[J]. Journal of Railway Engineering Society， 2003， 20（3）： 31-33. DOI： 10.3969/j.issn.1006-2106.2003.03.009.

[2] 洪清泉， 趙康， 張攀. OptiStruct&HyperStudy理論基礎與工程應用[M]. 北京： 機械工業出版社， 2013.

[3] 周云平， 許健， 劉承科. 摩托車座墊底板剛度有限元分析[C]// 2007年MSC Software中國用戶論文集. 北京， 2007.

[4] 李民， 舒歌群， 衛海橋. 基于拓撲優化和形狀優化的低噪聲齒輪室罩蓋設計[J]. 內燃機工程， 2008， 29（6）： 55-59. DOI： 10.3969/j.issn.1000-0925.2008.06.013.

LI M， SHU G Q， WEI H Q. Design of a low noise engine gear cover based on topology and shape optimization[J]. Chinese Internal Combustion Engine Engineering， 2008， 29（6）： 55-59. DOI： 10.3969/j.issn.1000-0925.2008.06.013.

[5] 郭中澤， 張衛紅， 陳裕澤. 結構拓撲優化設計綜述[J]. 機械設計， 2007， 24（8）： 1-6. DOI： 10.3969/j.issn.1001-2354.2007.08.001.

GUO Z Z， ZHANG W H ， CHEN Y Z. An overview on the topological optimization design of structures[J]. Journal of Machine Design， 2007， 24（8）： 1-6. DOI： 10.3969/j.issn.1001-2354.2007.08.001.

[6] 朱燈林， 陳俊偉， 俞潔， 等. 結構拓撲優化設計的研究現狀及其應用[J]. 機械制造與自動化， 2005， 34（6）： 7-11. DOI： 10.3969/j.issn.1671-5276.2005.06.003.

ZHU D L， CHEN J W， YU J， et al. Developments of structural topology design and it's application in structural design[J]. Machine Building & Automation， 2005， 34（ 6） ： 7-11. DOI： 10.3969/j.issn.1671-5276.2005.06.003.

[7] 曾晶晶， 卜繼玲， 劉建勛. 轉向架齒輪箱吊桿的優化設計[J]. 計算機輔助工程， 2013， 22（2）： 27-30. DOI： 10.3969/j.issn.1006-0871.2013.02.006.

ZENG J J， BU J L， LIU J X. Optimization design of bogie gear box suspender[J]. Computer Aided Engineering， 2013， 22（2）： 27-30. DOI： 10.3969/j.issn.1006-0871.2013.02.006.