包絡線在經濟學中的應用
哈爾濱商業大學基礎科學學院 曲國坤
包絡線在經濟學中的應用
哈爾濱商業大學基礎科學學院 曲國坤
在我們的日常生活中,包絡線的應用非常廣泛,利用包絡線不僅可以解決相關的數學函數問題,而且可以處理很多現實生活中所遇見的經濟問題。本文介紹了包絡線在數學領域和經濟學領域中的運用,其中重點介紹了如何利用包絡線來求函數的最值、包絡線在常微分中的運用、包絡原理,以及包絡線在西方經濟學長期、短期成本曲線中的運用。
包絡線 成本曲線
包絡曲線是西方經濟學中的一個基本概念, 也是分析長期成本中重要的分析工具之一。
1 包絡線的基本概念
1.1 包絡線的幾何學定義常微分方程中對包絡線的定義:設給定一個單參數曲線族為參數。如果存在連續可微的曲線,其上任意一點均有中某一曲線與相切,且對上不同的點,有中不同曲線與之相切,那么稱曲線為曲線族的包絡線。
1.2 包絡線的經濟學定義
在經濟學中,就是各種需求曲線或供給曲線或其他曲線的頂點(所謂的峰點)連接起來形成的一條平滑曲線,就是“包絡線”,看起來就像把許多拋物線“包”起來一樣。
2 包絡線在經濟學中的應用
2.1 包絡定理(1)無約束模型設最大值函數為:


(2)等式約束模型
設最大值函數為:
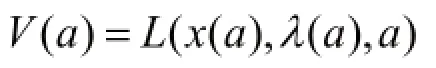
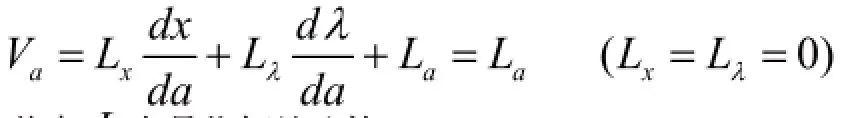
2.2 對包絡定理的說明
例:求

解:方法一:建立拉格朗日函數:

一階必要條件為:


由此可得:
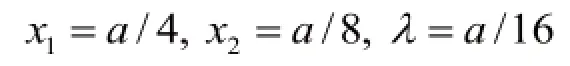
方法三:用傳統方法驗證。

2.3 包絡原理的應用
應用一:證明Shephard's 引理[1]
Xi是生產廠商對相應要素i的派生需,其中成本函數在點是可微的, 則有:
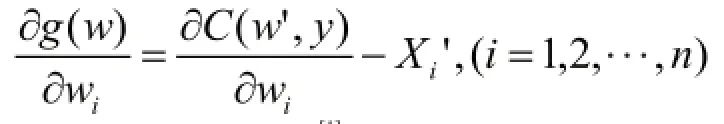
應用二:稅金問題[1]
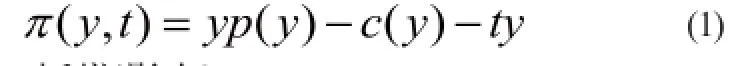
問稅金的變化對利潤影響?

應用三:拉格朗日乘子
(1)約束型參數
有一類特殊的參數是所謂“約束型參數”。例如,消費者的預算線為均為向量)。這里,收入即為約束型參數。
(2)約束型參數對最大值函數的影響
約束型參數對最大值函數的影響有一個非常簡單的結果,即它等于拉格朗日乘子在最優處取值)。
設等式約束模型為:
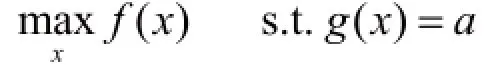
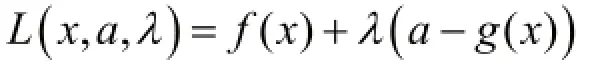
根據包絡定理有:
例如:效用最大化問題
該問題的拉格朗日函數
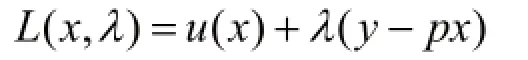
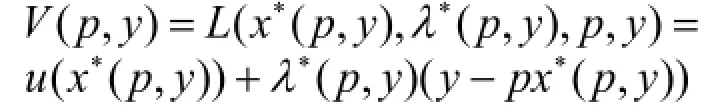
應用四:包絡線指標[2]
兩條移動平均線組成了包絡線技術指標,具體見圖1。市場的變化率決定了相關聯數量的通道邊幅的移動,市場變化率相對較高時,通道邊幅的變化也會表現得相對激烈,市場變化率相對較低時,通道邊幅的變化也會表現得相對弱化。
包絡線指數是由價格變化范圍的上下界來定義的。當價格上升到通道頂端時,出現了賣出信號;當價格下降到通道底端時,出現了購買信號。
包絡線指標實際上就是賣家以及買家共同作用,推動價格達到邊界位置。價格在以上幾點的作用下,不斷移動以至于到達一個相對現實的水平上,最終達到比較穩定的位置。包絡線指標在這一點上保力加通道指標的解釋有共通之處。
圖1 包絡線技術指標
包絡線可以用作預測市場價格在平均價格附近的波動范圍,包絡線的中軸是一條可以移動的平均線,包絡線的上軌以及下軌,用當前均線值加上(減去)固定的百分比。
應用五:分析長期成本
我們可以將長期曲線看作由多個不同短期曲線來構成的,每條不同產量的短期平均成本曲線都可以找到最低點,將所有的最低點連接起來,長期平均成本曲線就是由所有的點構成的。從包絡的角度來講,LTC是STC的包絡線,另外LAC也稱為SAC的包絡線。事實上,長期總成本曲線上的每一個點,它都是表示一個最優的生產規模, 也就是表示相應不同產量下短期成本的最低點,所以,在一個長期的分析過程中,長期平均成本也就對應了廠商按照不同的產量生產,所需要的最低平均成本。按照以上分析的方法,就可以得到長期平均成本的曲線圖。
對于短期平均成本曲線以及長期平均成本曲線來講,每條短期平均成本曲線上都會有一個切點,而對于長期平均成本曲線來講,在它的最低點處,一定會存在一條短期平均成本曲線,此曲線與長期平均成本曲線相切。廠商就可以按照這樣的方式來確定自己的生產計劃,所以長期平均成本曲線又被稱為計劃曲線。
長期平均成本曲線和短期平均成本曲線的區別是:長期成本曲線下降和上升時都相對比較平坦。由此可以看出,長期平均成本在增加和減少的速度上來講,都是相對比較緩慢的,這主要是因為在一個長期的生產過程中,所涉及到的生產要素都要求隨時可以調整,在規模收益遞增和規模收益遞減中間還存在一個階段,即規模收益不變階段;而在一個短期過程中,這個規模收益不變階段是非常短的,或者是不存在的。上述原因導致長期平均成本曲線是短期平均成本曲線的包絡線,而不是各短期平均成本曲線最低點的連線。
把生產規模按極限思想無限細分,將每一條SAC曲線的最低平均成本點,這些最低點就是長期分析中各產量水平所對應的最低平均成本,將所有的點連接起來,構成長期平均成本曲線,如圖2所示。

圖2 構成長期平均成本曲線
另一方面,長期平均成本曲線也可以是短期平均成本曲線的包絡線,但是需要滿足以下幾個條件。首先,要求所有短期平均成本曲線都處于同一個水平線;其次,要求工廠的規模可以無限細分,即可以任意調整,并且要保證在每一個規模的特定產量下,都只有一個最低成本點;再次,生產規模要求服從經濟的遞增、不變和遞減這三個階段規律。
[1] 鄧軍,吳漢洪.西方微觀經濟學中的包絡定理述評[J].北京機械工業學院學報,1994(01).
[2] 崔慧永.談包絡曲線在實踐運用中的矛盾[J].吉林師范大學學報(人文社會科學版),2006(04).
F224
A
2096-0298(2016)08(a)-171-02

