n維單形的體積比

英起志

（江蘇商貿職業學院，江蘇 南通 226011）

n維單形的體積比

英起志

（江蘇商貿職業學院，江蘇 南通 226011）

給出了單形體積比的計算公式，得出了其漸進性質，計算了部分單形的體積比。

n維；單形；John橢球；體積比

單形是凸體幾何中最基本和最重要的凸體之一，n維空間中的單形是n+1個仿射無關點的凸包，它是2維歐式空間的三角形、3維歐式空間的四面體向任意維空間的推廣。n維空間中，由向量v0，v1，…，vn確定的n維單形的體積為：

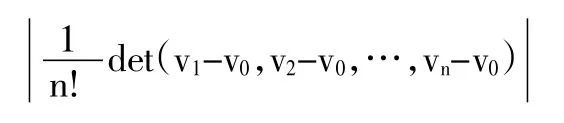
凸體的體積比是凸體的重要特征之一，Rn中凸體K的體積比vr（K）定義為：

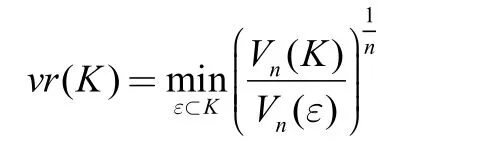
其中ε是包含于K的橢球，Vn（K）和vn（ε）分別表示K和ε的體積。

1948年，Fritz John證明了對于Rn中的任意凸體都包含體積最大的橢球[1]，這就是著名的John橢球定理，其中的橢球被稱為John橢球或L?wner-John橢球。John橢球定理解決了凸體內最大體積橢球的存在性問題，定理的結論和方法被廣泛運用，成為凸體幾何中一系列重要研究的基石。1997年，R Howard在文獻[2]中證明了凸體的John橢球是唯一的，解決了John橢球的唯一性問題。如果一個凸體的John橢球是歐氏單位球，則稱該凸體處于“John位置”，任何凸體都可以在仿射變換的作用下使之處于John位置。R Howard在文獻[2]中還證明了對于任意凸體K，存在橢球E（John橢球），使得：

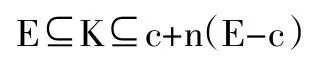
體積比就是在John橢球的基礎上定義的，它對于解決逆等周不等式問題起到了重要作用。Rn中凸體K的體積比定義為：

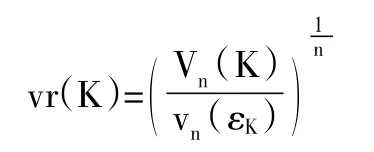
其中εK為凸體K的John橢球.由定義可知，n維橢球的體積比最小，為1，其余凸體的體積比均大于1。凸體體積比的重要性質是仿射不變性。

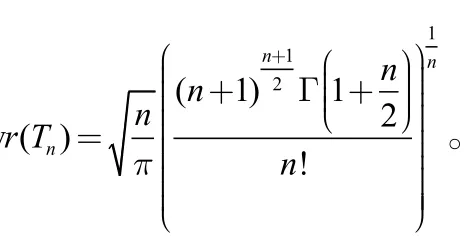
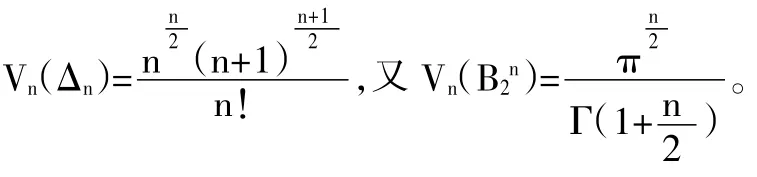
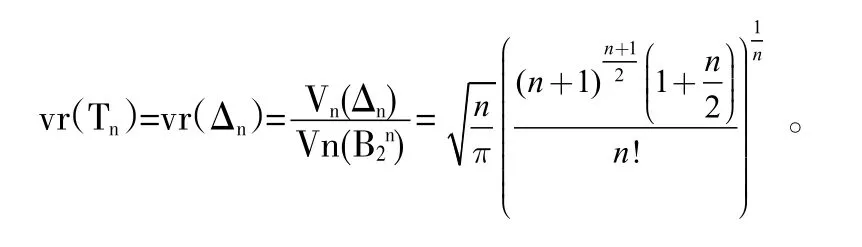
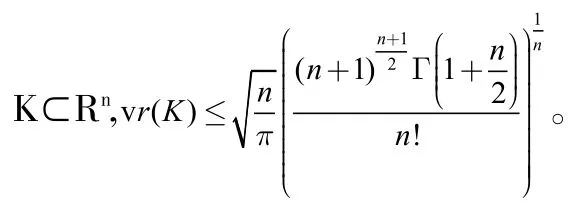
下證當n增加時，vr（Tn）嚴格單調遞增，即對任意正整數n，vr（Tn+1）＞vr（Tn）。

一個正值函數f（x）如果在區間I上滿足

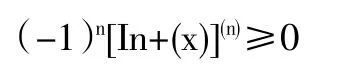
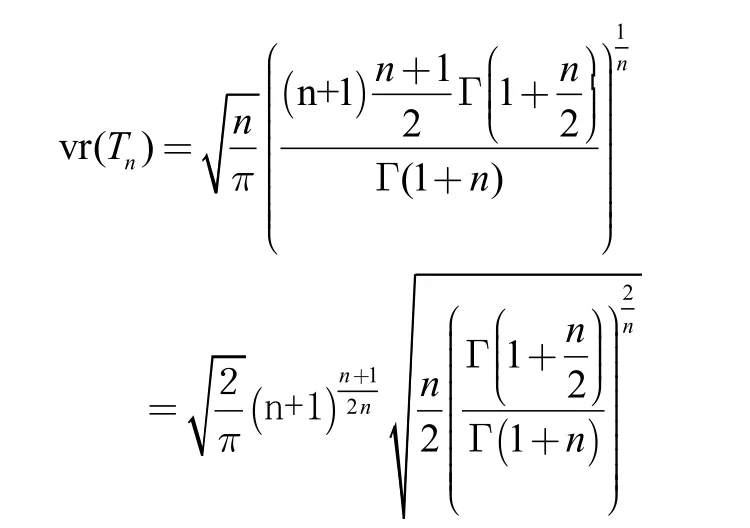
當x＞0時，(lnh(x))'＞0，h(x)＞0，因此h'(x)=h(x)(lnh(x))'＞0，則函數h（x）在（0，+∞）上單調遞增，從而關于n嚴格單調遞增。

綜合以上結論，可知vr（Tn）關于n嚴格單調遞增。

部分n維正方體的體積比的值見表1。

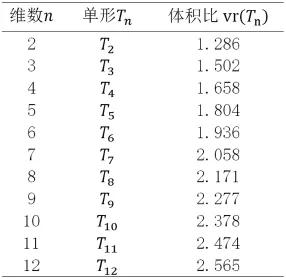
表1 部分單形的體積比（保留3位小數）

[1]John F.Extremum problems with inequalities assubsidiary conditions[M].Courant Anniversary Volume.New York:Interscience,1948：187-204.

[2]R Howard.The John ellipsoid theorem[D].University of South Carolina,1997.

[3]Keith Ball.Volume ratios and a reverse isoperimetric inequality[J].Journal of the London Mathematical Society,1991, 4：351-359.

[4]張素玲,陳超平，等.關于伽瑪函數的單調性質（英文）[J].大學數學，2006（4）：50-55.

[5]Keith Ball.Volumes of sections of cubes and related problem[J].Geometric AspectsofFunctionalAnalysis,1989,1376：251-260.

[6]Keith Ball.Ellipsoids of maximal volume in convex bodies [J].Geometriae Dedicata,1992，41（2）：241-250.

A calculation formula of simplex volume ratio was given,so that we can calculate its asymptotic property and some values of volume ratios.

dimension;simplex;John ellipsoid;volume ratio

O186.5

A

2096-000X（2016）23-0263-02

英起志（1983-），男，江蘇連云港人，江蘇商貿職業學院，數學教研室主任，講師，碩士，研究方向為高職數學教學。