圖像的分形幾何維數(shù)和系數(shù)模擬

圖像的分形幾何維數(shù)和系數(shù)模擬

幾何學(xué)是研究物體組成結(jié)構(gòu)及形態(tài)關(guān)系的一門(mén)學(xué)科。歐幾里德幾何學(xué)的基本構(gòu)圖元素是點(diǎn)、線、面，幾何物體由點(diǎn)、線、面的組合而成，幾何物體元素間的數(shù)量關(guān)系可通過(guò)解析幾何進(jìn)行公式化表述。但如果我們仔細(xì)審視我們生活的這個(gè)星球，甚至將目光放得再遠(yuǎn)一些直至整個(gè)宇宙，我們不難發(fā)現(xiàn)歐幾里德幾何學(xué)表述能力存在許多不足，對(duì)于在自然界中廣泛存在的山脈、河流、宇宙星系等客觀物體，由于它們的具有復(fù)雜的內(nèi)部結(jié)構(gòu)，歐幾里德幾何學(xué)在描述這些不規(guī)則形狀物體及其內(nèi)部細(xì)節(jié)方面存在很多不足。另外，隨著幾何學(xué)研究的不斷發(fā)展，人們研究了康托集合、柯可曲線、斯?fàn)栙e斯基三角形等幾何形狀，發(fā)現(xiàn)歐幾里得幾何遇到了前所未有的挑戰(zhàn)，歐幾里得幾何因無(wú)法準(zhǔn)確描述這些幾何結(jié)構(gòu)而只能給它們標(biāo)上“病態(tài)”標(biāo)簽從而排除在研究范圍之外。1975，Mandebrot質(zhì)疑歐幾里得幾何學(xué)的維數(shù)概念，他針對(duì)英國(guó)的海岸線問(wèn)題進(jìn)行了深入研究，他發(fā)現(xiàn)：測(cè)量得到的海岸線長(zhǎng)度依賴(lài)尺子的尺度，歐幾里德幾何的長(zhǎng)度概念在處理海岸線問(wèn)題時(shí)遇到了困難，為了克服理論上的困難， Mandebrot提出用自相似維數(shù)概念，并用“Fractal”（分形）一詞來(lái)描述海岸線等不規(guī)則幾何形狀，經(jīng)過(guò)不斷的深入研究，分形幾何理論逐漸形成了獨(dú)立的學(xué)科體系，體系內(nèi)容不斷得到豐富和完善，。

分形實(shí)例

康托集合

設(shè)實(shí)數(shù)區(qū)間[0，1] 為E0，令同樣方法去掉E1兩個(gè)子集中間三的三分之一部分，如此循環(huán)往復(fù)，逐步得到Ek，Ek是由2k個(gè)長(zhǎng)度各為3k的區(qū)間組成，令F＝則稱(chēng)F為三分Cantor集。如圖1所示。

圖1 康托集合

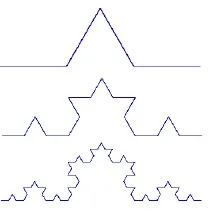
圖2 柯克曲線

柯克曲線

設(shè)E0是長(zhǎng)度為1的線段，按照和三分康托集一樣的方法去掉中間三分之一，在空白處用等邊三角形的另兩邊補(bǔ)充得到E1，按照同樣的規(guī)則對(duì)E1進(jìn)行操作，設(shè)k為操作次數(shù)，當(dāng)

k→∞時(shí)得到的極限曲線F，F(xiàn)稱(chēng)為柯克曲線，如圖2所示。

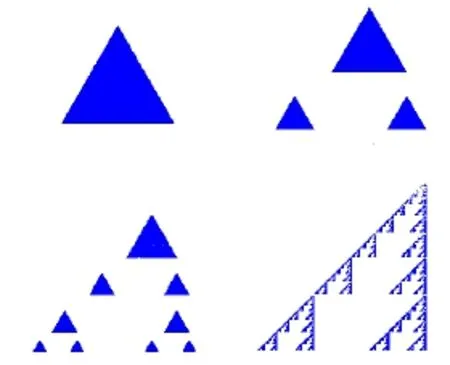
圖3 斯?fàn)栙e斯基三角形

斯?fàn)栙e斯基三角形

任意三角形，取三邊的中點(diǎn)，并將中點(diǎn)連接起來(lái)，將中點(diǎn)圍成的三角形挖掉，得到三個(gè)的三角形，采用同樣的方式挖掉三個(gè)三角形的中心部分，得到九個(gè)三角形，以此類(lèi)推下去，就會(huì)得到如圖3所示的圖形，該圖形成為斯?fàn)栙e斯基三角形。

從傳統(tǒng)歐幾里德幾何角度分析，康托集合和柯克曲線的長(zhǎng)度為零，斯?fàn)栙e斯基三角形的面積也為零，這些圖形顯然與歐幾里德幾何的結(jié)論矛盾，因?yàn)橐痪S物體長(zhǎng)度不可能為零，二維結(jié)構(gòu)的面積也不肯能為零，因此按照歐幾里德幾何的邏輯上述圖形都是“病態(tài)”的。仔細(xì)分析康托集合、柯克曲線、斯?fàn)栙e斯基三角形不難發(fā)現(xiàn)，它們的共同特征是具有精細(xì)結(jié)構(gòu)，即由任意小的細(xì)節(jié)構(gòu)成；整體與局部具有自相似性。

自相似性和自相似維數(shù)

如果物體的整體縮小后能夠與局部重合，我們稱(chēng)這樣的物體為分形物體，物體的這種特征稱(chēng)之為自相似，定義自相似維數(shù)為：

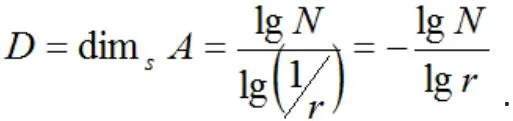
上式中D稱(chēng)為自相似維數(shù)，N為物體的細(xì)節(jié)個(gè)數(shù)，r為相似比。利用上式進(jìn)行計(jì)算，得到康托集合的自相似維數(shù)是，柯克曲線的自相似維數(shù)是，斯?fàn)栙e斯基三角形的自相似維數(shù)是，很明顯，物體的自相似維數(shù)一定是整數(shù)。

康托集合、柯克曲線和斯?fàn)栙e斯基三角形在歐幾里德幾何理論框架內(nèi)都屬于病態(tài)圖形，但在分形幾何理論體系內(nèi)，它們具備了豐富的數(shù)學(xué)內(nèi)涵，即具有嚴(yán)格的自相似特征，并且它們的自相似維數(shù)都是小數(shù)。另外需要指出的是自相似維數(shù)和傳統(tǒng)的歐幾里德幾何維數(shù)是相容的，即傳統(tǒng)幾何物體的自相似維數(shù)和歐幾里德維數(shù)相等。因此自相似維數(shù)的引入豐富了傳統(tǒng)維數(shù)概念的內(nèi)涵。

圖4 斯?fàn)栙e斯基三角形計(jì)算結(jié)果

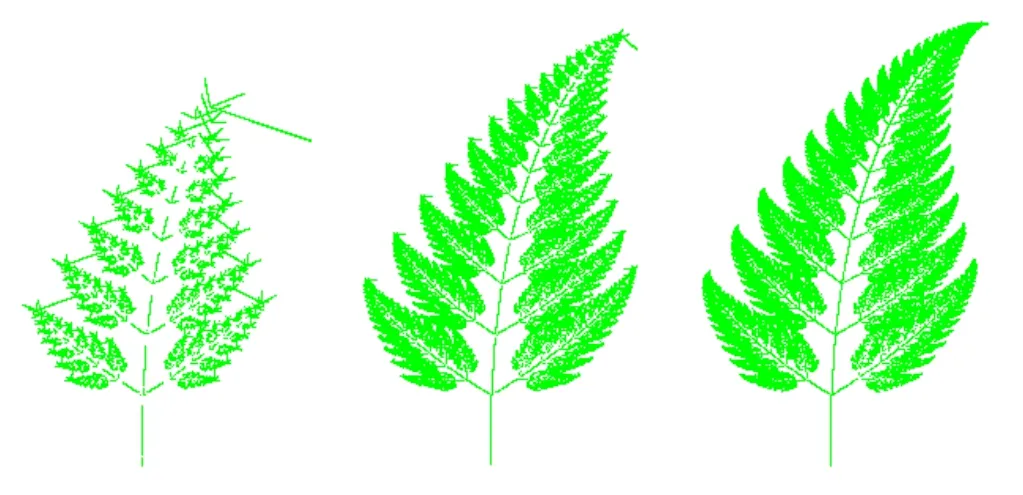
圖5 橛子樹(shù)模擬結(jié)果

分形圖像的構(gòu)造算法

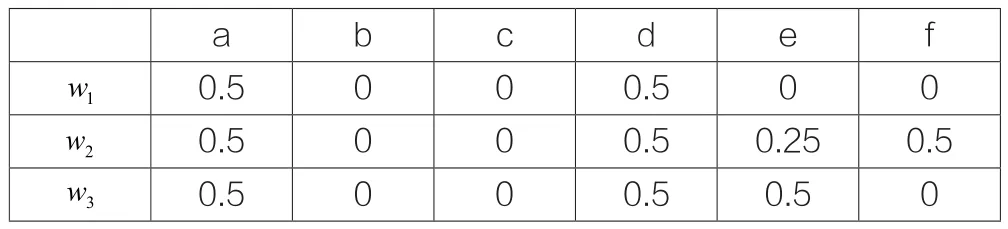
表1 斯?fàn)栙e斯基三角形的變換系數(shù)表

康托集合、柯可曲線也可通過(guò)相同的方法計(jì)算得到。不僅幾何結(jié)構(gòu)可以采用上述算法計(jì)算得到，自然物體同樣也可以用相同的算法進(jìn)行模擬，表2是橛子樹(shù)的構(gòu)造算法系數(shù)表，圖5為計(jì)算模擬結(jié)果。

表2 橛子樹(shù)的變換系數(shù)表

計(jì)算結(jié)果表明：具備自相似特征的分形物體可以采用幾個(gè)仿射變換的方法進(jìn)行構(gòu)造，該構(gòu)造的核心問(wèn)題是選取合適的仿射變換系數(shù)。自然物體雖不具備嚴(yán)格的自相似特征，但它們普遍具有統(tǒng)計(jì)自相似性或局部自相似性，仍然可以通過(guò)仿射變換進(jìn)行構(gòu)造。因?yàn)樽儞Q系數(shù)的數(shù)據(jù)量遠(yuǎn)小于實(shí)際圖像的數(shù)據(jù)量，從而可以實(shí)現(xiàn)數(shù)據(jù)壓縮的目的。有些情況下我們需要實(shí)現(xiàn)圖像目標(biāo)的自動(dòng)識(shí)別，而變換系數(shù)描述了圖像細(xì)節(jié)，因此可以通過(guò)對(duì)比變換系數(shù)的方法實(shí)現(xiàn)計(jì)算機(jī)目標(biāo)自動(dòng)識(shí)別。

10.3969/j.issn.1001- 8972.2016.20.025