《等邊三角形》教學設計

郭 晶

（北京市和平街第一中學朝來校區 北京 100012）

《等邊三角形》教學設計

郭 晶

（北京市和平街第一中學朝來校區 北京 100012）

一、教學目標：

1．了解等邊三角形的概念；探索并初步掌握等邊三角形的性質、判定方法，能夠運用性質和判定解決相關問題．

2．通過探究活動，激發學生的學習興趣，滲透類比、分類、轉化思想，學會用數學思想和方法研究數學問題

二、教學重點難點

重點：等邊三角形的性質及判定．

難點：探索等邊三角形的性質及判定的過程．

三、教學方法：

啟發探究

四、教學過程：

1．創設情境，導入課題

問題1：① 什么是等腰三角形；② 什么是等邊三角形？③ 等邊三角形和等腰三角形有何關系？

設計意圖: 從學生的已有知識出發研究等邊三角形，為本節課打下基礎

2．自主探究、總結性質

活動1：探究等邊三角形的性質

問題1：把等腰三角形的性質用于等邊三角形，能得出什么結論？從哪幾個角度分析性質？

師生行為：引導學生歸納等邊三角形的性質：

（1）等邊三角形的三個角都相等，并且每一個角都等于60°

（2）三線合一

（3）等邊三角形是軸對稱圖形，有三條對稱軸

設計意圖：教師引導學生發現等邊三角形的性質，讓學生經歷從一般到特殊的思維方法

活動2：探究等邊三角形的判定

問題2：類比等腰三角形的判定方法，猜想等邊三角形的判定方法？并證明猜想的正確性。

師生行為：引導學生猜想等邊三角形的判定定理：三個角都相等的三角形是等邊三角形

設計意圖：滲透類比的思想由等腰三角形的判定定理猜想等邊三角形的判定方法。

活動3：類比等腰三角形的判定方法，猜想等邊三角形的判定方法？并證明猜想的正確性。

思考：以下三種畫法能保證得到的△ABC是等邊三角形嗎？并給出證明。

師生行為：畫法1：畫線段AB，并分別以點A、B為圓心，以A B為半徑畫弧，兩弧相交于點C．

畫法2：畫一個角∠PBC＝60°，取BC＝10cm；再以點C為頂點，畫∠QCB＝60°，PB與QC交于點A．

畫法3：畫一個角∠PBQ＝60°，再以B為圓心，以適當長為半徑畫弧，交PB于點A，交BQ于點C

追問1：由畫法3得出什么結論？

頂角等于60°的等腰三角形是等邊三角形嗎？

追問2：底角等于60°的等腰三角形是等邊三角形嗎？

設計意圖：畫法1和畫法2是等邊三角形定義和等邊三角形判定定理1的應用，畫法3引出等邊三角形判定定理2

活動4：問題：等邊三角形的判定方法都有哪些？

師生行為：小結等邊三角形常用的判定方法：

邊：三邊相等的三角形是等邊三角形

角：三角相等的三角形是等邊三角形

邊角：有一個角等于60°的等腰三角形是等邊三角形。

設計意圖：小結等邊三角形常用的判定方法，形成知識體系

3．解決問題

例1如圖，△ABC是等邊三角形，DE∥BC，分別交AB，AC于點D、E

求證：△ADE是等邊三角形

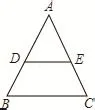
變式1：如圖，△ABC是等邊三角形，在邊AB、AC上分別截取AD、AE，使得AD＝AE．

設計意圖：初步運用等邊三角形的性質和判定。讓學生經歷運用知識解決問題的過程，給學生以獲得成功體驗的空間，激發學習的積極性，變式1用了另一種方法證明等邊三角形

鞏固提高

練習：如右圖，課外活動小組在一次測量測得∠APB=60°，AP=BP=200米，他們便能得到池塘最長處AB為200米，你能說明為什么嗎？

設計意圖：初步運用等邊三角形的性質和判定。讓學生經歷運用知識解決問題的過程，給學生以獲得成功體驗的空間，激發學習的積極性，練習題聯系生活，檢驗等邊三角形判定定理的應用。

4.師生總結，深化新知

以師生共同小結的方式進行。

首先引導學生進行小結：通過這節課的學習你學到了哪些知識？學會了哪些方法？其次，教師鼓勵學生多角度思考問題，并讓學生了解轉化的數學思想。通過師生共同小結，發揮學生的主體作用，有利于學生鞏固所學知識，培養學生的歸納、概括

五、板書設計

§13.3.2等邊三角形

1.定義 3.判定1 例1

2.性質 判定2