試題選擇與高效課堂
——探討復習教學的針對性

☉江蘇省梅村高級中學 劉斌

試題選擇與高效課堂
——探討復習教學的針對性

☉江蘇省梅村高級中學 劉斌

眾所周知，有著十多年數學經驗的教師往往陷入教學的一個瓶頸，即什么都想在課堂教學中講給學生聽、什么都舍不得放棄，結果總是在患得患失中降低了課堂教學的效率.從大量調查顯示，作為教學經驗和精力最為豐富的三十至四十年齡段的教師而言，他們既想全面地提升學生的應試能力，又想學生有一定的數學素養，在教學中常常很多知識舍不得放棄，又沒能找到創新的角度進行整合性教學，往往低效.

我們知道，當下市場上的教輔資料層次不齊，隨手翻閱各種教輔，很多問題雷同，有些問題并不適合各省考綱，學生在題海中耗時耗力，得不償失.而精挑細選的優秀的數學試題卻與眾不同，這些試題凝聚了扎實的數學雙基，又融入了數學思想，用已故特級教師孫維剛先生的話：“我給學生做題，首先自己要做十道題，然后從其中挑選一道題給學生，只有有選擇的才是有針對性的.”筆者認為，在試題泛濫的今天，我們應該選擇有針對性的問題針對性的教學，用研究式的眼光與學生共同分析數學知識和思想方法，讓其真正在課堂復習教學中受益.

一、概念復習的高效性

數學概念是應試考查的重點和難點，而概念復習一直是教師教學的短板.從大量復習課教學現狀來看，筆者發現一些有趣的現象，教師對于知識的復習往往僅限于教輔資料上的試題，換句話說教輔資料給什么問題教師就教什么問題.這種做法顯然是低效和無針對性的.這里筆者例舉兩個不同層次的概念復習是如何設計的，首先舉一個高一新知復習教學的試題選擇設計：

案例1函數奇偶性新知復習設計.

奇偶性是函數的重要性質，對高一新生而言，其對于奇偶性的認知往往僅限于兩個層面，即重要的代數表達式及圖像對稱性.但是學生對這一概念足夠掌握了嗎？概念的理解真正入木三分了嗎？顯然不是的，因為函數模型出現了如分段函數、抽象函數等，學生對于這一概念的理解并不到位.筆者為此選擇了合理的試題層次性，在復習教學中展示了奇偶性復習的高效性.

試題選擇一：①f（x）=2x3+x，x∈R；

②f（x）=2x2+1，x∈［-2.2］；

③f（x）=x2-1，x∈［-2，2）；

④f（x）=x3-x，x∈（0，+∞）.

意圖：首先回顧奇偶性最本質、最初的概念屬性，如何判斷基本初等函數的奇偶性？定義域是首先要考慮的原則，其次是概念的代數屬性運用：f（-x）=-f（x）或f（-x）=f（x），以及幾何屬性入手判斷.

②f（x）=|x-2|+|x+2|；

③f（x）=2|x-2|-|x+2|；

意圖：很明顯，隨著概念初次復習，其頭腦中有了初步判別方式，因此試題選擇從簡單的復合函數入手設計，從新的稍難的函數模型中運用概念，達到函數奇偶性復習的更高境界.

試題選擇三：①f（x）=g（4+x）+g（4-x）（x∈R）；

意圖：試題選擇的第三個層次，是選擇了以抽象函數和分段函數的模型，這里我們知道，學生往往在這兩種模型中使用奇偶性定義的能力是極弱的，歸根到底是定義還不能完全理解.分段函數首先需要驗證定義域的

對稱性，其次考慮其代數屬性f（-x）是否等于f（x）或-f（x）；分段函數，很多學生錯誤率更高的函數模型，歸根到底是無法正確辨別代數屬性中解析式使用的正確性.簡要分析如下：

①它具有對稱性，因為f（-x）=g（4-x）+g（4+x）=f（x），所以f（x）是偶函數，不是奇函數.

綜上可知，在（-∞，0）∪（0，+∞）上g（x）是奇函數.案例2高三函數概念復習設計.

函數概念是中學數學最重要的概念.但是高三函數概念的復習卻并沒有很好的層次性，筆者設計不同層次性的試題來提高復習的高效性.

試題選擇一：（1）M=R，N=R+，法則f：x→x0，是否是函數？

（2）圖1和圖2中的函數滿足（1）中的函數關系嗎？

圖1

圖2

意圖：函數概念的代數屬性考查.

試題選擇二：存在對應法則f滿足，對任意x∈R都有____________.

（1）f（x2+4x）=|x+2|；（2）f（x2-1）=x2+x；（3）f（x2-4x）= x2+4x；（4）f（x2+1）=|x-1|.

意圖：考查函數更本質的含義.很多學生對于函數概念的理解停留在第一層次，即試題選擇一的問題類型，當問題變量呈現復雜狀態，學生就不能清楚地理解自變量所指，以本問題中的第（2）問為例，令x=±1，顯然f（0）= 2或f（0）=0與概念矛盾，其余類似可理解.顯然函數概念的選題和設計立足教材、又明顯高于教材！成為函數概念復習的優秀試題，優化了學生函數概念的本質認知.

二、一題多解的有效性

復習教學離不開解題，更離不開中學數學的優良傳統——一題多解.這是數學教學將知識高效復習的一種優良傳統.選擇怎么樣的試題才會有這種功效呢？筆者認為，一般在課堂復習教學中選擇高考真題效果比較好.高考真題是多位專家歷經多次打磨出的數學好題，其必須具備知識考查的多角度性、解法的多樣性、思維的廣闊性，相比一般的模擬試題，其在知識使用的廣度、運算難度都是拿捏得恰到好處，成為試題選擇和高效課堂的良好切入點.

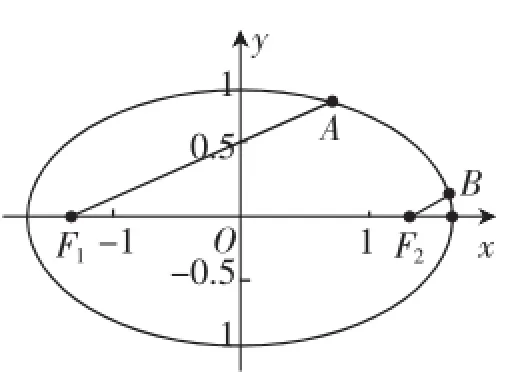
圖3

例題如圖3，設F1，F2分別為橢圓+y2=1的

本題是浙江高考壓軸填空題，也是近年來一道極為精妙的解析幾何小題.以本題作為解析幾何小題的典型，在復習教學中給以呈現，是高效課堂的良好體現.

分析1：我們發現本題條件簡單，題意也是言簡意賅，但是從圖中一分析，學生發現一個最為困難的問題，即F1、A和F2、B四點不共線，教學中常常說的直線和圓錐曲線位置關系中的“設而不求”思想無從下手！因此很多學生是這么入手的：設直線AF1的斜率為k（k＞0），則直線AF1的方程為y=k（x+），聯立橢圓x2+3y2=3，得（1+ 3k2）x2+62x+6k2-3=0.到此處，學生基本停滯不前.筆者認為，學生最直接的思維也是值得教學關注的，因此教師繼續引導學生：結合圖3可知xA=，同理xB=.又因為，所，所以|F1A|=5|F2B|，得，此時xA=0，點A的坐標是（0，1）；同理，當k≤0時，點A的坐標是（0，-1）.很明顯，這樣的方法選擇是不利于思維培養的，過于簡單的問題解決思維帶來了大量的運算.

圖4

分析2：我們要思考，為什么這樣言簡意賅的問題會成為高考壓軸小題呢？如何將分析1中的四點不共線結合到解析

幾何的設而不求思想呢？通過圖形研究，我們發現這里涉及很重要的橢圓性質——對稱性！只需要利用橢圓對稱性將F2B對稱到圖4中F1B1位置，可得|F1A|=5|F1B1|，設而不求的思想躍然紙上！不妨設直線AF1與橢圓的另一個交點為B1，設點A的坐標為（x1，y1），點B1的坐標為（x2，y2），由及橢圓對稱性，可得|F1A|=5|F1B1|，得y1=-5y2.設直線AF1的方程為x=ty-，聯立橢圓+y2=1，得，由韋達定理得y1+y2=因為y1=-5y2，所以，即，得y1=±1.故點A的坐標是（0，±1）.顯然，這應該是問題考查的真正意圖.橢圓對稱性的利用讓問題的解決回歸到學生熟悉的層面，高考真題的選擇讓橢圓幾何性質對稱性的復習入木三分！

總之，試題選擇設計的優良影響著復習教學的效率.筆者從試題選擇和復習教學是否高效有效的角度思考了三個問題：第一，復習教學我們是否真正重視過試題的選擇性？這種選擇是為了更有效的教學，從當下不少無針對性的題海訓練來看，我們合理地選擇試題是否可以成為常態化？第二，好的試題給學生帶來的不僅僅是數學知識運用的綜合性，更是一種美感，如本文中橢圓優美的對稱性，因此我們是否足夠細致地研究了高考真題？第三，教學需要不斷的研究和與時俱進，我們總在用以往的經驗和眼光進行復習教學，是否教師也該思考復習教學如何推陳出新？帶著這樣的問題，懇請讀者繼續批評指正.

1.黃嚴生，束從武.例談“問思”教學法［J］.中學數學教學，2013（1）.

2.周立志.巧用課堂教學中的典型錯誤提升課堂效率的若干策略［J］.中學數學教研，2013（4）.

3.殷偉康.數學課堂教學中追問的特征與時機［J］.數學教學研究，2013（1）.F