學而勤思方可融會貫通
——略談高中數學學習中解題技巧

劉亞林●

山東省濱州市惠民縣第一中學高二·5班(251700)

?

學而勤思方可融會貫通
——略談高中數學學習中解題技巧

劉亞林●

山東省濱州市惠民縣第一中學高二·5班(251700)

本文主要是通過解函數題時，產生思路偏差，從而引發了我們對高中函數解題技巧的研究，其主要方法就是從定量角度進行研究，最終得出了解決高中數學函數分類、數形結合的解題技巧.

思路；錯誤；高中；數學；解題；技巧

一、問題出現

下面選項中，y是x的函數的是( ).

(1)y=x2(x∈N)； (2)y2=x； (3)y=2； (4)x2+y2=1；(5)y=lg(1-x)+lg(x-1)； (6)xy=8； (7)y=sin2x+cos2x； (8)

年份x1949195419591964196919741979198419891994人口數y(百萬)54260367270580790997510351107117

在進行解答時，根據函數的定義變化過程中存在兩個變量，其中一個變量在一定的范圍內變化，另一個變量就有與之相對應的值.因此，在選擇時我選擇了第二項，忽略了第八項.但實際結果是第八項是正確的，第二項是錯誤的.為什么會出現這種問題呢？

二、問題分析

仔細研究解題的過程中，題目所問的是關于y的函數，這就意味著y是因變量，x是自變量.其實函數定義中還有最重要的一點是因變量有唯一確定的值與自變量相對應.這也意味著關于y的函數，x在變化時，y有唯一確定的值.反觀選項(2)y2=x，當x變化時，y并不是唯一確定的值與之相對應.這就是解題錯誤的原因.

三、問題解決及延伸

從上述選項y=x2(x∈N) ，可得出關于y的二次函數是符合函數定義.而(5)y=lg(1-x)+lg(x-1)的定義域是空集，不是函數.(3)(8)是常數函數也是符合函數定義的.但類似(4)對x≠1時，y有兩個值與x對應，不符合函數定義.因此，在遇到類似問題時，可根據函數類型進行判斷，這就是分類解題技巧.

如果將上述選項演化成圖形進行觀察會更加直觀，這種解題技巧屬于數形結合解題技巧.如以下例子：

下列圖形可表示y為x的函數的是____.

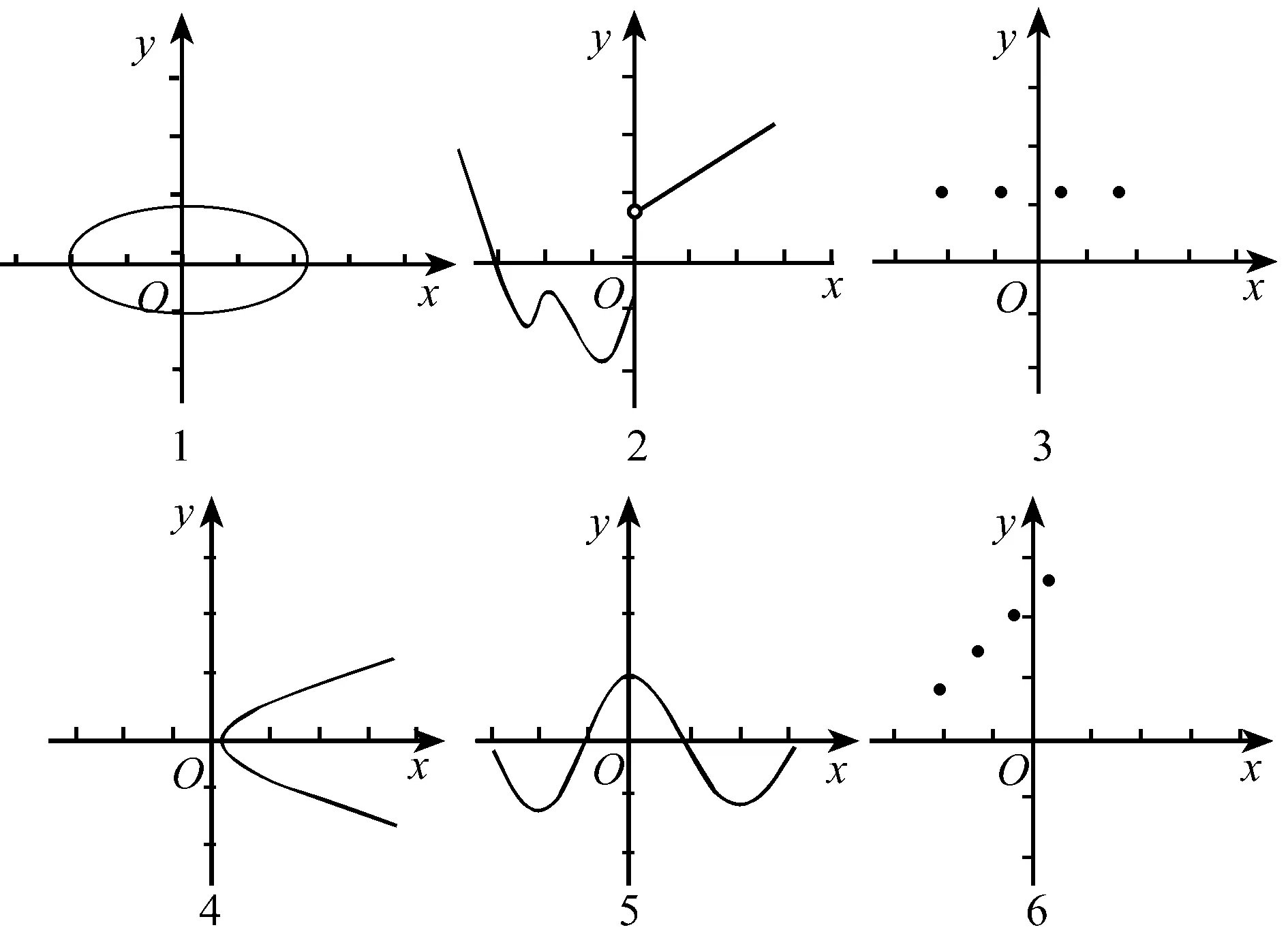
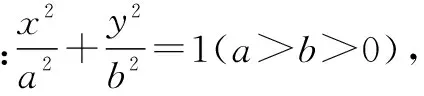
四、應用舉例

例 下列圖中表示y是x的函數的是( ).

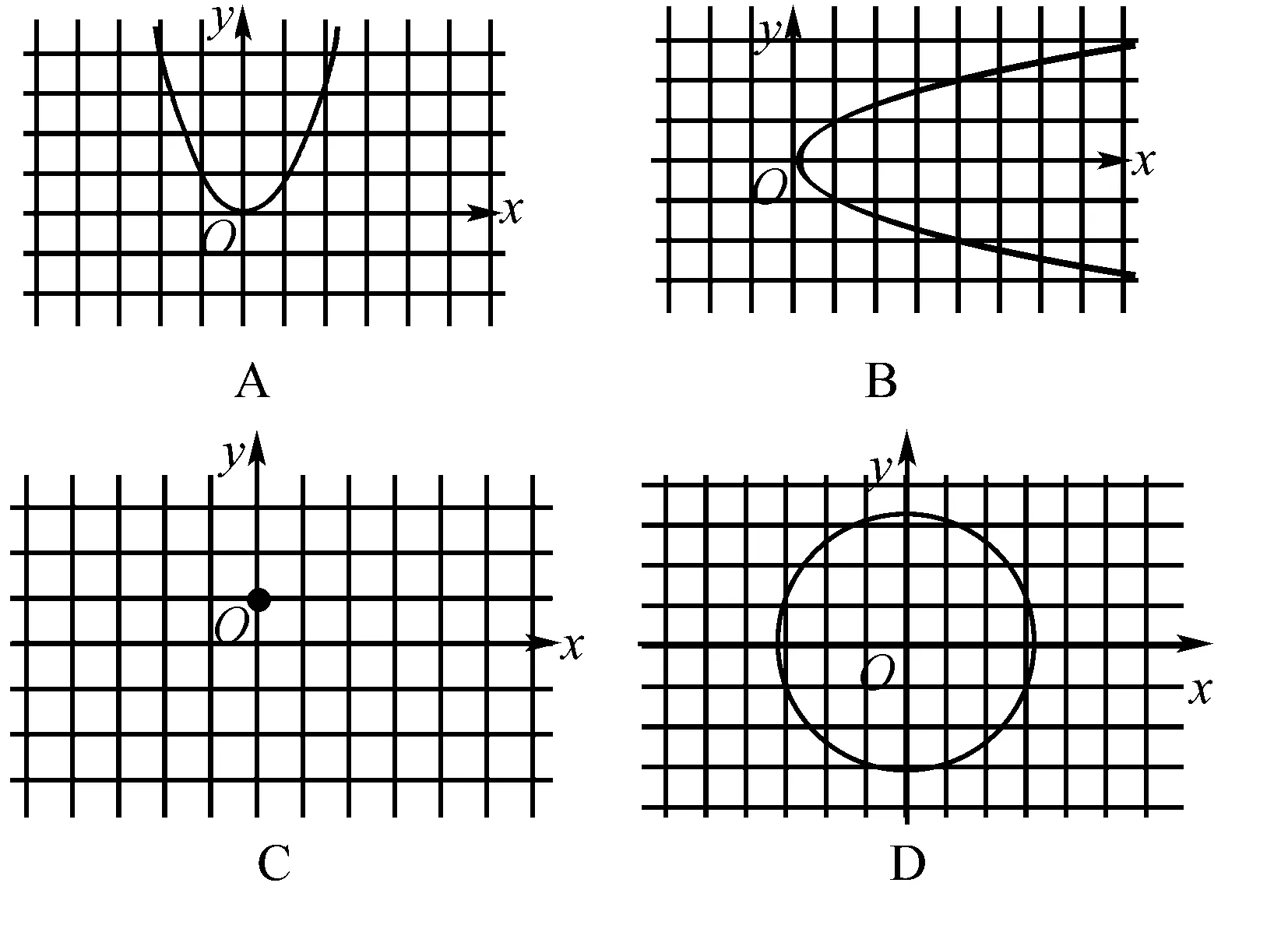
解析 選項A：對于x的每一個值都有唯一的y值與之對應，故y是x的函數.選項B：對于x的每一個大于0值都有兩個y值與之對應，故不可表示y是x的函數.選項C：對于x=0有兩個y值與之對應故不可表示y是x的函數.選項D：對于x的每一個值都有兩個y值與之對應，故不可表示y是x的函數.故A正確.

(指導教師：張士明)

G632

B

1008-0333(2016)28-0027-01