抓住運動規律,巧解動點問題
江蘇省射陽縣實驗初級中學(224300)
李立松●
?
抓住運動規律,巧解動點問題
江蘇省射陽縣實驗初級中學(224300)
李立松●
圖形中的動點問題是近年來中考數學的熱門考點之一,這種題型結合多方面的知識,難度較高.學生們遇到此類問題往往找不到解題的切入口,因此,歸納常見動點問題的常規解法具有重要的意義,這有利于提高學生的思維能力,幫助學生脫離“歧路”,尋找到行之有效的方法.動點問題常與其他章節的知識點結合考察,我將借助相關例題幫助學生理解思路.
一、點的運動產生的規律歸納題
在點的運動過程中尋找規律的題目實際上就是通過觀察點的運動軌跡,從而歸納總結出一條規律,解這種題目要重點把握點在運動初期的規律,從最初的幾個點入手,這樣能使解題過程更加流暢.
例1 如圖1在一個坐標系中,有一個等邊三角形,它的頂點O與坐標原點O相互重合,一條邊OP落在X軸所在的直線上,如果把這個等邊三角形沿著X軸的正方向連續轉動2014次,求最終點P的坐標.
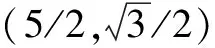
點撥 由最初的狀態往后逐步探索,然后總結出規律,最終運用這個規律進行求解,這是處理這種類型題目的基本方法.
二、點的運動產生的最小長度問題
在點的運動過程中求最小長度,往往結合數形結合的思維方法,要充分利用圖形本身的屬性,如對稱性等性質,如果學生能留心這些特殊的屬性,那么往往能避免復雜的計算,給解題帶來意想不到的幫助.

例2 在如圖2所示的直角坐標系中,正方形AOCB的邊長為12,P點在對角線BO上面運動,D點在邊AO上面,它的坐標為(5,0),連接PD,AP,試求線段PD,AP長度之和的最小值.
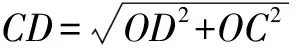
點撥 這道題目根據對稱型把距離之和巧妙地轉化成為求直角三角形的斜邊長,簡化了解題步驟,學生要留意這種巧妙的解法.
三、點的運動產生的函數最值題
點在函數圖像上運動,往往能和其他的點構成不同的圖形,與圖形有關的量有時容易用函數關系表示,有時需要經過轉化才能表示出來,學生要開闊思維,尋找最佳的轉化方法,然后根據求解函數最值的方法便可求解.
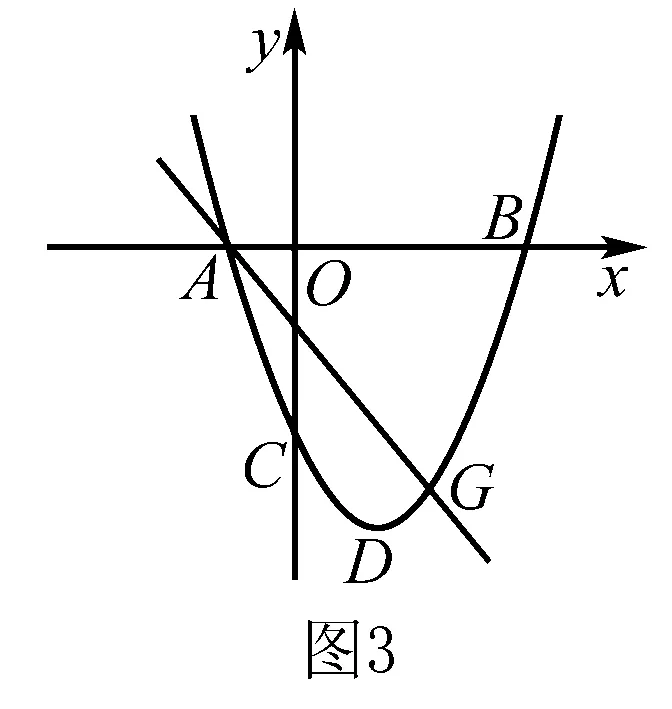
例3 在如圖3所示的坐標系中,二次函數y=x2-2x-3的頂點為D點,它的圖像與y軸相交于C點,與X軸的負方向相交于A點,與X軸的正方向相交于B點,如果點G是其圖像上的一點,它的橫坐標為2,P點在拋物線上并且處于直線GA的下方,試求S△PGA的最大值以及此時P的坐標.
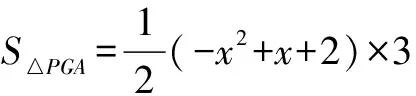
點撥 因為P點處于運動狀態,直接求解AP邊上的高十分困難,這道題中用分割三角形面積的方法避免了求高時的復雜計算,這種方法值得學生借鑒.
以上總結為三類常見的動點問題,正如解題過程所示,三類問題對應著三種基本數學思想分別為:歸納,數形結合以及函數思想,學生在訓練動點問題時應該不斷強化這三種思想,從而有效地提高解題能力.
G
B

