反比例函數研究提升思維水平和解題能力
江蘇省揚州市廣陵區頭橋中學(225109)
孫 靜●
?
反比例函數研究提升思維水平和解題能力
江蘇省揚州市廣陵區頭橋中學(225109)
孫 靜●
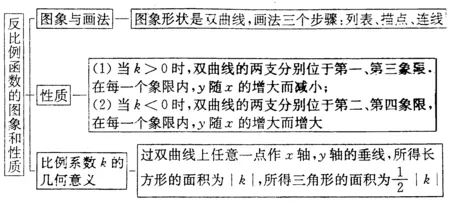
反比例函數一般可表示為y=k/x(k是常數k≠0).反比例函數解析式也可寫成y=kx-1的形式,自變量x的取值范圍是x≠0的一切實數,函數值取值范圍也是x≠0的一切實數反比例函數的圖象是雙曲線,它有兩個分支,這兩個分支分別位于第一第三象限或第二第四象限,它們關于原點對稱,由于自變量x≠0函數值y≠0,因此它的圖象與x軸y軸都沒有交點,即雙曲線的兩個分支無限接近坐標軸,但永遠與坐標軸不相交.本文對反比例的圖象與性質,反比例函數與一次函數的圖象的綜合應用,反比例函數圖象與有關面積問題舉例探討,供讀者參考.
雙曲線;反比例圖象性質;反比例系數K的幾何意義
一、反比例函數的圖象與性質
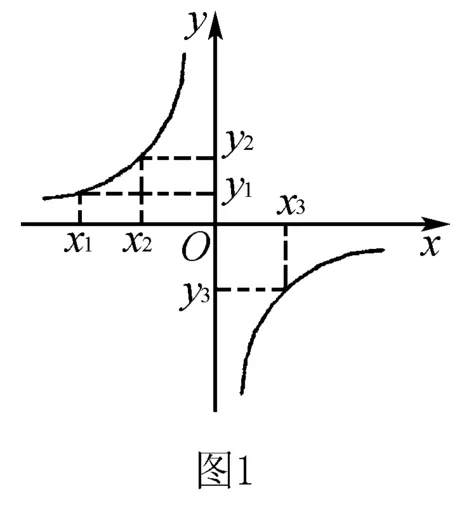
A.y2 C.y1 解析1(性質法) 當k<0時,反比例函數的圖象在第二、第四象限,且在每個象限內,y隨x的增大而增大,此題中需要注意的是(x1,y1),(x2,y2),(x3,y3)不在同一象限內,因為k=-m2-1=-(m2+1)<0,所以函數圖象在第二、第四象限內,所以y2>y1>0.因為x3>0,所以(x3,y3)在第四象限內,所以y3<0,所以y3 比較函數值的大小時,在同一分支上的點可以通過比較其橫坐標的大小來判斷函數值的大小,不在同一分支上的點,依據與x軸的相對位置來進行函數值大小的比較.特殊值法簡單直接,圖象法形象、直觀,是解決此類題目的常用方法. (1)求反比例函數和一次函數的解析式; (2)根據圖象寫出使得反比例函數的值大于一次函數的值的x的取值范圍. 分析 (1)由點N可求出反比例函數的解析式,進而可求出點M的坐標.由N,M兩點可求出一次函數解析式. (2)由y=k/x的圖象與y=ax+b的圖象的交點進行分析,找到y=k/x的圖象在y=ax+b的圖象的上方時對應的x的取值范圍即可. ∵A,B兩點坐標為A(0,2),B(0,-2) ∴AB=4. G632 B 1008-0333(2016)21-0034-01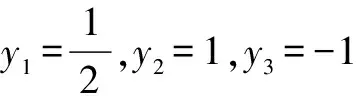
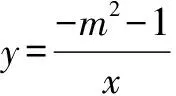
二、反比例函數與一次函數的圖象的綜合應用
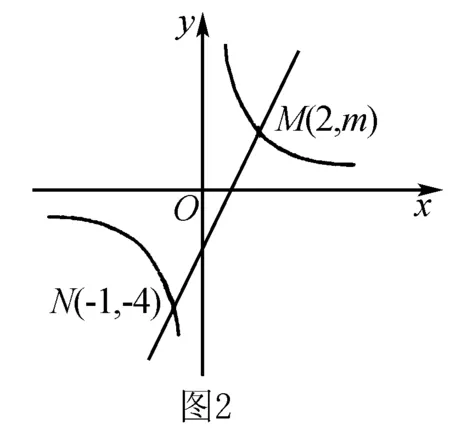
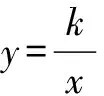
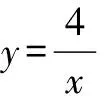
三、反比例函數圖象與有關的面積問題
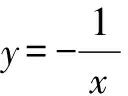
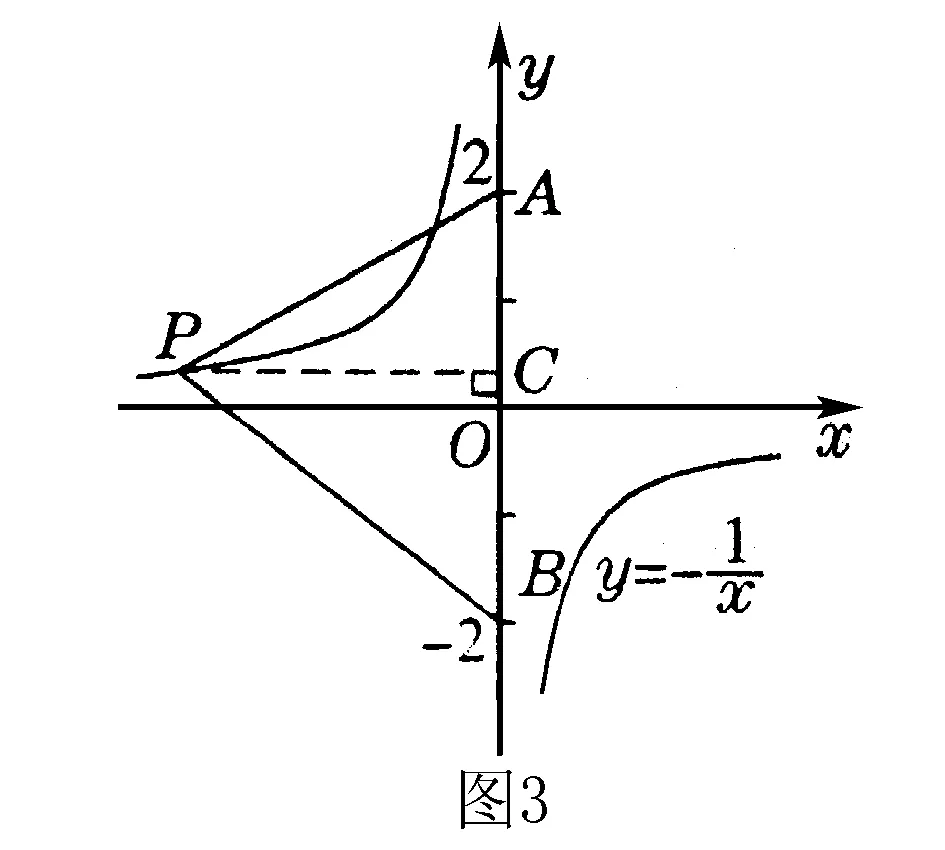
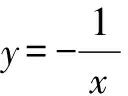
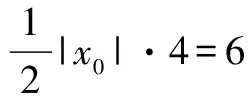
四、重點內容小結