一種面向動態發展系數a的新灰色預測模型
黃輝
(重慶工商大學 電子商務及供應鏈重慶市重點實驗室,重慶 400067)
一種面向動態發展系數a的新灰色預測模型
黃輝
(重慶工商大學 電子商務及供應鏈重慶市重點實驗室,重慶 400067)
既有灰色預測模型發展系數a是在滿足原始序列模擬誤差最小約束下,通過最小二乘法來求解的,當建模系列確定之后,發展系數a即隨之確定,而缺乏與外部系統狀態的同步變化,這是造成現有灰色模型性能不穩定的重要原因。文章通過離散灰色預測模型對發展系數a的動態性進行了研究,并在此基礎上構建了一種發展系數a可動態變化的AGM(1,1)預測模型,最后應用該模型對我國天然氣消費量進行了模擬及預測,且取得了較好的效果,從而進一步驗證了基于動態發展系數a的新模型AGM(1,1)的有效性與實用性。
灰色預測模型;發展系數a;動態性;AGM(1,1)模型;天然氣消費量預測
0 引言
預測是決策的基礎。所謂預測,就是基于既有數據資料,分析系統發展規律或演化特征,并假定系統將按該規律或特征向前發展,在此基礎上實現系統在未來某個時點發展趨勢的預估。科學合理地分析系統發展歷史規律是實現準確預測的基礎,而假定系統將按既有歷史規律發展則是實現有效預測的前提。預測通常只能處理常規性問題,對于非常規性突發事件,預測方法常常“失效”。比如,可以通過最近幾年我國GDP發展趨勢來推測我國在未來某年的GDP增長情況,但是如果期間發生戰爭或者大規模自然災害,則所預測的GDP數據可能誤差很大。預測分為定性預測和定量預測兩類,前者主要通過經驗推測或判斷來實現,帶有較大的主觀性;后者通常數學方法來抽象和描述系統發展規律,并在此基礎上實現預測,這類數學方法通常被稱為定量預測模型。
以GM(1,1)為代表的灰色預測模型是灰色系統理論的核心,是處理“小樣本、貧信息”不確定性預測問題的常用方法[1],主要利用少量有效數據和灰色不確定性數據,通過序列的累加生成,揭示系統未來發展趨勢[2,3]。現有灰色預測模型建模參數都是在滿足原始序列模擬誤差最小約束下,通過最小二乘法來求解的,換言之,當建模系列確定之后,模型參數隨之確定,而且該參數貫穿于模擬與預測的整個過程[4-6]。在灰色理論中,對于相同的灰色預測模型,參數不變則模型不變;因此,現有灰色系統用一個恒定模型去模擬和分析不斷變化著的復雜系統,其模擬可靠性與預測科學性難以得到有效保障,這是導致現有灰色模型模擬及預測精度不穩定的重要因素。本文嘗試對GM(1,1)模型發展系數a的動態性進行研究,通過DGM(1,1)模型動態描述a的變化過程與發展態勢,在此基礎上構建一種發展系數a可動態變化的AGM(1,1)預測模型,最后通過應用該模型對我國天然氣消費量進行了模擬及預測。
1 GM(1,1)模型基本概念
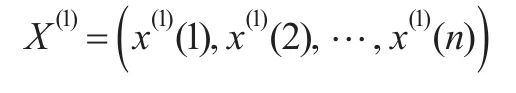
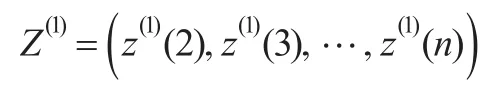
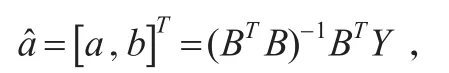
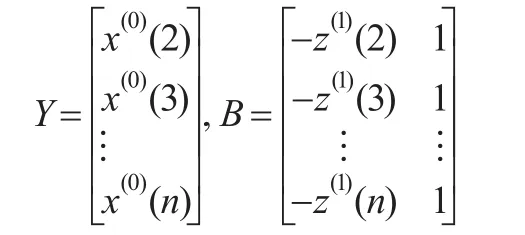
GM(1,1)模型x(0)(k)+az(1)(k)=b的時間響應序列為:
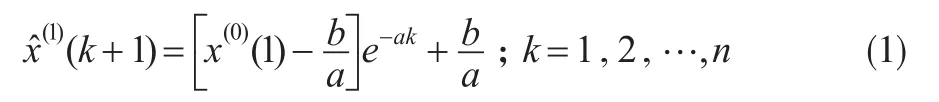
GM(1,1)模型x(0)(k)+az(1)(k)=b的還原值為:
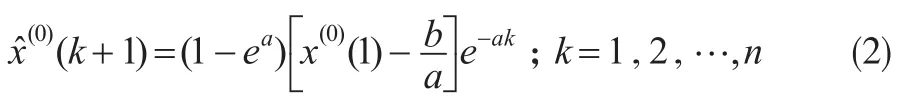
在GM(1,1)模型中,參數-a稱為發展系數,其大小反映了(1)及(0)的發展態勢;參數b稱為灰色作用量,它反映了表征系統行為數據的變化關系,是從背景值挖掘出來的數據,其確切內涵是灰的。GM(1,1)模型的建模流程[1]如圖1所示。
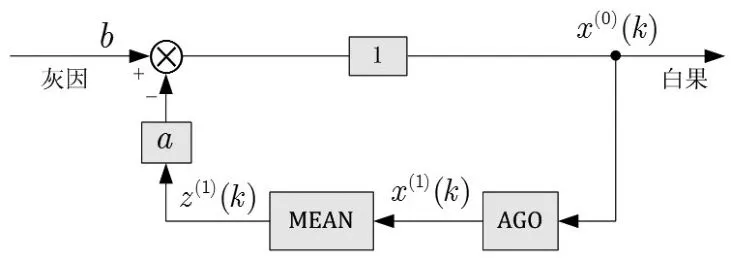
圖1 GM(1,1)建模流程圖
2 發展系數a的動態性及AGM(1,1)模型的構建
當k=2,3,…,n時,設GM(1,1)模型對應的發展系數為a2,a3…an,則根據GM(1,1)模型的基本形式可得:
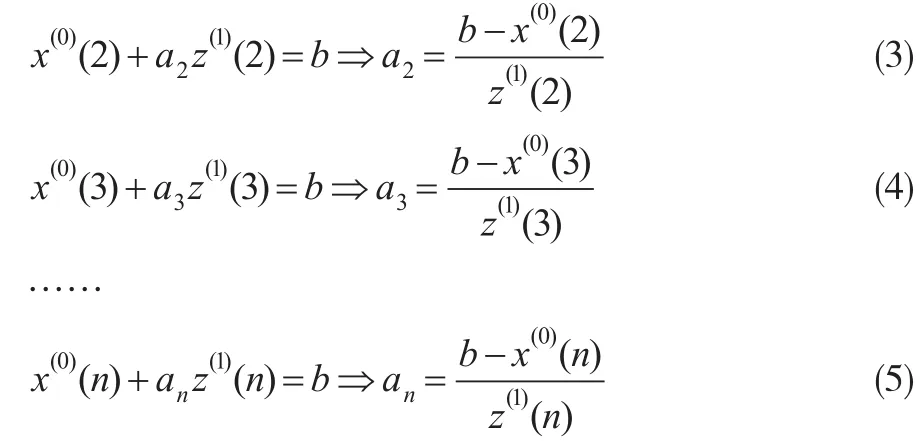
在公式(3)—公式(5)中,參數b為GM(1,1)模型的灰色作用量,x(0)(2),x(0)(3)…x(0)(n)及z(1)(2),z(1)(3)…z(1)(n)為建模數據,均為已知參數,因此可以計算得到GM(1,1)模型對應的發展系數a2,a3…an的值。設GM(1,1)模型對應的發展系數構成的序列為A=(a2,a3…an),構建序列A的離散灰色預測模型(即DGM(1,1)模型),其時間響應序列及還原值分別為:
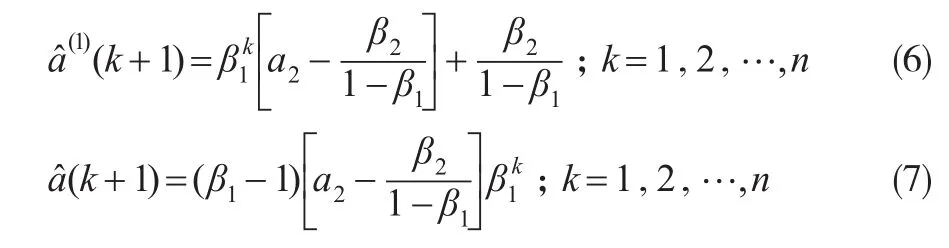
將通過DGM(1,1)模型動態模擬得到的GM(1,1)模型發展系數(k+1)代入公式(2),從而實現GM(1,1)模型發展系數a的動態生成。則變化后的GM(1,1)模型為:
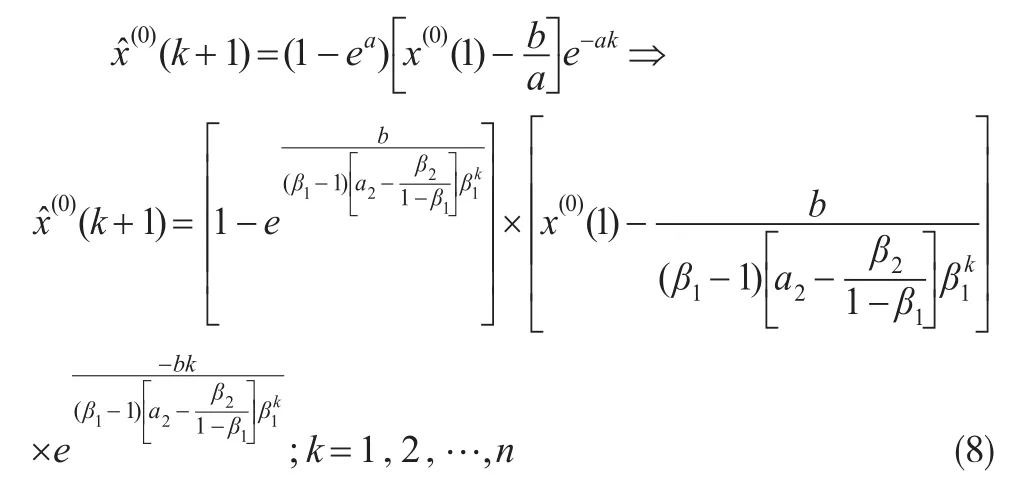
公式(8)稱為發展系數a可調的動態GM(1,1)模型,簡稱AGM(1,1)模型。該模型通過離散灰色模型動態模擬發展系數a的變化趨勢,進而實現了與外部系統的同步變化,理論上具有比靜態發展系數a更高的模擬及預測性能。
3 模型應用與比較分析
本文采用AGM(1,1)模型模擬2006—2013年我國的天然氣需求量,在此基礎上對我國天然氣需求量進行預測。2006—2013年我國天然氣消費量如表1所示。
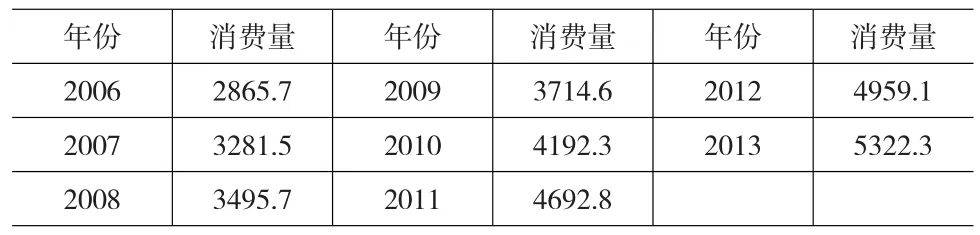
表1 2006—2013年我國天然氣消費量(十億立方米)
(1)參數b及發展系數A的計算
根據GM(1,1)模型參數的計算方法及公式(3)—公式(4),可計算得AGM(1,1)模型的參數b及發展系數A,如下:

(2)DGM(1,1)模型參數β1及β2的計算
根據DGM(1,1)模型的建模機理及灰色系統建模軟件,可計算DGM(1,1)模型參數β1及β2,如下所示:
β1=-0.0156,β2=-0.0782
(3)我國天然氣消費量的模擬值及模擬誤差
將計算得到的參數b及β1、β2代入公式(8),可計算得2007—2014年我國天然氣消費量的模擬值及模擬誤差,如表2所示。
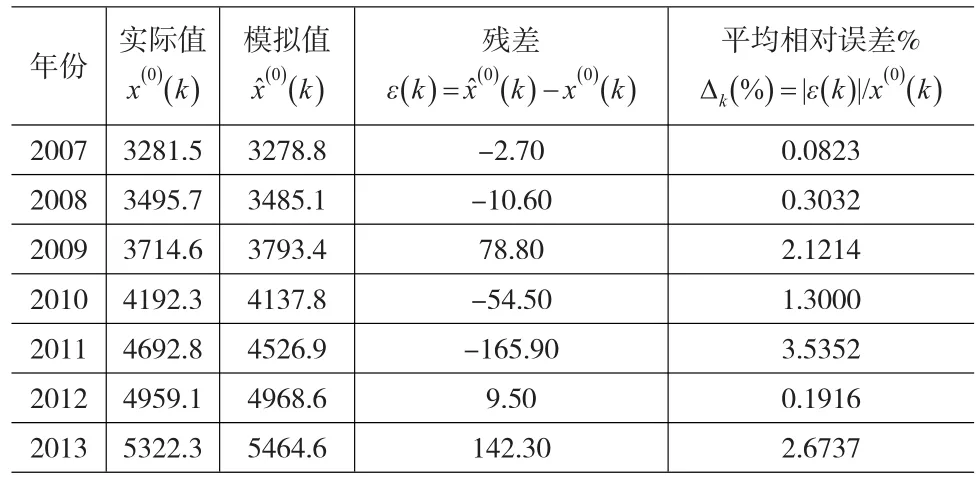
表2 基于AGM(1,1)模型的我國天然氣消費量的模擬值、殘差及平均模擬相對誤差
根據表2可知,應用AGM(1,1)模型模擬2007—2013年我國天然氣消費量的平均模擬相對誤差為:

將表2中的Dk值代入公式(9),可得
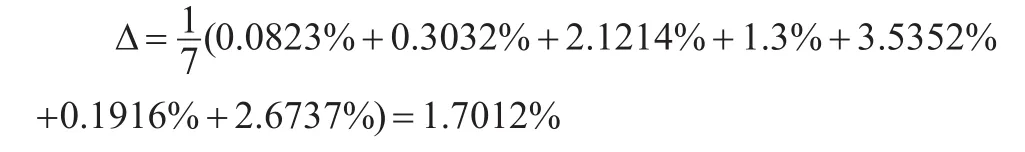
查灰色預測模型精度等級參照表可知,基于AGM(1, 1)模型的我國天然氣消費量的平均模擬相對誤差接近1級,可以用于預測。
(4)我國天然氣消費量的預測
應用AGM(1,1)模型預測2014—2018年我國天然氣消費量,如表3所示。

表3 2014—2018年我國天然氣消費量預測數據(十億立方米)
4 結論
現有的灰色預測模型建模參數都是在滿足原始序列模擬誤差最小約束下,通過最小二乘法來求解的,當建模系列確定之后,模型參數即隨之確定,而且該參數貫穿于模擬與預測的整個過程。可見,現有的灰色建模方法用一個恒定模型去模擬和分析不斷變化著的復雜系統,其模擬可靠性與預測科學性難以得到有效保障,這是導致現有灰色模型模擬及預測精度不穩定的重要因素。本文通過對GM(1,1)模型發展系數a的動態性進行研究,通過數學模型動態描述a的變化過程,在此基礎上構建一種發展系數可動態變化的新灰色預測模型,并通過應用該模型對我國天然氣消費量進行了模擬及預測,從而研究了新模型的模擬和預測性能。
[1]Deng J L.Introduction to Grey System Theory[J].The Journal of Grey System(UK),1989,1(1).
[2]Wu L F,Liu S F,Cui W.Non-Homogenous Discrete Grey Model With Fractional-Order Accumulation[J].Neural Computing&Appli?cations,2014,25(5).
[3]Xie N M,Liu S F.Discrete Grey Forecasting Model and Its Optimiza?tion[J].Applied Mathematical Modeling,2009,33(2).
[4]仇世偉,劉思峰.GM(1,n)模型的離散化結構[J].系統工程與電子技術,2006,28(11).
[5]謝乃明,劉思峰.離散灰色模型的拓展及其最優化解[J].系統工程理論與實踐,2006,(6).
[6]陳繼光.區間灰數DGM(1,1)模型在負荷統計數據預測中的應用[J].統計與決策,2014,(7).
(責任編輯/易永生)
N941.5
A
1002-6487(2016)21-0019-03
國家自然科學基金資助項目(71271226);教育部人文社會科學規劃項目(14YJAZH033);重慶市高等學校教學改革研究項目(1202010)
黃 輝(1965—),男,重慶人,教授,研究方向:管理科學定量方法。

