基于改進Black-Scholes模型的人力資本內在期權價值估計

廖特明，譚志勇

（西南石油大學 經濟管理學院，成都 610500）

基于改進Black-Scholes模型的人力資本內在期權價值估計

廖特明，譚志勇

（西南石油大學 經濟管理學院，成都 610500）

文章結合期望在職時間、人力資本映射資產價值的現金流現值等要素構建了企業人力資本內在價值基礎期權折算模型，并結合疊期循環特性的人力資本內在價值期權化利益實現進行Black-Scholes模型的改進，從而進一步實施具備復合疊套特性的企業人力資本內在價值期權估計中的應用驗證。同時，將基于Black-Scholes模型的企業人力資本期權價值層級的疊套演進行為以層級跳躍為判斷依據進行折算，并利用期權價格的隨機最優控制作為區間問題進行折算。結果證實：改進Black-Scholes模型在針對疊套以及跳躍行為的人力資本變動過程中，為企業的人力資本存留決策提供了較好的驗證及測度價值，但在企業存在更為顯著的人力資源動態調整期間的期權價值預測中，需要結合綜合投入成本進行相應的人力資本期權價值估計。

改進Black-Scholes模型；人力資本；期權價值；估計；應用

0 引言

隨著經濟社會和產業結構調整的進一步發展，人力資本對于經濟增長的影響和推動作用也得以逐步加深。這同時也意味著人力資本對于企業而言存在著越來越重要的價值意義。對于人力資本價值的估計，無論是企業自身還是學術界都開展了深入的分析，對于企業人力資本內在價值的剖析運用了很多豐富的理論和驗證工具。而人力資本自身存在豐富的流動性和一定程度的價值權衡屬性，因此，如何更為客觀地反映人力資本對于企業經營管理乃至市場競爭生存的價值，對于企業戰略實施，一個國家的產業發展都具有重要而深刻的意義。為此，本文從人力資本自身的流動性和人力資本績效表現、屬性變動等角度進行了人力資本內在價值的估計。

現有研究主要是針對以人力資本價值期權預測進行了模型選取，以及模型預測分析精度提升的論證，選用模型主要集中在基礎Black-Scholes模型，同時對于存在疊套以及跳躍的人力資本要素屬性，在其測度上缺乏適應調整，以及進一步的細分。為此，本文結合期望在職時間、人力資本映射資產價值的現金流現值等要素，構建了企業人力資本內在價值基礎期權折算模型，并就人力資本要素期權價值現金流轉換過程中的疊套甚至跳躍進行了參數與轉化過程細分，并將其以層級跳躍為判斷依據加以折算，形成針對企業人力資本內在期權價值的預測。

1 企業人力資本期權價值測度基本模型

根據上述分析可知，人力資本內在價值不同于一般意義上的實物期權、金融期權，從本質而言，企業人力資本期權屬性上存在對應金融期權部分的當前價值，而該類期權在其價值部分可以對應其當前價值，也即是企業人力資源在期權屬性上所產生的預期現金流對應現值。同時，以人力資本內在價值對應的期權投資現值來映射其金融期權中的證券市場價值，并按照這一期權距離到期日映射上述人力資本相應金融期權價值的人力資本在職時間，其中，這一在職時間指的是人力資本的期望在職時間。最后，需要說明的是人力資源內在價值映射到金融期權的另一個特性便是其作為期權物質的不確定性，本文將這種不確定性歸納為其作為期權收益的不確定性，從而可獲得企業內部管理以及技術類型人力資本內在期權價值可以表示為：

式（1）中，S、X、t、θ、r分別對應企業人力資源在期權屬性上所產生的預期現金流對應現值、由人力資本映射的金融期權中的證券價值的投資形式現值、人力資本的期望在職時間、各類型人力資本內在價值測度過程中的不確定性、人力資本價值折算過程中不存在風險部分的利率，C刻畫的是上述各要素綜合作用下的人力資本內在價值對應期權價值，由此，可獲得上述人力資本內在期權價值為企業帶來的利益：

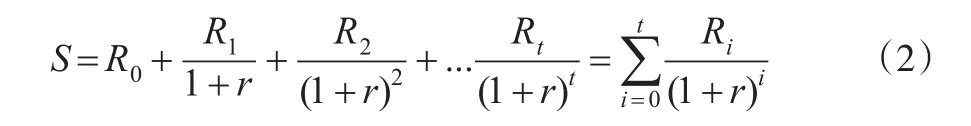
當然，作為為企業帶來利益的人力資本內在價值，其本身存在成本投入的特性，因為研究同樣將涉及企業人力資本內在價值的各個成本因素加以與上述期權內在價值的綜合分析，結合既有研究分析，主要選取企業人力資源的招聘與甄選、內部培訓以及員工薪酬與福利方面支出的成本，將其總和設置為V，由此可以結合上述綜合成本，借助X刻畫的人力資本映射的金融期權中的證券價值的投資形式現值，將其描述為：

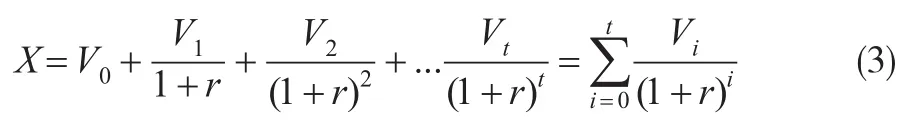
式（1）式（3）中t刻畫的是單獨人力資本也即是具體某類型人力資本（單一類型員工）的期望在職時間，其他參變量描述同上，由此結合式（1）至式（3）可以獲得基于綜合成本的企業人力資本內在價值及其對企業的期權收益，其中，人力資本在履職期間的執行期限映射成距離人力資本自身失去期權價值投資的距離，并以前述式（1）至式（3）中的t表示，人力資本內在價值以及波動期間不確定性仍分別由θ和t表示；企業人力資本在職時間按照期權形態的執行價格進行折算，映射成相關現金流X，而其相應的現金流現值則為人力資本所在企業對應標的資產價值S刻畫，X和S分別映射成的人力資本期權形式折算為：

2 人力資本內在價值的期權定價與價值解析

2.1 人力資本其期權價值解析的分布函數

企業人力資本內在價值存在顯著的金融期權屬性，為此研究結合既有研究中的Black-Scholes模型，進行針對企業人力資本內在價值的期權定價與價值解析，具體描述為：

式（6）中N(x)、t、S分別對應刻畫了參與企業人力資本內在價值折算的樣本正態分布概率累積分布函數、具體某類型人力資本（單一類型員工）的期望在職時間、人力資本所在企業對應標的資產價值的現金流現值；X、C分別對應為某類型人力資本（單一類型員工）所映射的人力資本內在期權價值對應投資成本現值，及其實物期權為企業帶來的價值利益，因此式（6）中的正態分布基期概率分布函數d1可以進一步演化為：

而對應的各累計期概率分布函數可以被表述為：

2.2 面向人力資本內在期權價值的Black-Schloes模型改進

人力資本內在價值映射至企業的實物期權的過程，需要企業進行進一步的決策，而這種決策賦予企業一定程度的物化資本或人力資本的投資抉擇，但同樣性質的期權仍存在不同性質的期權特性，即企業人力資本內在價值存在多期投資特征，無論是從企業的企業人力資源自身的流動還是其在企業內部供職期間所產生的期權現值，都涉及企業為之進行的人員招聘及甄選、內部培訓以及員工薪酬與福利方面都產生相應的疊期成本，而這一成本也不僅構成企業人力資本內在價值的動態期權收益，更是制約每一期人力資本內在價值的期權現值。而從企業管理以及人力資本內在價值期權折現角度而言，也只有任意一期的企業人力資本內在價值完全實現期權現值利益目標，才能進一步適時開展下一期的人力資本內在價值期權折現目標的實施。而這種疊期循環特性的人力資本內在價值期權化利益實現，是以上一期成本目標的有效管理實現，從人力資本的期權價值折算角度則應屬于復合人力資本期權現值，因而其實現是一種映射至企業的實物期權的過程的復合嵌套，具有實物期權形式特征的復合特性。

結合上述分析過程中關于企業人力資本內在價值的疊套復合特性，研究進行了Black-Scholes模型的改進，其中，人力資本內在價值的金融期權現金流映射為累計到期方式，也即是剔除了期權累計過程中生成人力資本期權溢價現金流，并將其后移至各期累計期權現金流中；同時，結合前述關于人力資本內在價值期權折算的成本分析，假定每一期的人力資本存續決策以上一期疊套折算后的期權超過綜合成本為條件，對應的人力資本決策直接結果為人員續用或解聘，由此形成了區別于一般Black-Scholes模型的人力資本內在價值期權折算的疊套方式。

關于人力資本內在價值的疊套性質特征，研究以前期期權執行結果為本期人力資本決策依據，為此將這一決策依據歸納為當期人力資本期權屬性綜合特征，并將其用Π(t)表示，則上述分析中的期權疊套映射到企業人力資本期權價值可以表述為基于第T+i期的期望現金流，即：

由此綜合式（7）至式（8）可獲得以下關于改進Black-Scholes測度的企業人力資本內在價值疊套期權折算表達式，即：

式（10）中，dn刻畫的是上述具備疊套特征的企業人力資本內在價值經過多次循環疊套的累積跳躍，由于需要配合前述的中間過程的人力資本期權價值剔除，為此，研究以S(t)刻畫每次跳躍過程所對應的期權價值，而疊套過程同樣存在前期人力資本期權價值的遞增或衰減變動，為此，研究將疊套過程中非剔除部分的人力資本期權價值歸納為S(t±i)，S(t)、S(t±i)對應的最終累積人力資本期權價值被定義為兩式對應在第T時序值。

2.3 改進Black-Scholes模型對企業人力資本內在價值期權估計實施步驟

研究給予改進Black-Scholes模型的人力資本期權動態現金流價值，即賦予每層次人力資本期權基期價值的折算方式，當企業運營過程中的人力資本期權價值外部干擾因素充足或足以影響當期人力資本期權現金流時，設定一個包含λ參數的泊松隨機過程，且其對應的當層期權現金流受到復合參變量共同作用，即受到企業人力資本內在價值期權層進的疊套方向與疊套力度的決定，前者映射至企業人力資本內在期權價值現金流的增減趨勢，而后者映射至人力資本價值的期權變動程度，兩者交積則構成企業人力資本期權價值由層級疊套向定向跳躍的邁進，并預先為這種跳躍設定一個隨機參變量λt；而當人力資本期權價值外部干擾因素不足以影響當期人力資本期權現金流時，對其對應更多當層期權現金流設定為基期無風險實物期權折算。

對應的可獲得預定目標效應的人力資本期權投資成本現值可以被刻畫成基于前述隨機參變量，以及分段分布特征函數：

其次，針對上述折算過程進行由層級疊套向定向跳躍的發生頻度、程度折算，此時，需設定一個動態參變量變動的到達界定參數λ，即判定企業人力資本期權價值現金流層級疊套是否達到跳躍的程度，λ為前述式中的泊松隨機參數，由此可獲得上述具備疊套特征的企業人力資本內在價值經過多次循環疊套的累積跳躍dn的隨機部分，根據對于疊套行為的分析，研究設定φt為人力資本期權與現值的比例，當且僅當層進疊套指示信號為零時，不存在單一層次的人力資本疊套或跳躍行為，那么此時的企業人力資本內在期貨現金流價值可被表述為：

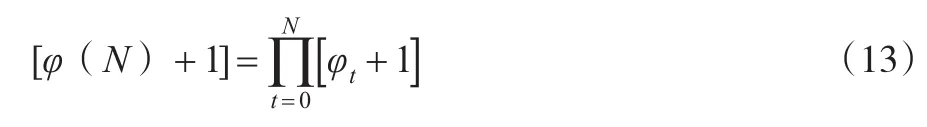
式（13）中，φt這一動態參變量表示各層級企業人力資本內在期貨價值彼此獨立，并設定其初始值為零；且企業人力資本期權價值現金流層級疊套達到跳躍的程度臨界影響因素由 φt|Xt來刻畫，其形成了幅度為φt的人力資本期權價值基于改進Black-Scholes模型層級的跳躍。

根據上述分析，φt|Xt服從于上述瑞利分布，φt|Xt這一隨機二維向量的企業人力資本內在價值二分量具備獨立同方差的正態分布的分段分布特征，研究可以根據式（9）至式（13）進一步獲取對應企業人力資本內在價值期權動態疊套折算的函數特征指標，其方差和均值分別為：

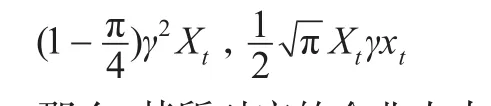
那么，其所對應的企業人力資本內在價值期權疊套折算模型可以歸納為：

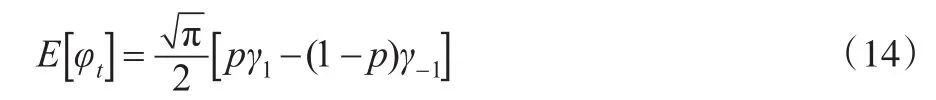
其中，γ1、γ-1和 p、1-p分別對應為人力資本作為期權價值發生現金流累積過程中的層級正負向性的跳躍及其發生跳躍行為的概率，式（10）在改進Black-Scholes模型下可被表述為：

這里研究主要將前述關于人力資本期權價值現金流累積方式的層級疊套折算跳躍行為的臨界風險加以細化分析，即任何在層級疊套過程中發生的期權現金流跳躍也存在一定的風險，而并非簡單的無風險假設，從而以式（15）中的零均值的維納過程加以解釋，該過程的正態分布方差仍為dt。

3 企業人力資本內在價值期權估計實證驗證

3.1 企業人力資本內在期權價值隨機最優控制

根據上述分析，研究利用算例進行企業人力資本內在價值期權折算。具體過程如下：

首先，利用期權價格的隨機最優控制作為區間問題進行折算。設定人力資本以金融期權形式累積過程的上下限分別為V+(S，t)、V-(S，t)，借助區間控制函數u(t)=r(t)形成針對前述式（10）、式（15）改進的疊套層進跳躍行為期權現金流累積狀態方程：

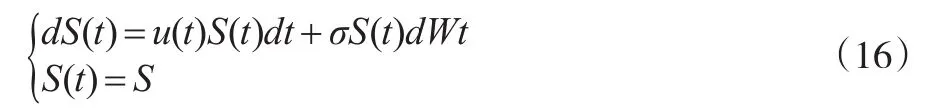
其中區間控制函數的控制集為：

該控制集必須確保在疊套層級幅度中全區可測，即具備一個全區可測集：

結合式（10）、式（14）構成基于人力資本內在期權價值指標關系的性能指標泛函數：

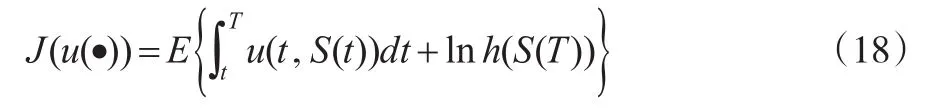
將人力資本內在期權價值疊套層級跳躍行為歸納為對于包含區間跳躍最優上下限控制集和最優控制函數uˉ(·)的測度模型：

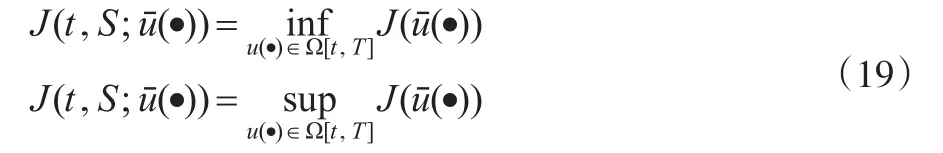
3.2 基于改進Black-Scholes模型的企業人力資本內在期權復合評價

根據上述分析，以疊套層級進行人力資本在企業內部期權屬性變遷的區間劃分，其對應的實際區間為招聘甄選期t0、進企直至被錄用期t1、在職培訓期T0

結合前述分析，將這一具備疊套層級跳躍的人力資本內在期權折算簡化為：

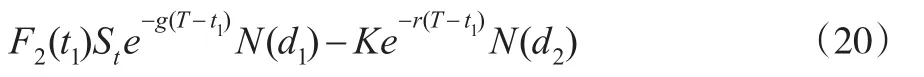
上述各疊套跳躍期間的期望值為：

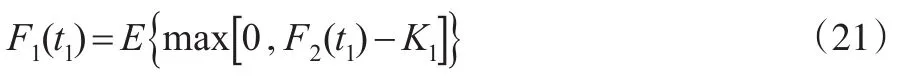
E作為期望算子，服從條件：

最后，針對人員在招聘甄選期、進企直至被錄用期、在職培訓期設定全區的人力資本期權現金流綜合成本決策行為為第t0期，由此可獲得具體疊套層級區間的點狀人力資本內在期權價格折線為：

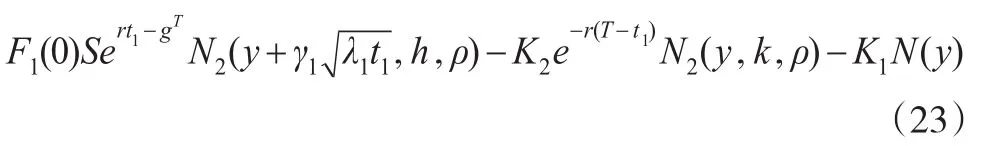
3.3 算例驗證

某市高新區內生物技術公司，企業配備齊全的工種，并且具備獨立人力資源部門。研究通過對該企業技術類型員工的樣本選取，并依據該企業自2011—2014年的員工業績考核數據，進行業績加權平均，獲得如表2所示的該企業人力資本工作績效評估。

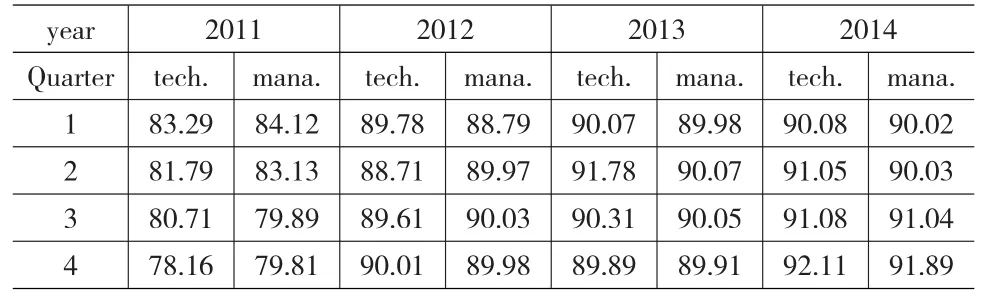
表2 企業人力資本內在價值樣本分類業績評估

接著，研究細化企業人力資本內在價值期權測度，并在結合2011—2014年對應員工工作業績折算4年員工業績加權平均值的基礎上，進行期權資本價值波動率的折算，具體折算結果如表3所示。

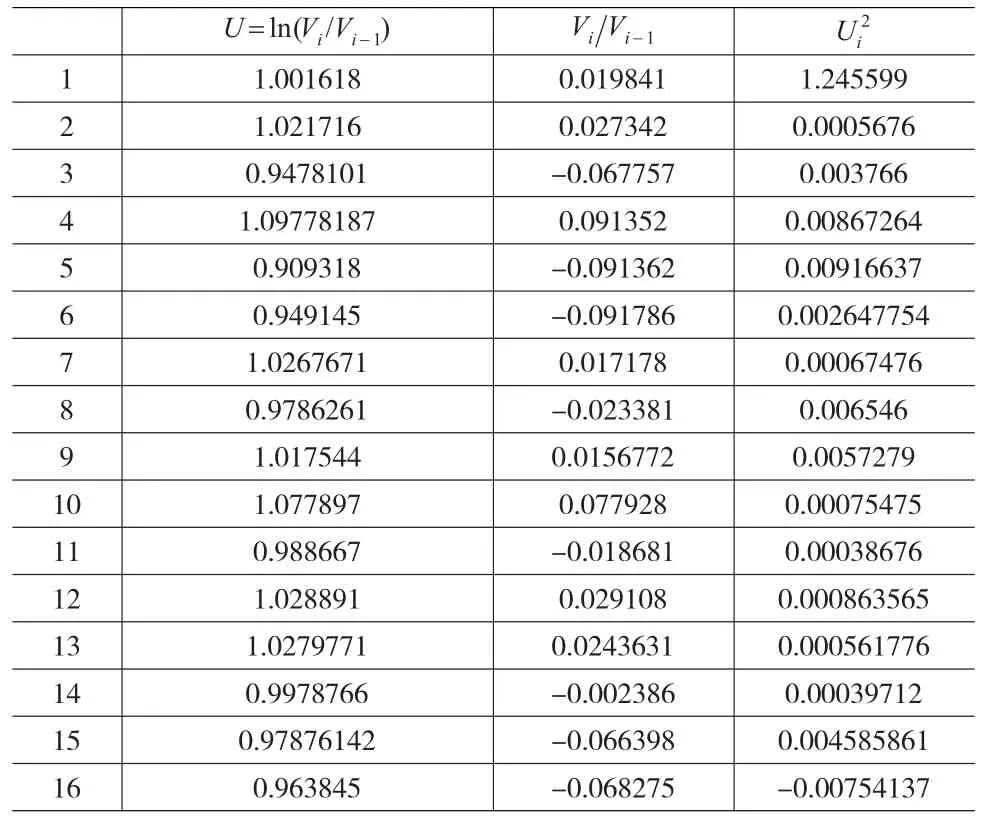
表3 人力資本業績加權評級基礎上的期權資本價值波動率折算

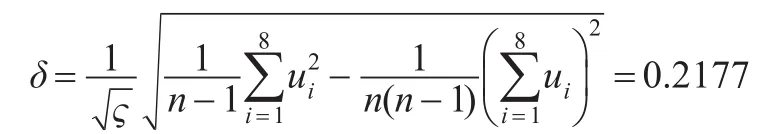
其中?為樣本觀測值倒數的時間間隔。

該企業針對員工的福利主要由以下幾部分構成：

每年人員招聘廣告費用為5萬元人民幣，住房津貼共計9萬元，人員工資支付為7萬元每年，對應培訓費為4萬元每年，r=0.1，t=3，則結合式（5）、式（13）可獲得疊套層級投資綜合成本為：

同時，根據前述分析技術類負責經營層人力資本的收益為可以表述為：

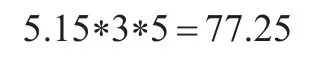
則在結合式（16）基礎上，推算人力資本收益各跳躍期期權的微分現值為：

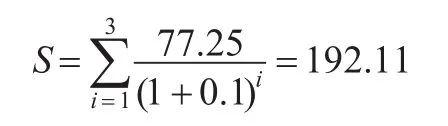
根據前述則可獲得最終基于改進Black-Scholes模型的各項數值為S=192.11，X=110.98，δ=21.77%，經式（7）計算可得：

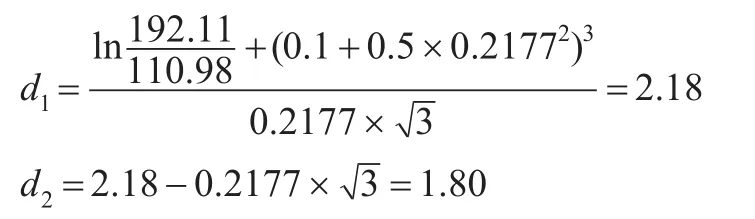
從算例驗證結果來看，存在疊套和跳躍的超過了包含津貼、工資以及內部培訓費用在內的20萬元，因此經過改進Black-Scholes模型測算，可以獲知這一類型的人力資本投入對于企業期權性質的投資具有持續意義。

4 總結

研究在結合當前企業人力資本內在價值評估研究的基礎上，根據企業人力資本流動特征，以改進Black-Scholes模型的方法進行了針對于疊套行為特征的人力資本期權價值跳躍層級變動的評估研究。從人員招聘及甄選、內部培訓等角度構建綜合成本，并按照跳躍行為的臨界判斷作為企業人力資本期權價值累積的基礎，進行了相應的人力資本期權價值折算。驗算結果表明，改進Black-Scholes模型對于具備期權現金流映射價值疊套跳躍特性的人力資本評估存在較好的解釋能力，在企業存在更為顯著的人力資源動態調整期間的期權價值預測中，需要結合綜合投入成本進行相應的人力資本期權價值估計。

[1]Ekstr?m E，Tysk J.The Black–Scholes Equation in Stochastic Vola?tility Models[J].Journal of Mathematical Analysis’s&Sapplications， 2010，(2).

[2]Jarrow R A，Protter P，Shimbo K.Asset Price Bubbles in Incomplete Markets[J].Mathematical Finance，2010，(2).

[3]Muthuraman K.A Moving Boundary Approach to American Option Pricing[J].Journal of Economic Dynamics&Control，2008，(11).

[4]王艷培，劉繼春.多個資產期權的泡沫和Black-Scholes方程[J].廈門大學學報:自然科學版，2014，(6).

[5]李洋，楊舒雅.最優資本結構選擇與例證——基于權衡理論與Black-Scholes期權定價模型[J].財會通訊，2015，(1).

[6]任智格，何朗，黃樟燦.一種無風險利率時變條件下的Black-Scho?les期權定價模型[J].數學雜志，2015，(1).

[7]呂喜明，韓燕.基于MATLAB的Black-Scholes-Merton歐式期權定價模型的計算研究[J].經濟論壇，2013，(6).

[8]景珮，李秀芳.我國財產保險公司資本結構的影響因素分析——基于權衡理論視角的實證檢驗[J].現代財經：天津財經大學學報， 2013，(1).

（責任編輯/浩 天）

C976.8

A

1002-6487（2016）21-0178-04

四川石油天然氣發展研究中心基金項目（石油企業人力資本價值鏈研究）（川油氣科SKW14-01）

廖特明（1970—），男，四川鄰水人，碩士，副教授，研究方向:人力資源管理。

譚志勇（1982—），男，湖北咸寧人，博士研究生，研究方向：人力資源管理