參數(shù)法、半?yún)?shù)法的動(dòng)態(tài)VaR模型風(fēng)險(xiǎn)度量

張 瓊，黃旭東，林雪勤

（1.安徽師范大學(xué)a.經(jīng)濟(jì)管理學(xué)院;b.數(shù)學(xué)計(jì)算機(jī)科學(xué)學(xué)院,安徽蕪湖241000；2.國泰安教育技術(shù)股份有限公司，合肥230088）

參數(shù)法、半?yún)?shù)法的動(dòng)態(tài)VaR模型風(fēng)險(xiǎn)度量

張 瓊1a，黃旭東1b，林雪勤2

（1.安徽師范大學(xué)a.經(jīng)濟(jì)管理學(xué)院;b.數(shù)學(xué)計(jì)算機(jī)科學(xué)學(xué)院,安徽蕪湖241000；2.國泰安教育技術(shù)股份有限公司，合肥230088）

文章采用參數(shù)法和半?yún)?shù)法，分別考慮標(biāo)準(zhǔn)化收益在GED、SGT、GPD分布下以及FSH方法下的GARCH模型、EGARCH模型和PGARCH模型的風(fēng)險(xiǎn)測(cè)度的準(zhǔn)確性，據(jù)此組建了12種風(fēng)險(xiǎn)測(cè)度的動(dòng)態(tài)VaR模型，并采用道瓊斯股票市場(chǎng)指數(shù)和上證指數(shù)進(jìn)行實(shí)證分析。對(duì)收益率進(jìn)行基本統(tǒng)計(jì)分析發(fā)現(xiàn)兩個(gè)股票市場(chǎng)的收益率都不服從一般的正態(tài)分布。運(yùn)用后驗(yàn)測(cè)試的方法，對(duì)所有模型的樣本外預(yù)測(cè)動(dòng)態(tài)VaR值采用LR、LRuc和DQ三種方法綜合檢驗(yàn)，并由損失函數(shù)值可以看出：GARCH模型的風(fēng)險(xiǎn)度量能力最弱，在置信水平99.5%下，EGARCH模型最準(zhǔn)確，在置信水平95%下，PGARCH模型最準(zhǔn)確；GED分布描述市場(chǎng)的準(zhǔn)確程度相對(duì)最弱，在較高的置信水平下，半?yún)?shù)模型能更好地度量市場(chǎng)的風(fēng)險(xiǎn)，在較低的置信水平下，參數(shù)模型能更好地度量股票市場(chǎng)的風(fēng)險(xiǎn)。

動(dòng)態(tài)VaR模型；風(fēng)險(xiǎn)測(cè)度；損失函數(shù)

0 引言

做好風(fēng)險(xiǎn)管理，最重要的一個(gè)環(huán)節(jié)是進(jìn)行風(fēng)險(xiǎn)度量，金融風(fēng)險(xiǎn)度量的主要手段之一是在險(xiǎn)價(jià)值(Value at Risk, VaR)。VaR可以看作是建立在過去和現(xiàn)在信息上的未來投資組合的分位數(shù)，由于投資組合的收益分布隨時(shí)間在變化，如何準(zhǔn)確的估計(jì)VaR，在實(shí)踐中是一個(gè)很大的挑戰(zhàn)。估算VaR方法主要有參數(shù)法、半?yún)?shù)法和非參數(shù)法。

在參數(shù)法中，GARCH模型是應(yīng)用最為廣泛的時(shí)間序列波動(dòng)率模型，然而在GARCH模型應(yīng)用中，基礎(chǔ)的研究通常假設(shè)資產(chǎn)收益服從正態(tài)分布，而大量的實(shí)證分析表明資產(chǎn)收益表現(xiàn)出非對(duì)稱性、厚尾、尖峰等特征，因此假設(shè)服從正態(tài)分布來估計(jì)投資組合的動(dòng)態(tài)VaR，對(duì)于風(fēng)險(xiǎn)管理者來說，不能產(chǎn)生好的預(yù)測(cè)結(jié)果，常常嚴(yán)重低估風(fēng)險(xiǎn)。如徐煒和黃炎龍(2008)比較研究GARCH族的11種模型分別在正態(tài)分布和Skewed-t分布下度量動(dòng)態(tài)VaR值的精確程度，結(jié)果表明Skewed-t分布較好地?cái)M合了金融資產(chǎn)的厚尾特性，Cheng和Hung(2011)在GARCH模型中比較了正態(tài)分布、t分布、SSD和GED下的動(dòng)態(tài)VaR，結(jié)論是假設(shè)服從SSD和GED下的動(dòng)態(tài)VaR得出的結(jié)論最好。Polanski和Stoja (2010)比較了正態(tài)分布、t分布、SGT和EGB2分布，發(fā)現(xiàn)僅后兩種分布提供了精確的動(dòng)態(tài)VaR估計(jì)。

半?yún)?shù)方法主要是將非參數(shù)和參數(shù)法結(jié)合。在非參數(shù)法中，最典型的就是歷史模擬法，Trenca(2009)等結(jié)論表明單純使用歷史模擬法對(duì)于估計(jì)VaR不準(zhǔn)確，歷史模擬法常常會(huì)低估風(fēng)險(xiǎn)，并且對(duì)于一些重大事件的靈敏性比較低。Barone-Adesi等(1999)提出的一種半?yún)?shù)方法：FSH (Filtered Historical Simulation)方法，即將歷史模擬法和條件波動(dòng)率模型相結(jié)合。Marimoutou等(2009)認(rèn)為FSH繼承了歷史模擬法優(yōu)勢(shì)的同時(shí)提高了模型的靈敏度。Zikovic等(2009)的研究表明FSH方法的預(yù)測(cè)效果比歷史模擬法優(yōu)越很多。應(yīng)用極值理論方法（EVT）考慮尾部分布所具有的特征和市場(chǎng)極端變動(dòng)有密切關(guān)系是另一種半?yún)?shù)方法，極值理論方法不對(duì)金融收益整體分布進(jìn)行建模，僅考慮分布的尾部特質(zhì)。高瑩等(2008)將基于極值理論的GARCH-EVT模型與普通的GARCH-NORMAL模型進(jìn)行比較，結(jié)果表明GARCH-EVT模型優(yōu)于GARCH-NORMAL模型。Bekiros和Georgoutosos(2005)指出在較高置信水平下，EVT理論體系對(duì)于極端事件損失的預(yù)測(cè)最準(zhǔn)確。

近年來，已有學(xué)者在不同置信水平下研究不同模型的準(zhǔn)確性，如葉青（2000）引入基于GARCH模型的方差協(xié)方差法和David Li提出的半?yún)?shù)法對(duì)中國的股票市場(chǎng)進(jìn)行了模擬。Chen等(2013)比較了不同置信水平下不同方法計(jì)算的VaR值的準(zhǔn)確性。然而對(duì)于GARCH族模型下，利用參數(shù)法和半?yún)?shù)法在不同置信水平下對(duì)動(dòng)態(tài)VaR模型的準(zhǔn)確性進(jìn)行比較的文獻(xiàn)相對(duì)較少,且用兩種不同市場(chǎng)的數(shù)據(jù)同時(shí)實(shí)證分析，得到的結(jié)果顯然更具說服力。

因此本文基于三種有代表性的GARCH模型(GARCH、EGARCH、PGARCH)的參數(shù)與半?yún)?shù)動(dòng)態(tài)VaR模型，考慮標(biāo)準(zhǔn)化收益在GED、GPD、SGT分布下以及FSH方法下，探究在不同置信水平下，動(dòng)態(tài)VaR模型預(yù)測(cè)的靈敏度，從而找到最優(yōu)預(yù)測(cè)模型，為金融市場(chǎng)的風(fēng)險(xiǎn)測(cè)度提供合適的度量工具。

1 動(dòng)態(tài)VaR模型的定義及其估計(jì)

1.1 動(dòng)態(tài)VaR模型的定義

VaR是指在給定的概率α下，在某一段時(shí)期內(nèi),預(yù)測(cè)投資組合的最大損失值，也是投資組合收益分布的特定分位數(shù)的估計(jì)，數(shù)學(xué)表達(dá)式為：

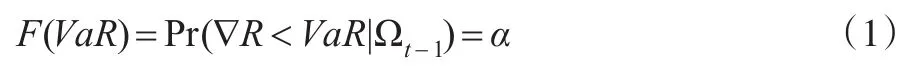
其中F(·)是投資資產(chǎn)組合收益的分布，?R是某一段時(shí)期內(nèi)投資組合值。VaR按是否考慮波動(dòng)率的時(shí)變性，分為靜態(tài)VaR和動(dòng)態(tài)VaR，靜態(tài)VaR是沒有考慮波動(dòng)率的時(shí)變性，只是由前一時(shí)間段的整體波動(dòng)率來預(yù)測(cè)下一刻的波動(dòng)率。而動(dòng)態(tài)VaR考慮了波動(dòng)率的時(shí)變和股票收益序列的波動(dòng)集群性，下一刻的波動(dòng)率由前一時(shí)刻的波動(dòng)率來預(yù)測(cè)，有更好地準(zhǔn)確性和及時(shí)性。

動(dòng)態(tài)VaR模型的表達(dá)式為：

故在給定置信水平1-α情況下，對(duì)于式(2)，主要由兩部分組成，一是波動(dòng)率（即條件均值和條件方差）；二是θ，即標(biāo)準(zhǔn)化收益的分位數(shù)。

動(dòng)態(tài)VaR模型中對(duì)于波動(dòng)率GARCH模型和θ值的確定都需要知道標(biāo)準(zhǔn)化收益zt的值或者zt服從的分布，本文的研究假定zt服從GED、SGT、GPD分布，將資產(chǎn)收益數(shù)據(jù)進(jìn)行中心化得到條件標(biāo)準(zhǔn)化收益zt，利用最大似然法估計(jì)出zt在不同分布下GARCH、EGARCH和PGARCH三個(gè)模型中的未知參數(shù)，然后又采用FSH方法對(duì)三個(gè)模型的未知參數(shù)作出估計(jì)。

1.2 動(dòng)態(tài)VaR模型波動(dòng)率的估計(jì)

GARCH模型是反映金融市場(chǎng)時(shí)變特征最常用的波動(dòng)率模型，它能有效捕捉股市的叢集性效應(yīng)、非對(duì)稱特征等。

GARCH族模型有多種不同類型的表達(dá)形式，其中最具有代表性的是GARCH(1,1)、EGARCH和PGARCH三個(gè)模型。

Bollerslev在1986年提出的線性對(duì)稱GARCH(1,1)模型，具體表達(dá)式為：

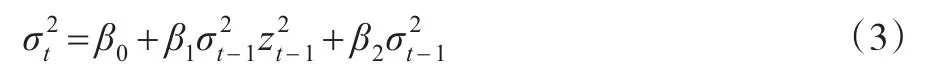
Nelson在1991年提出指數(shù)形式的GARCH模型(EGARCH模型)，模型的表達(dá)式為：

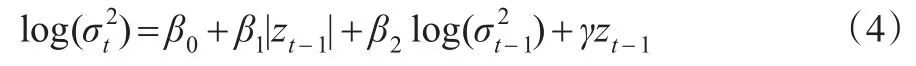
模型中條件方差采用對(duì)數(shù)形式，即使參數(shù)為負(fù)數(shù)，條件方差也是正的，這就規(guī)避了參數(shù)都為正的條件。若γ≠0時(shí)，說明信息作用非對(duì)稱。

PGARCH模型是對(duì)GARCH模型作了進(jìn)一步的擴(kuò)展，對(duì)標(biāo)準(zhǔn)差的冪次進(jìn)行模擬，這個(gè)冪并不需要事先給定，而是通過模型自身來決定。它的形式為：則模型是對(duì)稱的；反之不對(duì)稱。E(zt)=0，VaR(zt)=1，限制條件為 β0＞0,0≤β1＜1,0≤β2＜1。

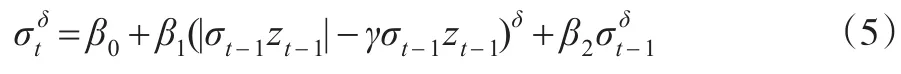
這里的μt和σt是建立在Ωt-1={rt-1，rt-2，…}上的條件均值和條件標(biāo)準(zhǔn)差

1.3 動(dòng)態(tài)VaR模型θ值的估計(jì)方法

估計(jì)標(biāo)準(zhǔn)化收益zt的分位數(shù)θ，需要先知zt的整個(gè)分布或部分分布。

（1）參數(shù)法

在傳統(tǒng)的研究中，常常假設(shè)zt服從標(biāo)準(zhǔn)正態(tài)分布，但是在實(shí)踐中我們發(fā)現(xiàn)即使對(duì)于標(biāo)準(zhǔn)化收益的分布仍然有尖峰、厚尾等特征，需要對(duì)zt的分布作出新的假設(shè)。

GED(Generalised Error Distribution)分布是Newey在1991年提出，其密度函數(shù)的表達(dá)式為：

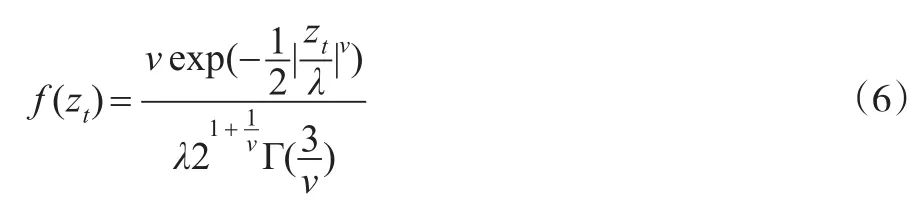
SGT(the Skewed Generalized T Distribution)分布是由Theodossiou在1998年提出的，標(biāo)準(zhǔn)化收益zt的SGT分布的密度函數(shù)表達(dá)為：

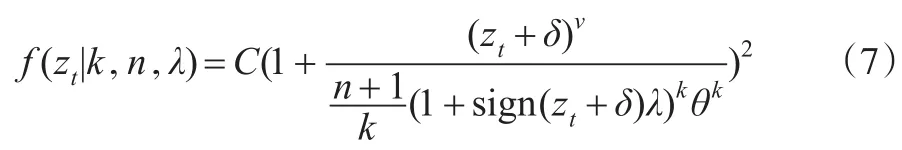
其中sign是符號(hào)函數(shù)；λ是偏度參數(shù)，且|λ|＜1；正數(shù)k和n是尖峰參數(shù)，且B(·)是 Beta函數(shù)。

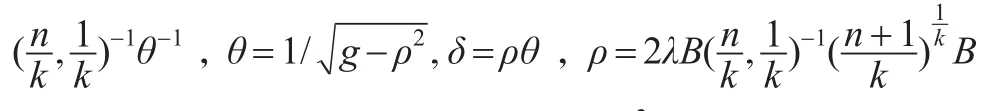
（2）半?yún)?shù)法

Barone-Adesi等(1999)對(duì)于標(biāo)準(zhǔn)化收益分布的刻畫提出了一種半?yún)?shù)模型，即FSH(Filtered Historical Simulation)模型。此模型是非參數(shù)和參數(shù)方法的一種結(jié)合，利用歷史模擬法來模擬標(biāo)準(zhǔn)化收益的分布，然后將歷史模擬法得到的數(shù)據(jù)特征（如捕捉金融數(shù)據(jù)的厚尾、偏態(tài)等非正常特征）和GARCH模型相結(jié)合，從而估計(jì)出標(biāo)準(zhǔn)化收益的分布。

另一種半?yún)?shù)法是依據(jù)條件極值理論(Extreme Value Theory，EVT)進(jìn)行估計(jì)。首先，定義超過閾值u分布的條件概率函數(shù)為：

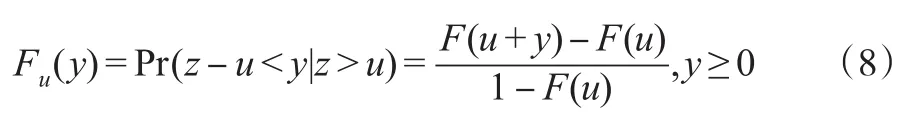
Balkerma等(1974)指出GPD(Generalised Pareto Distribution)是Fu(y)的極限分布,并且論證了當(dāng)閾值u足夠大時(shí)，F(xiàn)u(y)=Gξ，σ(u)(y)。

這里的Gξ，σ(u)(y)表示服從GDP分布，具體表達(dá)式為：

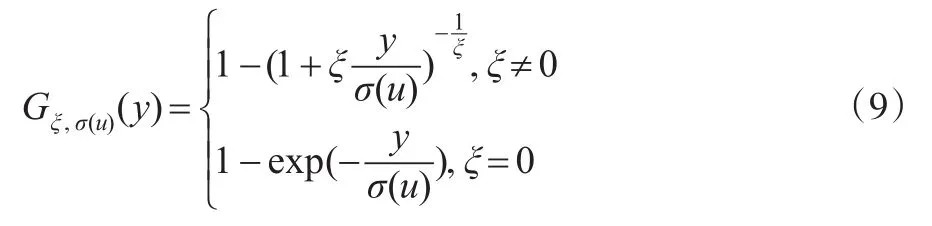
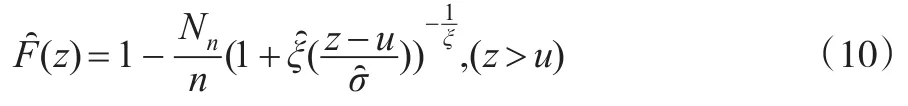
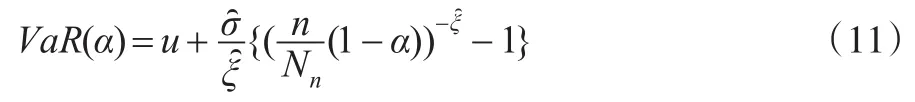
2 動(dòng)態(tài)VaR模型風(fēng)險(xiǎn)測(cè)度準(zhǔn)確性的度量

2.1 動(dòng)態(tài)VaR模型的可行性檢驗(yàn)

對(duì)于動(dòng)態(tài)VaR模型預(yù)測(cè)能力的可行性檢驗(yàn)，主要運(yùn)用回測(cè)檢驗(yàn)的方法，本文采用非條件覆蓋似然比率檢驗(yàn)(the LR of Unconditional Coverage testing)、條件覆蓋似然率檢驗(yàn)(the LR of conditional Coverage test)和條件分位數(shù)回歸檢驗(yàn)(the Dynamic Quantile test)這三個(gè)檢驗(yàn)來綜合判斷，一個(gè)準(zhǔn)確的模型均應(yīng)該通過這些檢驗(yàn)。

對(duì)于異常事件通常有如下描述，將預(yù)測(cè)第t+1天的動(dòng)態(tài) VaRt+1(α)與當(dāng)日投資組合 rt+1進(jìn)行比較，若rt+1＜VaRt+1(α)，則稱異常事件出現(xiàn)。則定義異常指標(biāo)變量如下：

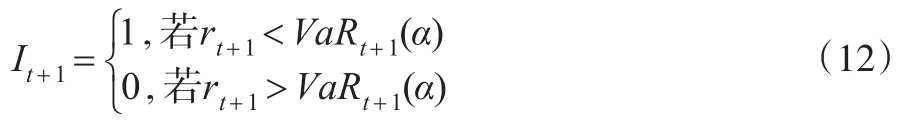
非條件覆蓋似然比率檢驗(yàn)(簡(jiǎn)記LRuc)是Kupiec(1995)建立的，這個(gè)檢驗(yàn)是假設(shè)小于動(dòng)態(tài)VaR(α)的觀測(cè)值的實(shí)際個(gè)數(shù)和期望值是相等的，即原假設(shè)與備擇假設(shè)分別是：似然檢驗(yàn)統(tǒng)計(jì)量為：

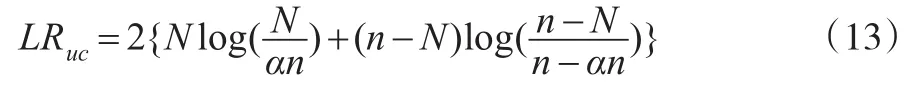
條件覆蓋似然率檢驗(yàn)（簡(jiǎn)記LRcc）是Christoffersen (1998)提出的，指出動(dòng)態(tài)VaR估計(jì)可以看作是金融收益分布在較低尾部的區(qū)間預(yù)測(cè)。此檢驗(yàn)是一種聯(lián)合檢驗(yàn)，即①是否②It+1是否獨(dú)立同分布。LRcc檢驗(yàn)的原假

其中：

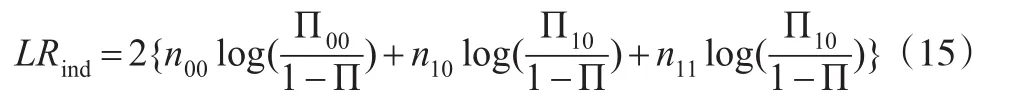
nij是It=i時(shí)It+1=j出現(xiàn)的個(gè)數(shù)，t=1,2,…,n-1。相應(yīng)地依據(jù)此檢驗(yàn)，可以判定當(dāng)產(chǎn)生過多或者過少的聚類異常事件時(shí)，拒絕動(dòng)態(tài)VaR模型。

自信息技術(shù)出現(xiàn)以后，憑借著出眾的性能與能力，信息技術(shù)成功的被應(yīng)用到人類社會(huì)發(fā)展的方方面面。信息技術(shù)不僅改變了人們對(duì)生活工作的看法，同時(shí)也提高了人們的生活學(xué)習(xí)質(zhì)量。尤其是在教育系統(tǒng)當(dāng)中，信息技術(shù)的出現(xiàn)更是有著豐富教育資源，實(shí)現(xiàn)教育公平，不受時(shí)間地域限制的線上教育等功能和優(yōu)勢(shì)。成人教育是我國教育系統(tǒng)中一項(xiàng)非常重要的教育，和全日制教育有著不同的教育形式和教學(xué)形式。是幫助成人取得專業(yè)資格、提高技術(shù)、豐富知識(shí)、增長(zhǎng)能力的重要途徑。因很多成人缺少足夠的時(shí)間參與課堂學(xué)習(xí)，因此信息技術(shù)在成人教育中有著重大潛力，這就要求成人教育教師必須要掌握信息教育素質(zhì)。

條件分位數(shù)回歸檢驗(yàn)(簡(jiǎn)記為DQ檢驗(yàn))由Engle和Manganelli(2004)提出，基本原理為當(dāng)動(dòng)態(tài)VaR已估計(jì)，檢驗(yàn)異常事件指標(biāo)和屬于Ωt-1的所有變量是否相關(guān)。首先定義一個(gè)序列變量指標(biāo)函數(shù)：

其中I(·)是示性函數(shù)，1-α是給定的置信水平。Engle和Manganelli(2004)提出一個(gè)優(yōu)的模型應(yīng)該產(chǎn)生一系列無偏性、無相關(guān)性Hit，并且Hit的期望為0，因此DQ檢驗(yàn)同時(shí)檢驗(yàn)兩個(gè)方面內(nèi)容：①E(Hitt)=0；②Hitt是互不相關(guān)的。這兩個(gè)檢驗(yàn)內(nèi)容通過下列回歸進(jìn)行檢驗(yàn)：

其中X=(1，Hitt-1，Hitt-2，…，Hitt-p，X1，…，Xq)，B=(β0，β1，…，βp+q)T,Xj是屬于Ωt-1的解釋變量。檢驗(yàn)的原假設(shè)H0∶B=0。在原假設(shè)基礎(chǔ)上的條件分位數(shù)檢驗(yàn)統(tǒng)計(jì)量為：

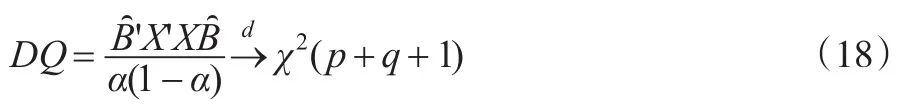
2.2 動(dòng)態(tài)VaR模型風(fēng)險(xiǎn)估計(jì)準(zhǔn)確程度的度量

對(duì)于風(fēng)險(xiǎn)管理者來說，關(guān)注的不僅僅是異常事件是否發(fā)生，更關(guān)注當(dāng)異常事件發(fā)生后損失的大小，因?yàn)閾p失的大小和金融機(jī)構(gòu)儲(chǔ)備金多少有直接關(guān)系。Lopez(1998)提出利用損失函數(shù)作為評(píng)估異常事件發(fā)生后產(chǎn)生的后果，主要考察當(dāng)異常事件發(fā)生時(shí)，觀察值rt與預(yù)測(cè)的動(dòng)態(tài)VaRt之間的距離，包含了異常事件發(fā)生的次數(shù)和損失大小。表達(dá)式為：

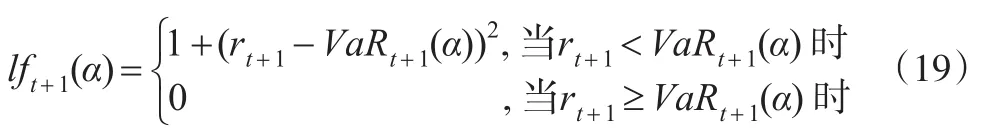
對(duì)于動(dòng)態(tài)VaR模型的優(yōu)劣，可通過lf的大小表現(xiàn)出來，所以當(dāng)一個(gè)模型的lf值小于另一個(gè)，這個(gè)模型便優(yōu)于后者。

3 實(shí)證分析

實(shí)證分析的數(shù)據(jù)選取了中國股票市場(chǎng)的上證指數(shù)和美國股票市場(chǎng)的道瓊斯指數(shù)。

道瓊斯指數(shù)選用了1991年1月2日到2013年12月30日的收盤指數(shù)(共5294個(gè)樣本)作為實(shí)證分析的數(shù)據(jù)，中國的上證指數(shù)選用了2012年2月20日到2014年11月7日的每日收盤指數(shù)(共660個(gè)樣本)作為實(shí)證分析的數(shù)據(jù)，所有的數(shù)據(jù)來源于國泰安數(shù)據(jù)庫。

3.2 股指對(duì)數(shù)收益率的統(tǒng)計(jì)特征

表1 道瓊斯指數(shù)(1991/1/2-2013/12/30)描述性統(tǒng)計(jì)

由表1可以看出，道瓊斯股票指數(shù)的每日對(duì)數(shù)收益指數(shù)JB=16977.66＞5.3995，JB對(duì)應(yīng)的概率P=0.00＜0.05，說明金融收益序列不服從正態(tài)分布。且偏度S=-0.153461＜0，則說明序列分布左尾比右尾密集，峰度K=11.37894＞3,，則說明此序列的分布比正態(tài)分布的峰部更尖。

作出上證綜合指數(shù)的對(duì)數(shù)收益率基本統(tǒng)計(jì)分析的時(shí)間序列圖、分布圖、核密度圖和Q-Q圖，如圖1所示。

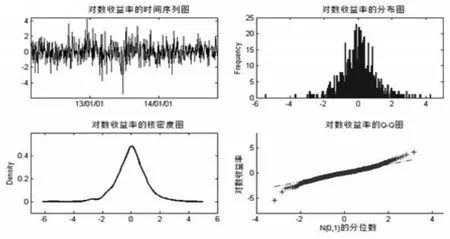
圖1上證指數(shù)對(duì)數(shù)收益率的基本統(tǒng)計(jì)分析圖

圖1 直觀的展現(xiàn)了我國股票市場(chǎng)對(duì)數(shù)收益率的一些特性。由分布圖和核密度估計(jì)圖可以觀察到我國對(duì)數(shù)收益率左偏并且有很高的峰度；Q-Q圖上的點(diǎn)在兩端處明顯偏離所示直線，可見上證綜合指數(shù)收益率不服從正態(tài)分布。

對(duì)兩個(gè)不同的股票市場(chǎng)的收益率進(jìn)行基本統(tǒng)計(jì)分析發(fā)現(xiàn)，兩個(gè)市場(chǎng)的收益率都不服從一般的正態(tài)分布。

3.3 模型的參數(shù)和動(dòng)態(tài)VaR值估計(jì)

對(duì)于道瓊斯指數(shù)，本文選用1991—2000年的數(shù)據(jù)作為前段數(shù)據(jù)，估計(jì)出條件均值-方差模型以及標(biāo)準(zhǔn)化收益的分布函數(shù)的未知參數(shù)。然后用2001年的數(shù)據(jù)來評(píng)估模型的好壞，即假設(shè)2001年的條件均值-方差滿足前10年估計(jì)出來模型，并且分布函數(shù)在2001年不變。利用2000/12/ 29(2000年交易最后一天數(shù)據(jù))估計(jì)2001/1/2(即2001年交易第一天)條件均值-方差，再利用2001/1/2真實(shí)收益數(shù)據(jù)和條件均值-方差，預(yù)測(cè)出2001/1/3的條件均值-方差，以此類推，得到2001年每天條件均值-方差。接著利用前十年已估計(jì)概率分布得到不同模型對(duì)應(yīng)的分位數(shù)θ，對(duì)伴隨概率α取不同的值,在本文中伴隨概率取0.5%、1%、2.5%和5%，由式(2)算得不同模型基于滾動(dòng)樣本上2001年每天的VaR估計(jì)值，根據(jù)式(12)異常事件的定義，統(tǒng)計(jì)出相應(yīng)模型中異常事件的個(gè)數(shù)。再接著剔除1991年數(shù)據(jù)，加入2001年實(shí)際收益數(shù)據(jù),同上面的做法求得2002年的動(dòng)態(tài)VaR值和對(duì)應(yīng)的異常值個(gè)數(shù),同理一直滾動(dòng)求解出后面的年份的動(dòng)態(tài)VaR值和對(duì)應(yīng)的異常值個(gè)數(shù),直到2013年,運(yùn)用每10年的滾動(dòng)樣本，分別產(chǎn)生了12個(gè)不同模型后13年評(píng)估的VaR值和異常值個(gè)數(shù)，得到3269個(gè)動(dòng)態(tài)VaR值的評(píng)估數(shù)據(jù)。

對(duì)于上證指數(shù)，本文選用了2012/2/20—2013/3/14的數(shù)據(jù)作為觀測(cè)樣本，以前220個(gè)交易日數(shù)據(jù)作為前段數(shù)據(jù)估計(jì)出條件均值-方差模型，以及標(biāo)準(zhǔn)化收益的分布函數(shù)的未知參數(shù)。然后用接下來40個(gè)交易日的數(shù)據(jù)進(jìn)行檢驗(yàn)。同道瓊斯指數(shù)的估計(jì)方法，對(duì)12種模型分別產(chǎn)生了440個(gè)的評(píng)估數(shù)據(jù)。

以上證指數(shù)為例，圖2給出了2013/1/11—2014/7/15的上證指數(shù)的對(duì)數(shù)收益率，并給出了在置信水平99%和95%下，GARCH模型下參數(shù)（SGT）和半?yún)?shù)法（GDP）估計(jì)出的每日動(dòng)態(tài)VaR值。

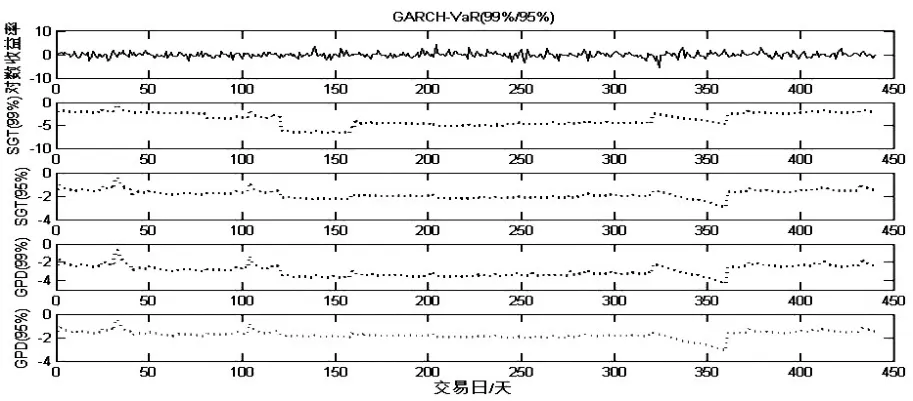
圖2 不同置信水平下GARCH模型的每日動(dòng)態(tài)VaR值

從圖2可以看出，在不同的置信水平下，基于GARCH模型下參數(shù)（SGT）和半?yún)?shù)法（GDP）估計(jì)出的VaR值都刻畫出了金融行業(yè)的市場(chǎng)風(fēng)險(xiǎn)，隨當(dāng)前波動(dòng)性產(chǎn)生了很明顯的變化。

3.4 模型的檢驗(yàn)和準(zhǔn)確程度的度量

在不同的置信水平下,采用LR、LRuc和DQ三種檢驗(yàn)方法綜合判斷各個(gè)動(dòng)態(tài)VaR模型的準(zhǔn)確性是否達(dá)到既定的水平，并根據(jù)式(19)求得各個(gè)模型的最大損失函數(shù)值lf,評(píng)估出這些動(dòng)態(tài)VaR模型準(zhǔn)確程度的優(yōu)劣。

在不同置信水平下，12種模型對(duì)于道瓊斯指數(shù)和上證指數(shù)的檢驗(yàn)結(jié)果在表2至表4中，各表中第一列是波動(dòng)率模型，第二列是標(biāo)準(zhǔn)化收益的分布，Lruc表示對(duì)應(yīng)模型給定樣本的Lruc檢驗(yàn)值，Lrind表示對(duì)應(yīng)模型給定樣本的Lrind檢驗(yàn)值，DQ表示對(duì)應(yīng)模型給定樣本的DQ檢驗(yàn)值，lf表示給定樣本各個(gè)模型的最大損失函數(shù)值，排序指的是最大損失函數(shù)值對(duì)應(yīng)的排列順序，沒有全部通過三種檢驗(yàn)的模型不參與排序。

表2給出了置信水平99.5%下的動(dòng)態(tài)VaR模型檢驗(yàn)。當(dāng)伴隨概率α=0.5%時(shí)，Lruc檢驗(yàn)、Lrind檢驗(yàn)和DQ檢驗(yàn)對(duì)應(yīng)的拒絕零假設(shè)的邊界值分別為

表2 置信水平99.5%下的動(dòng)態(tài)VaR模型檢驗(yàn)

由表2可知，在置信水平為99.5%下，12種模型均通過第一階段的三種檢驗(yàn)，即12種模型預(yù)測(cè)的準(zhǔn)確性都可以接受。由損失函數(shù)lf的估計(jì)值可知：在相同分布下，預(yù)測(cè)效果的優(yōu)劣順序是基于EGARCH、PGARCH、GARCH下的動(dòng)態(tài)VaR模型；在每類波動(dòng)率模型中，F(xiàn)SH-VaR、GPD-VaR模型優(yōu)于SGT-VaR、GED-VaR模型；12種動(dòng)態(tài)VaR模型中預(yù)測(cè)效果最差的是GARCH-GED模型。

表3給出了置信水平為97.5%下的動(dòng)態(tài)VaR模型檢驗(yàn)。當(dāng)伴隨概率α=2.5%時(shí)，Lruc檢驗(yàn)、Lrind檢驗(yàn)和DQ檢驗(yàn)對(duì)應(yīng)的拒絕零假設(shè)的邊界值分別為

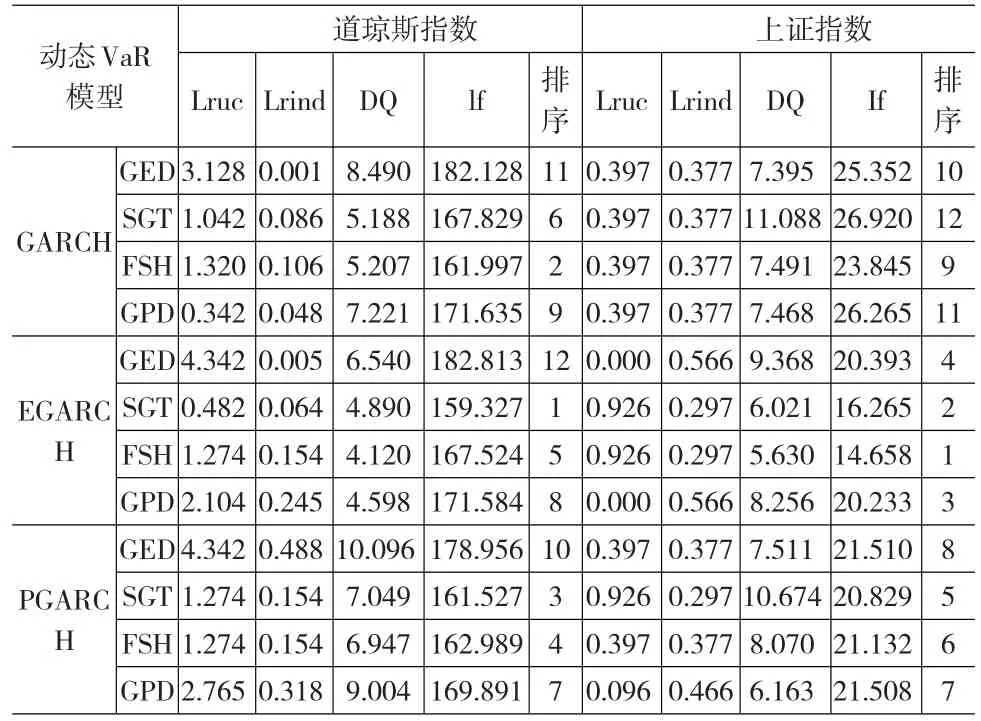
表3 置信水平97.5%下的動(dòng)態(tài)VaR模型檢驗(yàn)

由表3可知，在置信水平為97.5%時(shí)，12種模型都通過了準(zhǔn)確性檢驗(yàn)，具有可行性。根據(jù)損失函數(shù)lf的值可以看出，在相同分布下，動(dòng)態(tài)VaR模型中風(fēng)險(xiǎn)度量的準(zhǔn)確程度最差的是基于GARCH下的動(dòng)態(tài)VaR模型；在EGARCH和PGARCH模型中，SGT-VaR更能準(zhǔn)確的描繪市場(chǎng)，優(yōu)于半?yún)?shù)法的FSH-VaR、GPD-VaR模型，但并不顯著，預(yù)測(cè)能力最差的仍是GED-VaR模型。

表4給出了置信水平為95%下的動(dòng)態(tài)VaR模型檢驗(yàn)，當(dāng)伴隨概率α=5%時(shí)，Lruc檢驗(yàn)、Lrind檢驗(yàn)和DQ檢驗(yàn)對(duì)應(yīng)的拒絕零假設(shè)的邊界值分別為

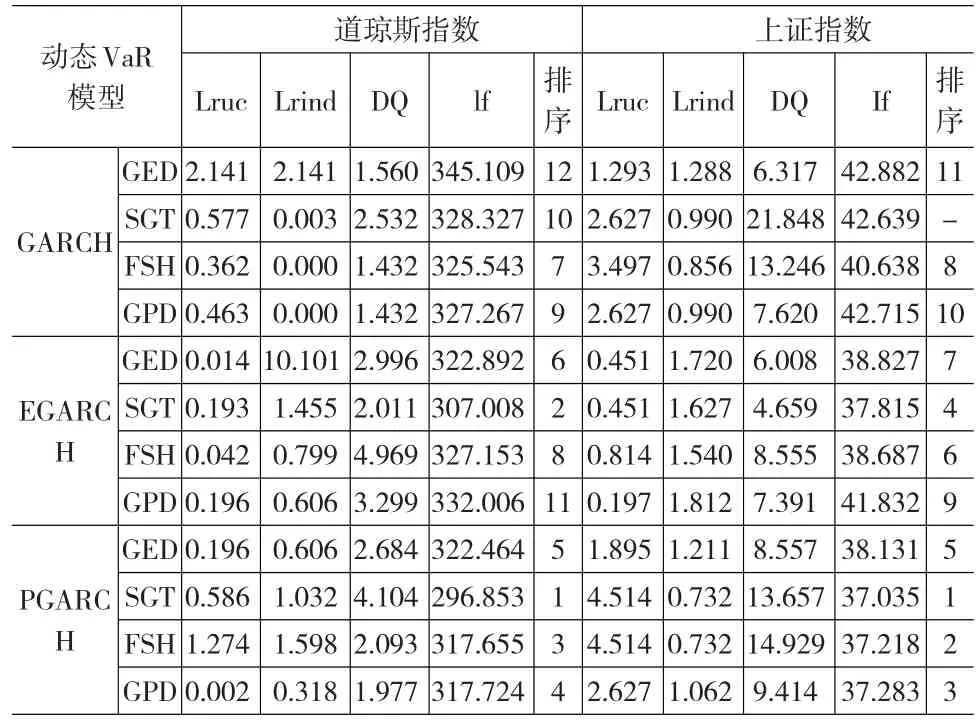
表4 置信水平95%下的樣本外動(dòng)態(tài)VaR模型檢驗(yàn)

由表4可知，在置信水平為95%下，對(duì)于道瓊斯指數(shù)，組合的12種模型都通過了第一階段準(zhǔn)確性檢驗(yàn)，模型具有可行性；對(duì)于上證指數(shù)，GARCH-SGT-VaR沒有通過檢驗(yàn)。根據(jù)損失函數(shù)lf的值，在相同分布下，不同GARCH模型的動(dòng)態(tài)VaR模型優(yōu)劣順序是基于PGARCH、EGARCH、GARCH下的動(dòng)態(tài)VaR模型；對(duì)于EGARCH和PGARCH模型而言，預(yù)測(cè)準(zhǔn)確程度最差的GED-VaR模型，參數(shù)法的SGT-VaR模型優(yōu)于半?yún)?shù)法的FSH-VaR、GPD-VaR模型；12種模型中風(fēng)險(xiǎn)度量準(zhǔn)確程度最高的模型是PGARCH-SGT-VaR模型，最差的是GARCH-GED-VaR模型。

4 結(jié)論

本文對(duì)GARCH族模型中三個(gè)經(jīng)典的模型：GARCH模型、EGARCH模型和PGARCH模型的風(fēng)險(xiǎn)收益率取了三種不同分布，并運(yùn)用了FSH方法組合了12種動(dòng)態(tài)VaR模型，并采用道瓊斯股票指數(shù)和上證指數(shù)檢驗(yàn)了12種模型在不同置信水平下的準(zhǔn)確性和風(fēng)險(xiǎn)度量能力的優(yōu)劣，由實(shí)證分析得出以下結(jié)論：

第一，道瓊斯股票市場(chǎng)和上證股票市場(chǎng)的收益率序列都具有尖峰厚尾的特點(diǎn)，不服從一般的正態(tài)分布。因此，在實(shí)際操作中，以正態(tài)分布計(jì)算VaR值的機(jī)構(gòu)或個(gè)人需提高風(fēng)險(xiǎn)意識(shí)，增強(qiáng)抵抗風(fēng)險(xiǎn)的能力。

第二，在相同分布假設(shè)下，GARCH模型的風(fēng)險(xiǎn)度量能力最弱，EGARCH模型和PGARCH模型能更好地刻畫市場(chǎng)的波動(dòng)情況。但在不同的置信水平下，EGARCH模型和PGARCH模型的度量能力也有差異，在置信水平為99.5%時(shí)，EGARCH模型的風(fēng)險(xiǎn)度量能力最好，在置信水平為95%，PGARCH模型的風(fēng)險(xiǎn)度量能力最好。

第三，對(duì)于GARCH模型、EGARCH模型和PGARCH模型，在采用參數(shù)法和非參數(shù)法分別對(duì)市場(chǎng)風(fēng)險(xiǎn)進(jìn)行估計(jì)時(shí)，假定市場(chǎng)收益率服從GED分布的模型市場(chǎng)風(fēng)險(xiǎn)度量能力最弱，這表明在這些方法中GED分布不能準(zhǔn)確的描述市場(chǎng)，SGT-VaR、FSH-VaR和GPD-VaR能更好地?cái)M合市場(chǎng)。在置信水平99.5%下，半?yún)?shù)模型（FSH-VaR，GPD-VaR）比參數(shù)模型（SGT-VaR）風(fēng)險(xiǎn)度量能力好；在置信水平97.5%下，參數(shù)模型（SGT-VaR）比半?yún)?shù)模型（FSH-VaR，GPD-VaR）風(fēng)險(xiǎn)度量能力略好，但并不顯著；在置信水平95%下，參數(shù)模型（SGT-VaR）風(fēng)險(xiǎn)度量能力優(yōu)于半?yún)?shù)模型（FSH-VaR，GPD-VaR）。可見，在參數(shù)模型和非參數(shù)模型都能較好的擬合市場(chǎng)時(shí)，置信水平越高，半?yún)?shù)模型（FSH-VaR，GPD-VaR）的風(fēng)險(xiǎn)度量能力越強(qiáng)，置信水平較低時(shí)，參數(shù)模型（SGT-VaR）的風(fēng)險(xiǎn)度量的準(zhǔn)確程度優(yōu)于半?yún)?shù)模型。

[1]Bali T,Theodossiou P.A Conditional-SGT-VaR Approach With Al?ternative GARCH Models[J].Annals of Research,2007,（151）.

[2]Balkema A,de Haan L.Residual Life at Great Age[J].Annals of Prob?ability,1974,(2).

[3]Barone Adesi G,Giannopoulos K,Vosper L.VaR Without Correla?tions for Nonlinear Portfolios[J].Journal of Futures Markets,1999, (19).

[4]Bekiros S,Georgoutsos D.Estimation of Value at Risk by Extreme Value and Conventional Methods:A Comparative Evaluation of Their Predictive Per-Formance[J].Journal of International Financial Mar?kets,Institutions&Money,2005,15(3).

[5]Chen Q,Chen R.Method of Value-at-Risk and Empirical Research for Shanghai Stock Market[J].Procedia Computer Science,2013,(17).

[6]Cheng W,Hung J.Skewness and Leptokurtosis in GARCH-typed VaR Estimation of Petroleum and Metal Asset Returns[J].Journal of Empirical Finance,2011,(18).

[7]Christoffersen P.Evaluating Interval Forecasting[J].International Eco? nomic Review,1998,(38).

[8]Engle R F,Manganelli S.CAViaR:Conditional Autoregressive Value at Risk by Regression Quantiles[J].Journal of Business and Economic Statistics,2004,(22).

[9]Fisher R,Tippett L.Limiting Forms of the Frequency Distribution of The Largest or Smallest Member of a Sample[J].Proceedings of the Cambridge Philosophical Society,1928,(24).

[10]Kupiec P.Techniques for Verifying the Accuracy of Risk Measure?ment Models[J].Journal of Derivatives,1995,(2).

[11]Marimoutou V,Raggad B,Trabelsi A.Extreme Value Theory and Val?ue at Risk:Application to Oil Market[J].Energy Economics,2009, (31).

[12]McNeil A,Frey R.Estimation of Tail-Related Risk Measures for Heteroscedasticity Financial Time Series:An Extreme Value Ap?proach[J].Journal of Empirical Finance,2000,(7).

[13]Polanski A,Stoja E.Incorporating Higher Moments Into Val?ue-at-risk Forecasting[J].Journal of Forecasting,2010,(29).

[14]Trenca I.The Use in Banks of VaR Method in Market Risk Manage?ment[J]Economic Sciences Series 2009.

[15]Zikovic S,Aktan B.Global Financial Crisis and Var Performance in Emerging Markets:A Case of EU Candidate States-Turkey and Croatia[J].Journal of Economics and Business,2009,（27）.

[16]高瑩,周鑫,金秀.GARCH模型在動(dòng)態(tài)VaR中的應(yīng)用[J].東北大學(xué)學(xué)報(bào)(自然科學(xué)報(bào)),2008,29(4).

[17]徐煒,黃炎龍.GARCH模型和VaR的度量研究[J].數(shù)量經(jīng)濟(jì)技術(shù)經(jīng)濟(jì)研究,2008,（1）.

[18]朱慧明等.基于序數(shù)空間的行業(yè)間戰(zhàn)略相對(duì)風(fēng)險(xiǎn)度量[J].統(tǒng)計(jì)與決策，2012,（13）.

（責(zé)任編輯/易永生）

F830

A

1002-6487（2016）23-0015-06

全國統(tǒng)計(jì)科學(xué)研究重點(diǎn)項(xiàng)目（2015LZ54）；安徽省高校自然科學(xué)重點(diǎn)基金項(xiàng)目（KJ2016A278）；安徽省軟科學(xué)項(xiàng)目（1502052039）；安徽師范大學(xué)哲學(xué)社會(huì)科學(xué)繁榮發(fā)展計(jì)劃首批重大項(xiàng)目（FRZD201302）；2014年安徽師范大學(xué)特色優(yōu)勢(shì)研究領(lǐng)域建設(shè)項(xiàng)目

張 瓊（1976—），女，安徽樅陽人，博士，副教授，研究方向：經(jīng)濟(jì)統(tǒng)計(jì)。