基于PM2.5指標的中國環境庫茲涅茨曲線估計

李龔

（上海交通大學 安泰經濟與管理學院，上海 200030）

基于PM2.5指標的中國環境庫茲涅茨曲線估計

李龔

（上海交通大學 安泰經濟與管理學院，上海 200030）

文章利用2014年中國138個城市截面數據與空間計量經濟學模型，基于擴展的傳統環境庫茲涅茨曲(EKC)，以PM2.5為環境指標，分析我國城市環境污染的空間相關性、EKC的形狀及其影響因素。結果發現：我國城市環境污染存在明顯的空間正相關性，截面數據模擬出的EKC曲線呈現“倒U形”，EKC假說在我國城市尺度得到證實；第二產業比重、人口密度、汽車保有量等與環境污染呈現正相關；城市產業結構升級，統籌區域發展，控制城市汽車保有量以及多城市聯合治理，有利于環境質量的提高。

環境庫茲涅茨曲線；PM2.5；空間計量經濟學模型；產業結構

0 引言

20世紀90年代初期，美國經濟學家Grossman和Krueger提出環境庫茲涅茨曲線(Environmental Kuznets Curve,EKC)，表明經濟增長與環境污染之間呈現“倒U形”關系，即環境質量會隨著經濟的增長呈現先惡化后改善的趨勢[1]。我國關于EKC的研究始于1999年，主要研究則在2002年以后。隨著經濟的不斷發展，社會對環境的關注日益增加，以及最近幾年“低碳經濟”的概念日益深入人心，環境問題也隨之成為經濟學研究的熱點。李慧明等(2003)研究發現，我國目前的環境質量仍然處在“局部改善，整體惡化”的狀態，并且還沒有達到EKC的轉折點，更加不可能達到EKC曲線的右側[2]。林伯強等（2009）以二氧化碳的排放量作為環境的代理指標，選取了1960年至2007年的中國二氧化碳排放量數據，使用了人均收入作為解釋變量的二次方程，估算出了我國EKC呈現“倒U形”關系，并且從理論上估計了我國EKC曲線的拐點是人均GDP37170元[3]。楊萬平等（2009）以1982年至2006年我國6大類工業環境污染數據為基礎，使用改進的熵值法估算我國的EKC曲線，其結果表明：我國經濟增長和環境污染之間不存在“倒U形”關系，而是呈現“正U形”關系[4]。蘇梽芳等(2009)利用中國28個省域2003年至2005年的面板數據，使用空間面板數據模型對EKC進行了估計，其結果表明：區域污染存在空間相關性，區域污染排放不僅受本區域人均收入影響，且相鄰區域的污染物排放也對本區域有重大影響，污染物排放具有空間溢出作用[5]。羅嵐等（2012）利用了2000年至2009年我國各省份的面板數據，以廢水、廢氣和固體廢棄物為環境指標，估算了各個指標下的EKC，其結果表明：以三廢作為環境指標估算出的EKC在大部分省均呈現“倒U形”；廢水污染在未來十年內可以實現與經濟發展同時改善，而固體廢棄物和廢氣則要相對較遲[6]。高宏霞等（2012）搜集了2000年至2009年31個省市自治區的面板數據，對全國31個省市自治區進行了研究，結果表明我國各省份的EKC呈現“倒U形”，并且大部分省份的EKC拐點是在2020年以后[7]。吳玉鳴等（2012）擴展了傳統的EKC模型，引入了城市化率，引進了人口數、人力資本、產業結構及對外開放等因素，利用2008年我國31個省份的截面數據，使用空間計量經濟學模型，分析了我國EKC的形狀及其影響因素，以及省域環境污染的空間相關性，其結果表明：我國省域環境污染之間存在明顯的空間自相關性；同時，30個省域的EKC呈現倒U型[8]。

本文所選取的環境指標是PM2.5濃度。PM2.5指的是大氣中粒子直徑小于或等于2.5微米的顆粒物，又稱細顆粒物。PM2.5有直徑小、表面積大、活性強、容易攜帶有毒有害物質、在大氣中停留時間長、輸送距離遠等特點，對人體健康影響較大。PM2.5的來源分為兩種，分別是自然源與人為源，其中主要來自人為源，包括道路揚塵、工業粉塵、化石燃料的燃燒等[9]。PM2.5的上述特征表明，PM2.5不是單一的污染物，而是一種綜合性環境污染指標。

綜上可知，學者們在研究EKC曲線的時候，大多只用人均GDP或人均收入這一個指標作為解釋變量，而忽略了其他指標的影響，比如產業結構、人口密度等，同時也忽略了區域環境污染之間的空間自相關性。選取的環境指標通常都是“三廢”、粉塵、二氧化硫、二氧化碳等，這些都是單一的環境指標而不是綜合的環境指標。文獻中得到的EKC形狀各異，有“倒U形”[10]、“正U形”[4,12]、“N形”[11]、“N形+倒U形”[13]、“凹形”[14]等。

與以往EKC的研究相比，本文有如下的三點不同：第一，本文利用了PM2.5濃度作為環境污染的指標。在國內的EKC研究中，尚且沒有選擇PM2.5濃度為環境指標；同時PM2.5本身是一種綜合的環境指標，與之前的EKC研究中使用的單一指標不同。第二，本文搜集了2014年我國138個城市的相關截面數據。目前，在相關EKC研究中，大多是基于國家或者省市自治區層面，很少有城市層面的EKC研究。第三，基于PM2.5易擴散的物理特征，本文采用了空間計量經濟學模型，從而控制相鄰地區PM2.5的相關性。

1 研究模型、方法和數據

1.1 空間自相關[15]

空間自相關指的是某個變量在同一分布區域里的觀察值之間存在潛在的相互依賴關系。全局區域自相關是從區域整體上刻畫空間聚集情況。通常用全局莫蘭指數(Moran’s I)來度量全局空間自相關，其計算公式如下：

在衡量某一特定區域附近的空間聚集情況的時候，通常選用局部莫蘭指數(Local Moran’s I)，其公式如下：

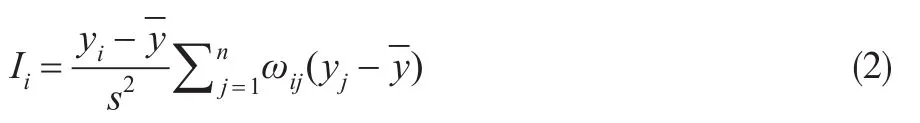
其中yi和yj分別是第i和第j個地區的觀察值，n是地區總數量，表示所選指標的均值，s2是所選指標的方差，ωij是空間權重的值。

全局莫蘭指數的取值范圍在-1到1之間，大于0則存在正相關關系，小于0則存在負相關關系，等于0則不存在空間關系，絕對值越大則表示相關關系越強。正的局部莫蘭指數表示該區域的高值被周圍的高值所包圍，或者該地區的低值被周圍的低值所包圍；反之則表示該區域的高值被周圍的低值所包圍，或該區域的低值被周圍的高值所包圍。

1.2 空間計量經濟學模型

空間計量經濟學模型可以分為空間滯后模型(Spatial Lag Model,SLM)和空間誤差模型(Spatial Error Model, SEM)。

(1)空間滯后模型(SLM)[16]

在模型中考慮因變量的空間滯后項，則可以選擇空間滯后模型：

其中，yi是因變量；ω是n×n階的空間權重矩陣；∑i≠jωijyi是所有鄰近區域地區因變量的加權和，作為因變量的空間滯后項，ρ是衡量因變量溢出效應的參數，稱為空間自回歸系數；xi是n×k的自變量矩陣，β是參數，反映自變量對因變量的影響程度；εi是隨機誤差項。

(2)空間誤差模型(SEM)[17]

當因變量的空間依賴性存在于隨機擾動項的時候，則可以考慮使用空間誤差模型：

其中，μi是隨機誤差項；λ是μi的自回歸系數，用來衡量鄰近地區因變量yi的誤差項加權總和∑i≠jωijμi對因變量yi誤差項的影響程度；εi是正太分布的隨機誤差項。

1.3 選取指標

本文所涉及的指標如下：

(1)PM2.5濃度：作為實證分析中環境質量的代理指標，它與環境質量呈現負相關關系，即環境質量得到改善則PM2.5濃度下降，反之PM2.5濃度上升。

(2)人均GDP：根據環境庫茨涅茲曲線的理論，經濟的發展與環境污染之間呈現“倒U形”關系，即在經濟發展初期，社會以犧牲環境質量為代價來換取人均GDP的提高，環境質量開始逐步惡化，然而，當人均GDP到達一定程度之后，社會開始逐步關注環境質量，于是伴隨著人均GDP的逐步提高，環境質量也在不斷提高。

(3)汽車保有量：汽車尾氣是PM2.5的主要來源之一。本文為了研究PM2.5濃度與人均GDP的關系，需要控制住其他影響PM2.5濃度的變量，而城市的汽車保有量是一個影響PM2.5濃度的重要因素。本文假設城市的汽車保有量與城市的PM2.5呈現正相關關系，即城市的汽車保有量增加會導致PM2.5的濃度也相應地增加。

(4)總降水量：雨水會溶解大氣中的有害顆粒物，從而達到清潔大氣的作用。本文假設PM2.5濃度與降水量呈現負相關關系，即降水量越大則對應的PM2.5濃度就會越低，反之，PM2.5濃度將會越高。

(5)第二產業比重：在第一、第二和第三產業中，第一和第三兩個產業是相對比較清潔的，不會對環境造成過多的影響，而第二產業則是影響環境質量的重要來源。本文假設第二產業的比重與PM2.5濃度呈現正相關關系，即第二產業的比重越大，則PM2.5濃度就會越高，反之PM2.5濃度就會越低。

(6)人口密度：人口密度越高則對環境的壓力就會越大，造成的環境污染就可能更加嚴重。本文假設人口密度與PM2.5之間呈現正相關關系，即人口密度越高，對應的PM2.5濃度就會越高，反之PM2.5濃度就會越低。

(7)是否在秦嶺淮河以北：這個指標作了啞變量處理，處于秦嶺淮河以北的城市取1，否則取0。秦嶺淮河線從地理上將我國分成了南北雙方，同時也是人文上的分割線，是我國所特有的。我國800毫米等降水線于秦嶺淮河一線重合，越向北降水量越少；我國在秋冬兩季實行集體供暖，而供暖城市絕大多數都是位于秦嶺淮河以北，供暖會消耗大量能源，同時會產生大量的環境污染。本文假設該啞變量與PM2.5濃度呈現正相關關系，即在同等情況下，秦嶺淮河以北的PM2.5濃度會高于秦嶺淮河以南。

1.4 數據說明與實證模型構建

本文所涉及到的數據源于我國2014年138個城市，包括：PM2.5濃度(PM25，單位：微克/立方米)、降水量(RAIN-FALL，單位：毫米)、汽車保有量(CARNUM，單位：萬輛)、人均GDP(單位：元)、第二產業比重(INDUSTRY)、人口密度(POPDENSITY，單位：萬人/平方公里)以及是否秦嶺淮河以北(ISNORTH)。其中，2014年138個城市的PM2.5濃度數據和降水量數據來自于新浪網；汽車保有量、人均GDP和第二產業比重來自于2014年各城市國民經濟與社會發展統計公告；人口密度是根據各個城市人口數量和面積計算得到。

本文是以PM2.5濃度作為環境指標，控制影響PM2.5濃度的其他的變量，即汽車保有量、總降水量、第二產業比重、人口密度、是否秦嶺淮河以北，來估計人均GDP與環境質量的關系，從而得出環境庫茨涅茨曲線的形狀。本文選用的是基于截面數據建立的靜態空間計量模型，將PM25、AVGGDP、CARNUM、RAINFALL和POPDENSITY這幾個變量進行對數化處理，根據模型(3)和模型(4)分別建立如下的兩個空間計量模型，即空間滯后模型(SLM)和空間誤差模型(SEM)：

空間滯后模型(SLM)：

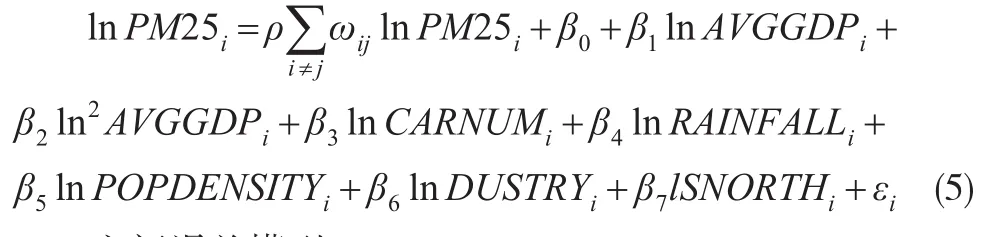
空間誤差模型(SEM)：

2 實證結果分析

2.1 空間相關性的檢驗

首先，基于城市空間實際距離生成空間權重矩陣，然后對138個城市的對應變量數據進行全局空間自相關檢驗，其結果表1所示，其中I表示全局莫蘭指數，E(I)表示其理論期望，SD(I)表示其理論標準差，Z表示其標準化值。

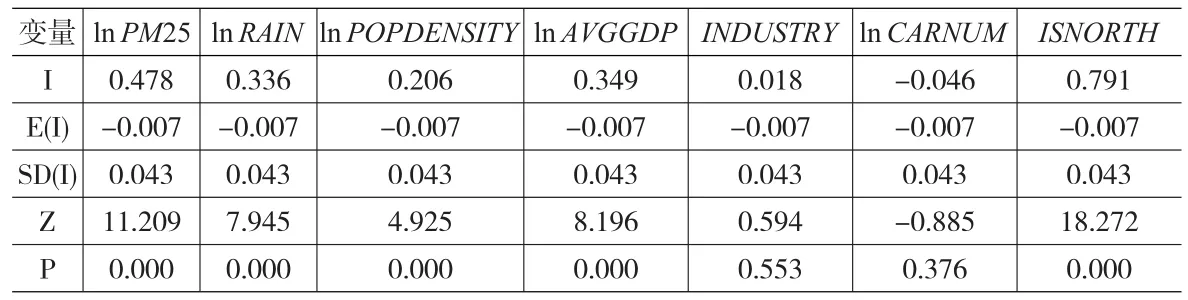
表1 EKC變量的全局空間自相關檢驗

根據距離空間權重計算PM2.5，降水量、人口密度、人均GDP以及是否是秦嶺淮河以北的全局莫蘭指數分別是0.478，0.336，0.206，0.349，0.791，都通過了1%的顯著性檢驗水平，說明這些變量在空間分布上都存在明顯的正自相關。而第二產業比重與汽車保有量相對而言就不存在明顯的空間自相關性。綜合以上結果，在研究城市EKC問題的時候不能忽視城市之間的空間效應。

2.2 空間計量估計與分析

為了與城市截面的EKC空間計量結果進行比較，本文首先用常規的普通最小二乘法(OLS)進行回歸估計，然后使用Stata進行SLM和SEM兩個模型的估計，并得到結果，見表2。

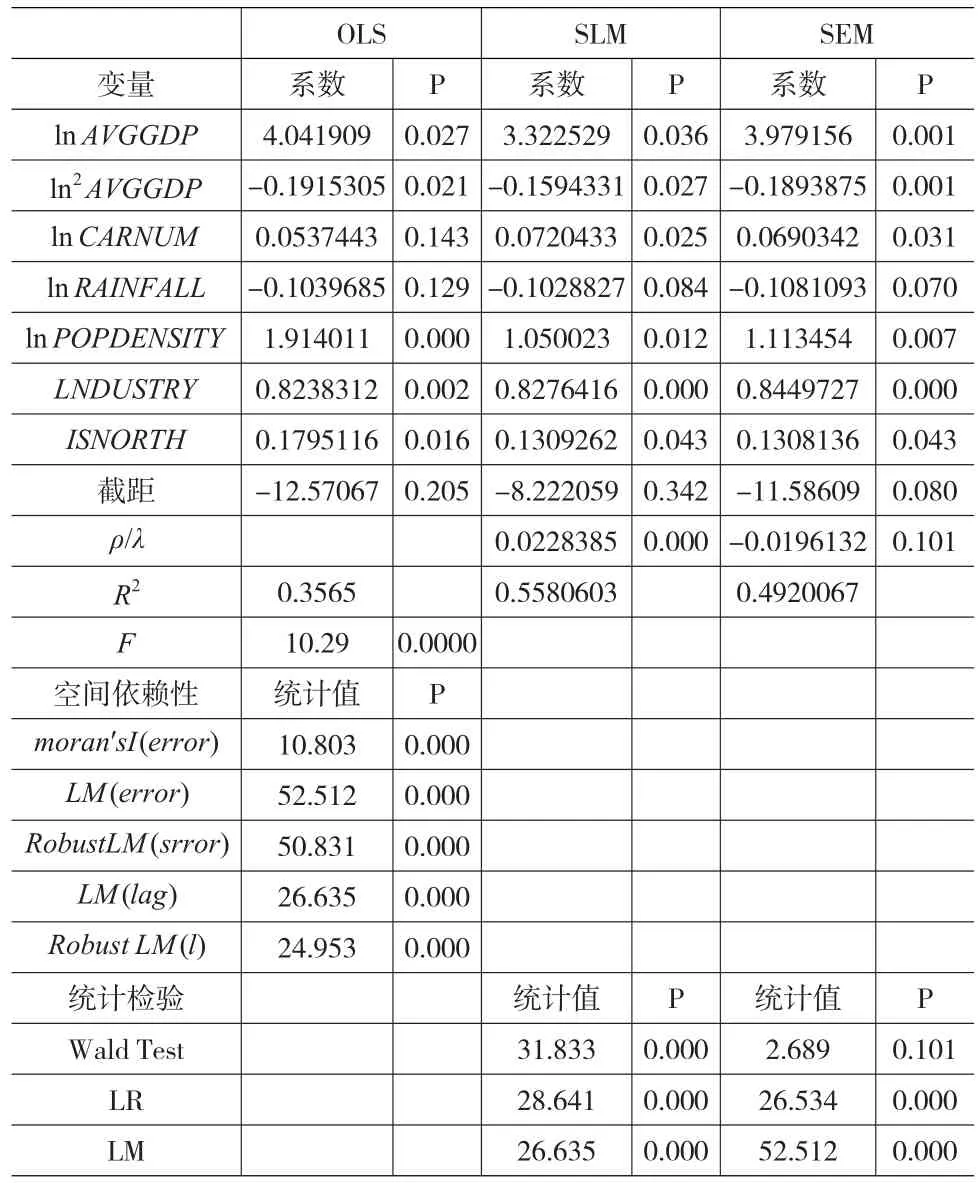
表2 OLS、SLM和SEM估計結果

OLS的估計結果表明：OLS的擬合優度是0.3569，F值是10.29，模型整體上通過了1%顯著性檢驗。人均GDP、人均GDP的平方、是否秦嶺淮河以北，通過了5%的顯著性檢驗；人口密度和第二產業比重通過了1%的顯著性檢驗；而汽車保有量和降水量則沒有通過12%的顯著性檢驗，即不顯著。前面的全局莫蘭指數檢驗表明城市之間的因變量存在明顯的空間相關性，OLS的結果與之不符，表明OLS模型的設定存在問題，即OLS可能忽略了城市之間的空間相關性。

從SLM和SEM的估計結果可以看出：SLM中人均GDP、人均GDP的平方、汽車保有量、人口密度、第二產業比重以及是否秦嶺淮河以北，這幾個變量都通過了5%的顯著性檢驗；而降水量通過了10%的顯著性檢驗；空間自相關系數通過Wald Test、LRTest以及LM Test，顯著性都在1%。SEM中人均GDP、人均GDP的平方、汽車保有量、人口密度、第二產業比重以及是否秦嶺淮河以北，這幾個變量也都通過了5%的顯著性水平檢驗；而降水量通過了10%的顯著性檢驗；空間自相關系數通過LRTest和LM Test的檢驗，顯著性在1%，而在Wald Test中，沒有通過10%的顯著性檢驗；SLM和SEM的擬合優度R2分別是0.5580603和0.4920067，明顯大于OLS的0.3569。

根據模型的估計結果，得出SLM的方程，即EKC模型是：

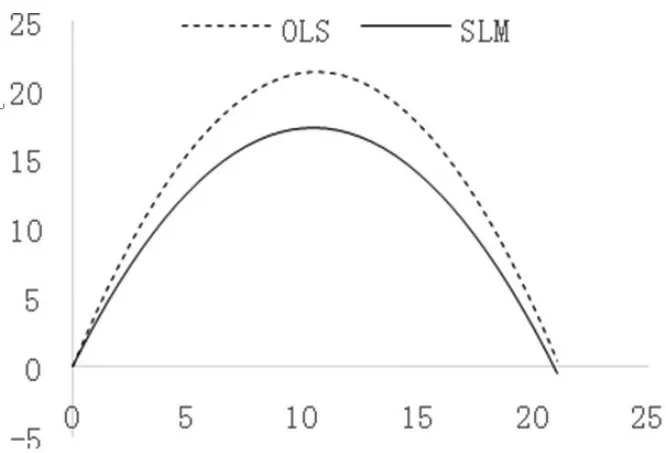
圖12014 年中國138個城市截面

對于人均GDP而言，OLS和SLM模型的走勢如圖1。可以看出，OLC和SLM估算出的EKC都呈現“倒U形”，且兩條曲線的拐點相近。同時在SLM估算出的ELC中，當lnAVGGDP達到10.4198219的時候達到拐點，即人均GDP達到33517.5元時，EKC達到拐點。根據數據可以知道，我國138個城市中絕大部分城市的人均GDP都超過了上述拐點，只有29個城市沒有超過拐點。即這些城市目前仍是以犧牲環境質量為代價來發展經濟。從圖上看，SLM的曲線比數據EKC圖OLS的曲線平緩，因為OLS沒有考慮到空間的自相關效應，把周邊地區溢出的污染也算進本地區的污染中，使得PM2.5濃度對人均GDP的變化更加敏感，說明了在忽略空間自相關效應的OLS中，夸大了人均GDP對PM2.5濃度的影響，從而可能會導致在環境治理上過度關注人均GDP的變化而忽略其他因素。

2.3 SLM的結果分析

汽車保有量（lnCARNUM）對環境污染的回歸系數是0.0720433，通過5%的顯著性水平檢驗，表明在不考慮其他因素的情況下，汽車保有量每增加1%，環境損失將增加0.0720433%。較大規模的汽車保有量對環境保護造成了較大的壓力。一線大中型城市目前已經對城市的汽車數量進行一定的限制，這些措施也進一步表明了較大的汽車保有量對環境質量確實造成了不小的壓力。

人口密度（lnPOPDENSITY）對環境污染的回歸系數是1.050023，通過了5%的顯著性水平檢驗，表明人口密度每增加1%，環境損失將增加1.050023%。京津冀的環境污染相對比較嚴重，這與當地較高的人口密度也不無關系。這就表明了要改善大中型城市的環境就有必要合理化分配城市配套資源，減小區域發展之間的不平衡。

降水量（lnRAINFALL）和是否秦嶺淮河以北（ISNORTH）這兩個因素對環境污染的回歸系數分別是-0.1028827和0.1309262，分別通過了10%和5%的顯著性檢驗。降水量反映了各個城市之間的氣候差異。降水較多的南方會沖洗掉環境中的一些雜質，這樣有利于環境的自我凈化和修復，即在其他因素不變的情況下，降水量越多，環境質量越好。這與模型回歸的結果是相同的。是否處與秦嶺淮河以北從地理的角度講我國分成了南方和北方。北方城市在冬季會采取集中供暖，而南方城市則沒有。北方城市冬季采取集中供暖必然會給環境造成損失，這與模型的回歸結果也是一致的。

第二產業比重（INDUSTRY）對環境的回歸系數是0.8276416，通過了1%的顯著性水平檢驗，表明了第二產業比重每增加1%，環境損失就會增加0.8276416%。第二產業主要以制造業為主，需要消耗大量的自然資源，同時也會對環境造成不可避免的傷害。模型的系數中第二產業比重的回歸系數是最大的，說明了在模型列舉的因素中，第二產業比重是對環境影響最大的。這進一步表明了產業結構調整對環境保護的重要性。

與SLM估計結果比較，OLS中人口密度、是否秦嶺淮河以北這兩個變量的系數偏大，原因是OLS模型中把其他周邊區域的影響也算成本地區的影響，故而OLS的結果會偏大；第二產業比重、降水量的系數與OLS模型的結果相比，幾乎沒有變化；OLS模型中汽車保有量的系數比SLM中的系數偏小，說明汽車保有量的影響在OLS中被低估了，同時在OLS中該變量沒有通過顯著性檢驗，即OLS不能有效說明汽車保有量的影響。

3 結論

本文擴展了傳統的環境庫茨涅茨曲線模型，添加了汽車保有量、人口密度、降水量、第二產業比重、是否秦嶺淮河以北這5個變量，利用空間計量經濟學模型，研究了我國138個城市的EKC的形狀及其影響因素。結果發現：我國PM2.5濃度在空間分布上存在明顯的正自相關關系，說明我國各個城市環境污染不是相互獨立的，而是存在空間正向自相關的；利用2014年度我國138個城市的相關截面數據模擬得出的EKC圖形是呈現“倒U形”，表明EKC假說在我國可以得到歷史數據的支持；同時估計出擴展后的EKC對人均GDP的拐點是33517.5元，即在其他因素不變的情況下，人均GDP達到或超過33517.5元的城市的環境質量會隨著經濟的發展而逐步改善。

基于上述的結果獲得的政策建議如下：由于環境污染是存在空間相關性的，所以城市在治理環境的時候，要注重城市區域之間的合作；城市的產業結構要不斷調整，要逐步改善第一、第二和第三產業的比重，積極發展第三產業，使產業逐步升級；大中型城市要合理控制汽車保有量，提升城市交通和環境質量；在推進城市化的過程中，要逐步實現城市之間基礎設施及相關服務的均衡，避免人口過度集中。

[1]Grossman G M,Krueger A B.Economic Growth and The Environment [J].Quarterly Journal of Economics,1995,110(2).

[2]李慧明,卜欣欣.環境與經濟如何雙贏——環境庫茲涅茨曲線引發的思考[J].南開學報（哲學社會科學版）,2003，(1).

[3]林伯強,蔣竺均.中國二氧化碳的環境庫茲涅茨曲線預測及影響因素分析[J].管理世界,2009，(4).

[4]楊萬平,袁曉玲.環境庫茲涅茨曲線假說在中國的經驗研究[J].長江流域資源與環境,2009,18(8).

[5]蘇梽芳,胡日東,林三強.環境質量與經濟增長庫茲尼茨關系空間計量分析[J].地理研究,2009，(2).

[6]羅嵐,鄧玲.我國各省環境庫茲涅茨曲線地區分布研究[J].統計與決策,2012，(10).

[7]高宏霞,楊林,付海東.中國各省經濟增長與環境污染關系的研究與預測——基于環境庫茲涅茨曲線的實證分析[J].經濟學動態, 2012，(1).

[8]吳玉鳴,田斌.省域環境庫茲涅茨曲線的擴展及其決定因素[J].地理研究,2012,31(4).

[9]王瑋,湯大鋼,劉紅杰.中國PM2.5污染狀況和污染特征的研究[J].環境科學研究,2000,13(1).

[10]高靜.中國SO2與CO2排放路徑與環境治理研究:基于30個省市環境庫茲涅茨曲線面板數據分析[J].現代財經,2012，(8).

[11]丁繼紅,年艷.經濟增長與環境污染關系剖析:以江蘇省為例[J].南開經濟研究,2010,(2).

[12]李憶雯,王君,周麗蓉.四川經濟增長與環境污染關系的實證研究[J].統計與決策,2012，(13).

[13]蘇營營,余建林,蒲鳳蓮等.嘉興市環境庫茲涅茨曲線特征分析[J].環境科學與管理,2012,37(2).

[14]班春峰,徐夢潔,趙紫玉等.河南省環境庫茲涅茨曲線的實證研究[J].環境科學與管理,2008,33(9).

[15]Anselin L.Local Indicators of Spatial Autocorelation—LISA[J].Geo?graphical Analysis,1995,27(2).

[16]Ord K.Estimation Methods For Models of Spatial Interaction[J].Jour?nal of the American Statistical Association,1975,70(349).

[17]Anselin L.Spatial Econometrics:Methods and Models[J].Journal of the American Statistical Association,1990,85(411).

（責任編輯易永生）

X820

A

1002-6487（2016）23-0021-04

李 龔（1992—），男，江蘇鹽城人，碩士研究生，研究方向：產生經濟學。