應用Mathematica計算單擺任意擺角下的振動曲線
謝忠偉
摘 要:本文應用Mathematica軟件,繪制在無阻尼自由振動中,不同擺角下,單擺的振動曲線。通過對振動曲線的研究,給出了單擺的周期隨擺角不同而變化的定性規律,為高中物理教學提供了便捷的途徑。
關鍵詞:Mathematica;單擺;擺角;振動曲線
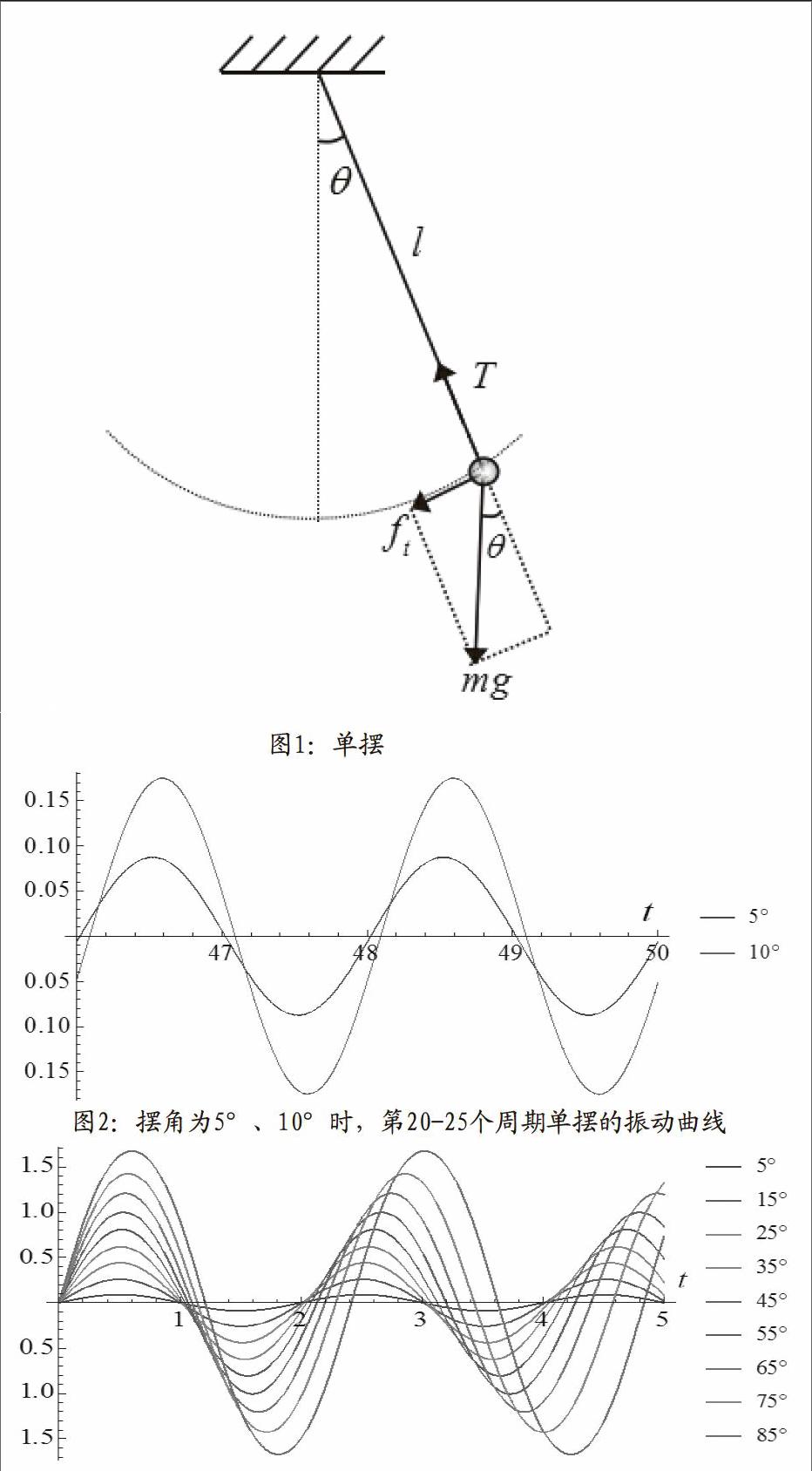
單擺是由一根質量可忽略且不可伸縮的細線,上端固定,下端系一可看作質點的重物所構成的裝置,如圖1所示。單擺在擺角小于5°時的無阻尼振動是高中物理中一個作為簡諧振動的典型實例。
現取逆時針為正方向,則任意時刻質點所受重力的分力為。當擺角很小時,,得,此即為單擺所受的線性恢復力[1]。此時,單擺運動為簡諧運動。
就高中階段物理而言,如何能夠給學生展現出任意擺角下,單擺的振動周期與擺角的關系,就是一個難題。
通過應用Mathematica軟件,可使這個復雜的問題,很直觀而準確地用圖像的方式呈現出來,便于學生理解。本文為了避免使用復雜的計算機語言而帶來操作上的困難,因此,基于Mathematica 9應用環境下,使用最簡單、最基本的函數語言進行計算實現的。
1.計算在小角度5°和10°時,單擺的振動曲線,如圖2所示。
擺角為10°和5°時,在短時間內,振動幾乎同步;而隨著周期的增加,使兩周期的差逐漸累加,便可明顯看出10°時的周期略大于5°,如圖2。利用Mathematica中“獲取坐標”的簡單操作,可直接讀出各點的坐標。依此,可粗略計算出擺角為10°時的周期為22.00381s;擺角為5°時的周期為2.00095s,而在的條件下,單擺簡諧運動的周期為2s。因此,若要求精度不高,可選擇擺角小于10°時作為簡諧運動進行研究。
2.計算無阻尼下單擺在擺角為5°、15°、25°、35°、45°、55°、65°、75°、85°運動曲線,如圖3所示。
由圖3可知,隨著擺角角度的增加,單擺的振動周期逐漸增加,且隨著擺角角度的變大,其周期增速變大。
3.結論。
基于Mathematica軟件,可研究任意擺角下,各種情況的振動,如:阻尼振動、受迫振動等。由此繪制的圖形,不但精度高且直觀,非常適合給高中學生進行定性地分析和講解。同時,還能有效地拓展學生思維,點燃學生學習的動力。
參考文獻:
[1]張三惠.大學基礎物理學(下)[M].北京:清華大學出版社,2007.
(作者單位:遼寧鞍山臺安縣第二高級中學物理組)

