基于沖突圖模型策略?xún)?yōu)先權(quán)排序法的強(qiáng)度偏好排序研究
侯宇航,徐海燕
(南京航空航天大學(xué)經(jīng)濟(jì)與管理學(xué)院,南京 211106)
?
基于沖突圖模型策略?xún)?yōu)先權(quán)排序法的強(qiáng)度偏好排序研究
侯宇航,徐海燕
(南京航空航天大學(xué)經(jīng)濟(jì)與管理學(xué)院,南京 211106)
沖突分析圖模型中強(qiáng)度偏好的引入增加了決策者的感情色彩,進(jìn)一步豐富了決策者的偏好信息。在強(qiáng)度偏好下運(yùn)用沖突分析圖模型理論對(duì)沖突進(jìn)行建模時(shí),有一個(gè)非常重要的問(wèn)題——強(qiáng)度偏好的排序。本研究首先將簡(jiǎn)單偏好下的策略?xún)?yōu)先權(quán)排序法擴(kuò)展到強(qiáng)度偏好;然后以“蘭州水污染事件”為例,在蘭州威立雅水務(wù)公司、地方政府和中石化蘭州分公司存在強(qiáng)度偏好的情況下,運(yùn)用擴(kuò)展后的策略?xún)?yōu)先權(quán)排序法求取各決策者的強(qiáng)度偏好序列,并對(duì)此次水污染事件引發(fā)的沖突進(jìn)行建模、分析,模擬了沖突事件中的談判和協(xié)商過(guò)程,求得沖突各方的均衡解,案例分析過(guò)程也從戰(zhàn)略層面為我國(guó)實(shí)現(xiàn)經(jīng)濟(jì)的可持續(xù)發(fā)展提供借鑒。
沖突分析圖模型;強(qiáng)度偏好;策略?xún)?yōu)先權(quán)排序法;“蘭州水污染事件”
1 引言
沖突分析圖模型法(GMCR)是在經(jīng)典對(duì)策論(Game Theory)[1]和偏對(duì)策理論(Metagame Theory)[2]的基礎(chǔ)上發(fā)展起來(lái)的一種對(duì)沖突行為進(jìn)行正規(guī)分析的決策分析方法,其借助于集合論和圖論,將沖突行為數(shù)學(xué)模型化,進(jìn)行沖突事態(tài)的過(guò)程分析與結(jié)果預(yù)測(cè),為決策者提供戰(zhàn)略建議。圖模型理論GMCR首先由Kilgour等[3]創(chuàng)建,F(xiàn)ang Liping教授等[4]對(duì)其進(jìn)行了完整的描述。目前,該方法已被應(yīng)用于非常廣泛的領(lǐng)域,包括環(huán)境沖突[5]、戰(zhàn)爭(zhēng)沖突[6]、貿(mào)易談判[7]、復(fù)雜產(chǎn)品過(guò)程沖突[8]等。
對(duì)于沖突問(wèn)題的研究,許多都是基于經(jīng)典博弈論展開(kāi)的。劉德海[9]建立了地方政府部門(mén)與社會(huì)弱勢(shì)群體之間的演化博弈模型,分析了地方政府部門(mén)機(jī)會(huì)主義行為導(dǎo)致的群體性突發(fā)事件呈現(xiàn)擴(kuò)大化的趨勢(shì)。陳珍等[10]將演化博弈理論引入到工資集體協(xié)商機(jī)制中來(lái),為緩解工資收入分配中企業(yè)與勞動(dòng)者之間的沖突提供新思路。浦徐進(jìn)等[11]借助演化博弈方法,構(gòu)建了企業(yè)與官員策略互動(dòng)的支付矩陣,為食品質(zhì)量安全問(wèn)題的解決提供決策建議。趙禮強(qiáng)等[12]從分析消費(fèi)者效用出發(fā),建立了雙渠道環(huán)境下需求依賴(lài)價(jià)格變化的需求函數(shù),運(yùn)用博弈論建立決策模型,對(duì)雙渠道供應(yīng)鏈的協(xié)調(diào)契約進(jìn)行設(shè)計(jì),從而實(shí)現(xiàn)供應(yīng)鏈雙渠道沖突的協(xié)調(diào)。博弈論是定量分析,需要精確的數(shù)據(jù),但在現(xiàn)實(shí)生活中,精確的數(shù)據(jù)信息是無(wú)法獲得的,此時(shí)基于定量研究的博弈模型就失去了它原有的效用。與博弈論相比,圖模型理論GMCR的使用更為方便、靈活,該方法只需決策者給出相對(duì)的偏好信息就能提供沖突問(wèn)題的均衡解決方案,從而為決策者提供一定的決策依據(jù)。
圖模型理論GMCR解決沖突事件主要有兩個(gè)基本步驟:建模和穩(wěn)定性分析。目前,對(duì)于建模過(guò)程的研究主要集中于偏好信息的表達(dá)與處理。在圖模型理論GMCR中,偏好是決策者根據(jù)自己的期望目標(biāo)以及自己對(duì)沖突的判斷所得出狀態(tài)之間的優(yōu)劣[3]。在最初的研究中,只考慮了簡(jiǎn)單偏好[1],包括兩種基本形式:“?”優(yōu)于和“~”等價(jià)于。而在現(xiàn)實(shí)的沖突中,隨著沖突事態(tài)的發(fā)展,決策者掌握信息的增多,以及決策者對(duì)沖突的感情色彩的變化,決策者在表達(dá)偏好信息時(shí),不僅僅存在一個(gè)狀態(tài)優(yōu)劣的比較,而且還存在一個(gè)偏好強(qiáng)弱的程度之分,基于此,學(xué)者Hamouda等[13-14]在簡(jiǎn)單偏好的基礎(chǔ)上,加上一個(gè)強(qiáng)度“>>”信息,于2004年給出了具有偏好強(qiáng)度的偏好結(jié)構(gòu),并將其加入到圖模型理論GMCR中。針對(duì)偏好排序的主觀性問(wèn)題,F(xiàn)ang Liping等[15]等針對(duì)簡(jiǎn)單偏好的情況,提出了策略加權(quán)平均法(Option Weighting)、策略?xún)?yōu)先權(quán)排序法(Option Prioritizing)和直接狀態(tài)排序法(Direct Ranking)三種方法。策略加權(quán)平均法不能將決策者的感情色彩生動(dòng)地展示出來(lái);直接狀態(tài)排序法必須對(duì)每個(gè)狀態(tài)的偏好進(jìn)行分析比較,當(dāng)處理復(fù)雜的沖突模型時(shí),該方法是很難實(shí)現(xiàn)的;策略?xún)?yōu)先權(quán)排序法避免了前兩種方法的缺點(diǎn),該方法既能展示出決策者的想法,又能應(yīng)用于復(fù)雜的沖突模型。
目前,對(duì)于強(qiáng)度偏好下沖突分析圖模型理論的研究成果已經(jīng)很多。學(xué)者Hamouda等[13]于2004年提出具有偏好強(qiáng)度的偏好結(jié)構(gòu)時(shí),探討了決策者為兩個(gè)情況下的均衡解;并根據(jù)對(duì)手反擊的程度,將穩(wěn)定性定義為標(biāo)準(zhǔn)情況的穩(wěn)定、強(qiáng)穩(wěn)定性和弱穩(wěn)定性。2006年又將決策者擴(kuò)展到為多個(gè)(N>2)的情況[14]。隨后,徐海燕教授根據(jù)強(qiáng)度偏好結(jié)構(gòu)的特點(diǎn),相繼提出三等級(jí)水平和多等級(jí)水平的偏好結(jié)構(gòu),并定義了相應(yīng)偏好結(jié)構(gòu)下的穩(wěn)定性[16-17]。韓雪山[18]在基于圖模型理論GMCR的框架下,定義了強(qiáng)度偏好下的結(jié)盟穩(wěn)定性。但這些研究主要集中于強(qiáng)度偏好下穩(wěn)定性的研究,而對(duì)強(qiáng)度偏好序列如何獲取的研究很少。現(xiàn)有獲取強(qiáng)度偏好序列的方法依然是直接狀態(tài)排序法,這種方法適合于比較簡(jiǎn)單的沖突模型,然而當(dāng)處理復(fù)雜的沖突模型時(shí),該方法是很難適用的,因此也就很難將現(xiàn)有的強(qiáng)度偏好圖模型沖突分析理論應(yīng)用到實(shí)際的沖突中。
本文考慮當(dāng)前圖模型理論GMCR框架下強(qiáng)度偏好排序方法研究的不足,立足于我國(guó)經(jīng)濟(jì)發(fā)展與環(huán)境保護(hù)的實(shí)際矛盾,將簡(jiǎn)單偏好下的策略?xún)?yōu)先權(quán)排序法擴(kuò)展到強(qiáng)度偏好,用以處理更為復(fù)雜的沖突模型中決策者強(qiáng)度偏好的排序問(wèn)題,并將擴(kuò)展后的方法應(yīng)用到“蘭州水污染事件”中,對(duì)沖突進(jìn)行建模、分析,在理論創(chuàng)新的同時(shí),擴(kuò)展其應(yīng)用領(lǐng)域,為我國(guó)從戰(zhàn)略層面破解環(huán)境資源沖突提供很好的借鑒思路。
2 基于強(qiáng)度偏好的沖突分析圖模型 理論
2.1 沖突分析的圖模型
沖突分析圖模型是一種對(duì)沖突進(jìn)行建模、分析和決策的方法,以V={N,S,P,G}來(lái)表示。其中N(N≥2)表示包含全部決策者的有限非空集合;S表示所有可行狀態(tài)的非空集合;P表示決策者的偏好信息;G表示決策者的狀態(tài)轉(zhuǎn)移圖。該方法用于解決沖突的過(guò)程包括:識(shí)別現(xiàn)實(shí)沖突中的決策者和策略,分析可行狀態(tài)和狀態(tài)轉(zhuǎn)移情況以及決策者的偏好信息,計(jì)算個(gè)體穩(wěn)定性和均衡解,解決沖突。
2.2 強(qiáng)度偏好
強(qiáng)度偏好下,將沖突分析圖模型中決策者i的偏好結(jié)構(gòu)表示為P={>>i, >i, ~i}。對(duì)于任意的兩個(gè)可行狀態(tài){s, q}滿(mǎn)足以下幾個(gè)性質(zhì):
性質(zhì)一:>>i, >i滿(mǎn)足不對(duì)稱(chēng)性。對(duì)于s, q∈S,s>>iq或s>iq與q>>is或q>is兩者不能同時(shí)成立;
性質(zhì)二:~i滿(mǎn)足自反性和對(duì)稱(chēng)性。對(duì)于s∈S,s ~is成立,稱(chēng)為自反性。對(duì)于s, q∈S,如果s ~iq,那么q ~is,稱(chēng)為對(duì)稱(chēng)性。
性質(zhì)三:{>>i, >i, ~i}滿(mǎn)足完備性。對(duì)于s, q∈S,s>>iq,q>>is,s>iq,q>is,s ~iq,必有一個(gè)滿(mǎn)足。
如果偏好信息沒(méi)有考慮決策者對(duì)待某一狀態(tài)喜好的程度,則強(qiáng)度偏好結(jié)構(gòu)退化為簡(jiǎn)單偏好。
2.3 強(qiáng)度偏好下的穩(wěn)定性
Hamouda等[13-14]給出了強(qiáng)度偏好下的四種標(biāo)準(zhǔn)穩(wěn)定性的定義:納什穩(wěn)定(Nash)、一般超理性穩(wěn)定(GMR)、對(duì)稱(chēng)超理性穩(wěn)定(SMR)和序列穩(wěn)定(SEQ)。這四種標(biāo)準(zhǔn)穩(wěn)定性定義的后三個(gè)穩(wěn)定性(GMR、SMR和SEQ)可以根據(jù)被對(duì)手反擊的程度被區(qū)分為強(qiáng)穩(wěn)定性(SGMR、SSMR和SSEQ)和弱穩(wěn)定性(WGMR、WSMR和WSEQ)。由于Nash穩(wěn)定沒(méi)有涉及到對(duì)手的反擊,因此在Nash穩(wěn)定下是沒(méi)有定義拓展的,即強(qiáng)穩(wěn)定性和弱穩(wěn)定性。強(qiáng)度偏好下四種標(biāo)準(zhǔn)穩(wěn)定性的定義及GMR穩(wěn)定、SMR穩(wěn)定和SEQ穩(wěn)定各自拓展的強(qiáng)穩(wěn)定性及弱穩(wěn)定性定義詳見(jiàn)Hamouda等[13-14]。
3 基于策略?xún)?yōu)先權(quán)排序法的強(qiáng)度偏好 序列獲取
3.1 簡(jiǎn)單偏好序列的獲取
關(guān)于簡(jiǎn)單偏好的排序方法,目前主要有三種方法[15]:策略加權(quán)平均法(為Option Weighting)、策略?xún)?yōu)先權(quán)排序法(Option Prioritizing)和直接狀態(tài)排序法(Direct Ranking)。下面介紹策略?xún)?yōu)先權(quán)排序法。
在使用策略?xún)?yōu)先權(quán)排序法求取簡(jiǎn)單偏好序列時(shí),對(duì)于每個(gè)決策者,沖突分析者需要給出一個(gè)由一些聲明(Statements)所組成的次序集合,聲明由一些策略編號(hào)和邏輯關(guān)系符號(hào)構(gòu)成。在一個(gè)特定狀態(tài)s∈S處,每個(gè)聲明Ω取一個(gè)值,T或F。如果Ω(s)=T,表明狀態(tài)s滿(mǎn)足該聲明;否則Ω(s)=F,狀態(tài)s不滿(mǎn)足該聲明。在該次序集合中,出現(xiàn)越早的聲明會(huì)被認(rèn)為擁有越大的優(yōu)先權(quán)。聲明可以是非條件形式,條件形式或者雙條件形式的,聲明的各種形式及其組成詳見(jiàn)Fang Liping等[15]。
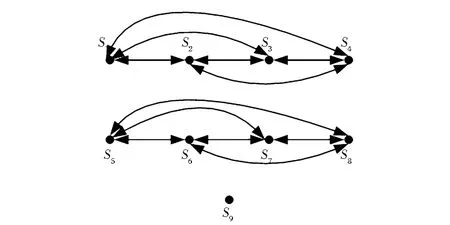
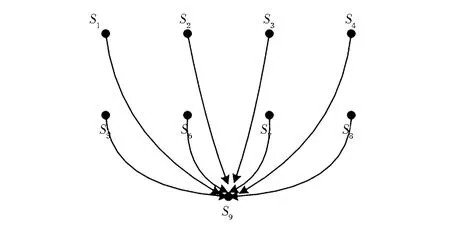
對(duì)于決策者i,通過(guò)給每個(gè)狀態(tài)設(shè)定一個(gè)“分值”Ψ(s)來(lái)對(duì)這些狀態(tài)按照分值從大到小的順序進(jìn)行排序。現(xiàn)假設(shè)k為給出聲明的數(shù)量,Ψj(s)為狀態(tài)s基于聲明Ωj的增分值,0 (1) 則各狀態(tài)的分值為: (2) 策略?xún)?yōu)先權(quán)排序法不能夠捕捉?jīng)Q策者全面的偏好信息。因此,在求解決策者偏好信息時(shí),通常先使用策略?xún)?yōu)先權(quán)排序法求解初始偏好信息,然后再使用直接狀態(tài)排序法對(duì)初始偏好信息進(jìn)行完善,得出最終的偏好信息。 3.2 強(qiáng)度偏好序列的獲取 假設(shè)根據(jù)沖突背景分析出決策者i∈N有k個(gè)聲明Ω1,Ω2,…, Ωk,k≥1。在公式(1)中,當(dāng)Ωj(s)=T時(shí),稱(chēng)Ψj(s)=2k-j為聲明Ωj對(duì)應(yīng)的權(quán)重,記為Wj。本文擴(kuò)展的策略?xún)?yōu)先權(quán)排序法用于獲取決策者i的強(qiáng)度偏好序列的過(guò)程如下所示。 將決策者i對(duì)某些狀態(tài)的強(qiáng)烈偏好或強(qiáng)烈厭惡程度反映到對(duì)相應(yīng)聲明的強(qiáng)烈偏好或強(qiáng)烈厭惡程度上來(lái)。對(duì)于Ω1,Ω2,…,Ωk,假設(shè)決策者i對(duì)Ωl有強(qiáng)烈的偏好,1≤l≤k。如果1≤l 調(diào)整規(guī)則1:Ω1,Ω2,…, Ωl對(duì)應(yīng)的權(quán)重為在原權(quán)重的基礎(chǔ)上加上2k,其余聲明對(duì)應(yīng)的權(quán)重保持不變,即: 現(xiàn)假設(shè)決策者i對(duì)Ωl1,Ωl2,…,Ωlg的偏好程度非常強(qiáng)烈,1≤ l1< l2<…< lg≤k,那么,各聲明對(duì)應(yīng)的權(quán)重可以按照調(diào)整規(guī)則2給予調(diào)整: 調(diào)整規(guī)則2:考慮Ωlg,按照調(diào)整規(guī)則1有: 相應(yīng)地,在Ωlg后面添加符號(hào)“&M”,即Ωlg&M; 考慮Ωlg-1,按照調(diào)整規(guī)則1有: 按照相同方式,一直調(diào)整到考慮Ωl1為止,即 (3) 此時(shí)公式(1)變?yōu)椋?/p> (4) 根據(jù)公式(2),(3),(4)求出所有可行狀態(tài)的分值,然后根據(jù)求得的分值對(duì)這些狀態(tài)進(jìn)行偏好排序。具體的強(qiáng)度偏好排序步驟如下: 第一步:對(duì)這些狀態(tài)按照相應(yīng)分值從大到小的順序排列成一個(gè)狀態(tài)序列Q。 第二步:根據(jù)定義2,對(duì)狀態(tài)序列Q中任意相鄰兩個(gè)狀態(tài)用符號(hào)>>i,>i或~i連接。一直到Q中任意相鄰兩個(gè)狀態(tài)均用符號(hào)>>i,>i或~i連接為止,得出帶有符號(hào)的狀態(tài)偏好序列P(Q)。 第三步:運(yùn)用直接狀態(tài)排序法對(duì)狀態(tài)偏好序列P(Q)中用符號(hào)~i連接起來(lái)的相鄰兩個(gè)狀態(tài)進(jìn)行重新排序,得出決策者的最終偏好序列。 表1 蘭州水污染沖突事件的可行狀態(tài) 定義2 對(duì)于Q中任意相鄰兩個(gè)狀態(tài)s∈S和q∈S,假設(shè)Ψ(s) ≥Ψ(q),那么有 推論1 如果假設(shè)>>或>成立,意味著?成立,也就是說(shuō)強(qiáng)度偏好退化為簡(jiǎn)單偏好。此時(shí),公式(4)與公式(1)一致。 從推論1看出,本研究成果擴(kuò)大了現(xiàn)有簡(jiǎn)單偏好下圖模型沖突分析理論的研究成果,將現(xiàn)有理論應(yīng)用于更為復(fù)雜的沖突模型中。 4.1 “蘭州水污染事件”的背景描述 近年來(lái),我國(guó)經(jīng)濟(jì)增長(zhǎng)突飛猛進(jìn),但同時(shí)環(huán)境問(wèn)題日益嚴(yán)重,頻頻爆發(fā)。今年4月10日,蘭州發(fā)生自來(lái)水苯超標(biāo)事件。苯是一種石油化工基本原料,在常溫下為透明液體,有毒,也是一種致癌物質(zhì)。國(guó)家限制自來(lái)水中苯的含量為10微克/升。11日15時(shí)許,甘肅官方通報(bào),蘭州市威立雅水務(wù)公司報(bào)告稱(chēng),10日17時(shí)出廠水檢測(cè)苯含量118微克/升,11日凌晨2時(shí),檢測(cè)值為200微克/升。根據(jù)蘭州“4·11”事件應(yīng)急處置領(lǐng)導(dǎo)小組通報(bào)的信息,此次事故由自來(lái)水廠周邊的地下含油污水引發(fā)。含油污水來(lái)自中石化蘭州分公司原料動(dòng)力廠1987年和2002年兩次爆炸事故遺留的廢渣。早在一二十年前,就有專(zhuān)家建議應(yīng)該將中石化蘭州分公司等污染企業(yè)整體搬遷。15日,蘭州“4·11”事件應(yīng)急處置領(lǐng)導(dǎo)小組曾通報(bào)說(shuō),合資企業(yè)、蘭州威立雅水務(wù)公司在此次事件中存在監(jiān)管不力的問(wèn)題。在水資源專(zhuān)家、中國(guó)農(nóng)業(yè)科學(xué)院農(nóng)業(yè)資源與農(nóng)業(yè)區(qū)劃研究所委員會(huì)成員看來(lái),管道是供水企業(yè)運(yùn)營(yíng)的重要組成部分,供水公司要對(duì)其進(jìn)行維護(hù)、確保安全,出了問(wèn)題當(dāng)然由供水公司來(lái)承擔(dān)。但更換管道的費(fèi)用巨大,企業(yè)不愿意承擔(dān),總是修修補(bǔ)補(bǔ),難以徹底化解風(fēng)險(xiǎn)。 4.2 “蘭州水污染事件”的沖突建模 4.2.1 決策者和方案 針對(duì)本次沖突事件,本文提煉出三個(gè)決策者:蘭州威立雅水務(wù)公司(DM1)、地方政府(DM2)和中石化蘭州分公司(DM3)。 對(duì)于蘭州威立雅水務(wù)公司,其主要目的是避免造成自身的經(jīng)濟(jì)消耗,它有一個(gè)策略: 1.改造設(shè)備:花費(fèi)成本對(duì)管道與壓力設(shè)備進(jìn)行修理改造。 對(duì)于地方政府,其主要目的是增加政府財(cái)政收入并同時(shí)注重環(huán)境的保護(hù),它有兩個(gè)策略: 2.支持遷址:迫于環(huán)保壓力,出臺(tái)政策并部分撥款令中石化蘭州分公司遷址至新區(qū); 3.支持改造設(shè)備:對(duì)蘭州威立雅公司施加壓力令其修理改造管道與壓力設(shè)備。 對(duì)于中石化蘭州分公司,其主要目的是繼續(xù)開(kāi)發(fā)當(dāng)?shù)刎S富資源,增加收入,它有一個(gè)策略: 4.遷址:遷址至新區(qū)。 4.2.2 可行狀態(tài)集 從邏輯上看,總共有24種狀態(tài),即16種狀態(tài)。但事實(shí)上,如果中石化蘭州分公司選擇遷址,無(wú)論其他兩個(gè)決策者選擇什么樣的策略,均會(huì)解決當(dāng)前的水污染問(wèn)題。所以狀態(tài)s9實(shí)際上包含了8種狀態(tài)。因此,最后此次沖突事件共包含9種狀態(tài),如表1所示。其中,“Y”表示決策者選擇該策略,“N”表示決策者放棄該策略,“—”表示既可以是“Y”,也可以是“N”。 4.2.3 狀態(tài)轉(zhuǎn)移圖 圖1、2和3分別描述了DM1、DM2和DM3的狀態(tài)轉(zhuǎn)移圖模型。圓點(diǎn)表示9種可行狀態(tài),弧的箭頭方向表示由初始狀態(tài)轉(zhuǎn)移到可達(dá)狀態(tài)。在圖中,有些箭頭是雙向的,表示狀態(tài)之間可逆;有些箭頭是單向的,表示狀態(tài)之間不可逆。 圖1 DM1的狀態(tài)轉(zhuǎn)移圖模型 圖2 DM2的狀態(tài)轉(zhuǎn)移圖模型 圖3 DM3的狀態(tài)轉(zhuǎn)移圖模型 4.2.4 強(qiáng)度偏好信息 根據(jù)案例背景,分析出三個(gè)決策者具體的偏好聲明及相應(yīng)的解釋?zhuān)绫?所示。 下面以求解DM1的強(qiáng)度偏好序列為例。根據(jù)表2中給出的聲明及公式(2),(3),(4)求解針對(duì)DM1的各個(gè)狀態(tài)的分值,結(jié)果為: Ψ(s1)=28;Ψ(s2)=29;Ψ(s3)=0;Ψ(s4)=1; Ψ(s5)=0;Ψ(s6)=1;Ψ(s7)=4;Ψ(s8)=5;Ψ(s9)=2。 根據(jù)3.2節(jié)中強(qiáng)度偏好的排序步驟,得出DM1的初始強(qiáng)度偏好序列為: s2>1s1>>1s8>1s7>1s9>1s4~1s6>1s3~1s5 然后運(yùn)用直接狀態(tài)排序法對(duì)其進(jìn)行完善,為: s2>1s1>>1s8>1s7>1s9>1s6>1s4>1s5>1s3 按照相同方法,可求得DM2和DM3的強(qiáng)度偏好序列分別為: s7>2s5>2s8>2s6>>2s3>2s1>2s4>2s2>>2s9 s7>3s5>3s3>3s1>3s8>3s6>3s4>3s2>>3s9 表2 蘭州水污染沖突事件中各決策者的聲明及相關(guān)說(shuō)明 4.3 穩(wěn)定性分析 表3(1)與(2)分別為強(qiáng)度偏好下,標(biāo)準(zhǔn)穩(wěn)定性、強(qiáng)穩(wěn)定性、弱穩(wěn)定性定義下各狀態(tài)的均衡情況。“√”表示在穩(wěn)定性定義下,某狀態(tài)是均衡解。表中“E”為Equilibrium的縮寫(xiě),代表均衡。 表3(1)中,狀態(tài)7,9為Nash、GMR、SMR、SEQ穩(wěn)定性定義下的均衡解,狀態(tài)1,2,4,5,6,8為GMR、SMR穩(wěn)定性定義下的均衡解。表3(2)中,狀態(tài)7,9為SGMR、SSMR、SSEQ穩(wěn)定性定義下的均衡解,狀態(tài)5,6,8為SGMR、SSMR穩(wěn)定性定義下的均衡解,此時(shí)1,2,4在任何穩(wěn)定性定義下不再是均衡解了。對(duì)于狀態(tài)1,2,4,DM1沒(méi)有去改造設(shè)備,而DM2強(qiáng)烈希望的是DM1去改造設(shè)備,并且與此同時(shí)更加強(qiáng)烈希望DM3不遷址。所以在DM1沒(méi)能及時(shí)地對(duì)設(shè)備進(jìn)行改造時(shí),DM2將會(huì)對(duì)其施加壓力令其改造設(shè)備,也就是狀態(tài)3。對(duì)于狀態(tài)7,由于DM2對(duì)DM1施加壓力,DM1迫于壓力對(duì)設(shè)備進(jìn)行改造,與此同時(shí),DM3沒(méi)有選擇遷址,這是DM2非常希望看到的一種局勢(shì)。狀態(tài)5,6,8在SSEQ穩(wěn)定性定義下不是均衡解,因此不是沖突事件最終得以解決的最優(yōu)解。綜上可知,能夠解決此次水污染事件的均衡解為狀態(tài)7、9。然而對(duì)于狀態(tài)9,DM3可能由于社會(huì)輿論的壓力以及隨著事態(tài)的發(fā)展對(duì)其造成影響而選擇了遷址,這是DM2非常不希望看到的,也是DM3最不希望去做的。因此,狀態(tài)7這個(gè)均衡解可以很好的解決沖突,使沖突各方均找到了一個(gè)滿(mǎn)意解。 表3 強(qiáng)度偏好下的沖突均衡解 表3 (2)強(qiáng)穩(wěn)定性、弱穩(wěn)定性定義下的沖突均衡解 圖4給出了由初始狀態(tài)1向均衡狀態(tài)7的演化路徑示意圖。在蘭州威立雅水務(wù)公司沒(méi)有自覺(jué)改造設(shè)備時(shí),當(dāng)?shù)卣疄榱吮M快地解決當(dāng)前水污染問(wèn)題并防止沖突期間中石化蘭州分公司選擇遷址,會(huì)及時(shí)地對(duì)威立雅水務(wù)公司施加壓力令其改造設(shè)備,使得當(dāng)前蘭州水污染事件得以解決。 圖4 蘭州水污染事件的演化路徑示意圖 本文將簡(jiǎn)單偏好下的策略?xún)?yōu)先權(quán)排序法擴(kuò)展到強(qiáng)度偏好,并將擴(kuò)展后的方法運(yùn)用到“蘭州水污染”沖突事件中,求解出各決策者的強(qiáng)度偏好信息,分析了各個(gè)狀態(tài)的穩(wěn)定性,求出各種情況下的均衡解,幫助政府、企業(yè)做出正確的決策,促進(jìn)經(jīng)濟(jì)與環(huán)境的協(xié)調(diào)發(fā)展。論文擴(kuò)展的策略?xún)?yōu)先權(quán)排序法能夠?qū)F(xiàn)有的強(qiáng)度偏好圖模型沖突分析理論應(yīng)用到更為復(fù)雜的沖突模型中,幫助決策者更好地認(rèn)識(shí)和解決沖突,促進(jìn)沖突各方更好地和平共處,達(dá)到一種“雙贏”或“多贏”的局面,從而維護(hù)沖突所在系統(tǒng)的良好運(yùn)轉(zhuǎn)和發(fā)展。 [1] Von Neumann J, Morgenstern O. The theory of games and economic behavior[M].Princeton,New Jersey:Princeton University Press, 1944. [2] Howard N. Paradoxes of rationality: Theory of metagames and political behavior[M].Cambridge, MA: MIT Press, 1971. [3] Kilgour D M, Hipel K W, Fang Liping. The graph model for conflicts[J].Automatica, 1987, 23(1): 41-55. [4] Fang Liping, Hipel K W, Kigour D M. A decision support system for interactive decision making: The graph model for conflict resolution[M].New York: Wiley, 1993. [5] Getirana A, Malta V D. Decision process in a water use conflict in brazil[J].Water Resources Management, 2008, 22(1): 103-118. [6] Inohara T, Hipel K W, Walker S. Conflict analysis approaches for investigating attitudes and misperceptions in the war of 1812[J].Journal of Systems Science and Systems Engineering, 2007, 16(2): 181-201. [7] Hipel K W, Walker S B. Conflict analysis in environmen- tal management[J].Environmetrics, 2011, 22(5): 279-293. [8] 韓雪山, 徐海燕. 基于圖模型的復(fù)雜產(chǎn)品過(guò)程沖突研究[J].現(xiàn)代管理, 2012,2(1): 39-44. [9] 劉德海. 群體性突發(fā)事件中政府機(jī)會(huì)主義行為的演化博弈分析. [J].中國(guó)管理科學(xué), 2010, 18(1): 175-183. [10] 陳珍, 費(fèi)軍. 基于演化博弈視角下企業(yè)工資集體協(xié)商機(jī)制的研究[J].中國(guó)管理科學(xué), 2012,20(SI): 1-7. [11] 浦徐進(jìn), 吳亞, 路璐, 等. 企業(yè)生產(chǎn)行為和官員監(jiān)管行為的演化博弈模型及仿真分析[J].中國(guó)管理科學(xué), 2013,21(SI): 390-396. [12] 趙禮強(qiáng), 徐家旺. 基于電子市場(chǎng)的供應(yīng)鏈雙渠道沖突與協(xié)調(diào)的契約設(shè)[J].中國(guó)管理科學(xué), 2014, 22(5):61-68. [13] Hamouda L, Kilgour D M, Hipel K W. Strength of preference in the graph model for conflict resolution [J].Group Decision and Negotiation, 2004, 13(5): 449-462. [14] Hamouda L, Kilgour D M, Hipel K W. Strength of preference in graph models for multiple-decision-maker conflicts [J].Applied Mathematics and Computation, 2006, 179(1): 314-327. [15] Fang Liping, Hipel K W, Kigour D M, et al. A decision support system for interactive decision making-part 1: Model formulation[J].IEEE Transactions on Systems Man and Cybernetics Part C-Applications and Reviews, 2003, 33(1): 42-55. [16] Xu Haiyan, Kilgour D M, Hipel K W. An integrated algebraic approach to conflict resolution with three-level preference[J].Applied Mathematics and Computation, 2010, 216 (3): 693-707. [17] Xu Haiyan, Hipel K W, Kilgour D M. Multiple levels of preference in interactive strategic decisions [J].Discrete Applied Mathematics, 2009, 157(15): 3300-3313. [18] 韓雪山. 基于沖突分析圖模型的結(jié)盟穩(wěn)定性研究[D].南京:南京航空航天大學(xué),2013. Research on Option Prioritization for Strength of Preference Based on the Graph Model for Conflict Resolution HOU Yu-hang, XU Hai-yan (College of Economics and Management, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China) Strength of preference is incorporated into the graph model for conflict resolution (GMCR) to enhance intensity of relative preference. It is very important to obtain a ranking of strength of preference based on option prioritization for modeling module. The option prioritization approach for simple preference is extended to strength of preference in this paper. The proposed approach is employed to the “Water Pollution Conflict in Lanzhou” in which there are three decision makers with strength of preference. The conflict model is established and then the process of this conflict's negotiations and consultations is simulated. Finally, the equilibria of this model are obtained using the decision support system based on GMCR. The results from this research provide a valuable view for the sustainable development of China's economy. graph model for conflict resolution; strength of preference; option prioritizing; Water Pollution Conflict in Lanzhou 2014-07-12; 2014-12-30 國(guó)家自然科學(xué)基金資助項(xiàng)目(71471087);江蘇省高校哲學(xué)社會(huì)科學(xué)研究重點(diǎn)項(xiàng)目(2012ZDIXM014) 簡(jiǎn)介:侯宇航(1991-),男(漢族),安徽淮北人,南京航空航天大學(xué)經(jīng)濟(jì)與管理學(xué)院,碩士生,研究方向:沖突分析,E-mail:596811629@qq.com. C934 A 1003-207(2016)09-0064-07 10.16381/j.cnki.issn1003-207x.2016.09.008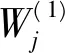
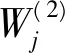
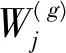

4 “蘭州水污染事件”的沖突模型





5 結(jié)語(yǔ)

