基于勢函數場模型的密集人群結隊疏散方法

菅肖霞,張小寧

(同濟大學經濟與管理學院,上海200092)

基于勢函數場模型的密集人群結隊疏散方法

菅肖霞,張小寧*

(同濟大學經濟與管理學院,上海200092)

為再現坡度設施中密集人群的擠壓倒地現象,建立一種勢函數場元胞自動機模型.該模型采用耦合行人之間擠壓作用力場的坡度人行設施勢函數場作為人群行走方向的“導航圖”.利用模型分析斜坡角度、人群密度與行人擠壓倒地現象之間的作用機制,提出兩兩結隊行走策略可以減少倒地人數.模擬結果表明采用兩兩結隊行走策略時倒地人數不超過總人數的10%.

勢函數場;元胞自動機;擠壓;倒地;兩人結伴行走;坡度

1 引 言

近年來,我國舉辦文體娛樂活動的規模和數量不斷地增加,組織者對于活動場所的容量、結構及其周圍的交通條件均有不同程度的需求,因此,改建舊式娛樂活動場所,同時新建大規模的現代化設施成為一種發展趨勢.然而,在改建和新建過程中難免出現新舊設施出入口過渡區域不在同一水平面上的情形,需采用坡度出入口設施進行銜接.從而引發出此類設施中的安全行走問題,尤其在下坡出入口處,坡度越陡,行人的穩定性越差,隨著人群密度的增加,行人之間的推擠作用增強,與水平設施相比,密集人群在該類設施中更加容易被推倒.

解決上述問題的關鍵是模擬行人推擠作用過程及擠壓倒地現象,分析行人個體之間的非線性作用對集群現象的影響,最終提出科學有效的坡度人行設施安全疏散方法,即在人群推擠作用力達到行人個體可承受的最大推力之前,實時對行人行走策略進行指導,避免個別行人倒地而引發一系列踩踏事故.

目前,用于模擬行人運動的模型主要包括:社會力模型、連續流體力學模型以及元胞自動機模型.社會力模型[1]是將行人視為有限大小的二維粒子,將行人對周圍環境的反應以及行人與行人之間的各種內在動機類比為各種作用力,行人在力的作用下運動,且遵循牛頓第二定律.該模型可以模擬行人流的出口處呈“拱形”擁堵現象、通道中相向行人流的成行現象、瓶頸口處相向行人流的振蕩現象、交叉行人流的成帶現象以及“時走時停”現象等不同的行人流自組織現象[2,3].此類模型的優勢在于充分考慮行人個體之間的作用力,缺點是由此而造成的模型計算復雜度高.行人流連續流體力學模型[4-6]將行人群體假設為均勻連續流體介質,每個行人類比為具有相同特性的流體質點,采用可壓縮流體力學方程組,描述行人流的速度、密度、流量這類宏觀物理量之間的關系.該模型不能直接描述行人個體之間的微觀相互作用.行人流元胞自動機模型[7,8]是在具有離散且有限狀態的元胞空間和離散時間段上,按照一定的局部規則更新整個區域中的元胞狀態,模擬人群運動變化過程的動力學系統.此類模型中發展較為顯著的是Burstedde等[8]提出的地場元胞自動機模型,模型將地場作為行人運動的虛擬“導航圖”,行人的行走規則依據靜態地場耦合動態地場來確定,其中靜態地場表征行人出發地與目的地距離,動態地場表征行人之間的相互作用.此類模型計算復雜度低,可以直接描述行人個體之間的微觀作用力,再現擁堵現象、瓶頸效應、出口處成拱現象、從眾效應以及自組織成行現象等典型的行人流特征,是后續發展行人流模型的基礎之一.

在地場元胞自動機模型的基礎上,大量的研究工作集中于從行人行走路徑選擇角度改進地場計算方法[9-11];從復雜場景中行人運動行為角度擴展地場模型,模擬具有不同轉角長廊中的疏散[12,13],多出口疏散[14]以及地鐵站內交織行人流的發展過程[15];研究行人流在具有坡度出入口設施中的擠壓作用[16];考慮偏向行走[17,18]、行人可視度的變化對行人運動過程的影響[12,19];行人結伴行為對于行人流疏散時間的影響[20,21]等.另外,還有結合連續流體力學模型、社會力模型和元胞自動機模型優勢而發展的混合模型.宋衛國等[22]以社會力模型為參考,在元胞自動機模型中考慮行人之間的擠壓、排斥作用力.Zhang等[23]結合行人流連續模型中的行人選擇沿所需行走費用減少最快的方向行走的策略,提出勢函數場元胞自動機模型.

綜上所述,研究具有斜坡出入口人行設施中的行人流問題以及相關管理措施的工作較缺乏.另外,行人結隊行走方式較為普遍,是行人自發增加抗壓能力的可行性措施,但是目前已有的研究工作[20,21,24]將其作為影響人群流量的行人特征,未考慮到結隊行走方式在抵抗推擠作用中的有效性.本文將研究具有坡度人行設施中,過度擁堵人群擠壓倒地現象的成因,以及探究通過何種結隊行走的方式自發增加抗壓能力,避免群體性擠壓倒地踩踏事故的發生.

在正常情況下,行人都具有一定的認知能力,在密集區域時,行人之間的空余空間較少、身體接觸較多,行人不能按照其自身的意愿移動到渴望的位置,行走舒適度降低.行人認為只要將其前方行人推走,其本身即可盡快到達目的地,從而遠離不舒適的擁擠區域.因此,每個行人產生推力,推力由一個行人傳遞給另一個行人,隨著時間的增加,前面的行人承受其后方人群的聚集推力.行人在聚集力作用下,擁擠程度增加,形成密集度越大推擠力越大的惡性循環;聚集擁堵現象長時間得不到解決,體弱者將窒息倒地,必然引起人群恐慌,最終造成嚴重的踩踏事故.針對這類安全隱患,在前期工作[16]的基礎上,通過量化行人之間的推壓作用力,簡化模型規則,建立耦合坡度影響的費用勢函數場元胞自動機模型,模擬高密度行人流的過度擁擠、倒地現象,探究行人之間的微觀作用機理.

考慮到行人在高密度擁擠的情況下,從眾心理更加明顯,組織管理者穩定的情緒、鎮靜的行為可以有效對抗人群的不安和恐慌.本文充分利用人群與組織管理者博弈過程中的從眾心理作為安全管理設計的前提,提出實時指導行人采用兩人結隊行走的方式自行減除倒地現象的發生.將兩人結隊行走措施量化為參數形式,引入建立的模型,定量地研究兩人結隊行走措施的有效性.

2 耦合擠壓作用力場的勢函數場元胞自動機模型

本文研究在具有坡度人行設施中行人流的安全疏散問題.考慮到正常情況下行人具有一定的認知能力,本文采用連續模型中行人移動方向選擇的最優路徑策略,即行人沿時間花費最少的路徑到達目的地,也就是沿時間費用勢函數的負梯度方向移動.選用這一最優路徑選擇策略,可以減少行人在選擇目標位置時的盲目性和隨機性,提高元胞自動機模型在模擬正常情況下的可行性,同時提高模型的計算效率.加之,行人之間的推擠作用是形成行人擠壓踩踏現象的重要原因,因此,本文也結合社會力模型中描述行人與外界環境、行人個體之間的相互作用方式,量化行人個體之間的擠壓作用力,建立耦合擠壓作用力場的勢函數場元胞自動機模型.本節主要闡述擠壓作用力場耦合受坡度影響的費用勢函數場元胞自動機模型的構造過程,其中包括具有坡度影響的費用勢函數場、行人之間相互擠壓作用力場以及模型的更新規則和安全行走方法的構造.

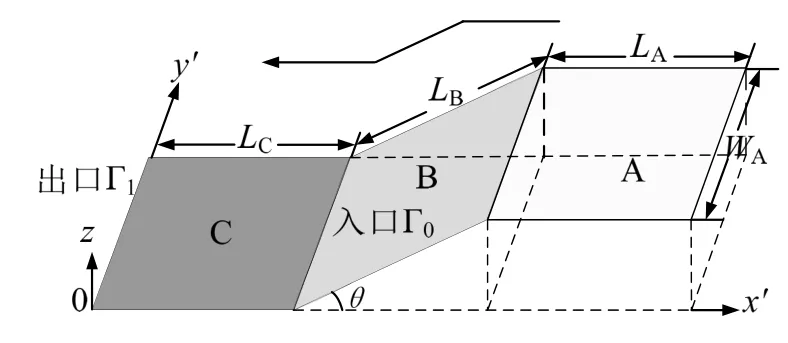
圖1 有坡度行人設施示意圖Fig.1 Illustration of the walking domain with a ramp

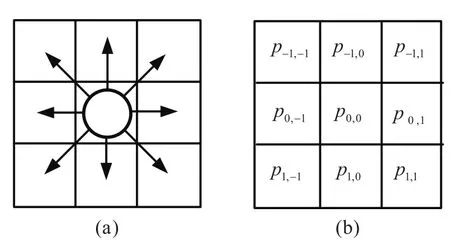
圖2 (a)一個被占據的元胞(0,0)及其8個鄰居;(b)相應的移動概率Fig.2 (a)An occupied cell(0;0)and its eight neighboring cells;and(b)the corresponding probabilities

2.1 具有坡度影響的勢函數場

模型中的勢函數場是行人運動的“導航圖”,行人沿費用勢減小的方向移動,由于行人移動區域并非平面區域,為了計算該區域上的勢函數場值,在時刻t,首先,將區域拉伸為平面區域Ω,Ω的出口同為Γ1,平面區域Ω與三維區域的子區域C重疊.均勻劃分區域Ω,保持平面區域Ω與三維區域的元胞大小和個數均一致.在Ω上,計算勢函數場φ(x,y,t),其中(x,y)表示元胞位置;其次,引入坡度系數ω(x,y,θ)對φ(x,y,t)進行重構,得到含坡度區域上的勢函數場(x,y,t,θ).具體求解步驟如下.

1)求解平面區域Ω上的勢函數

假設τ(x,y,t)≥0為費用分布函數,即單位距離上的時間費用,在固定時刻t,平面行走區域Ω中任意位置(x,y)的勢函數φ(x,y,t)是關于費用分布函數τ(x,y,t)的泛函,行人從(x,y)到某個目的地位置(x0,y0)∈Γ1的總費用為

在式(1)中,將(x,y)到(x0,y0)的積分路徑表示為單位向量(x′(s),y′(s))指向積分方向.為了便于說明,不妨將位置(x0,y0)完全等同于集合Γ1.

根據場論中積分與原函數之間的關系,要保證勢函數φ(x,y,t)為單值函數,只需假設式(1)的積分與路徑無關,即要求φ(x,y,t)滿足條件

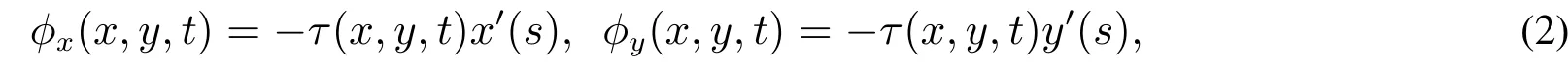
由此可得Eikonal方程

而且,方程(1)的可積性暗含φ(x0,y0,t)=0,(x0,y0)∈Γ1,是方程(3)的邊界條件.因此,當假設φ(x,y,t)≥0時,Eikonal方程邊值問題的解存在唯一,詳細證明可參考文獻[23].

以上理論推導表明,在固定時刻t,任何位置(x,y)處行人在無推擠作用力的情況下,渴望的移動方向為此外,費用分布函數τ(x,y,t)滿足[5,23,27]τ(0)=1,τ′(ρ)＞0,0≤ρ≤1,ρ=ρ(x,y,t)為密度分布函數,這里采用以(x,y)為中心,包含至少25個元胞的子區域上的平均密度作為(x,y)處的密度.方程(3)在滿足邊界條件φ(x0,y0,t)=0, (x0,y0)∈Γ1下的解可采用快速步進法[28]求得.

采用φ(x,y,t)乘以坡度系數ω(x,y,θ),重構有坡度區域上的勢函數(x,y,t,θ),即

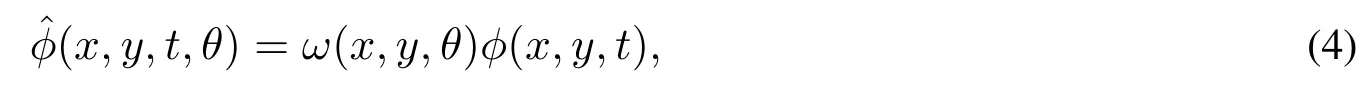
其中

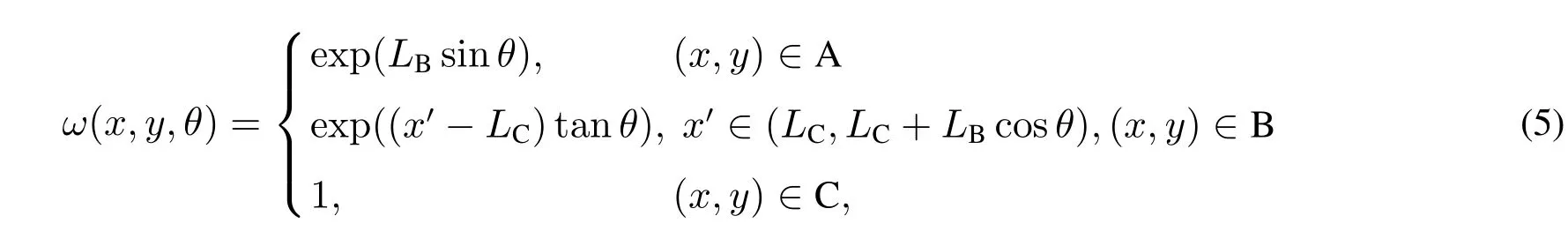
由ω(x,y,θ)的表達式(5)可知,利用ω(x,y,θ)≥1將平面上的勢函數φ(x,y,t)放大為三維區域上的勢函數(x,y,t,θ),其充分反映坡度對于勢函數值的強烈影響作用;ω(x,y,θ)定義為坡度角θ∈[0°,90°)的增函數,表明坡度角越大,受坡度影響的區域A和區域B上的勢函數值變化越大;注意到,當取定坡度角θ時,ω(x,y,θ)在子區域A和區域C上的值不同,事實上,盡管子區域A和區域C都是平面區域,但是它們位于不同的水平面上,坡度系數取值不同表示兩個子區域有高度差,區域A受到坡度的影響,其ω(x,y,θ)值大于1,相反地,區域C位于最低的水平面上,其ω(x,y,θ)為常數1,不受坡度角的影響.此外,(x,y,t,θ)和φ(x,y,t)具有相容性,即當θ=0°時,(x,y,t,θ)=φ(x,y,t).

2.2 擠壓作用力場

當行人處于密集人群時,每個行人被周圍行人包圍.在這種情況下,行人渴望盡快到達目的地,因此,行人有意識的推擠其前方行人,從而造成擠壓作用力的聚集增加.本小節通過引入聚集推力場模擬密集人群中行人之間擠壓力的作用效果.

在時刻t,當位置(x,y)處行人的無量綱密度為ρ(x,y,t)=1時,(x,y)處行人的周圍沒有空位置, (x,y)處行人所產生推力的大小為

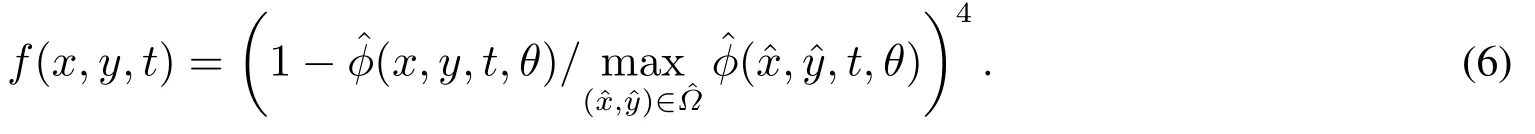
這里的推力大小f(x,y,t)并非真實行人推力的大小值,只反映推力的作用效果,表明行人所在位置的費用勢對行人所產生推力的影響程度.由式(6)可知,f(x,y,t)是勢場值(x,y,t,θ)的減函數,可以驗證這是合理的假設,事實上,當行人走到目的地附近時,其所在位置處的費用值遠比區域中的最大費用值小,此時,行人具有更強的動力去推擠其前方的行人;相反地,當行人當前的位置與目標位置相差很遠時,行人清楚地知道其周圍行人的分布狀況,推擠其他行人對于其盡快到達目的地的作用效果較小,因此,其產生的推力較小.由于行人產生推力是為了使其自身盡快到達目的地,推力的方向為沿費用勢(x,y,t,θ)減少最快的方向,即l(x,y,t)=(l1,l2)=-(x,y)/‖?‖,由此可得,在時刻t,(x,y)處行人所產生的推力為f(x,y,t)=f(x,y,t)l(x,y,t).

Fruin[29]的研究表明,行人產生的推力,由于行人之間的身體接觸,被不斷地由一個行人傳遞給另一個行人,本文將采用疊加每個時間步每個行人承受推力的方式模擬推力的傳遞和聚集過程.采用fadd(x,y,t)表示時刻t,在位置(x,y)處增加的推力,當(x,y)被行人占據,且其為另一個行人的渴望位置時,(x,y)處行人承受的推力fadd不為零,具體地來說,若(x,y)的某個鄰居位置(,)被行人占據,且此行人的渴望移動方向為l(,,t)=(x-,y-),(,)處行人產生的推力為f(,,t),此時推力f(,,t)被施加于(x,y)處行人身上,因此增加推力fadd(x,y,t)的大小為f(,,t),方向沿l(,,t);否則,fadd=0.

因此,時刻t,元胞(x,y)處行人承受的聚集推力為t-1時刻的聚集推力與增加的推力fadd(x,y,t)的向量和.聚集推力向量場F(x,y,t)定義為

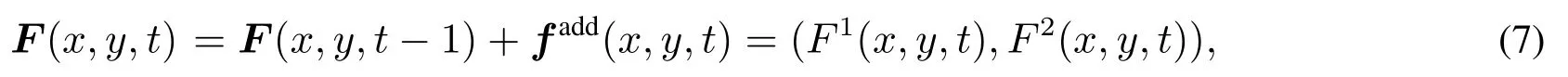
式(7)中第一個等號右端第一項表明隨著時間的不斷增加,推力的聚集過程;第二項表明每個時間步推力從一個行人到另一個行人身上的傳遞過程.式中F1(x,y,t)和F2(x,y,t)分別為F(x,y,t)沿x和y方向的分量,為了便于表述,采用‖F(x,y,t)‖=((F1(x,y,t))2+(F2(x,y,t))2)1/2表示F(x,y,t)的大小.

在密集型人群中,行人在力的作用下被推動前進,當行人累積承受的推力‖F(x,y,t)‖超過其可以忍受的最大力度（臨界值）時,行人可能會被推倒而受傷,此時受傷的行人將無法繼續移動.記F*(x,y,t)表示臨界值,注意到每個行人可承受的最大力度不同,若行人自身產生的推力大,則相應地其可承受的力度也會變大,因此假設F*(x,y,t)是每個行人可產生推力大小f(x,y,t)的增函數;另外,坡度角的大小也會影響行人可承受的力度,顯然地,當行人占據的位置越陡峭,行人越容易被推倒,可承受力度的臨界值越小.綜上,臨界值F*(x,y,t)為

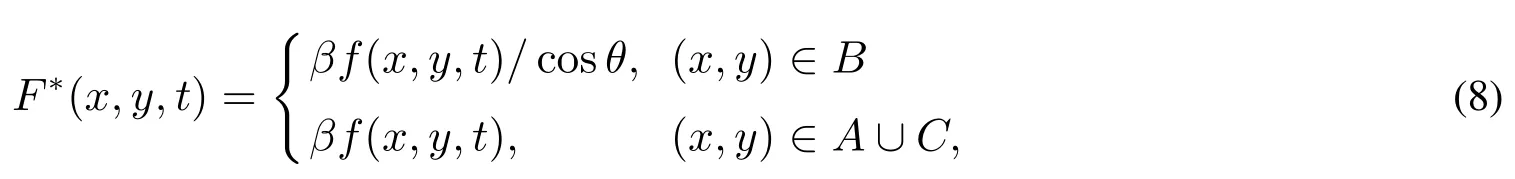
其中

從β的定義可知,β是坡度角θ的減函數,若θ=0°,β取到最大值,這表明在平坦的行走區域中,行人不容易被推倒,而隨著θ增大,β減小,行人容易被推倒.顯然地,該臨界值的定義不是唯一的,可以針對不同的場景,而采用不同的形式來深入研究人群動態.

為了避免行人承受的推力超過其臨界值時,行人被推倒,本文采用在單個行人承受的推力將達到其臨界值之前,指導其與同排的左或右單個行人采取手挽手的方式增加自身承受力.考慮到并排多人成組對于行人疏散流量的影響較大,本文只考慮兩人成組的情形.具體來說,分組時(x,y)處行人需要滿足的條件和措施為:(a)時刻t,(x,y)處行人不屬于任何小組;(b)(x,y)處行人承受的推擠力滿足γF*(x,y,t)＜‖F(x,y,t)‖＜F*(x,y,t),其中結隊參數γ∈(0,1)確保在行人被推倒之前采用安全結隊行走措施;(c)(x,y)處行人可以與同排左右鄰居中一個沒有結伴的行人(,)手挽手,若兩個鄰居都為單個行人,則等概率選擇其中之一;(d)(x,y)與其結伴的行人(,)形成兩人小組,行走過程中視為一個整體; (e)當單個行人左右鄰居都有各自小組,若(x,y)處行人左或右邊鄰接墻壁,該處行人可以采用扶墻的方式,否則,此行人將繼續獨自行走.

2.3 模型更新規則

從以上兩節的討論可知,在方程(3)中,引入預先設定的費用分布函數τ(x,y,t),利用數值方法求得方程(3)的數值解,并將解代入式(4),得到費用勢場(x,y,t,θ);而采用式(7)可以計算得到聚集力場F(x,y,t).下面將利用這兩個場確定模型規則:一方面利用勢函數場值,結合比較聚集推力‖F(x,y,t)‖和臨界值F*(x,y,t)的大小,確定行人可移動方向上的概率或行人被推倒受傷的概率,從而確定行人位置的更新規則;另一方面考慮到需要增加行人的抗擠壓能力避免倒地事故發生,將每兩個行人采用手挽手的措施量化為模型規則,從而定量地得出行人安全行走的位置更新規則.

本文在有無安全措施的兩種情況下,均采用隨機串行更新規則,即在每個時間步將所有行人隨機排序.采用此類隨機串行序列更新規則的優點是既從統計角度保證每個行人具有同等的優先權,又不必解決并行更新規則中行人位置沖突問題,又不影響模型再現行人運動規律.每個時間步將所有行人隨機排序后,利用勢函數場和聚集力場依次計算行人移動概率,確定行人移動方向,再利用移動后行人的新位置分布,更新勢函數場和擠壓作用力場,直至可移動行人離開行走區域或達到總計算時間.令(0,0)表示未受傷單個行人所占的元胞,從時刻t到t+1,行人位置更新規則、安全行走更新規則以及相應情形下聚集力傳遞過程的數學表述如下.

2.3.1 無安全措施情況下,行人的位置更新規則

1)行人位置隨機排序:在時刻t,將所有行人位置隨機排序的算法過程為

(a)記t時刻未受傷行人總數為Nt,顯然,

(b)行人在t時刻的位置是確定的,所有人的位置集合記為

(c)將標號序列{1,2,....,Nt},隨機重新排序后,得到行人的更新順序.

其中(i,j)∈S0,0={(i,j)|(i,j)為空,且|i-0|≤1,|j-0|≤1,(i,j)/=(0,0)},δi,j(0)≡((i,j)-(0,0))/di,j表示差商,di,j表示元胞(i,j)與(0,0)之間的距離;集合Sm的定義為Sm={(i,j)|δi,j(0)=,且表示集合Sm的元素個數.

其中rinjured是一個概率數,等概率取值0或1.此值可視為外界對于行人倒地的干擾因素,即當行人承受的擠壓作用力超過其可承受的臨界值時,行人可能倒地也可能不倒地.倒地時,位置(0,0)處行人以概率受傷倒在位置(i,j),若(i,j)/=(0,0),該行人倒在一個空位置上,此位置位于此行人受到的聚集推力的方向上;否則,該行人將倒在原位置.

2.3.2 考慮安全措施情況下,行人的位置更新規則

1)行人位置隨機排序:在時刻t,將每個兩人小組作為一個整體,對所有單獨行人和兩人小組隨機排序,算法的實現過程與2.3.1節中的1)同理.

2)行人兩兩結隊規則

(a)本文行人總體的行走趨勢為向左,行人面向左,(0,0)同排鄰居行人的位置為(1,0)和(-1,0),參照圖2(b)所示的位置標記,記與(0,0)處行人結伴行人的位置記為,其定義為

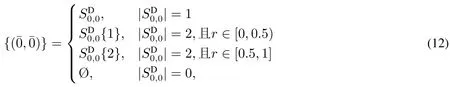
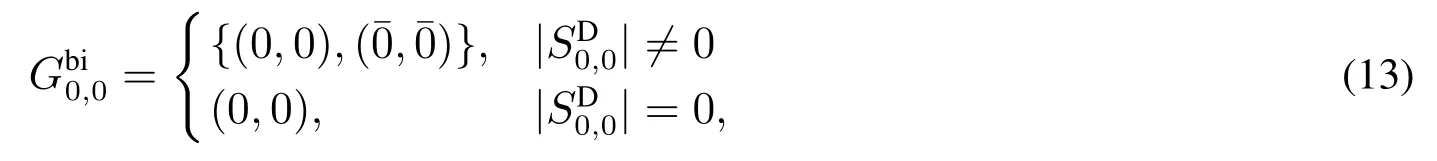
(b)支撐力大小更新為

(c)重新計算臨界值,即

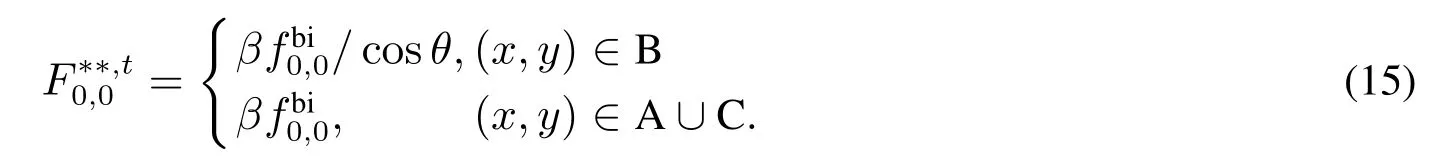
(i,j)∈表示小組的差商;集合的定義為表示集合的元素個數.

倒地行人被作為固定障礙物排除在移動系統之外,其受到的推力歸0;若小組成員之一倒地,另一行人將單獨行走,承受力恢復為其單獨時的承受力.

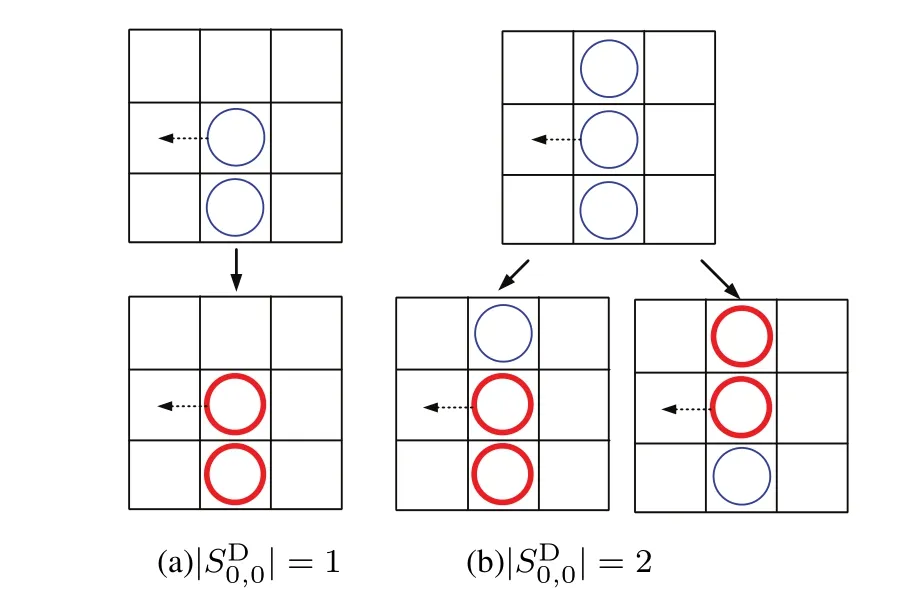
圖3 采用安全措施規則2.3.2的兩兩行人結隊方式示意圖Fig.3 Diagrammatic sketch of two-people-together strategy using rules 2.3.2

2.3.3 擠壓作用力場的傳遞規則

當t=0時,(0,0)處行人承受聚集力的初始值為0,即從時刻t到t+1,按照規則2.3.1或2.3.2,每個行人得到了更新位置,而且此位置唯一,不妨設(0,0)處行人的最終更新位置為(i*,j*),該行人在時刻t+1,或移動到此位置,或倒在此位置,此時,(0,0)處行人承受的聚集力也將跟隨行人移動到新位置(i*,j*)處,聚集擠壓力的傳遞過程為

以上為本文模型的更新規則和算法步驟,其計算與模擬過程均采用MATLAB語言編程實現.

3 倒地現象模擬

本節將采用規則2.3.1模擬再現無安全措施情況下,人群在具有坡度設施中的擠壓倒地現象.模型參數設置如下:行走區域的尺寸為LA=20,LB=5,LC=4,WA=WB=WC=6;費用分布函數取為[16,23]

其中g0=0.075,ξ=2.考慮到受傷倒地行人無法移動且阻礙未受傷行人前進,以下每次模擬運算的結束條件為人行設施中無可前進行人,且總時間不超過100個時間步.另外,理論上斜坡角度θ的取值范圍是[0°,90°),但實際中常見的坡度設施的角度最大約為35°,因此,模擬中采用的最大坡度角均為35°.為了減少模型中概率數對于模擬結果的影響,模擬數據均采取10次模擬結果的平均值.

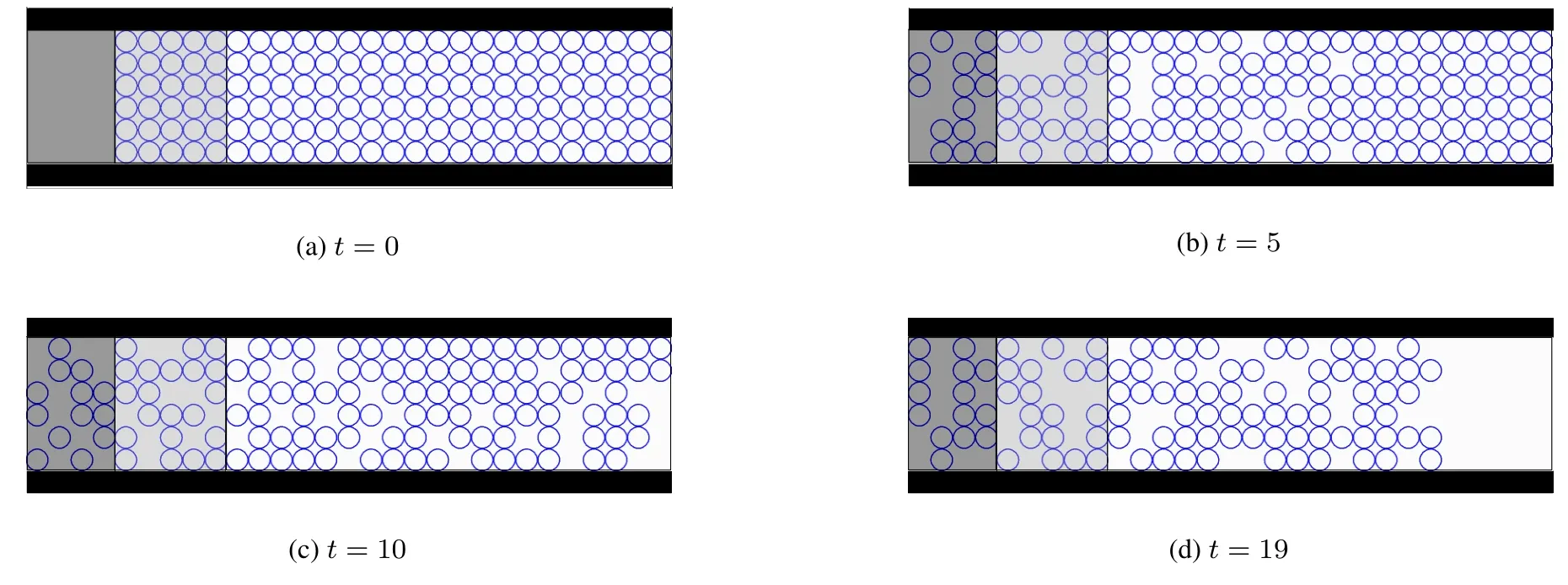
圖4 采用無安全措施規則2.3.1的模型模擬得到的行人疏散過程截圖(ρ0=1,θ=10°)Fig.4 Evacuation process simulated by the proposed model using rules 2.3.1 without the safe strategy(ρ0=1,θ=10°)

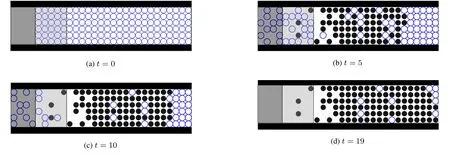
圖5 采用無安全措施規則2.3.1的模型模擬得到的行人疏散過程截圖(ρ0=1,θ=35°)Fig.5 Evacuation process simulated by the proposed model using rules 2.3.1 without the safe strategy(ρ0=1,θ=35°)

無安全措施情形下,具有坡度人行設施中行人疏散過程的截圖（拉伸在二維平面上）如圖4及圖5所示,其中每4個子圖分別為時刻(a)t=0;(b)t=5;(c)t=10;(d)t=19相應的截圖.圖4與圖5中的坡度角分別為θ=10°和θ=35°,初始行人密度均為ρ0=1,即實際密度為6.25ped/m2,區域A和區域B中此時共有150人.圖4(a)～4(d)表明在坡度較小時,行人可以保持安全行走無倒地現象發生;而圖5(a)～5(d)再現人群在坡度較大設施中的擠壓倒地現象.高密集人群聚集于具有較大坡度設施中,行人渴望盡快到達目的地,在無法順利前進的情況下,行人之間的推擠作用增強;且受坡度影響,行人的穩定性減弱,當前方行人無法承受巨大的推擠作用力倒地時,人群中出現“多米諾”效應,后方行人瞬間失去支撐,而相繼倒地,最終導致大量行人倒地.另外,從圖5(d)展示的模擬結果可知,在t=19之后,人群分布將保持在t=19時的狀態,大部分行人被推倒,人群后方的幾個行人盡管未受傷,但是其周圍均被受傷行人占據,也將無法移動,疏散過程被迫中斷.

本節直觀地再現出密集型人群在不同的坡度條件下的疏散過程,以及不同程度的倒地現象,展現了密集型人群處于坡度人行設施中的安全隱患.接下來,引入兩兩行人成結隊的方式,作為減少倒地現象的安全措施.通過模擬數據得到倒地人數與坡度角大小、初始行人密度之間的函數關系,最終分析得出安全措施實施的最佳時機.

4 兩人結隊行走策略模擬

本節提出采用兩人結隊行走策略,作為引導行人安全疏散、減少倒地現象發生的方法.為了驗證此方法的有效性和可行性,下面將在模型中采用規則2.3.2,模擬兩人結隊行走策略的實施過程和最佳實施條件.為了便于比較,模型參數選用第3節中的設置,相應于規則2.3.1和2.3.2,將無安全措施的模型記為模型(I),考慮結隊行走措施的模型記為模型(II).

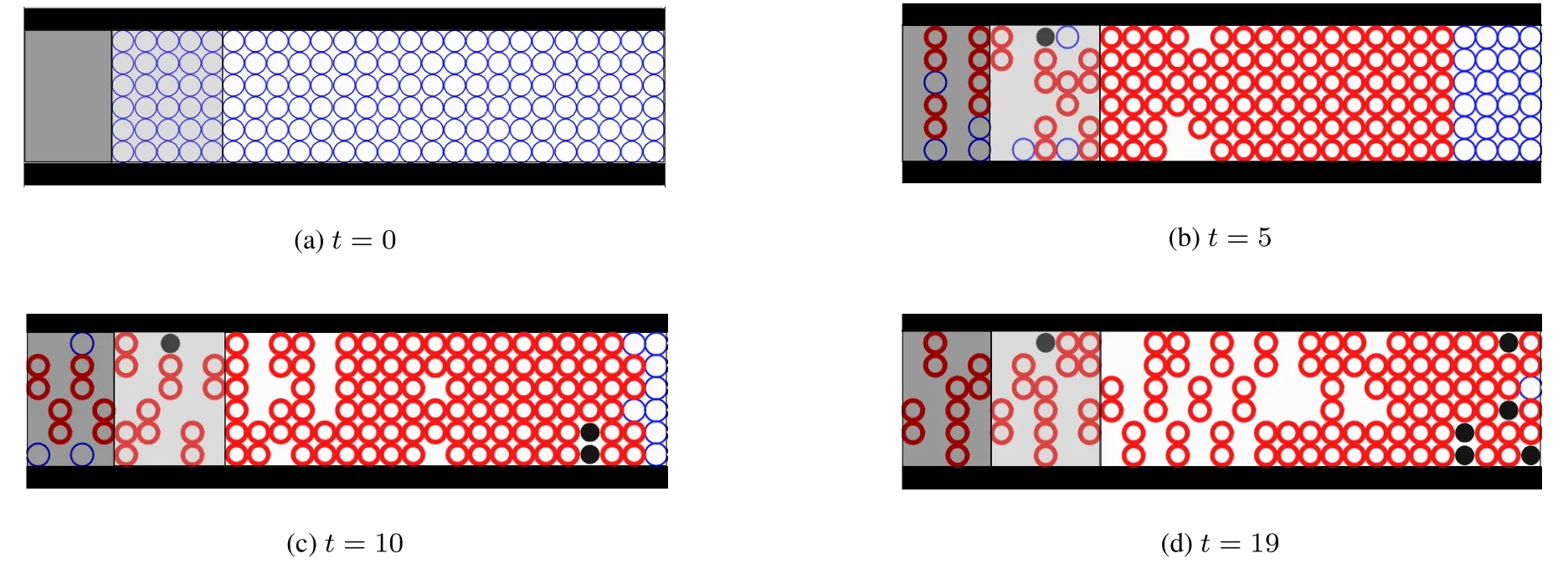
圖6 采用有安全措施規則2.3.2的模型模擬得到的行人疏散過程截圖(ρ0=1,θ=35°)Fig.6 Evacuation process simulated by the proposed model with safe rules 2.3.2(ρ0=1,θ=35°)

首先,直觀地驗證兩人結隊措施的可行性.采用模型(II),模擬得到的疏散過程截圖如圖6所示(拉伸在二維平面上).圖6所示結果均在ρ0=1,θ=35°,γ=0.8的條件下完成.此次模擬結果表明:人群在坡度角較大的設施中,當行人之間的推擠作用力達到單獨行人產生推力的80%(γ=0.8)時,行人便開始自行尋找鄰居行人結隊,增加自身抵抗擠壓作用力的強度,從而達到減少倒地危險的目的.比較模型(I)的模擬結果圖5與模型(II)的模擬結果圖6,在相同設施、相同初始密度條件下,圖6的結果表明本文所提的兩人結隊措施可以減少行人擠壓倒地現象的發生幾率,與規則2.3.2的理論分析相吻合.

其次,研究安全措施實施的最佳條件,并通過比較有無安全措施的模擬結果,定量地驗證兩兩結隊措施的可行性和有效性.為了找出高密度人群在不同的坡度設施條件下,行人承受的推力達到何值時采取結隊措施更為有效.下面研究在ρ0=1的情形下,坡θ,結隊參數γ以及倒地人數之間的變化關系,如圖7所示.該圖表明:當θ≤10°時,若γ≤0.5,盡管坡度角比較小,但是行人承受的擠壓力還沒有達到其倒地臨界值的一半,行人之間過早的采取兩兩結隊的措施,在這種情況下,每個小組行人作為一個整體前進,在密集型人群中,同時找到空目標位置的概率要比單個行人前進所需空目標位置的概率要小,導致行人流量減少,造成人群擁堵,從而增加了行人之間的擠壓作用,進一步引發少數行人不能忍受擠壓作用而倒地的現象;相反地,若取γ＞0.5,確保行人在無危險時,可獨自承受推擠作用,并正常前進,行人倒地現象發生的幾率將降低,此時的數據結果與圖4所示的圖像結果一致,即在坡度較小的情況下,行人正常行走不會發生倒地現象.當θ＞10°時,隨著坡度的增加,行人自身穩定性減弱,承受壓力的能力減弱,易被推倒.此時若盡早的采取兩兩結隊的安全措施可以有效地制止倒地現象的發生,此情況下取γ≤0.5,倒地人數明顯要少;相反地,若取γ＞0.5,表明沒有及時采取安全措施,倒地人數要比前者多.

從宏觀上觀察圖7的發展趨勢,隨著斜坡角度θ增大,以及結隊參數γ增大,倒地人數增多,換句話說,斜坡越陡,越早的采取結隊措施,可以有效減少倒地人數;斜坡越平坦,盡量使行人保持獨立行走,保證系統行人流量,可以減少密集人群疏散中的安全隱患.此外,圖7進一步表明,只要在行人承受的推擠作用力達到其自身的承受力之前采取兩兩結隊的安全措施,即可制止人群倒地現象中的“多米諾”效應,大幅度地減少行人倒地人數,即倒地人數小于15人,占系統總人數的10%以下,這與圖5(d)所示的倒地人數有明顯的差距.

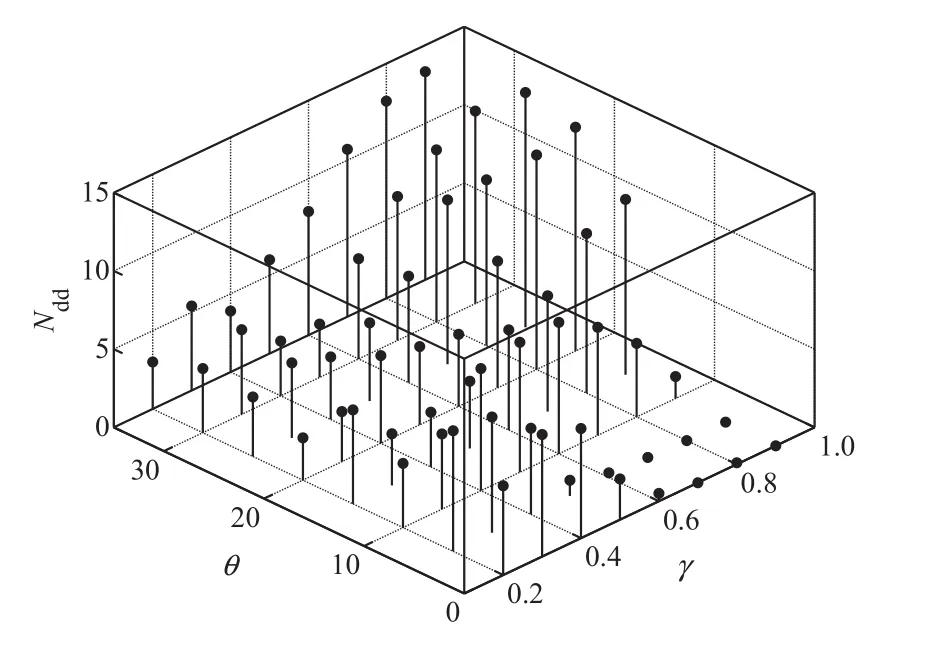
圖7 倒地人數(Ndd),斜坡角度(θ),結隊參數(γ)之間的關系.ρ0=1Fig.7 The relationship among the number of injured pedestrians(Ndd),the ramp angles(θ)and the parameters of using small groups(γ).ρ0=1

下面定量地分析產生倒地人數差距的原因.模擬中,分別采用模型(I)和模型(II),計算不同初始密度條件下,倒地人數隨坡度角變化而變化的函數關系,結果如圖8所示.

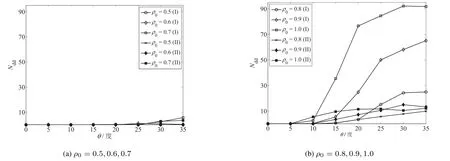
圖8 倒地人數(Ndd)與斜坡角度(θ)之間的關系Fig.8 The relationship between the number of injured pedestrians(Ndd)and the ramp angles(θ)

圖8(a)和圖8(b)分別表示初始密度介于0.5～ 0.7之間和0.8～ 1之間的倒地人數與坡度角之間的變化關系.這里模型(II)中結隊參數取為γ=0.8.圖8(a)表明初始密度ρ0≤0.7時,即總人數小于0.7(LA+LB)WA=105人,若θ≤20°,兩種模型的倒地人數為0;若θ≥25°,初始密度ρ0≤0.6時,倒地人數亦接近于0,ρ0=0.7時,出現少數人倒地現象;而且隨著坡度增加,倒地人數也有一定增加,但是不超過10人,小于此時系統最大人數的10%.兩模型的變化趨勢接近一致,隨著初始密度增大,坡度增大,行人倒地現象出現.相對圖8(a)而言,圖8(b)表明在初始密度ρ0≥0.8時,兩個模型變化趨勢較明顯:每條曲線表明,初始密度固定的條件下,倒地人數是坡度的增函數;當坡度取定,高密度曲線位于低密度曲線上方,暗含倒地人數是初始密度的增函數.另外,取定同一初始密度,將模型(I)和模型(II)相應的曲線作比較,取定ρ0=0.8,當θ≤20°時,模型(I)和模型(II)的倒地人數均小于5,兩模型的曲線重合,而θ＞20°時,模型(I)的倒地人數接近于(II)的2倍;當ρ=0.9,θ≥15°,或ρ=1,θ≥10°時,受到“多米諾”效應的影響,無安全措施的模型(I)再現的倒地人數急劇增加,最高可達系統人數的約90/150=60%,而采取兩兩結隊安全措施的模型(II)模擬得到的倒地人數始終保持在系統人數的10%以下.

總之,此節模擬結果合理地驗證了兩兩結隊方式在減少倒地現象以及制止人群推擠中的“多米諾”效應的可行性和有效性,為進一步將兩兩結隊方式應用于指導實際人群安全疏散奠定理論基礎.

5 結束語

本文建立了一種勢函數場元胞自動機模型,同時考慮行人之間相互擠壓作用力場與受行人設施坡度影響的勢函數場.利用所提模型模擬人群在進入具有坡度人行設施時的擠壓倒地現象,分析斜坡角度、人群初始密度與行人擠壓倒地現象之間的作用機制;并在模擬現象基礎上,將行人兩兩結伴行走的機制引入模型,作為減少行人倒地現象發生的安全疏散策略,并通過模擬驗證該疏散策略的可行性和有效性,定量地分析不同初始密度或不同坡度條件下,安全措施實行的最佳條件.

盡管本文研究的場景為三維空間上的坡度人行設施,但是將行人垂直投影在每個子區域上,在每個子區域上可將行人運動視為二維問題,忽略了行人的立體結構,但并不影響模型描述行人運動現象.為了可以更加直觀模擬實際行人運動,將來的研究工作一方面將直接考慮三維空間中行人的運動特征,并展示三維空間中的行人運動過程,達到所見即所得的模擬效果,而不做行人投影和行走區域拉伸等空間降維處理;另一方面擴展所提模型的可模擬范圍,如將模擬應用于模擬同時具有坡度和轉角的復雜人行設施中的人群疏散過程,考慮行人可視度受到外界照明條件影響下的人群疏散過程,分析不同場景中疏散問題的安全隱患,并提出可行的安全疏散方法,最終在大量理論研究基礎之上,將安全疏散方法應用于解決實際問題.

[1]Helbing D,Molnˊar P.Social force model for pedestrian dynamics.Physical Review E,1995,51(5):4282–4286.

[2]Helbing D,Buzna L,Johansson A,et al.Self-organized pedestrian crowd dynamics:Experiments,simulations,and design solutions. Transportation Science,2005,39(1):1–24.

[3]陳 鋒,翟慶生,王子甲.社會力行人仿真模型的分子動力學方法實現.系統工程理論與實踐,2014,34(4):1003–1010. Chen F,Zhai Q S,Wang Z J.Implementation of social force pedestrian simulation model by molecular dynamic method.Systems Engineering:Theory&Practice,2014,34(4):1003–1010.(in Chinese)

[4]Hughes R L.A continuum theory for the fow of pedestrians.Transportation Research:Part B,2002,36(6):507–535.

[5]Huang L,Wong S C,Zhang M P,et al.Revisiting Hughes’dynamic continuum model for pedestrian fow and the development of an effcient solution algorithm.Transportation Research:Part B,2009,43(1):127–141.

[6]Xiong T,Zhang P,Wong S C,et al.A macroscopic approach to the lane formation phenomenon in pedestrian counterfow.Chinese Physics Letters,2011,28(10):1–4.

[7]Blue V J,Embrechts M J,Adler J L.Cellular automata modeling of pedestrian movements//Proceeding of IEEE Conference on Systems,Man,and Cybernetics.Orlando:IEEE Press,1997,3:2320–2323.

[8]Burstedde C,Klauck K,Schadschneider A,et al.Simulation of pedestrian dynamics using a two-dimensional cellular automaton. Physica A,2001,295(3/4):507–525.

[9]Kretz T.Pedestrian traffc:On the quickest path.Journal of Statistical Mechanics:Theory and Experiment,2009(3):1–26.

[10]Kirik E,Yurgel’yan T,Krouglov D.Artifcial intelligence of virtual people in CA FF pedestrian dynamics model//Wyrzykowski R, Dongarra J,Karczewski K,et al.Lecture Notes in Computer Science.Berlin Heidelberg:Springer-Verlag,2010,513–520.

[11]Huang H J,Guo R Y.Static foor feld and exit choice for pedestrian evacuation in rooms with internal obstacles and multiple exits. Physical Review E,2008,78(2):1–6.

[12]Guo R Y,Tang T Q.A simulation model for pedestrian fow through walkways with corners.Simulation Modelling Practice and Theory,2012,21(1):103–113.

[13]JianXX,WongSC,ZhangP,etal.Perceivedcostpotentialfeldcellularautomatamodelwithanaggregatedforcefeldforpedestrian dynamics.Transportation Research:Part C,2014,42:200–210.

[14]趙宜賓,黃 猛,張鶴翔.基于元胞自動機的多出口人員疏散模型的研究.系統工程學報,2012,27(4):439–445. Zhao Y B,Huang M,Zhang H X.On multi-exit occupant evacuation model based on cellular automaton.Journal of Systems Engineering,2012,27(4):439–445.(in Chinese)

[15]陳 然,李 翔,董力耘.地鐵站內交織行人流的簡化模型和數值模擬.物理學報,2012,61(14):1–9. Chen R,Li X,Dong L Y.Modeling and simulation of weaving pedestrian fow in subway stations.Acta Physica Sinica,2012,61(14): 1–9.(in Chinese)

[16]Jian X X,Zhang X N.Potential feld cellular automata model for pedestrian evacuation in a domain with a ramp.Mathematical Problems in Engineering,2014(2014):1–7.

[17]Yang L Z,Li J,Liu S B.Simulation of pedestrian counter-fow with right-moving preference.Physica A,2008,387(13):3281–3289.

[18]Kuang H,LI X L,Wei Y F,et al.Effect of following strength on pedestrian counter fow.Chinese Physics B,2010,19(7):1–9.

[19]Guo R Y,Huang H J,Wong S C.Route choice in pedestrian evacuation under conditions of good and zero visibility:Experimental and simulation results.Transportation Research:Part B,2012,46(6):669–686.

[20]周金旺,鄺 華,劉慕仁,等.成對行為對行人疏散動力學的影響研究.物理學報,2009,58(5):3001–3007. Zhou J W,Kuang H,Liu M R,et al.Paired behavior effect on pedestrian evacuation dynamics.Acta Physica Sinica,2009,58(5): 3001–3007.(in Chinese)

[21]任 剛,丁晨滋,陸麗麗,等.基于元胞自動機的結伴過街行人流建模與仿真.交通運輸系統工程與信息,2014,14(2):45–50. Ren G,Ding C Z,Lu L L,et al.Model and Simulation of group pedestrian fow on a crosswalk based on cellular automaton.Journal of Transportation Systems Engineering and Information Technology,2014,14(2):45–50.(in Chinese)

[22]宋衛國,于彥飛,范維澄,等.一種考慮摩擦與排斥的人員疏散元胞自動機模型.中國科學:E輯,2005,35(7):725–736. Song W G,Yu Y F,Fan W C,et al.A cellular automata evacuation model considering friction and repulsion.Science in China:E Edition,Engineering&Materials Science,2005,35(7):725–736.(in Chinese)

[23]Zhang P,Jian X X,Wong S C,et al.Potential feld cellular automata model for pedestrian fow.Physical Review E,2012(85):1–8. [24]Moussa¨?d M,Perozo N,Garnier S,et al.The Walking behaviour of pedestrian social groups and its impact on crowd dynamics.PLoS ONE,2010,5(4):1–7.

[25]Schadschneider A,Klingsch W,Kl¨upfel H,et al.Evacuation dynamics:Empirical results,modeling and applications//Meyers R A. Extreme Environmental Events:Complexity in Forecasting and Early Warning.Berlin,Heidelberg:Springer-Verlag,2011,517–550. [26]Kirchner A,Kl¨upfel H,Nishinari K,et al.Discretization effects and the infuence of walking speed in cellular automata models for pedestrian dynamics.Journal of Statistical Mechanics:Theory and Experiment,2004,2004(10):1–21.

[27]Jiang Y Q,Zhang P,Wong S C,et al.A higher-order macroscopic model for pedestrian fows.Physica A,2010,389(21):4623–4635. [28]Zhao H K.A fast sweeping method for Eikonal equations.Mathematics of Computation,2005,74(250):603–627.

[29]Fruin J.The causes and prevention of crowd disasters//Smith R A,Dickie J F.Engineering for Crowd Safety.Amsterdam:Elsevier, 1993:99–108.

Dense crowd grouping evacuation strategy based on potential feld model

Jian Xiaoxia,Zhang Xiaoning*
(School of Economics and Management,Tongji University,Shanghai 200092,China)

A potential feld cellular automata model is proposed to reproduce the pushing down phenomena for crowd evacuation.In this model,the moving direction of the crowd on a domain with a ramp is navigated by combing a pushing force feld within a cost potential feld.In addition,the proposed model is employed to analyze the interaction among the ramp angle,the crowd initial density and the pushing down phenomena. The analysis shows that the two-people-together strategy may decrease the number of pedestrians falling to the ground,and the simulation shows that the percentage is only less than 10%of the pedestrians.

potential feld;cellular automata model;pushing;pushing down;two-people-together;ramp

U491

A

1000-5781(2016)06-0850-13

10.13383/j.cnki.jse.2016.06.013

菅肖霞(1981–),女,內蒙古包頭人,博士,博士后,研究方向:行人交通建模與管理,Email:jianxiaoxia_2000@163.com;

2014-10-09;

2015-03-02.

國家自然科學基金資助項目(71531011;71401126;71125004);中國博士后科學基金資助項目(2014M551460;2015-T80457);中央高校基本科研業務費專項資金資助(10247201601164).

*通信作者

張小寧(1975–),男,安徽省安慶人,博士,研究員,教授,研究方向:交通優化與管理,Email:cexzhang@tongji.edu.cn.